基于振动法的拉索索力测试研究

2021-11-05况中华

建筑施工 2021年7期

况中华

上海建工集团股份有限公司上海 200080

拉索是一种只受拉不受压的非线性结构，因其高效的受拉性能，被广泛用于大跨度斜拉桥、拱桥、穹顶、屋盖网架、空间索网等特殊复杂结构。拉索是索结构的关键受力构件，通过自身索体预应力的大小实现整体索结构内力分布、保证结构稳定性、传递结构荷载、控制结构线形形态等。因此，无论在索结构施工过程阶段还是运营使用阶段，准确地测量以及控制拉索的索力大小对索结构的整体安全性和稳定性都至关重要。

目前，常用的拉索索力测量方法主要包括压力传感器测试法、磁通量法和振动法。压力传感器测试法：通过在拉索锚固端设置压力传感器，将压力传感器所测压力作为拉索的索力。该方法需在建造过程中事先将压力传感器安装至拉索锚固端，无法测量已有索结构的拉索索力。磁通量法：在拉索索体上安装电磁传感器，通过拉索受拉后索体横截面积变化引起的磁通量变化来推算拉索的索力。该方法同样需事先安装磁通量传感器，仅适用于在建索结构的拉索索力测量。振动法：首先利用加速度传感器釆集测量拉索在环境激励或人工激励下的自振频率，然后通过自振频率与索力的关系计算拉索索力。该方法可适用于在建和已建的索结构，应用范围较广，但该方法的测量精度受理论公式的准确性以及拉索边界条件的影响[1-2]。

以往采用振动法测量拉索索力时，为便于计算，往往将拉索简化为两端铰支的振弦，忽略拉索边界刚度对索力的影响，无法保证索力测量结果的准确性。本文在考虑拉索锚固边界及减振器的边界刚度影响的情况下，进行拉索的有限元仿真分析，拟合出拉索索力与多阶固有频率之间的理论公式，再将实测多阶固有频率代入理论公式计算拉索的真实索力，从而提高振动法测量拉索索力的准确性。

1 拉索的梁振动模型

梁振动模型是经典的拉索振动模型，是将拉索振动模拟为考虑轴力作用的梁振动，只考虑拉索的横向振动，忽略拉索的轴向振动。梁振动模型的优点是可以考虑拉索抗弯刚度对振动的影响，即假定拉索在轴力（索力T）作用下作横向振动时，考虑轴力因拉索变形而产生的弯矩作用（图1）。

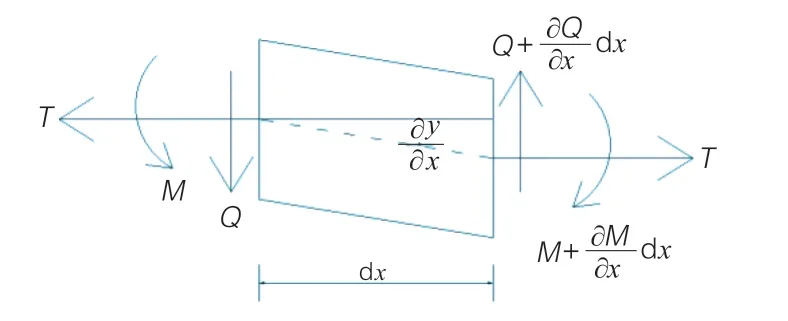
图1 梁振动模型受力示意

依据梁的动力学状态，可建立运动微分方程，如式（1）所示。

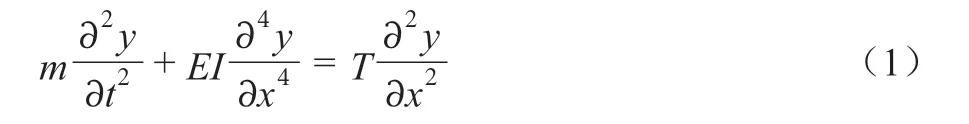
假定拉索振动为正弦振动，可设拉索的位移函数y＝φ(x)·sin(ωt＋φ)，代入上式可得式（2）：

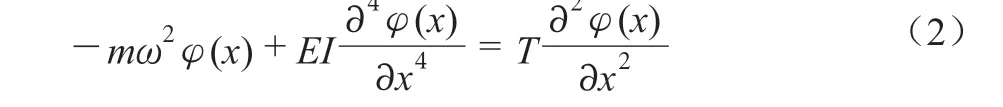
设 α2＝T/(EI)，β4＝mω2/(EI)，代入上式可得式（3）：

设式（3）的解为：

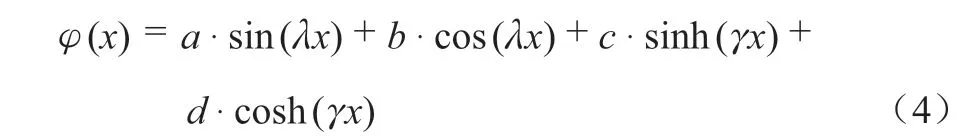
式中：

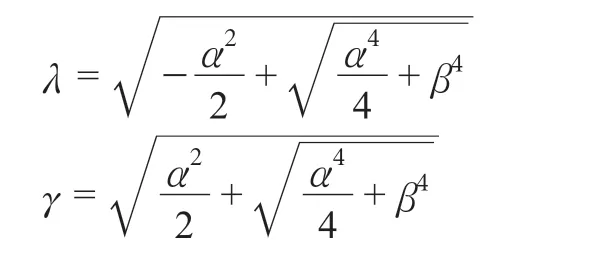
当拉索为两端铰支时，由两端位移为0，弯矩为0的约束条件可解出索力的解析解，如式（5）～式（7）所示。

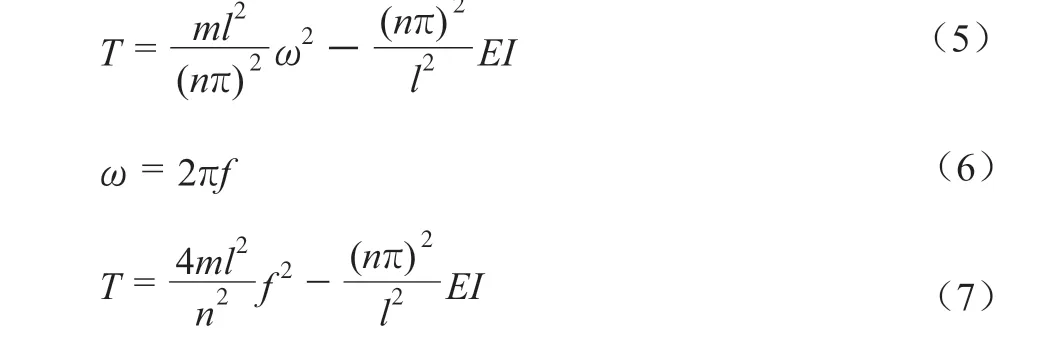
式中：ω——拉索振动的圆频率；

f ——拉索振动频率；

m ——拉索的单位长度质量。

通过上述拉索索力计算公式可得，拉索索力基本与固有频率呈二次函数关系。当拉索两端边界为铰支时，可得出拉索索力与频率间的解析关系式，而当拉索两端为弹性边界时则无法得出解析式，须通过数值仿真获取数值解。

2 拉索的有限元振动模型

依据上述拉索的梁振动模型的解析式可知，拉索的振动特性与拉索边界刚度有着密切关系，但是仅在拉索锚固边界为铰支的情况下，才能通过拉索的梁振动模型计算得出解析解，而且计算过程相对复杂。同时，上述拉索的梁振动模型忽略了几何刚度的影响，无法真实反映拉索在索力作用下的刚度变化，从而影响计算结果的准确性。

针对拉索的梁振动模型在解析过程中存在的各种问题，本文选取目前较为主流的有限元数值分析法建立拉索的振动模型，在拉索的梁振动模型基础上考虑拉索结构的几何刚度效应以及拉索锚固边界和减振器的刚度，尽可能真实地反映拉索的振动状态。

2.1 锚固边界刚度

建立拉索的有限元振动模型时，基于梁振动模型理论采用梁单元模拟拉索，但是梁单元具备可受拉、受压、受弯和受扭的单元属性，与拉索的近似只受拉不受压非线性属性有所差别。因此，在模拟时还应考虑P-Δ效应，考虑内力对梁单元几何刚度的影响。

梁单元节点具备6个自由度：三向线位移（x，y，z）和三向角位移（Rx，Ry，Rz）。拉索以平面振动为主，模拟时可忽略拉索锚固端扭转刚度的影响。因此，建立模型时依据拉索实际边界情况，在梁单元两端节点的4个自由度上（y，z，Ry，Rz）施加弹性约束，约束节点的扭转自由度（Rx），以此反映边界刚度对拉索振动模态的影响；梁单元轴向（x）施加内力（索力），以此模拟拉索的索力对几何刚度的影响（图2）。

图2 考虑锚固边界刚度的拉索有限元振动模型

拉索锚固边界刚度K的获取，首先是通过建立索结构的整体有限元模型；然后在整体有限元模型中删除所需要分析的拉索单元，并在拉索单元锚固节点上分别施加5个自由度方向的单位力，通过计算各个自由度方向单位力作用下的变形Δ；最后，可得出拉索锚固端各个自由度所对应的边界刚度K＝1/Δ。

2.2 减振器的模拟

拉索为柔性结构，在诸如车辆荷载、风荷载等活载作用下易产生振动，尤其是大跨度斜拉桥上的拉索易在风雨的作用下产生共振，从而影响整体结构的安全性和稳定性。因此，为了避免拉索在外界作用下产生共振或因振动导致被破坏等情况，常常在拉索锚固端附近设置减振器，起到减小振幅甚至抑制振动的效果。

减振器的介入会改变拉索的振动体系，无论是减振器的约束刚度、阻尼还是安装位置都会影响拉索振动的固有频率以及振型。若要精确计算带减振器的拉索的固有频率，则必须准确模拟减振器对拉索振动体系的影响。本文依据减振器的构造形式、材料弹性模量来推算减振器的约束刚度Kj，并在拉索对应位置施加相对应约束刚度的弹性约束，从而实现模拟减振器对拉索振动影响的效果。

因减振器的一端与拉索连接，另一端与索网整体结构相连，在建立带减振器的拉索有限元振动模型时，不能仅将减振器约束刚度作为弹性约束的刚度，而应将减振器约束刚度Kj和索网整体结构刚度K(y,z)这二者的串联刚度作为弹性约束的刚度，施加于拉索有限元振动模型中（图3）。

图3 考虑减振器刚度的拉索有限元振动模型

减振器与索网整体结构的串联刚度Kc可按式（8）、式（9）计算。

式中：Kj——减振器约束刚度；

K(y,z)——索网整体结构刚度；

Kc——串联刚度。

2.3 固有频率与索力的关系

考虑拉索锚固端边界以及减振器约束边界的作用，将拉索索力作为初始内力施加于拉索轴线方向，在考虑P-Δ效应的情况下计算拉索振动的固有频率。通过计算不同索力作用下的拉索固有频率，拟合出频率-索力的理论公式，从而可将实测拉索振动频率代入此理论公式计算出拉索实测索力。一般选取5～10组索力计算对应拉索固有频率，通过多组索力和对应的固有频率进行频率-索力的函数关系拟合。参照上文中拉索的梁振动模型，可知拉索索力与频率基本呈二次函数关系。因此，可利用二次函数关系式进行频率-索力的理论公式拟合（图4）。

图4 拉索的频率-索力拟合曲线

3 现场测试采样

振动法测量拉索索力的关键是获取拉索的固有频率，现场测量主要是通过在拉索上固定加速度传感器，获取拉索的加速度时程信号，并通过FFT转换得到拉索的固有频率。但在现场实际测量过程中，外界环境的白噪声干扰不可避免，因此，为了确保测量所得固有频率的准确性以及测量结果的可靠性，应对每一根拉索进行多次测量，而且每次测量的采样频率应不相同，以此获取拉索的多阶固有频率。依据测量获取的多阶固有频率可换算得出多个拉索索力计算结果，以多个拉索索力计算结果的平均值作为可靠的索力测量值。拉索的横向振动可分为y、z这2个方向的振动（图5），且根据不同方向的约束边界条件，同一阶次的2个方向振型也会有所不同。因此，在现场测量之前，应依据拉索的理论振型确定加速度传感器的固定方向，获取指定方向的固有频率。与此同时，拉索的振动具有周期性特点，现场测量主要通过采集某个周期性振动过程中的多个数据点来反映该振动的周期性特征，从而计算出该振动的固有频率。在计算过程中，要较为准确地拟合出一条周期性时程曲线至少需要5个数据点，因此，为了保证所采集的固有频率的准确性，测量时的采样频率至少为固有频率的5倍（图6）。

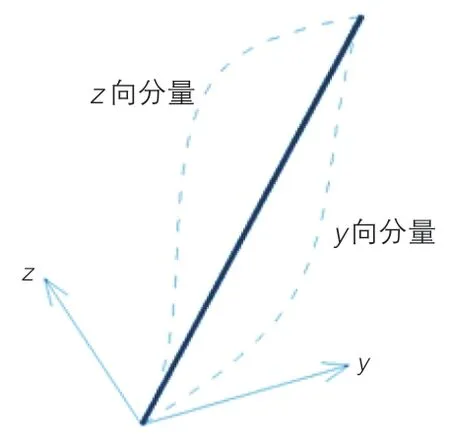
图5 拉索振型示意

图6 拉索的加速度时程曲线

4 案例分析

本文以一大跨度系杆拱桥为例，验证上述振动法测量拉索索力的准确性和可靠性。该项目为下承式系杆钢拱桥（图7），主桥跨径109 m，全桥共设2片箱形拱肋和系梁，系梁之间通过工字型钢横梁连接。全桥对称设置15组拉索，拉索间距6.5 m，拉索上锚点采用耳板与拱肋插销连接，拉索下锚点通过锚具与系梁固定连接，在距离下锚点1.95 m位置设置高阻尼橡胶减振器（图8）。

图7 下承式系杆钢拱桥立面示意

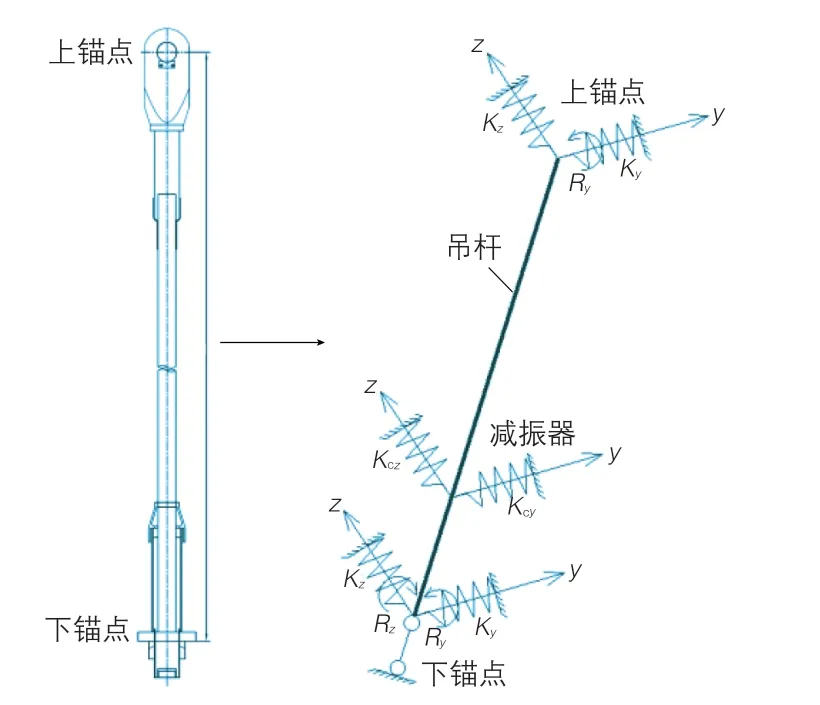
图8 拉索边界示意

在进行拉索索力测量前，先通过有限元仿真分析确定每根拉索在15组不同索力（100～1 000 kN）下的前3阶固有频率，再通过二次函数关系式拟合出每根拉索的频率-索力理论公式。现场测量时选取10倍固有频率的采样频率进行测试采样，以确保实测固有频率的准确性。最后，将实测固有频率代入频率-索力理论公式中计算每根拉索的索力实测值。通过计算得出15组拉索的频率-索力理论公式T＝af2＋bf＋c，如表1所示。

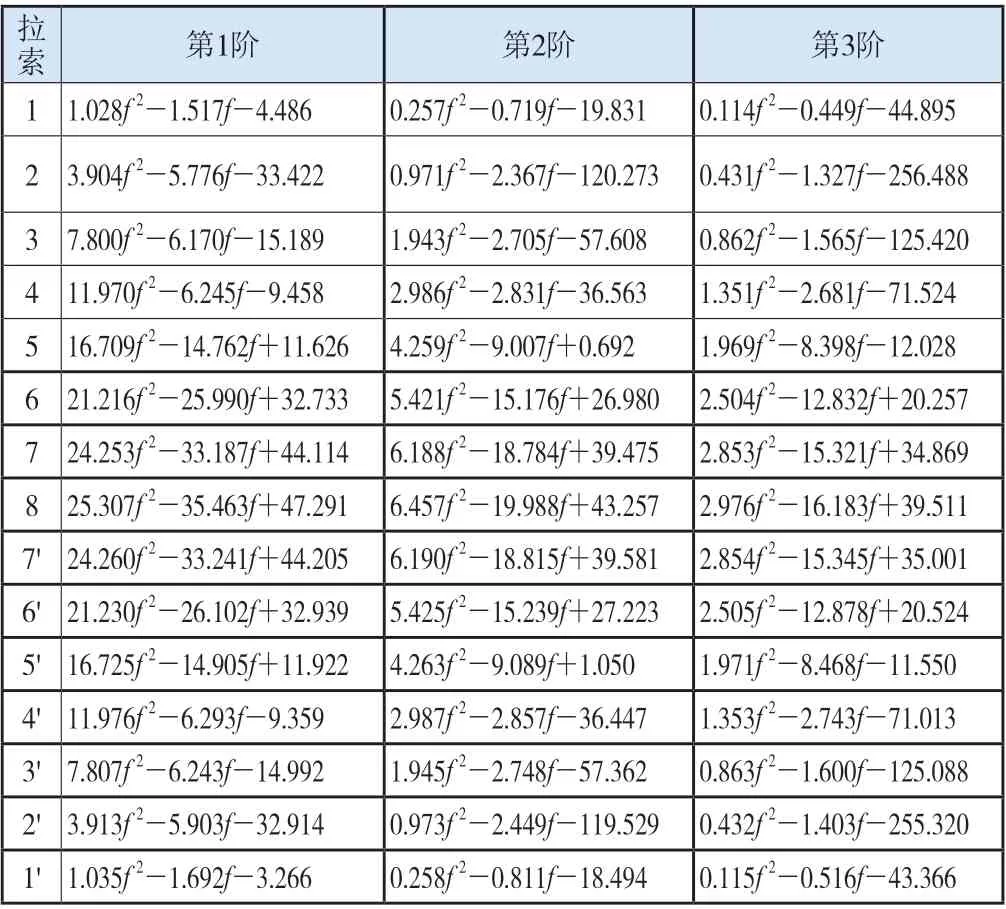
表1 拉索的频率-索力理论公式

将每根拉索的3阶实测频率代入上述频率-索力理论公式，计算得出每根拉索的3阶索力平均值，如表2所示。通过拉索索力的实测值与理论值对比可得，除1、2号拉索索力实测值与理论值的偏差率为10%外，其余拉索索力实测值与理论值的偏差基本在8%以内，表明本文所述拉索索力的振动法测量准确性可满足工程需求，且通过3阶固有频率换算的索力实测平均值的可靠性相对较高。

表2 拉索索力实测值-理论值对比

5 结语

本文对振动法测量拉索索力进行了研究，在考虑拉索锚固边界刚度以及减振器边界刚度对拉索振动固有频率影响的情况下，建立了拉索的梁振动模型，并通过有限元仿真分析计算拉索在多组索力作用下的多阶固有频率，再利用二次函数关系式拟合出拉索的频率-索力理论公式，最终将实测拉索多阶固有频率代入频率-索力理论公式中，计算拉索多阶索力的平均值作为索力测量值。

通过实际工程案例的验证，本文提出的有限元分析结合实测多阶频率的拉索索力测量方法，可提高振动法测量索力的准确性和可靠性。