复杂随形拱壳混凝土结构施工过程模拟与方案优化

2021-11-05何湘锋陈学英喻泽成

建筑施工 2021年7期

关键词：支撑体系轴力内力

何湘锋陈学英喻泽成余波

1. 中国建筑第二工程局有限公司广西南宁 530012；2. 广西大学土木建筑工程学院广西南宁 530004

1 工程概况

该项目为板式高层建筑，呈“山”字形，主立面为南北朝向，效果图如图1所示。

图1 项目效果图

为营造山水的意境，设计师在建筑立面设计多个大开洞[1-2]，各洞口均为钢筋混凝土随形拱壳结构，且造型独特、形状各异。其中，B2拱壳结构建筑高度最高，孔洞面积最大，其立面和俯视图如图2所示。

图2 B2随形拱壳结构立面及俯视示意

独特的造型给施工方案设计带来了以下技术难题：

1）B2拱壳的建筑高度为70 m，最大跨距为30 m，对模板支撑体系的设计技术要求较高。

2）B2拱壳造型不规则，空间受力复杂，拱壳结构从右侧4层开始，如下小上大的花瓶壁向外凸出，拱壳南北侧设计成流线型喇叭口状，拱顶合拢前最大悬臂达12 m，所以在拱壳结构成形前需要关注施工阶段的受力情况，并且考虑内力变形的累积影响。

3）拱形变化部分与竖向结构交叉多，拱顶部类似于框支结构，结构自重荷载较大，从而导致施工阶段结构内力响应明显。

4）施工周期长，在施工过程中部分完成的结构与临时支撑系统所构成的结构的形状和材料性质都是随时间不断变化的[3]，所以需要考虑施工过程中混凝土结构的时变效应，建立合理准确的计算模型。

5）施工工序复杂，根据逐层施工过程，拱顶合拢前最大悬臂达12 m，合拢时拱顶分环逐层合拢成形，受力及其转换过程复杂，可能导致结构的最不利工况（应力、变形）出现在施工阶段，而不是正常使用阶段[4]。由此可见，有必要进行施工阶段全过程受力分析并根据分析结果确定安全合理的施工方案。

2 随形拱壳混凝土结构施工过程模拟

为准确模拟B2拱壳施工过程结构、边界和荷载的情况，本文采用有限元软件MIDAS FEA对拱壳结构建立空间有限元模型，以模拟拱壳结构在施工过程中的受力状态。

2.1 模型假定与单元选择

随形拱壳为三维异形空间结构，结构复杂，受力具有非对称性，拱壳及其相连的梁、墙肢和模板支撑体系之间有共同作用。为准确地分析拱壳施工过程的受力状态，提高计算效率，分析模型采取以下简化和假定：

1）仅对B2拱壳结构及与其直接相连的墙肢和楼板梁进行建模分析。

2）因拱壳结构两侧的框架结构整体刚度大，故将与拱壳相连的楼板梁远端假定为固定端约束。

3）楼面荷载等效成均布荷载作用在与拱壳相连的梁和墙肢上。

4）拱壳底部的模板支撑体系采用只受压弹簧单元进行模拟。

拱壳结构三维有限元模型如图3所示。分析模型中，壳体单元和拱壳上竖向墙肢采用空间壳单元模拟，与拱壳上水平相连的楼板梁采用空间梁单元模拟，模板支撑体系等效成只受压弹簧单元模拟。同时，分析模型考虑了拱壳与竖向墙肢、水平梁体的连接关系，以确保竖向墙肢和水平梁的荷载向拱壳结构传递。

图3 B2随形拱壳有限元模型

考虑到拱壳结构逐层施工的实际情况，分析模型也随施工过程逐层进行单元划分，共划分35 622个单元，拱壳模型、壳体与相连梁体连接模型、壳体与竖向墙肢连接模型分别如图4～图6所示。

图4 B2随形拱壳结构模型

图5 B2随形拱壳与楼板梁连接模型

图6 B2随形拱壳与竖向墙肢连接模型

2.2 荷载及边界条件

随形拱壳体在施工过程中承受的荷载包括壳体结构自重荷载、壳体上相连的楼板梁、竖向墙肢的自重荷载和施工活荷载等。施工活荷载包括支撑体系、施工操作人员和施工机械的质量，根据规范[5-6]规定，活荷载取均布荷载3.0 kN/m2，荷载组合按照1.3×恒载＋1.5×活载进行计算。

结合拱壳施工过程中的实际情况，拱壳底部固结模拟刚性基础连接，与拱壳相连的楼板梁远端固结，拱壳下表面采用只受压弹簧连接单元模拟模板支撑体系，弹簧单元刚度取为106 kN/m3，边界条件模拟如图7～图9所示。

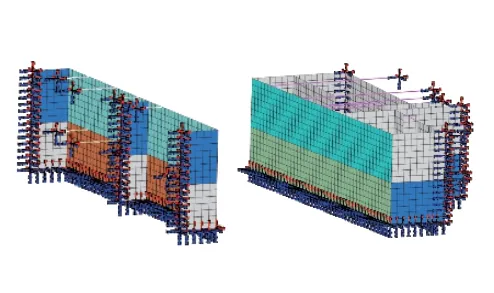
图7 拱壳底部边界条件模拟

图8 梁端边界条件模拟

图9 拱壳与模板支撑体系连接的模拟

2.3 施工过程模拟

结构的施工过程分析为非线性分析过程，结构形式、边界条件、荷载和材料特性将随施工过程发生变化。本文采用有限元软件MIDAS FEA的施工阶段分析模块，应用“激活”与“钝化”功能。对单元、荷载及边界条件等进行“激活”操作，使相应激活单元的质量刚度、荷载及边界条件参与到有限元分析过程中。相反地，“钝化”操作是使相应的单元、荷载及边界退出有限元模型的计算。因此，通过对分析模型单元、荷载及边界条件的激活与钝化可以有效地模拟拱壳结构的施工过程。此外，为考虑混凝土材料的时间依存特性，通过定义单元龄期和施工阶段持续时间定义混凝土抗压强度的变化、徐变、收缩等[7]。

3 随形拱壳混凝土结构施工方案优化

随形拱壳采用逐层拱壳及其相连楼板梁、竖向墙肢同时施工的方案，其模板支撑体系和拱壳结构施工过程的安全性是整个施工方案关键内容。为此，本文结合拱壳施工过程模拟，对施工过程模板支撑体系和拱壳结构的受力情况进行分析，并借此为模板支撑体系的设计提供依据，并对施工方案进行优化。

3.1 随形拱壳模板支撑体系拆卸方案优化

不同的模板支撑体系拆卸方案会对模板支撑体系和拱壳结构的受力产生影响，合理的模板拆卸方案可以为模板支撑体系的设计提供依据[8]。由于B2随形拱壳结构从F12开始向外侧悬挑，逐层施工阶段分析中重点考虑F12～F21共10个阶段的受力分析。

如表1所示，根据不同的模板拆卸方案，可知混凝土浇筑过程中方案一为全部楼层模板支撑状态，方案二结构为单层模板支撑状态，方案三为三层模板支撑受力状态，方案四为三层和多层支撑受力状态。

表1 模板支撑体系拆卸方案

通过对上述4个方案进行施工过程模拟分析，各楼层模板支撑体系承受的设计荷载如图10所示。由图10可知，上述4个方案的模板支撑设计荷载值最不利工况均出现在F18～F21之间，其主要原因是拱壳顶部楼层水平投影面积大，上部结构的自重荷载由壳壁直接传递给了模板支撑。同时，方案一模板支撑计算值最不利工况出现在F18，此时最大设计荷载值为49.57 kN/m2；方案二模板支撑计算值最不利工况出现在F21，此时最大设计荷载值为48.56 kN/m2，比方案一减小2.04%，基本维持不变；方案三模板支撑计算值最不利工况出现在F19，此时最大设计荷载值为67.96 kN/m2，比方案一增大37.10%；方案四模板支撑计算值最不利工况出现在F18，此时最大设计荷载值为49.91 kN/m2，比方案一增大0.69%，基本维持不变。

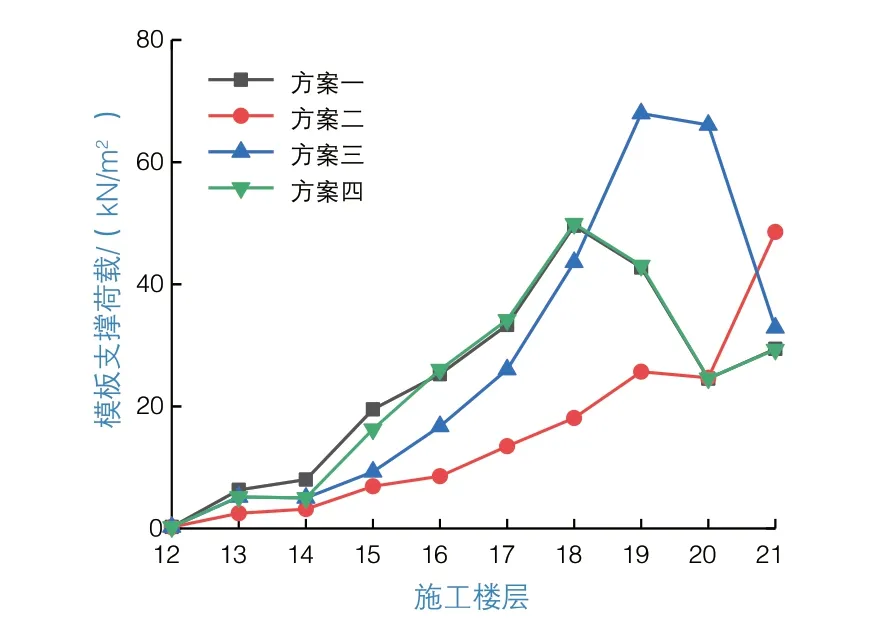
图10 不同方案的模板支撑荷载对比

进一步分析上述各个方案在整个施工阶段内拱壳结构最大轴力和弯矩值，计算结果如图11、图12所示。由图可知，随着施工楼层增加，拱壳结构单位宽度最大轴力和弯矩逐渐增大，施工到F21时均达到最大值。由图11可知，4个方案拱壳结构的轴力值相差甚小，其中方案四的拱壳结构单位宽度最大轴力值最大，为1 886.16 kN/m，方案一的拱壳结构单位宽度最大轴力值最小，为1 789.64 kN/m，两者的变化幅值在5%以内；由图12可知，在施工楼层F12～F17之间，4个方案的正负弯矩值吻合程度较高，在施工完F17后，弯矩值开始出现较大偏差，其正负弯矩绝对值按从大到小排序为：方案二＞方案三＞方案四＞方案一，其中方案二的拱壳结构单位宽度最大正负弯矩绝对值分别为91.60 kN·m/m和123.22 kN·m/m，比方案一增大16.41%和21.24%；方案三的拱壳结构单位宽度最大正负弯矩绝对值分别为89.11 kN·m/m和116.14 kN·m/m，比方案一增大13.24%和14.28%；方案四的拱壳结构单位宽度最大正负弯矩绝对值分别为81.24 kN·m/m和104.47 kN·m/m，比方案一增大3.24%和2.79%，变化幅度很小。

图11 不同方案的拱壳结构最大轴力对比

图12 不同方案的拱壳结构最大弯矩对比

为研究不同模板拆卸方案对成拱后拱壳结构内力的影响，分别对4种模板拆卸方案下拱壳结构最终内力值进行统计，并与不考虑施工阶段分析的拱壳内力值进行对比，结果见表2。

表2 模板拆卸施工方案对拱壳成形受力的影响

由表2可知，不考虑施工阶段分析，拱壳结构的轴力和弯矩计算值偏小，与施工阶段分析相比，最大偏差为8.48%和20.61%，可见不考虑施工阶段分析会低估拱壳结构的内力水平。综上所述，采用方案二浇筑混凝土时只有单层模板支撑能最大化减小模板支撑计算荷载值，但下层拱壳结构受力明显变大，同时由于拆卸模板需遵循混凝土龄期达到28 d设计强度的规定，故总工期不满足预期施工进度安排的要求；采用方案三模板支撑计算荷载值最大，后续进一步优化难度较大；方案一和方案四计算结果较接近，表明拆卸F12～F14模板对结构受力无大影响，故选择方案四作为最优方案。

3.2 随形拱壳F17～F21上部结构施工方案优化

3.1节对模板支撑体系拆卸方式进行优化，但分析结果表明模板支撑体系设计荷载值仍处于较高水平，超出模板支撑体系的极限荷载值。

为保证施工过程模板支撑体的安全，考虑拱壳F17～F21的上部结构的自重较大，现拟对拱壳F17～F21的上部结构进行施工顺序优化，以减小拱壳上部结构荷载对模板支撑体系的影响。以3.1节的方案四为基础，拟提出的拱壳F17～F21上部结构施工方案如表3所示。

表3 拱壳F17～F21上部结构的施工方案

对上述方案进行施工过程模拟分析，模板支撑体系设计荷载值见图13，拱壳结构的内力见图14、图15。

图13 不同施工方案的模板支撑荷载对比

图14 不同方案的拱壳结构最大轴力对比

图15 不同方案的拱壳结构最大弯矩对比

由图可知，F17～F21上部结构的延后施工大幅减小模板支撑体系计算荷载值，同时拱壳结构的轴力和弯矩也随之降低。在方案五～方案七下，模板支撑计算荷载值和拱壳结构内力明显减小，其中模板支撑计算荷载值每层减小幅度分别为20.12%、19.05%、18.17%；最大轴力减小幅度分别为4.68%、7.00%、5.78%；最大正负弯矩绝对值减小幅度分别为5.34%、7.18%、6.06%和5.50%、7.15%、6.05%，其原因为拱壳F19～F21的上部结构自重较大。在方案八～方案九下，模板支撑计算荷载值和拱壳结构内力减小速度变缓，其中模板支撑计算荷载值每层减小幅度分别为6.21%、2.23%；最大轴力减小幅度分别为3.28%、1.50%；最大正负弯矩绝对值减小幅度分别为3.63%、0.58%和3.73%、0.25%。主要是因为F17～F18拱壳上部结构自重相对较小。

进一步计算拱壳F17～F21上部结构施工顺序对成拱后结构最终内力的影响如表4所示。

表4 拱壳F17～F21上部结构施工对拱壳结构成形受力的影响

由表4可知，与优化前方案相比，5个方案中拱壳结构轴力最大偏差为6.95%，弯矩最大偏差为13.61%，表明拱壳F17～F21上部结构施工方案对拱壳结构成形内力计算结果有较小的影响。

根据B2拱壳模板支撑体系最大容许设计荷载值，方案六的模板支撑体系计算荷载值为30.36 kN/m2，满足设计要求，此时拱壳结构最大轴力为1 665.94 kN/m，降低幅值为11.68%，拱壳结构单位宽度最大正负弯矩绝对值分别为71.07 kN·m/m和91.25 kN·m/m，降低幅值分别为12.52%和12.65%，优化效果较明显。此时，若进一步延后施工，模板支撑计算荷载会继续减小，但同时会带来工期加长的不利影响，故选择方案六为最终优化方案。

进一步对优化后结构受力分析，最不利工况下，即结构施工F21时拱壳结构的轴力和弯矩云图如图16、图17所示。由内力云图可知，最大轴力为1 665.94 kN/m，出现在右侧拱壳底部F1层位置；单位宽度最大正负弯矩分别为71.07 kN·m/m和91.25 kN·m/m，出现在F2～F4位置，均满足结构承载力要求。

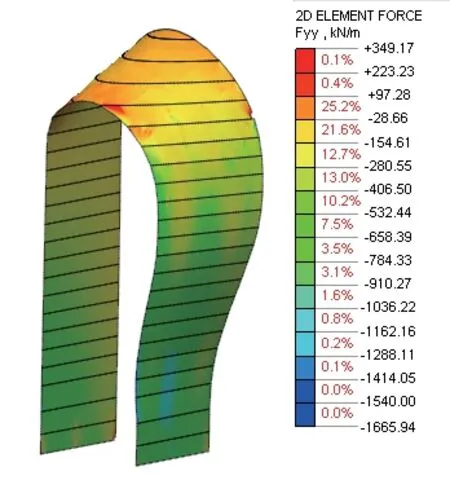
图16 施工F21时拱壳Y方向单位宽度轴力

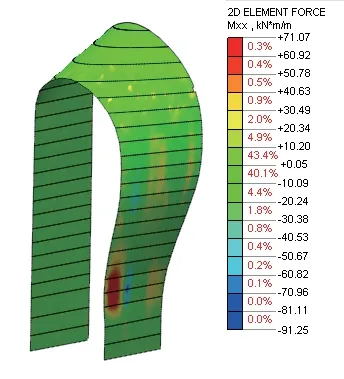
图17 施工F21时拱壳X方向单位宽度弯矩

4 结语

1）模板拆卸方案四通过对F12～F14模板进行延迟拆卸优化，与方案一相比，下层的模板可以得到及时有效的拆卸，但是并未对模板支撑计算荷载值和拱壳结构内力造成影响。

2）上部结构施工方案六对F20～F21上部结构延迟施工，能大幅减小模板支撑体系计算荷载值并有效改善拱壳结构的内力值，同时对工期影响较小。与原方案相比，方案六模板支撑计算荷载值减小39.17%，拱壳结构单位宽度最大轴力降低11.68%，拱壳结构单位宽度最大正负弯矩绝对值分别下降12.52%和12.65%。

3）按施工阶段分析和一次成拱分析对结构的最终内力状态存在一定影响，不考虑施工阶段分析会低估结构的内力水平。

4）采用方案六对大型复杂随形拱壳结构进行施工，不仅可以满足高空模板支撑体系的荷载设计要求和拱壳结构的安全性要求，同时可以有效控制工期。

经过方案比选，现场施工区段及工况按方案六采用钢平台转换支撑技术，用桥梁施工用的贝雷架与钢柱、附墙件形成钢平台，在其上部搭设扣件式钢管满堂架结构。方案实施成功，模架体系在随形拱壳结构逐层现浇合拢过程中无沉降变形，安全可靠。