Study of Degenerate Poly-Bernoulli Polynomials by λ-Umbral Calculus

Lee-Chae Jang,Dae San Kim,Hanyoung Kim,Taekyun Kim,⋆and Hyunseok Lee

1Graduate School of Education,Konkuk University,Seoul,143-701,Korea

2Department of Mathematics,Sogang University,Seoul,121-742,Korea

3Department of Mathematics,Kwangwoon University,Seoul,139-701,Korea

ABSTRACT Recently,degenerate poly-Bernoulli polynomials are defined in terms of degenerate polyexponential functions by Kim-Kim-Kwon-Lee.The aim of this paper is to further examine some properties of the degenerate poly-Bernoulli polynomials by using three formulas from the recently developed‘λ-umbral calculus.’In more detail,we represent the degenerate poly-Bernoulli polynomials by Carlitz Bernoulli polynomials and degenerate Stirling numbers of the first kind,by fully degenerate Bell polynomials and degenerate Stirling numbers of the first kind,and by higherorder degenerate Bernoulli polynomials and degenerate Stirling numbers of the second kind.

KEYWORDS Degenerate poly-Bernoulli polynomials;degenerate polyexponential functions; λ-umbral calculus

1 Introduction

Carlitz investigated the degenerate Bernoulli and Euler polynomials and numbers in[1,2],as degenerate versions of the ordinary Bernoulli and Euler polynomials and numbers.In recent years,studying degenerate versions of some special numbers and polynomials has received increased attention by mathematicians with their interests not only in combinatorial and arithmetic properties but also in applications to differential equations,identities of symmetry and probability theory(see[3–9]and references therein).Quite a few different methods have been employed in investigating degenerate versions of special numbers and polynomials,which include combinatorial methods,generating functions,umbral calculus techniques,p-adic analysis,differential equations,special functions,probability theory and analytic number theory.

Gian-Carlo Rota laid a completely rigorous foundation for umbral calculus in the 1970s,which had been in a state of manipulating sequences by a symbolic technique.The Rota’s theory is based on the modern concepts like linear functionals and differential operators.In addition,the central position in the theory is occupied by the Sheffer sequences whose generating functions are given in terms of the usual exponential function(see[10–12]).Thus one may say that umbral calculus is the study of Sheffer sequences.The impetus for[4]started from the simple question,what if the usual exponential function is replaced by the degenerate exponential functions in(1).This question arises very naturally in light of the regained recent interests in degenerate special numbers and polynomials.As it turns out,it amounts to replacing the linear functionals by the family ofλ-linear functionals in(11),and the differential operators by the family ofλ-differential operators in(12).Furthermore,these replacements led to defineλ-Sheffer sequences which are charactered by the desired generating functions in(18).Hence one may say thatλ-umbral calculus is the study ofλ-Sheffer sequences.

The motivation of the present research is to demonstrate its usefulness of the newly developedλ-umbral calculus in studying some degenerate special numbers and polynomials.Recently,degenerate polyexponential functions were introduced(see[13,14])and degenerate poly-Bernoulli polynomials were defined by means of the degenerate polyexponential functions(see(2),(10)),and some properties of the degenerate poly-Bernoulli polynomials were investigated(see[8]).The aim of this paper is to further examine the degenerate poly-Bernoulli polynomials using the abovementionedλ-linear functionals andλ-differential operators.In more detail,these polynomials are investigated by three different tools,namely a formula about representing aλ-Sheffer sequence by another(see(20)),a formula obtained from the generating functions ofλ-Sheffer sequences(see Theorem 1)and a formula arising from the definitions forλ-Sheffer sequences(see Theorems 6,8).Then,among other things,we represent the degenerate poly-Bernoulli polynomials by Carlitz Bernoulli polynomials and degenerate Stirling numbers of the first kind,by fully degenerate Bell polynomials and degenerate Stirling numbers of the first kind,and by higher-order degenerate Bernoulli polynomials and degenerate Stirling numbers of the second kind.

The rest of this section is devoted to recalling the necessary facts that are needed throughout the paper,which includes very brief review onλ-umbral calculus.

For anyλ∈R,the degenerate exponential functions are defined by

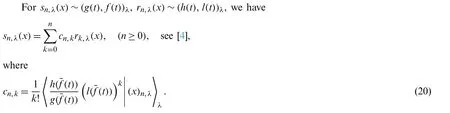
2 Degenerate Poly-Bernoulli Polynomials Arising from Degenerate Polyexponential Function

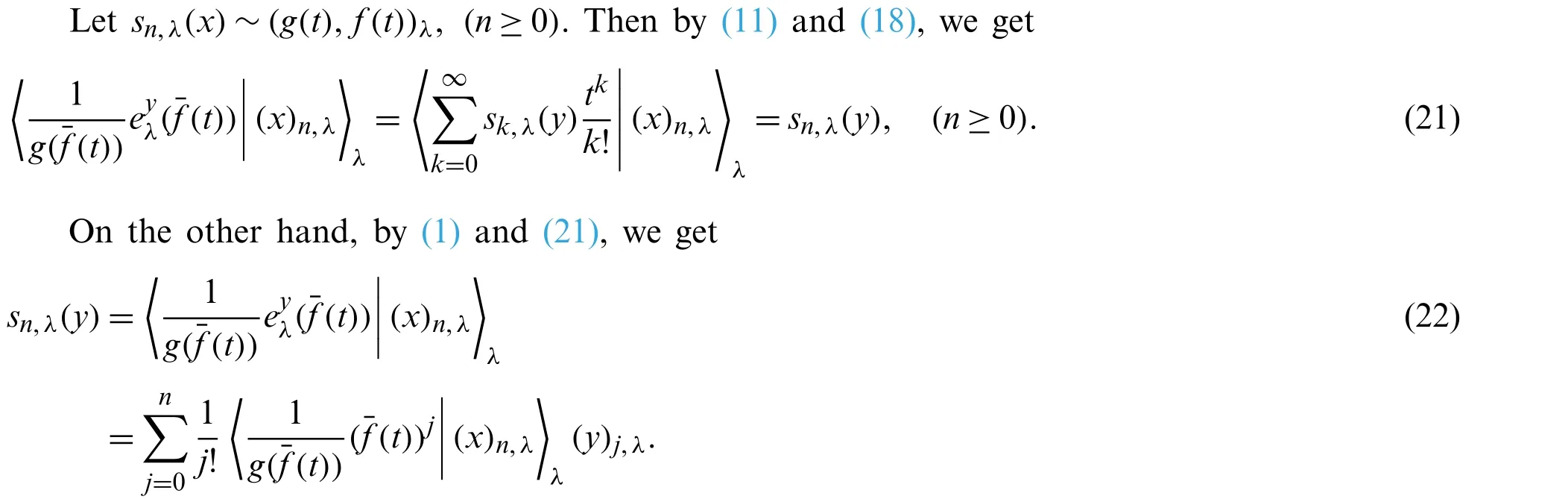
Figure 1:

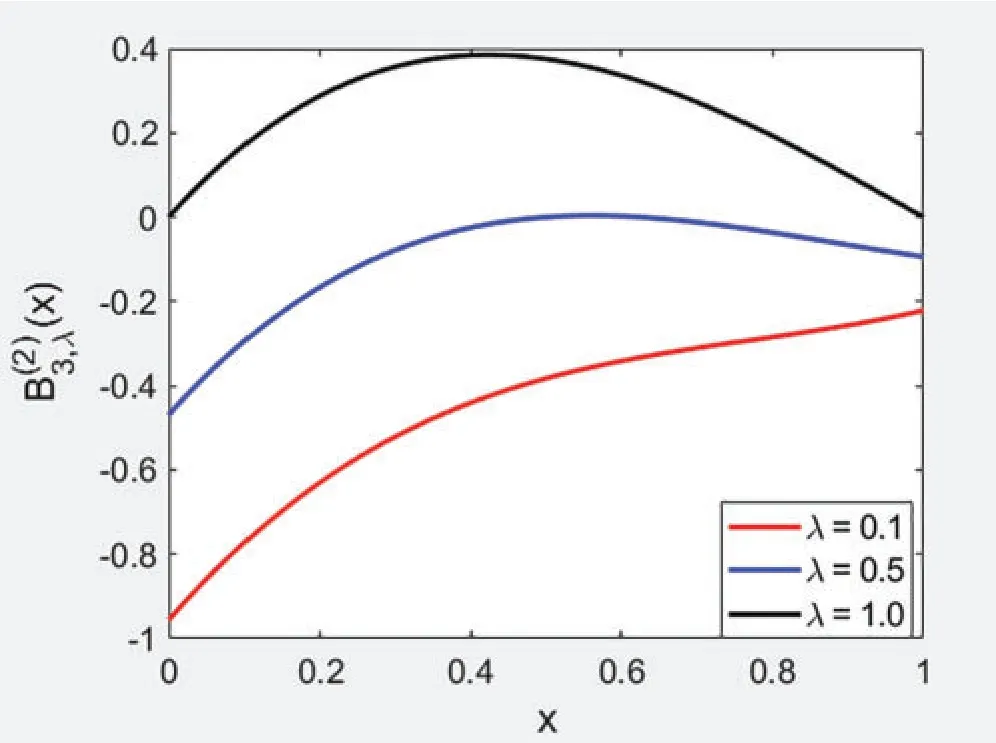
Figure 2:

Figure 3:

3 Conclusion

The study of degenerate versions of some special polynomials was initiated by Carlitz and has spurred increased interests by some mathematicians in recent times.This study unveiled many interesting results,not only from arithmetical and combinatorial perspectives but also in their applications to differential equations,identities of symmetry and probability theory.

Recently,theλ-umbral calculus was developed starting from the question,what if the usual exponential function is replaced by the degenerate exponential functions in the generating function of a Sheffer sequence.This question led us to the introduction of the concepts likeλ-linear functionals,λ-differential operators andλ-Sheffer sequences.

In this paper,the degenerate poly-Bernoulli polynomials were investigated using three different tools,namely a formula about representing aλ-Sheffer sequence by another,a formula coming from the generating functions ofλ-Sheffer sequences and a formula arising from the definitions forλ-Sheffer sequences.Then,among other things,we represented the degenerate poly-Bernoulli polynomials by Carlitz Bernoulli polynomials and degenerate Stirling numbers of the first kind,by fully degenerate Bell polynomials and degenerate Stirling numbers of the first kind,and by higherorder degenerate Bernoulli polynomials and degenerate Stirling numbers of the second kind.

As one of our future projects,we want to continue to investigate the degenerate special numbers and polynomials by using the recently developedλ-umbral calculus.

Acknowledgement:The authors thank to Jangjeon Institute for Mathematical Science for the support of this research.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.