Neutrosophic N-Structures Applied to Sheffer Stroke BL-Algebras

Tugce Katican,Tahsin Oner,Akbar Rezaeiand Florentin Smarandache

1Department of Mathematics,Ege University,Izmir,35100,Turkey

2Department of Mathematics,Payame Noor University,Tehran,19395-4697,Iran

3Department of Mathematics and Science,University of New Mexico,Gallup,87301,NM,USA

ABSTRACT In this paper,we introduce a neutrosophic N-subalgebra,a(ultra)neutrosophic N-filter,level sets of these neutrosophic N-structures and their properties on a Sheffer stroke BL-algebra.By defining a quasi-subalgebra of a Sheffer stroke BL-algebra,it is proved that the level set of neutrosophic N-subalgebras on the algebraic structure is its quasi-subalgebra and vice versa.Then we show that the family of all neutrosophic N-subalgebras of a Sheffer stroke BL-algebra forms a complete distributive lattice.After that a(ultra)neutrosophic N-filter of a Sheffer stroke BL-algebra is described,we demonstrate that every neutrosophic N-filter of a Sheffer stroke BL-algebra is its neutrosophic N-subalgebra but the inverse is generally not true.Finally,it is presented that a level set of a(ultra)neutrosophic N-filter of a Sheffer stroke BL-algebra is also its(ultra)filter and the inverse is always true.Moreover,some features of neutrosophic N-structures on a Sheffer stroke BL-algebra are investigated.

KEYWORDS Sheffer stroke BL-algebra;(ultra)filter;neutrosophic N-subalgebra;(ultra)neutrosophic N-filter

1 Introduction

Fuzzy set theory,which has the truth(t)(membership)function and state positive meaning of information,is introduced by Zadeh[1]as a generalization the classical set theory.This led scientists to find negative meaning of information.Hence,intuitionistic fuzzy sets[2]which are fuzzy sets with the falsehood(f)(nonmembership)function were introduced by Atanassov.However,there exist uncertainty and vagueness in the language,as well as positive ana negative meaning of information.Thus,Smarandache defined neutrosophic sets which are intuitionistic fuzzy sets with the indeterminacy/neutrality(i)function[3,4].Thereby,neutrosophic sets are determined on three components:(t,i,f):(truth,indeterminacy,falsehood)[5].Since neutrosophy enables that information in language can be comprehensively examined at all points,many researchers applied neutrosophy to different theoretical areas such as BCK/BCI-algebras,BE-algebras,semigroups,metric spaces,Sheffer stroke Hilbert algebras and strong Sheffer stroke non-associative MValgebras[6–15]so as to improve devices imitating human behaviours and thoughts,artificial intelligence and technological tools.

Sheffer stroke(or Sheffer operation)was originally introduced by Sheffer[16].Since Sheffer stroke can be used by itself without any other logical operators to build a logical system which is easy to control,Sheffer stroke can be applied to many logical algebras such as Boolean algebras[17],ortholattices[18],Sheffer stroke Hilbert algebras[19].On the other side,BL-algebras were introduced by Hájek as an axiom system of his Basic Logic(BL)for fuzzy propositional logic,and he widely studied many types of filters[20].Moreover,Oner et al.[21]introduced BL-algebras with Sheffer operation and investigated some types of(fuzzy)filters.

We give fundamental definitions and notions about Sheffer stroke BL-algebras,N-functions and neutrosophicN-structures defined by these functions on a crispy setX.Then a neutrosophicN-subalgebra and a(τ,γ,ρ)-level set of a neutrosophicN-structure are presented on Sheffer stroke BL-algebras.By defining a quasi-subalgebra of a Sheffer stroke BL-algebra,it is proved that every(τ,γ,ρ)-level set of a neutrosophicN-subalgebra of the algebra is the quasi-subalgebra and the inverse is true.Also,we show that the family of all neutrosophicN-subalgebras of this algebraic structure forms a complete distributive lattice.Some properties of neutrosophicNsubalgebras of Sheffer stroke BL-algebras are examined.Indeed,we investigate the case whichN-functions defining a neutrosophicN-subalgebra of a Sheffer stroke BL-algebra are constant.Moreover,we define a(ultra)neutrosophicN-filter of a Sheffer stroke BL-algebra byN-functions and analyze many features.It is demonstrated that(τ,γ,ρ)-level set of a neutrosophicN-filter of a Sheffer stroke BL-algebra is its filter but the inverse does not hold in general.In fact,we propound that(τ,γ,ρ)-level set of a(ultra)neutrosophicN-filter of a Sheffer stroke BL-algebra is its(ultra)filter and the inverse is true.Finally,new subsets of a Sheffer stroke BL-algebra are defined by theN-functions and special elements of the algebra.It is illustrated that these subsets are(ultra)filters of a Sheffer stroke BL-algebra for the(ultra)neutrosophicN-filter but the special conditions are necessary to prove the inverse.

2 Preliminaries

In this section,basic definitions and notions on Sheffer stroke BL-algebras and neutrosophicN-structures.

Definition 2.1.[18]LetH=〈H,|〉be a groupoid.The operation |is said to be aSheffer stroke(or Sheffer operation)if it satisfies the following conditions:

(S1)x|y=y|x,

(S2)(x|x)|(x|y)=x,

(S3)x|((y|z)|(y|z))=((x|y)|(x|y))|z,

(S4)(x|((x|x)|(y|y)))|(x|((x|x)|(y|y)))=x.

Definition 2.2.[21]A Sheffer stroke BL-algebra is an algebra(C,∨,∧,|,0,1)of type(2,2,2,0,0)satisfying the following conditions:

(sBL−1)(C,∨,∧,0,1)is a bounded lattice,

(sBL−2)(C,|)is a groupoid with the Sheffer stroke,

(sBL−3)c1∧c2=(c1|(c1|(c2|c2)))|(c1|(c1|(c2|c2))),

(sBL−4)(c1|(c2|c2))∨(c2|(c1|c1))=1,

for allc1,c2∈C.

1=0|0 is the greatest element and 0=1|1 is the least element ofC.

Proposition 2.1.[21]In any Sheffer stroke BL-algebraC,the following features hold,for allc1,c2,c3∈C:

(1)c1|((c2|(c3|c3))|(c2|(c3|c3)))=c2|((c1|(c3|c3))|(c1|(c3|c3))),

(2)c1|(c1|c1)=1,

(3)1|(c1|c1)=c1,

(4)c1|(1|1)=1,

(5)(c1|1)|(c1|1)=c1,

(6)(c1|c2)|(c1|c2)≤c3⇔c1≤c2|(c3|c3)

(7)c1≤c2iffc1|(c2|c2)=1,

(8)c1≤c2|(c1|c1),

(9)c1≤(c1|c2)|c2,

(10)(a)(c1|(c1|(c2|c2)))|(c1|(c1|(c2|c2)))≤c1,

(b)(c1|(c1|(c2|c2)))|(c1|(c1|(c2|c2)))≤c2.

(11)Ifc1≤c2,then

(i)c3|(c1|c1)≤c3|(c2|c2),

(ii)(c1|c3)|(c1|c3)≤(c2|c3)|(c2|c3),

(iii)c2|(c3|c3)≤c1|(c3|c3).

(12)c1|(c2|c2)≤(c3|(c1|c1))|((c3|(c2|c2))|(c3|(c2|c2))),

(13)c1|(c2|c2)≤(c2|(c3|c3))|((c1|(c3|c3))|(c1|(c3|c3))),

(14)((c1∨c2)|c3)|((c1∨c2)|c3)=((c1|c3)|(c1|c3))∨((c2|c3)|(c2|c3)),

(15)c1∨c2=((c1|(c2|c2))|(c2|c2))∧((c2|(c1|c1))|(c1|c1)).

Lemma 2.1.[21]LetCbe a Sheffer stroke BL-algebra.Then

(c1|(c2|c2))|(c2|c2)=(c2|(c1|c1))|(c1|c1),

for allc1,c2∈C.

Corollary 2.1.[21]LetCbe a Sheffer stroke BL-algebra.Then

c1∨c2=(c1|(c2|c2))|(c2|c2),

for allc1,c2∈C.

Lemma 2.2.[21]LetCbe a Sheffer stroke BL-algebra.Then

c1|((c2|(c3|c3))|(c2|(c3|c3)))=(c1|(c2|c2))|((c1|(c3|c3))|(c1|(c3|c3))),

for allc1,c2,c3∈C.

Definition 2.3.[21]A filter ofCis a nonempty subsetP⊆Csatisfying

(SF−1)ifc1,c2∈P,then(c1|c2)|(c1|c2)∈P,

(SF−2)ifc1∈Pandc1≤c2,thenc2∈P.

Proposition 2.2.[21]LetPbe a nonempty subset ofC.ThenPis a filter ofCif and only if the following hold:

(SF−3)1 ∈P,

(SF−4)c1∈Pandc1|(c2|c2)∈Pimplyc2∈P.

Definition 2.4.[21]LetPbe a filter ofC.ThenPis called an ultra filter ofCif it satisfiesc∈Porc|c∈P,for allc∈C.

Lemma 2.3.[21]A filterPofCis an ultra filter ofCif and only ifc1∨c2∈Pimpliesc1∈Porc2∈P,for allc1,c2∈C.

Definition 2.5.[8]F(X,[−1,0])denotes the collection of functions from a setXto[−1,0]and an element ofF(X,[−1,0])is called a negative-valued function fromXto[−1,0](briefly,N-function onX).AnN-structure refers to an ordered pair(X,f)ofXandN-functionfonX.

Definition 2.6.[12]A neutrosophicN-structure over a nonempty universeXis defined by

whereTN,INandFNareN-functions onX,called the negative truth membership function,the negative indeterminacy membership function and the negative falsity membership function,respectively.

Every neutrosophicN-structureXNoverXsatisfies the condition(∀x∈X)(−3 ≤TN(x)+IN(x)+FN(x)≤0).

Definition 2.7.[13]LetXNbe a neutrosophicN-structure on a setXandτ,γ,ρbe any elements of[−1,0]such that −3 ≤τ+γ+ρ≤0.Consider the following sets:

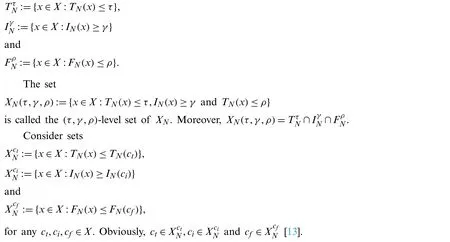
3 Neutrosophic N-Structures

In this section,neutrosophicN-subalgebras and neutrosophicN-filters on Sheffer stroke BLalgebras.Unless otherwise specified,Cdenotes a Sheffer stroke BL-algebra.

Definition 3.1.A neutrosophicN-structureCNon a Sheffer stroke BL-algebraCis called a neutrosophicN-subalgebra ofCif the following condition is valid:

for allc1,c2∈C.

Example 3.1.Consider a Sheffer stroke BL-algebraCwhere the setC={0,a,b,c,d,e,f,1}and the Sheffer operation |,the join operation ∨and the meet operation ∧onChas the Cayley tables in Tab.1[21].Then a neutrosophicN-structure

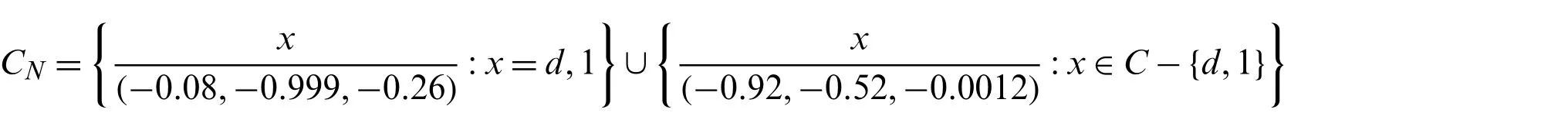
onCis a neutrosophicN-subalgebra ofC.

Table 1:Tables of the Sheffer operation |,the join operation ∨and the meet operation ∧on C

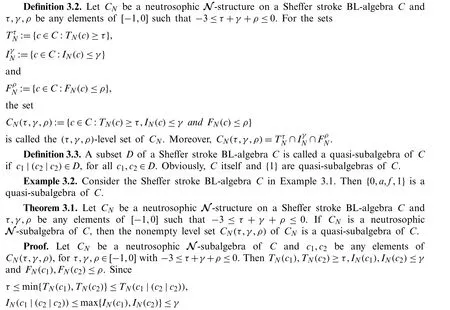
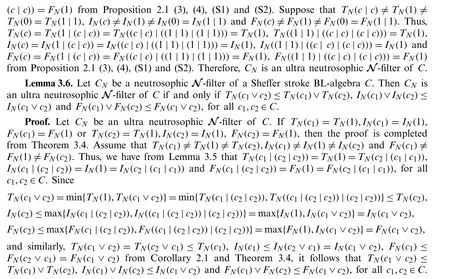
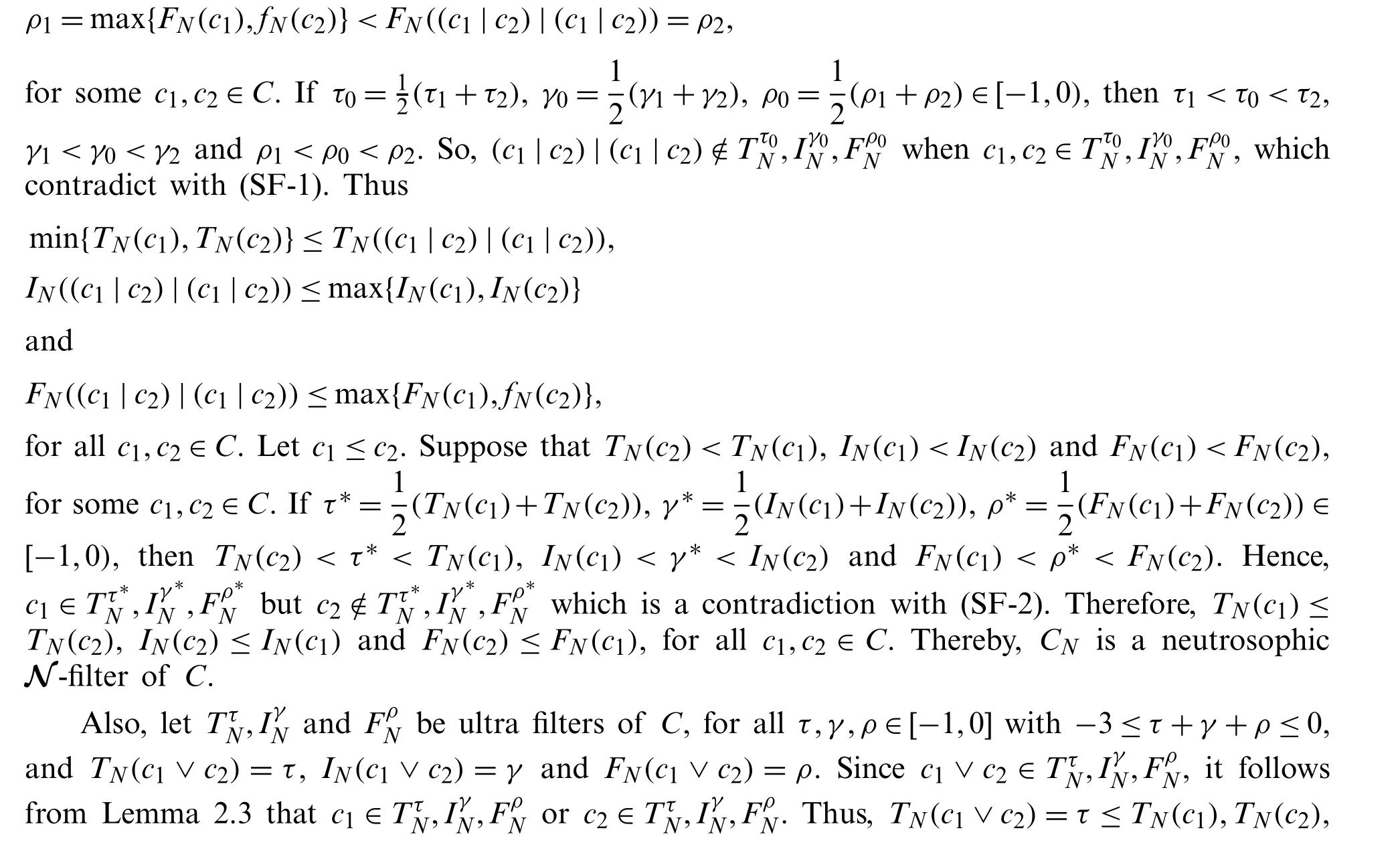
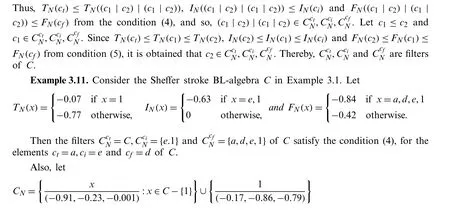
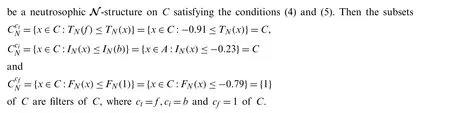
4 Conclusion

Acknowledgement:The authors are thankful to the referees for a careful reading of the paper and for valuable comments and suggestions.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.