Subdivision Surface-Based Isogeometric Boundary Element Method for Steady Heat Conduction Problems with Variable Coefficient

Xiuyun Chen,Xiaomeng Yin,Kunpeng Li,Ruhui Cheng,Yanming Xu,4,⋆and Wei Zhang

1School of Architectural Engineering,Huanghuai University,Zhumadian,463003,China

2College of Intelligent Construction,Wuchang University of Technology,Wuhan,430223,China

3College of Civil Engineering and Architecture,China Three Gorges University,Yichang,443000,China

4CAS Key Laboratory of Mechanical Behavior and Design of Materials,Department of Modern Mechanics,University of Science and Technology of China,Hefei,230026,China

ABSTRACT The present work couples isogeometric analysis(IGA)and boundary element methods(BEM)for three dimensional steady heat conduction problems with variable coefficients.The Computer-Aided Design(CAD)geometries are built by subdivision surfaces,and meantime the basis functions of subdivision surfaces are employed to discretize the boundary integral equations for heat conduction analysis.Moreover,the radial integration method is adopted to transform the additional domain integrals caused by variable coefficients to the boundary integrals.Several numerical examples are provided to demonstrate the correctness and advantages of the proposed algorithm in the integration of CAD and numerical analysis.

KEYWORDS Subdivision surface;isogeometric boundary element method;heat conduction;radial integration

1 Introduction

Since the pioneering work of Hughes et al.[1],isogeometric analysis(IGA)has attracted extensive attention from academia and industry.Different from the traditional numerical methods based on Lagrange polynomials,IGA employs the same basis functions used for geometric modeling in Computer-Aided Design(CAD),such as Non-Uniform Rational B-splines(NURBS)to discretize the unknown physical fields in Partial Differential Equations.Due to the capability of integrating CAD and numerical analysis,IGA is able to eliminate cumbersome meshing procedures,guaranteeing geometric exactness,and offering high-order continuous approximation and flexible refinement schemes[2–6].In order to ease the implementation of IGA,Bézier extraction operation[7]is introduced,which also accelerates the evaluation of basis functions significantly.

The concept of IGA was first proposed in the context of finite element methods(FEM).Its application in engineering practice for complex geometries is limited due to the volume parameterization of FEM conflicts with the boundary representation of CAD.On the contrary,the boundary element method(BEM)only needs boundary parameterization and thus is naturally compatible with CAD model[8–12].The isogeometric boundary element method(IGABEM)has been successfully applied to many fields,including linear elasticity[13–16],potential problems[17–20],fracture mechanics[21–25],electromagnetics[26],acoustics[27–32],structural optimization[33–37].

Heat conduction is of paramount importance in engineering.IGABEM based on NURBS was applied to 3D steady thermal conduction problems for a medium with non-homogenous inclusions[38,39]and transient heat conduction problems with heat sources[40–46].In the present paper,we adopts IGABEM based on subdivision surfaces for simulating steady heat conduction problems with variable coefficients.The subdivision surface method is a CAD technology which was first proposed by Catmull et al.[47].Compared to NURBS or other CAD modeling techniques,a salient feature of the subdivision surface method is that it is capable of constructing water-tight geometries and address extraordinary(or irregular)points[48].Cirak et al.[49]combined the subdivision surface method with the FEM to simulate the deformation of thin shell structures.Green et al.[50]put forward a multi-level method based on subdivision surfaces for accelerating the analysis of large-scale thin shell problems.The multi-resolution subdivision surfaces were also used for structural shape optimization in electromagnetic fields[51].For heat conduction problems with variable thermal conductivity coefficients,an addition domain integral term appears in the boundary integral equations.To solve this problem,the radial basis function method(RBF)was proposed to transform the domain integral to the boundary integral in conventional BEM[52,53].Such RBF method is also incorporated to the present work with IGABEM.

The remainder of the paper is organized as follows.The Catmull–Clark subdivision surface method is introduced in Section 2.The IGABEM with subdivision surfaces is used for solution of heat conduction with variable coefficient in Section 3.Then,several numerical examples are discussed in Section 4,followed by the conclusion in Section 5.

2 Subdivision Surface Method Based on Catmull–Clark

Subdivision surface is defined as the limit of an infinite refinement or subdivision process.Each new subdivision step produces a new mesh with more polygonal elements and smoother geometries.By repeatedly refining the initial polygon mesh,a series of meshes that approach the final subdivision surface is generated.The subdivision surface inherits the reconfigurability of spline curve,so that all control meshes generated in subdivision process can accurately represent the same spline surface.An important technical advance in subdivision surfaces is to generate limiting surfaces by constructing an elementwise mapping from the subdivided meshes.In this way,the subdivided meshes play the same role as control grids of NURBS in geometry modeling,and the limiting surface resembles the physical surface in NURBS.

In this work we consider the quadrilateral subdivision surfaces proposed by Catmull–Clark.The Catmull–Clark subdivision scheme is an extension of bicubic uniform B-splines.Catmull–Clark subdivision algorithm subdivides each quadrilateral element into four sub-quadrilateral elements(1–4 splitting)as shown in Fig.1.After continuous subdivision operation,the ultimate surface is obtained.

Figure 1:Catmull–Clark subdivision process

Let us set the original mesh subdivision level ask,and then subdivide it intok+ 1 level.The vertices on theklevel mesh are weighted on their patches to obtain new vertices on thek+ 1 level mesh,which are represented by the symbol “V”.Four new vertices are inserted at the midpoints of four edges at every element for theklevel mesh,which are represented by the symbol “E”.In addition,a new vertex is inserted at the center of every element for theklevel mesh,which is represented by the symbol “F”.An edge passing through a “V” vertex on theklevel mesh is called this vertex’s adjacent edge.The number of adjacent edges to a vertex is called a valencenvof this vertex.Ifnv= 4,the vertex is called a regular vertex as shown in Fig.2(blue point),otherwise it is called an irregular vertex as shown in Fig.2(red point),and the symbol “u” denotes the valencenvof Point 1.

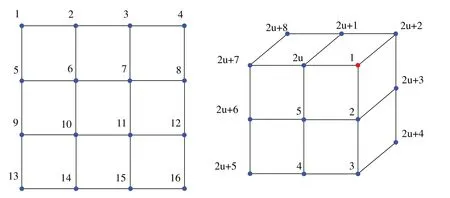
Figure 2:The regular and irregular points of Catmull–Clark subdivision surface

A quadrilateral mesh can be divided into four sub-elements by inserting a new point in the middle of each edge and inside the element,which are called “E” and “F”,respectively.In addition,the position of original points called “V” is moved to construct smooth surface flexibly.

The coordinates of these vertices “V”,“E” and “F” on thek+ 1 level mesh generated after one subdivision are obtained from that on theklevel mesh by interpolation operation,as follows:

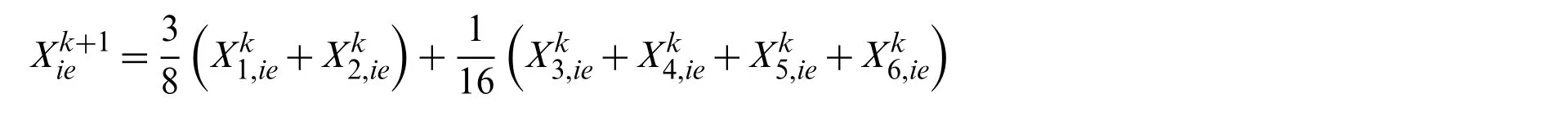
whereandγ= 1 −α−β.Similar to h-refinement characteristic of NURBS,the same surface model can be obtained by fitting any level of subdivision mesh,which is consistent with the limit subdivision model.Thus,it eliminates the need of a limit mesh for numerical analysis.The characteristics of geometric control points(regular points attached to four quadrilateral elements or irregular points)determine the characteristics of the mesh,which determines the selection of fitting technology.A cell containing only regular points is called a regular cell,otherwise it is called an irregular cell.For regular elements,there are direct explicit basis functions for surface fitting and physical field interpolation.However,for irregular element,there is no explicit basis function,thereby requiring special construction.

The idea of limit subdivision is used to subdivide the irregular elements locally and repeatedly through the following steps:(1)introducing subdivision matrices to establish the relationship between the hierarchical sub units and the parent units,(2)obtaining the eigenvector and eigenvalue of the matrix by Fourier transformation of the subdivision matrix,(3)storing the information of the hierarchical regular sub units by using the subdivision matrix,the picking matrix and the regular unit,and(4)building the base function of the original irregular parent unit 3.After constructing the basis function of the irregular element,the surface model corresponding to the whole mesh can be constructed by the fitting operation,and the model hasC2continuity at the regular point andC1continuity at the irregular point.

In each regular quadrilateral there are sixteen quartic non-zero basis functions associated with its and neighbouring quadrilateral vertices,as shown in Fig.3.Hence,the surface coordinatesXewithin the quadrilateralecan be determined through

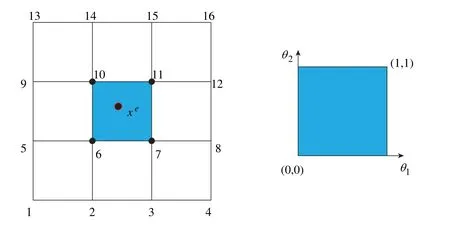
Figure 3:The Cartesian coordinates of the fitting element and the parameter field

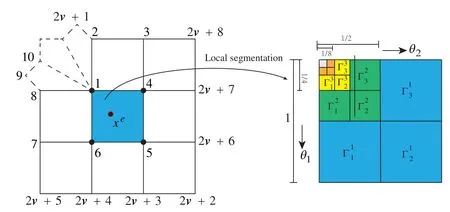
Figure 4:Local segmentation

3 IGABEM for Heat Conduction with Subdivision Surface

3.1 Governing Equation of Heat Conduction

By observing Eq.(11),we notice that the second and third terms are boundary integrals,but the last two terms are domain integrals.Although direct domain discretization methods can be used,the advantage of dimensionality reduction of BEM cannot be retained.Hence,in this work,the source term is not considered,and the RBF method is used to transform the domain integral caused by thermal conductivity into the boundary integral.

3.2 Transformation of Domain Integral Caused by Thermal Conductivity

The second domain integral in Eq.(11)contains the unknown variable ˆT(~y).The radial basis function is used to approximate the variable,as follows:

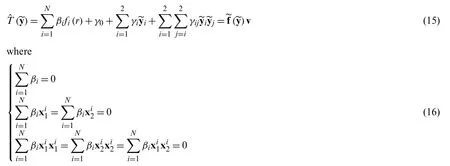
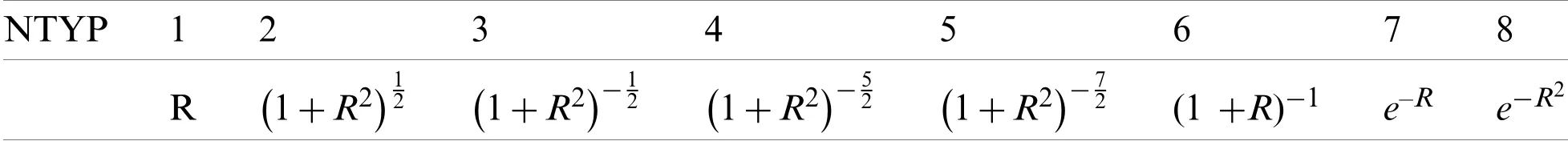
Table 1:Types of radial basis functions

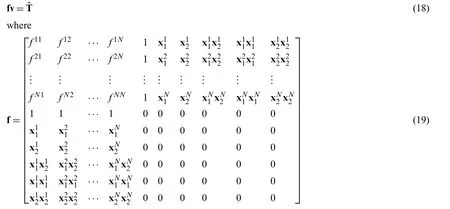
How to determine the coefficientsβandγis particularly important.It is difficult to obtain these coefficients directly.However,through a series of transformation operations,we can get the implicit expression of these coefficients.When the pointis set as collocation points in Eq.(15),by assembling them into matrix vector formulation,the following formula is obtained:

4 Numerical Examples

4.1 A Cube with Cylindrical Hole

In this section,we consider a cube with cylindrical hole.Catmull–Clark subdivision surface scheme is used to construct a smooth model.The initial model is shown in Fig.5a.The size of the cube is 0.5 m × 0.5 m × 0.5 m,and the radius of the cylinder in the middle of the cube is r = 0.125 m.Fig.5b shows the model after subdivision once and Fig.5c shows the model after subdivision twice.It is worth noting that although the control meshes at different subdivision levels are different,the surfaces obtained by fitting are the same and consistent with the limit subdivision mesh model.The temperature of the fluid in the cylinder is Tf= 293 K,and the convective heat transfer coefficient h = 1000 W/(m2· K)between the fluid and structure.The right surface of the structure with the maximum coordinate value in positive y-axis is subjected to constant heat flux q = 50000 W/m2.The other five surfaces are adiabatic.Material densityρ= 7800 kg/m3,specific heat capacity cp= 460 J/(kg · K),and thermal conductivity k = 500 W/(m · K).

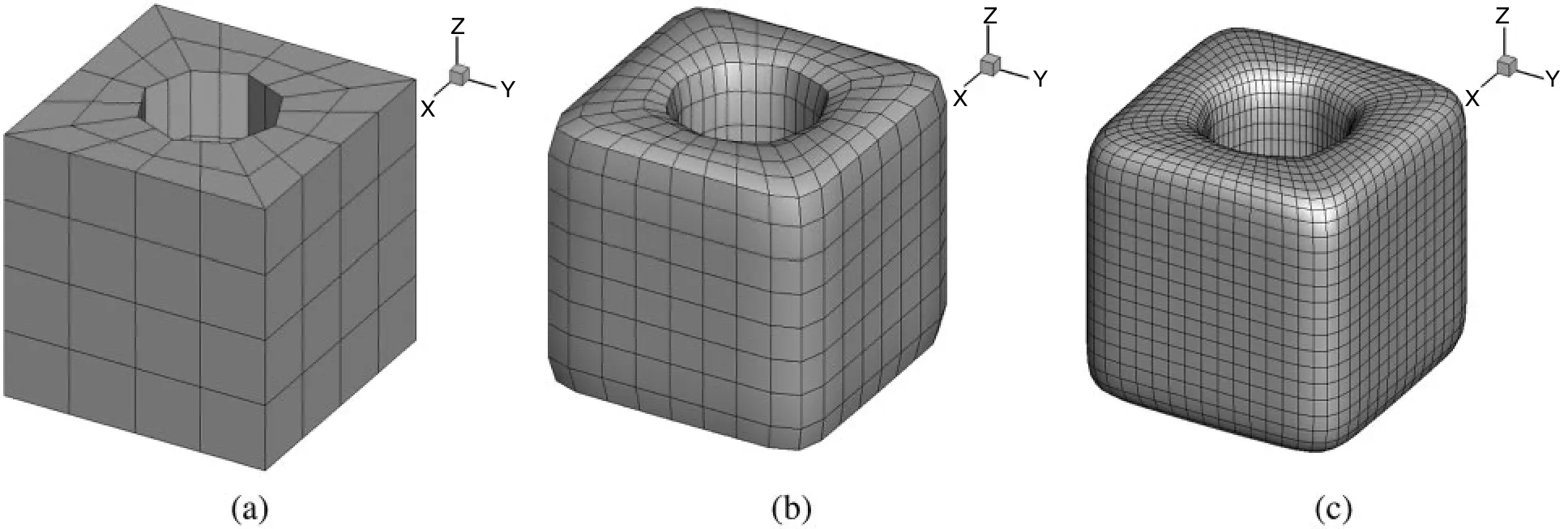
Figure 5:The cube model constructed by Catmull–Clark subdivision surface method.(a)Initial mesh(b)subdivision once(c)subdivision twice

Since there is no analytical solution to the problem,we compare the results of this algorithm proposed in this work with that of Fluent.In Fig.6a,the coordinates of the computing points is(0.25,y,0),andy∈[−0.25,0.25].The symbol “CC-IGABEM” denotes the numerical solution obtained from IGABEM with Catmull–Clark subdivision surfaces.In Fig.6b,the computing points withz= 0.25 are located on the circumference of the circular hole,whereθdenotes the angle between the vertical line from the computing point to the axis of the cylinder inside the structure and the x-axis.It can be seen that the results of the developed algorithm are consistent with those of fluent,which verifies the correctness of the algorithm.

We consider a problem with variable heat conduction coefficients.The thermal conductivity of the material is not a constant value,but satisfiesk=(400 + 200r)W/(m · K).The distribution of temperature on structural surface for constant coefficient and variable coefficient is shown in Figs.7a and 7b,respectively.It can be seen that the temperature field is symmetric alongxoyandzoyplanes,respectively.The right surface in contact with the constant heat flux has a higher temperature value than the left surface.

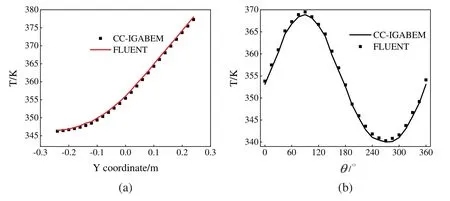
Figure 6:The temperature at several computing points obtained by using fluent and IGABEM with subdivision surface.(a)results at the points(0.25,y,0)(b)results at the points z= 0.25

Figure 7:Distribution of temperature on structural surface.(a)Temperature distribution for constant thermal conductivity(b)temperature distribution for variable thermal conductivity

The value of the temperature at the computing points in Fig.6a for homogeneous and heterogeneous materials are plotted in Fig.8.For these two different conditions,there is a small difference between the calculation results,which shows that the variable heat conductivity has an impact on the calculation results,and also demonstrates the ability of the algorithm in this paper for variable coefficient problems.

4.2 Example of Dumbbell Model

Consider a dumbbell model shown in Fig.9a.The top and bottom of the dumbbell is a hexahedron with a side length 0.08 m and height 0.08 m.The middle part of the dumbbell structure is a cylinder with a radius 0.04 m and height 0.16 m.

The top surface is subjected to constant heat fluxq= 50000 W/m2.The bottom of the structure contacts a heat source withTf= 293 K,and the convective heat transfer coefficienth= 1000 W/(m2· K).The other surfaces are adiabatic.Herein,material density isρ= 7800 kg/m3,heat capacity ratio iscp= 460 J/(kg · K),the thermal conductivity isk= 500 W/(m · K).

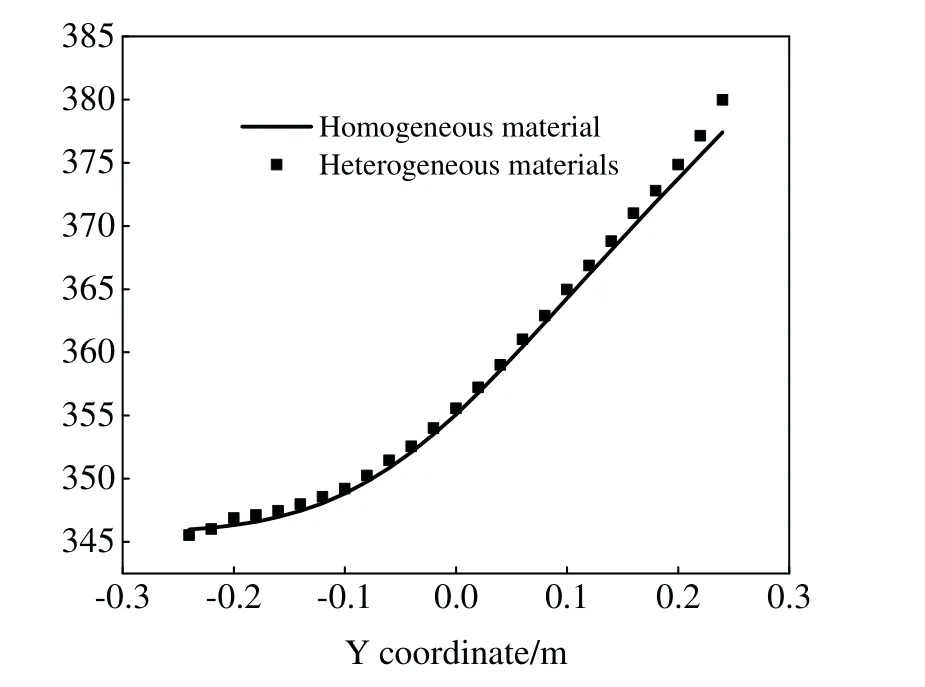
Figure 8:Distribution of temperature on structural surface

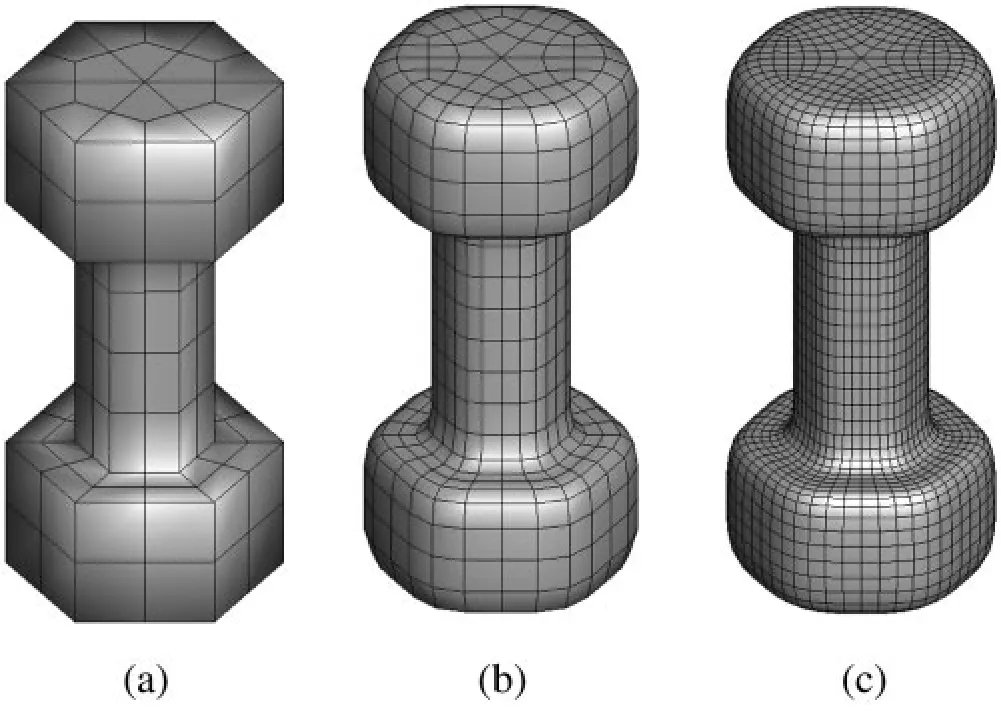
Figure 9:Initial cube and subdivision model of columnar body.(a)Initial mesh(b)subdivision once(c)subdivision twice

As shown in Fig.9,the initial mesh in Fig.9a is subdivided into denser grids,such as primary subdivision mesh in Fig.9b and secondary subdivision mesh in Fig.9c.Fig.10 shows the distribution of temperature on the structural surface with constant thermal conductivity and variable thermal conductivity,respectively.The thermal conductivity of the material in Fig.10b satisfiesk=(400 + 200r)W/(m · K).The variablerdenotes the distance from the point to the z-axis,which is the axis of symmetry in vertical direction.The temperature distribution decreases gradually along the z-axis.Although the temperature profiles corresponding to different thermal conductivities are very similar,the temperature values represented by the profiles show differences,as listed in Tab.2.

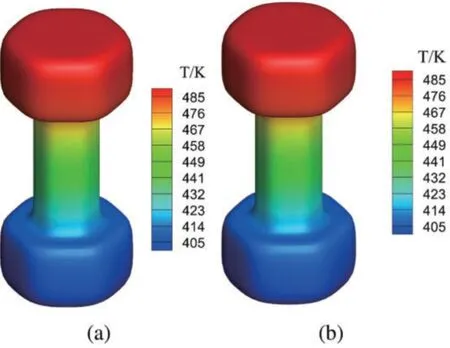
Figure 10:Temperature field with the change of thermal conductivity of columnar body.(a)Temperature distribution for constant thermal conductivity(b)temperature distribution for variable thermal conductivity

Table 2:The surface temperature changes along the z direction

5 Conclusions

In this work,we present a novel framework for solving three-dimensional steady-state heat conduction problems with IGABEM.The Catmull–Clark subdivision surface method is used to construct a smooth geometric model and discretizing boundary integral equations.The radial integration method is incorporated to transform the domain integral caused by variable coefficient into the boundary integral.The numerical simulation can be conducted directly from CAD model without needing a meshing procedure.The numerical results validate the accuracy of the method and demonstrate its ability of integrating CAD and numerical analysis.In the future,we will extend the algorithm to transient heat conduction problems.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.