节段预制混凝土斜拉桥索导管角度定位方法

林李龙

（中国铁路广州局集团有限公司 广州广东 511470）

1 引言

节段预制桥梁具有施工速度快、质量易控制、环境干扰小等优点，在桥梁工程建设中得到越来越多的推广应用［1］。在预制时将箱梁分成若干节段，依次在预制平台上浇筑。已预制好的梁段前移，作为下一梁段的匹配梁，待浇梁段预制完成后，匹配梁移至存梁区存放。待存放一定时间后将梁段运至桥梁现场进行节段拼装，直至全桥合龙。

节段预制施工方法在早期主要应用于混凝土梁式桥，逐步推广到混凝土斜拉桥上。与梁式桥相比，斜拉桥上斜拉索成为了重要受力构件，在梁段预制时需将斜拉索索导管预埋到梁段内。索导管安装角度准确定位，成为斜拉桥施工控制中的重要问题［2－4］。现有索导管安装定位方法主要是针对悬臂浇筑的混凝土斜拉桥［5－7］，不能将其直接应用于节段预制斜拉桥上。这是由于节段预制斜拉桥一般需建立预制场地的局部坐标系，在该局部坐标系下进行梁段定位和预制。由于局部坐标系与桥梁现场整体坐标系不同，如何准确计算索导管在预制局部坐标系下的角度，是需要解决的重点问题。

本文首先分析节段预制时影响索导管角度的因素，再推导各因素对应的角度修正公式，提出索导管安装角度的计算方法，并结合工程实例，对索导管安装角度修正结果进行探讨。

2 斜拉索导管角度修正分析

施工过程中，随着混凝土浇筑，斜拉索张拉及临时荷载变化，主梁位置会发生变化，索导管的位置和角度也会发生变化。因此，在索导管安装时，不能直接使用成桥状态下索导管的倾角来定位，需根据预拱度及施工产生的角度变化，对索导管角度进行修正，才能确保达到设计成桥目标。影响索导管角度的因素主要有主梁施工预拱度、索塔偏位、斜拉索垂度效应和梁轴向角度。

为了实现成桥线形，在梁段预制过程中需设置施工预拱度，这会要求索导管角度也相应改变。施工预拱度主要考虑结构自重、桥面铺装、预应力荷载、吊机荷载、拉索张拉和徐变等引起的变形。预拱度的设置会引起梁段转角变化，如图1所示。由于索导管与梁段固结成整体，主梁转角变化量可认为与梁段转角变化量相同，从而确定预拱度引起的索导管角度变化αpr：

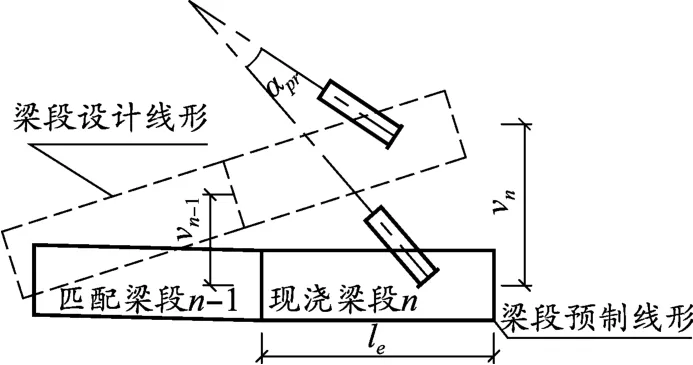
图1 索导管立面

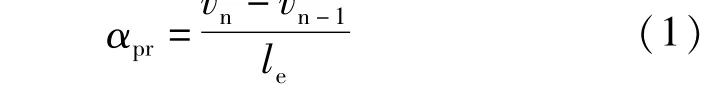
式中：le为梁段的长度；vn和vn－1分别为根据切线位移法得到的第n点和第n－1点竖向预拱度值。在计算预拱度时需考虑结构自重、桥面铺装重量、预应力张拉、斜拉索张拉、桥面吊机重量及收缩徐变等引起的变形和车辆活载引起的变形。为了准确计算这些变形，建立桥梁有限元模型，对每个施工阶段进行准确模拟。根据模拟分析结果，提取结构变形值。

在索力作用下，索塔发生变形，塔上拉索锚固点将发生竖向和纵向位移。为此梁上索导管角度也应进行相应调整，才能保证索塔和主梁的锚固点对中。由于索塔竖向位移值远小于索长lc，当塔上拉索锚固点发生竖向位移vt时，梁上索导管角度近似修正量αtv为：

当塔上锚固点发生纵向位移ut时，梁上索导管角度近似修正量αtu为：

式中：位移vt和ut均为按照桥梁有限元计算分析结果提取出的拉索锚固点位移值。

斜拉索由于自身重力作用，会产生一定下垂，其垂度大小也与索力有关。在索导管安装时，需考虑垂度效应引起的导管倾角变化αs，如图2所示。当索长小于300 m时，可假定拉索形状为抛物线形状［8－9］，计算倾角变化 αs：

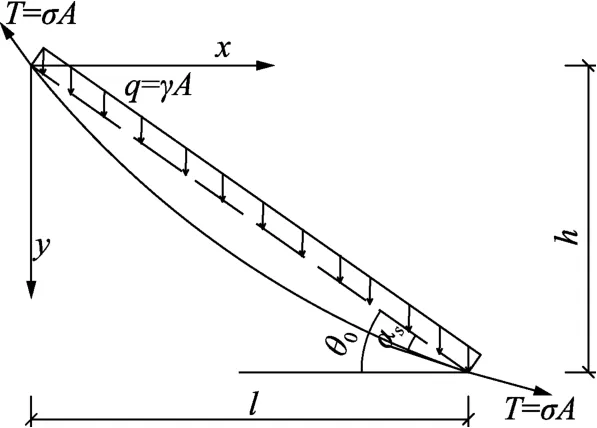
图2 斜拉索受力

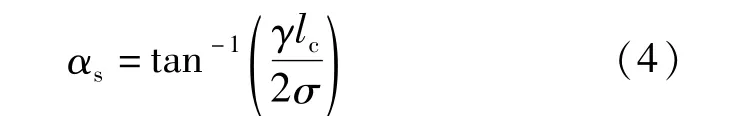
式中：γ为拉索容重；σ为拉索张拉应力。

当拉索长度较长时，在自重和张拉力作用下，拉索形状更接近于悬链线，应采用更为精确的悬链线理论求解 αs。其悬链线方程可表示为［10－12］：

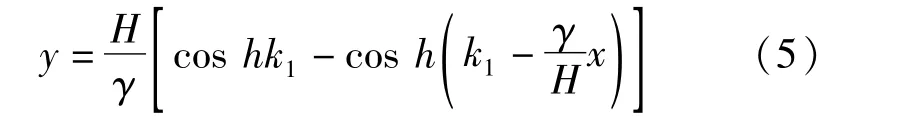
式中：H为拉索拉力的水平分力；k1为参数，其表达式为：

Tennant河地区主要为管状(筒状)。矿床总体在深部的蚀变作用为钠质蚀变组合，在中浅部为钾质蚀变组合，而在浅部则为绢云母化和硅化；以磁铁矿为主的矿化以钠质蚀变为主，以赤铁矿为主的矿化以钾质蚀变为主。该区有经济价值的金-铜-铋矿化大多数与单个富磁铁矿或其相当的氧化矿相伴，呈现高的航磁异常，矿体地表露头以褐铁矿为主，深部以磁铁矿为主，高品位的金通常位于铁矿体底部，呈细脉-浸染状产出。铁矿的形状从近于圆形到筒状，长轴通常沿着EW向的裂隙，产出于元古代变质细粒沉积层系中，部分含有浸染磁铁矿。

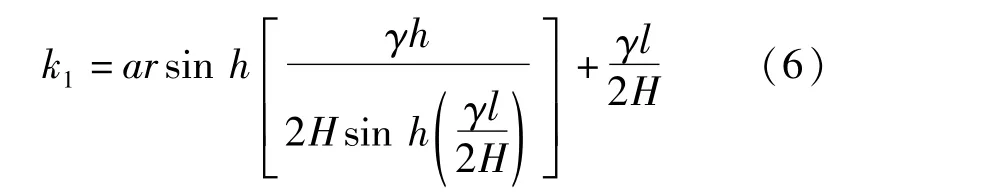
式中：h为拉索高度；l为拉索水平长度。

由式（5）可知：在拉索张拉力T确定的情况下，拉索悬链线索形和水平分力相互耦合；悬链线上每个点的斜率由水平分力所决定，而水平分力与张拉力又存在 H ＝Tcos（θ0－ αs）的关系，其中 θ0为索导管在成桥状态下的理论初始倾角。因此可利用水平分力与拉索斜率之间的关系建立迭代关系式，对水平分力H和拉索倾角修正值αs进行迭代求解。具体求解过程可参考文献［12］。

综合上述角度修正结果，可得索导管安装角度θd计算公式：

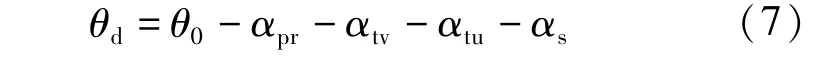
在梁段节段预制过程中，预制场地的坐标系往往是局部坐标系，其水平轴为沿梁段的轴线方向。所以在索导管埋设时安装角度以局部坐标系的角度给出，在局部坐标系下安装角度即为拉索切线与梁轴线的夹角θl：

式中：β为预制线形中梁段轴线与整体坐标系水平轴的夹角。

3 实例分析

广汕客专增江特大桥于DK65＋150～DK65＋450在增城市石滩镇跨越增江，主桥采用双塔双索面混凝土斜拉桥，孔跨布置为（48＋84＋260＋84＋48）m，含梁缝主桥全长526.3 m，如图3所示。主桥位于双向6‰的纵坡上，变坡点位于主跨跨中处，竖曲线半径为25 000 m，平面位于直线上。主梁采用节段预制胶拼法施工，混凝土梁预制节段标准长4 m，全桥共132个预制节段和1个合龙现浇梁段。

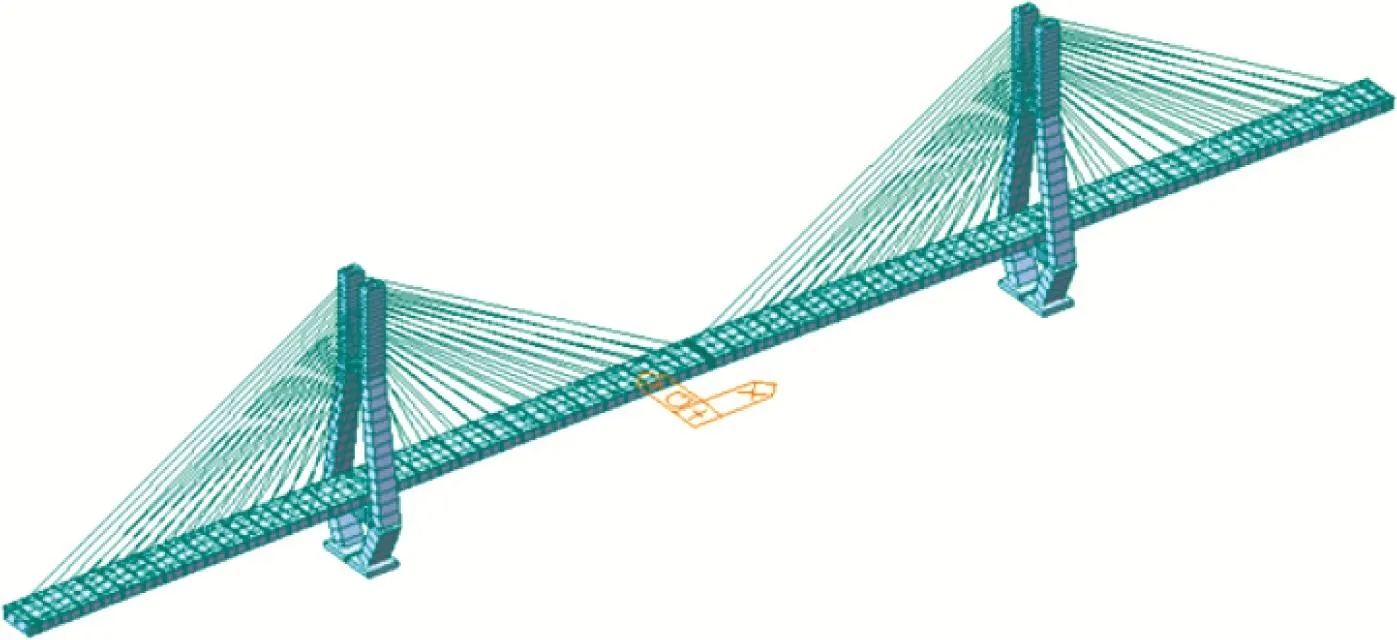
图3 增江特大桥模型

混凝土主梁采用单箱三室等高混凝土箱梁，受力形式为双边箱主梁，箱梁全宽14.4 m，中心处梁高4.0 m，斜拉索横向间距10.9 m，梁上锚固于双边箱内。主梁预应力布置采用节段拼装施工临时张拉纵向预应力、节段拼装施工过程用纵向预应力、体内纵横向局部预应力的混合布索体系。梁段预制后，主梁边跨采用支架拼装，边跨拼装完成后，中跨安装桥面吊机，进行梁段的悬臂拼装，同时安装并张拉斜拉索，逐段施工直至合龙。

根据设计提供的图纸，建立该桥的MIDAS模型，分别计算主梁与桥塔在施工过程中位移值和成桥状态下活载位移值，再利用式（1）～式（6）计算主梁位移、桥塔位移和垂度效应产生的拉索导管梁端角度修正值，最后利用式（8）得到梁段预制时斜拉索的安装角度。

主桥斜拉索采用抗拉标准强度1 960 MPa的平行钢丝拉索，空间双索面体系，扇形布置，全桥共60对斜拉索。索梁锚固于边箱内，斜拉索于索塔内张拉。本文给出30对斜拉索的计算结果，如表1所示。其中M1～M15为在中跨布置的斜拉索，拉索M1为最靠近桥塔的拉索，其长度最短；而拉索M15为梁端锚点在跨中梁段上的拉索，索长最长；拉索M1～M15从桥塔到跨中依次布置，纵向布置间距为8 m。S1～S15为在边跨布置的斜拉索，拉索S1为最靠近桥塔的拉索；而拉索S15为梁端锚点在过渡墩附近梁段上的拉索；拉索S1～S15从桥塔到过渡墩依次布置，纵向布置间距为8 m。

表1 索导管角度修正量 （°）

从表1可以看出：在对拉索角度的修正值中，对于中跨布置的拉索M1～M15，拉索垂度效应产生的修正值最大，梁段预拱度和轴向角度产生的修正值次之，桥塔变形和固定支架变形产生的修正值最小；同时拉索长度越长，垂度效应的影响越大，索锚点所在梁段的预拱度会越大，索导管安装角度修正值也越大。对于边跨布置的拉索S1～S15，拉索垂度效应同样最为明显，但梁段预拱度产生的修正值较小，这是由于边跨梁段在支架上施工，对应的预拱度值较小；而梁轴向角度产生的修正值较大，这是由于边跨梁段处于直线段上，其角度几乎与线路竖向角度一致。因此，为了得到索导管安装角度的准确值，需计入上述不同因素对索导管安装角度的影响。

4 结论

（1）索导管安装角度修正是斜拉索施工的重要内容，应考虑影响安装角度的主要因素，包括拉索垂度效应、梁段预拱度、梁段轴向角度、桥塔变形及导管支架变形的影响。

（2）在这些影响因素中，拉索垂度效应产生的修正值最大，梁段预拱度和轴向角度产生的修正值次之，桥塔变形和支架变形的对应值最小。

（3）对于中跨索，拉索越长，垂度效应影响越大，梁段预拱度影响增加，索导管安装角度修正值也越大。

（4）对于边跨索，由于边跨梁段支撑较多，梁段预拱度产生的索导管角度修正值较小，但梁段轴向角度产生的修正值较大。