基于MiniSAT的命题极小模型计算方法

张 丽 王以松,2 谢仲涛 冯仁艳

1(贵州大学计算机科学与技术学院 贵阳 550025) 2(公共大数据国家重点实验室(贵州大学) 贵阳 550025) (gs.lizhang18@gzu.edu.cn)

命题可满足性问题(satisfiability problem, SAT)是计算机科学和人工智能研究的中心问题之一，在自动推理和人工智能等领域都具有非常重要的理论意义和实践价值，世界各国的相关研究人员在这方面做了大量的工作，提出了许多求解算法和大量的改进技术.

SAT问题的模型即为命题公式可满足时，使得命题公式可满足的一组真值指派中赋值为真的原子集合.当命题公式可满足时，极小模型的计算和验证问题就成了人们关注的重点问题.当命题公式不可满足时，人们通常对分析不可满足性感兴趣.极大可满足问题(maximum satisfiability problem, MaxSAT)[1-2]和极小不可满足子集(minimal unsatis-fiable subset, MUS)问题都属于这种分析.MaxSAT是SAT问题的优化版，其目标是找到一组真值指派使得CNF公式中满足(不满足)子句的数量极大化(极小化).随着MaxSAT技术的不断发展，MaxSAT问题在Android恶意软件检测[3]、排课[4]和诊断[5]等问题中都得到了很好的应用.MUS是SAT问题的扩展，是计算一个公式集的极小不可满足公式子集，其所有真子集均是可满足的.在现实中许多重要问题可以编码为MUS问题进行求解[6-8].

基于极小模型的推理一直是人工智能研究的重要主题[9-11].极小模型也是回答集程序设计(answer set programming, ASP)和其他非单调知识表示和推理范式的核心[12]，例如，限制逻辑[13-16]、缺省逻辑[17]、极小诊断[18-22].和稳定模型语义下的逻辑程序[23-24]等.极小模型主要涉及2个任务，对于一个给定的子句理论T，计算(任务1)：寻找极小模型即计算出T的一个极小模型；判定(任务2)：验证极小模型即检验给定的一个原子集是否是T的极小模型.

关于极小模型推理的研究结果表明，在一般情况下，这些问题是难以处理的.事实上，即使是正子句理论，计算其极小模型也是PNP[O(log n)]-hard[25].对于一个给定的理论，验证一个模型是否是其极小模型是co-NP-complete[26].关于极小模型求解这一问题的研究也吸引了一部分专家学者的注意，他们认为挑选出能够有效解决这些问题的各个理论是有意义的[27-29].目前计算子句理论的极小模型，可将子句理论转换成逻辑程序后用ASP求解器计算其回答集，ASP求解器的典型代表有clasp[30]，clingo[31]，DLV[32]等.

2016年Ben-Eliyahu-Zohary等人[33-34]提出了基于极小模型分解的计算极小模型的算法ModuMin和验证极小模型的算法CheckMin，使极小模型计算和验证的艰巨任务在原始理论的子集之间进行分解，把一个任务分解成多个子任务进行计算.但是该验证算法CheckMin并不可靠.

2020年王以松等人对这一问题展开了进一步的研究，提出了极小归约(minimal reduct, MR).极小归约是对Ben-Eliyahu-Zohary等人[33-34]的分解极小模型定理的补充，从而得到一个可靠的验证极小模型的算法CheckMinMR.

每年可满足性理论和应用方面的国际会议都会组织SAT竞赛，以求能够找到一组最快的SAT求解器.MiniSAT[35]是一个极简并开源的SAT求解器，赢得了2005年SAT竞赛的所有工业类别测试.MiniSAT的出现对于SAT问题的未来研究以及使用SAT的应用都是一个很好的起点.MiniSAT始于2003年，其目的是通过小型而高效的，并且提供有良好文档的SAT求解器来帮助人们进入SAT领域.其第1个版本只有600多行C语言代码，同时MiniSAT仍包含了2003年最新SAT求解的核心算法.在之后的版本中，代码量虽有所增长，但相较于其他的SAT求解器而言MiniSAT的代码量仍然非常小，为我们的代码实现提供了非常有利的基础.

本文的主要工作有3个部分：

1) 在MiniSAT求解器的最新版本MiniSAT2.2的基础上，对源代码进行修改实现了计算子句理论极小模型的算法MMSAT.

2) 将MMSAT算法与CheckMinMR算法结合成MRSAT实现快速极小模型的求解，将2个算法进行结合的目的是在验证一个模型是否是极小模型时，采用分解模型的思想将1个任务分解成多个子任务的方法来验证.即分解一个理论及其模型，当两者都变为空时，则意味着该模型确实是给定理论的极小模型.

3) 使用本文的2个算法对大量随机生成的子句理论以及SAT国际竞赛上的部分基准测试用例进行极小模型的计算；本文选择clingo作为评估标准，将所有测试用例分别转换成逻辑程序，使用clingo计算其回答集，clingo是目前计算逻辑程序回答集最有效的实现，它是gringo和clasp的组合；同时记录本文的2个算法计算极小模型使用的时间及clingo使用的时间.实验结果表明，本文提出的2个方法对随机子句理论和SAT竞赛工业测试用例十分有效，计算极小模型的速度都明显快于clingo.而且从在计算结果正确率上的表现来看，本文的2个方法也更加稳定.

1 预备知识

子句δ是由1个或多个文字通过逻辑或(∨)连接组成.子句理论Σ是由1组有限子句构成.SAT问题中的CNF公式由1个或多个子句通过逻辑与连接起来组成.若子句δ在模型M下为真，则称M满足δ，记为Mδ.

定义1.极小模型.给定一个命题公式Φ及其一个模型M，称M是Φ的极小模型，当且仅当不存在M′⊂M，使得Φ可满足.

一个析取逻辑程序P是由具有如下形式的规则构成的有限集合：

a1∨a2∨…∨am←am+1,am+2,…,an,
notan+1,notan+2,…,notal，

(1)

其中ai(1≤i≤l)是原子，a1∨a2∨…∨am表示该规则的头(head)，am+1,am+2,…,an,notan+1,notan+2,…,notal表示该规则的体(body).令r是形如式(1)的规则，记H(r)={a1,a2,…,am}，B+(r)={am+1,am+2,…,an}，B-(r)={an+1,an+2,…,al}，B(r)=B+(r)∪notB-(r)，通常将规则r表示成H(r)←B(r).令A(r)表示规则r中的原子的集合，A(P)表示逻辑程序P中原子的集合.当l=n时，规则r被称作是正规则，如果程序中所有规则都是正规则，则该程序为正程序.令M⊆A(P)，P关于M进行GL-归约的结果记为PM，PM={H(r)←B+(r)|r∈P,B-(r)∩M=∅}.若M是PM的极小模型，则称M就是P的稳定模型(也称为回答集).

一个子句δ可转换析取逻辑程序的规则r，且B-(r)=∅，即由CNF公式转换的逻辑程序为正程序.因为对正程序P，PM=P，故正程序的回答集就是其极小模型.

1.1 依赖图

令P是逻辑程序，P的依赖图(dependency graph)是一个有向图，记为GP=(V,E).GP的定义为：

1)P中的所有原子A(P)和子句δ都是GP中的节点；

2) 如果a∈B+(δ)，则对应的边e表示为(a,δ)；如果a∈H(δ)，则e表示为(δ,a)；

逻辑程序P的强依赖图SGP是由依赖图GP构造的有向无环图，对于GP中的每一个强连通组件，在SGP中都将其折叠成为一个节点.若GP中存在一条边e，在GP中是由强连通组件sc1中的一个节点指向强连通组件sc2中的节点；在SGP中这条边表示为由sc1指向sc2即可.一个有向图中入度为0的节点被称为源(source).若SGP中源中不包含原子，则称该源为空.

1.2 极小模型分解

CheckMin算法是Ben-Eliyahu-Zohary等人[33-34]提出对给定子句理论的一个模型进行验证，检验该模型是否为该子句理论的极小模型.

对于任意一个子句理论T，令X和Y为原子集合，且X∩Y=∅，则Reduce(T,X,Y)是将X在T中的原子全部赋值为真，Y在T中的原子全部赋值为假，从而得到约简的子句理论.

对于给定T的一个源S，TS表示在T中只包含S的子句集.

定理1.极小模型分解定理[33-34].给定一个子句理论T和T的一个模型M，令图G表示T的强依赖图SG，如果G中存在一个源S使得X=S∩M是TS的极小模型，令T′←Reduce(T,X,S-X)，则M-X是T′的极小模型.

根据定理1，Ben-Eliyahu-Zohary等人[33-34]提出CheckMin算法(算法1).然而Ben-Eliyahu-Zohary等人[33-34]提出的CheckMin算法并不是完备的，因此他们又提出了完备性的充分条件——模块化性质.

定义2.模块化性质.

1) 如果子句理论T的强依赖图SGT中只有一个强连通组件，则T的一个极小模型M相对于T具有模块化性质；

2) 给定一个子句理论T和T的一个模型M，如果T中存在源S使得X=S∩M是TS的一个极小模型，并且M-X是T′←Reduce(T,X,S-X)的极小模型，则M-X相对于T′具有模块化性质.

算法1.CheckMin(T,M).

输入：一个子句理论T、T的一个模型M;

输出：true或false.

①G←SGT;

② 迭代地删除G中所有为空的源;

③ whileG中存在源S，且S是TS的极小模型

do

④X←M∩S;

⑤M←M-X;

⑥T←Reduce(T,X,S-X);

⑦G←SGT;

⑧ 迭代地删除G中所有为空的源;

⑨ end while

⑩ ifM=∅ then return true;

如果T的极小模型M关于T具有模块化性质，则CheckMin(T,M)返回true.

1.3 极小归约

对于极小模型分解定理的不完备，王以松等人对此提出了极小归约，对极小模型分解定理进行补充.同时对算法CheckMin也进行了修改得到新的完备算法CheckMinMR(算法2).

算法2.CheckMinMR(T,M).

输入：一个子句理论T、T的一个模型M;

输出：true或false.

returnCheckMin(MR(T,M),M).

定义3.Minimal Reduct.给定一个逻辑程序P和原子集S，S⊆A(P)则P关于S的极小归约表示为MR(P,S)，MR(P,S)是正逻辑程序：

{H(r)∩S←B+(r)|r∈P,
B+(r)⊆S&B-(r)∩S=∅}.

(2)

从极小归约的定义可以得到一个非常明显的结论A(MR(P,S))⊆S.极小归约是根据闭区间假设来约简一个逻辑程序，即S中的原子被假定为真，而其它原子被假定为假.

引理1[35].令δ表示一条子句，M表示一个模型，有：

1)Mδ当且仅当MMR({δ},M)；

定理2.极小模型性质[35].令T是可满足的子句理论，且S⊆A(T)，则3种情况是等价的：

1)S是T的一个极小模型；

2)S是MR(T,S)的最小模型；

3)S={p|MR(T,S)p}.

2 计算极小模型的新方法MMSAT和MRSAT

本节将详细介绍本文提出的2个计算子句理论的极小模型算法，分别是基于SAT求解器的算法MMSAT和基于极小归约的算法MRSAT.

2.1 基于SAT的极小模型算法MMSAT

MMSAT算法的主要思想是：当子句理论T是可满足时，SAT求解器可计算出T的一个模型M；将该模型取反得到一子句∨M，并且将不属于M的其余原子也分别取反得到子句集将这些子句添加到T中得到一个新的子句集T′，再用SAT求解器迭代该过程计算.若M是T的极小模型，则新的子句集T′是不可满足的；反之，则说明M不是T的极小模型.根据这个思想我们设计出MMSAT算法(算法3).

算法3.MMSAT(T).

输入：一个子句理论T;

输出：T的一个极小模型M或无模型.

① ifT是不可满足的

② return无模型;

③ end if

④ whileT是可满足的do

⑤M←MiniSAT(T);

⑥T←T∪{∨M}∪

⑦ end while

⑧ returnM.

引理2.给定一个子句理论T及其一个模型M，M是T的极小模型当且仅当T∪{∨M}∪不可满足.

引理2显然成立.MMSAT算法(算法3)的行⑤计算T的一个模型，其while循环(行④～⑦)每次迭代生成的模型是其前一次生成的模型的真子集，因M是有穷的，故循环一定会在有限步内终止，引理2保证终止时计算出来的M是输入子句理论T的极小模型.

2.2 基于极小归约的极小模型算法MRSAT

MRSAT算法(算法4)是MMSAT与基于极小归约的极小模型验证算法CheckMinMR的结合.首先由MiniSAT计算子句理论的模型，然后由Check-MinMR检验计算出的模型是否是其极小模型.

下面的引理3可保证算法MRSAT的可靠性.

引理3.给定一个子句理论T，及其一个模型M，若M′⊆M，M′T，则MR(T′,M′)≡MR(T,M′)，其中T′=MR(T,M).

证明.

基始：当T=T′时，MR(T,M′)≡MR(T′,M′)成立.

步骤：令δ∈T，{δ′}=MR({δ},M)，由极小归约的定义可得MR({δ},M′)={H(δ)∩M′←B+(δ)|B+(δ)⊆M′}.MR({δ′},M′)=MR(MR({δ},M),M′)={H(δ)∩M∩M′←B+(δ)|B+(δ)⊆M′⊆M}.已知M′⊆M，综上可得MR({δ},M′)≡MR({δ′},M′).又因δ∈T，所以MR(T,M′)≡MR(T′,M′)，T′=MR(T,M).

证毕.

算法4.MRSAT(T).

输入：一个子句理论T;

输出：T的一个极小模型M或无模型.

① ifT是不可满足的

② return无模型;

③ end if

④ whileT是可满足的do

⑤M←MiniSAT(T);

⑥ ifCheckMinMR(MR(T,M),M)

⑦ returnM;

⑧ end if

⑨T←T∪{∨M}∪

3 实验结果与分析

我们在MiniSAT的基础上实现了算法3和算法4，在随机3CNF公式和SAT国际竞赛上的部分基准测试用例上进行了测试.在实验中我们使用的clingo是目前的最新版本clingo5.4(1)https://potassco.org，它是基化器gringo[36]和ASP求解器clasp的结合.本实验的工作环境是Linux5.1.11、8核3.50 GHz的CPU和32 GB内存.实验代码及数据地址：https://github.com/zhangli-hub123/minimal-model.

3.1 随机3CNF公式

实验中的3CNF公式是通过设置原子数量和子句数量随机生成的子句长度为3的CNF公式，其中原子数量n的范围设置为50～1 000，增幅为50；子句数量m的范围是3.0×n～5.0×n，增幅为0.1×n；对于其中的每种情况都分别有10个不同的3CNF文件，一个文件即一个CNF公式.我们使用MMSAT，MRSAT，clingo分别计算这些3CNF公式的极小模型，并统一设置计算时间上限为1 800 s.文件的计算结果的输出类型有可满足(SAT)、不可满足(UNSAT)和计算超时被终止(TO).我们按照输出类型分别统计了所有计算的平均结果.

图1～3分别展示了clingo，MMSAT，MRSAT计算随机3CNF公式的极小模型的平均CPU时间.如图1所示，clingo的峰值在原子数量为900，子句数量为3.8×900时，CPU时间为1 711 s;MMSAT和MRSAT在相同情况下的CPU时间分别为499 s和505 s.此时MMSAT用时最少，而clingo所用时间几乎是MMSAT和MRSAT的3倍.如图2和图3所示，MMSAT和MRSAT耗时最多的情况均是原子数量为800，子句数量为3.9×800，此时它们的CPU时间分别是760 s和758 s，而clingo在此情况下的CPU时间为842 s.此时也是clingo用时最长，而MRSAT用时最少.

Fig.1 The average CPU time of minimal model by clingo on random 3CNF formulas图1 clingo计算随机3CNF公式极小模型的平均CPU时间

Fig.2 The average CPU time of minimal model by MMSAT on andom 3CNF formulas图2 MMSAT计算随机3CNF公式极小模型的平均CPU时间

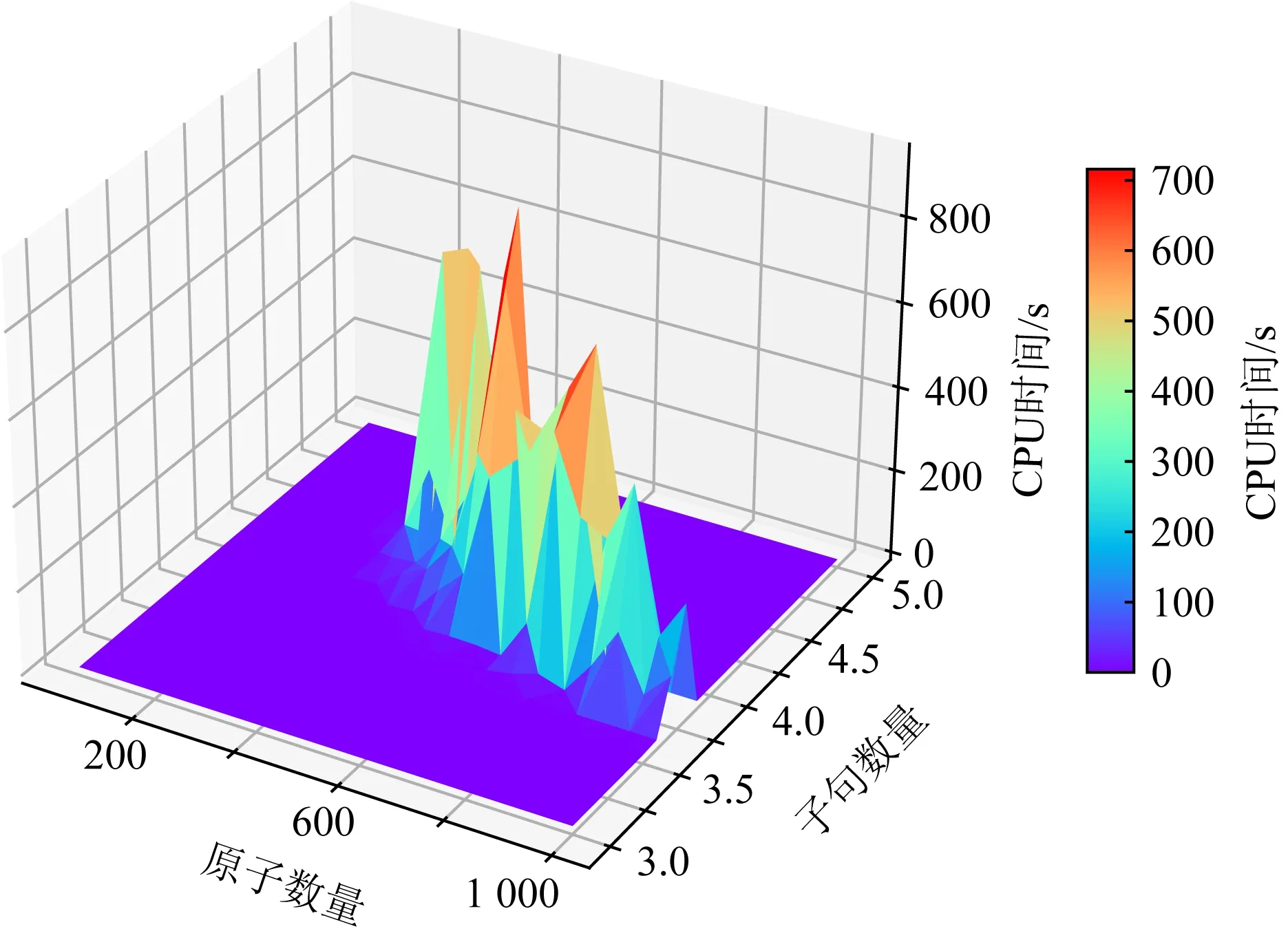
Fig.3 The average CPU time of minimal model by MRSAT on random 3CNF formulas图3 MRSAT计算随机3CNF公式极小模型的平均CPU时间

实验结果表明：计算随机3CNF公式的极小模型时，MMSAT和MRSAT在计算速度上的优势十分显著，从整体来看，几乎所有的情况下MMSAT和MRSAT的用时均比clingo少很多.而MMSAT和MRSAT之间则无十分明显的差别.

3.2 SAT竞赛基准测试实例

本实验所用的基准测试实例均获取自SAT国际竞赛，分别是2009年工业上的SAT实际测试用例(2)http://satcompetition.org/和2020年的测试实例(3)https://satcompetition.github.io/2020/downloads.html.我们从2009年的工业实例中随机挑选了7类实例，共计109个测试文件；从2020年的实例中随机选出43个实例，记为SAT2020，本文实验所用实例共计152个，即152个CNF公式.首先分别使用MMSAT，MRSAT计算所有测试实例的极小模型；并且以clingo5.4作为对比的基准程序，使用clingo5.4计算这些测试实例所对应的逻辑程序的回答集.由于clingo5.4在工业实例中出现了计算出错情况，因此我们在评估比较中加入gringo3.0.5+claspD1.1(其中gringo是claspD的前端).由于实例比较复杂，计算实例模型所需时间较长，并且本文算法是在计算模型的基础上更进一步计算极小模型，此时可能需要迭代多次，因此本实验将所有实例的计算时间上限设置为7 200 s.

如表1所示，我们对4种方法分别按照输出类型可满足(SAT)、不可满足(UNSAT)和超时(TO)统计了实例的计算结果(4)SAT，UNSAT，TO之外的其他实例均为内存不足.MRSAT在所有的实例类中均未出现内存不足..在规定时间内clingo和claspD计算完成(即输出类型为可满足或不可满足)的实例的数量均明显少于MMSAT和MRSAT，其中，clingo在bioinfo，c32sat，sat08实例类中共有11个实例发生了内存不足(而被killed)；在SAT2020中有8个实例发生了内存不足.gringo+claspD在c32sat中也有一个实例发生了内存不足(而出现std∷bad_alloc)；且在SAT2020中有8个实例发生了内存不足.MMSAT在SAT2020中有1个实例发生了内存不足(而出现INDETERMINATE).

值得注意的是，如表1所示，bioinfo实例类中clingo在规定时间内完成计算的实例数量为12，全部为不可满足.而MMSAT和MRSAT完成计算的实例数量均为20个，其中可满足的实例数量为9个，不可满足的为11个.通过对实验记录数据对比，我们发现在clingo计算的结果为不可满足的12个实例中，有7个实例在claspD，MMSAT，MRSAT中的结果都为可满足.表1中括号内的数字表示clingo计算出错(5)可满足的实例由clingo计算出的结果为不可满足.的实例个数.因此，我们将MMSAT和MRSAT计算的极小模型分别与文件中的子句进行了验证，验证结果均表明这7个实例确实是可满足的.同时，我们对所有测试实例的结果都进行了对比，在用例类sat08中和SAT2020也分别发现了一个实例为clingo计算出错的情况.

我们还统计了计算完成的实例的平均CPU执行时间，如图4所示.图4中MMSAT在crypto/md5gen实例类下计算极小模型的用时最多，除此之外，均是claspD完成计算的所需平均时间最长，其次便是clingo用时较长.整体来看MMSAT计算极小模型的平均时间最短，效果最好，MRSAT次之.对计算结果为可满足的实例的平均CPU执行时间我们也做了统计，如图5所示，在c32sat用例类下是MRSAT用时最多，在此实例类下clingo和claspD均没有算出实例的极小模型；其余均是claspD耗时较长，而MMSAT用时最短.

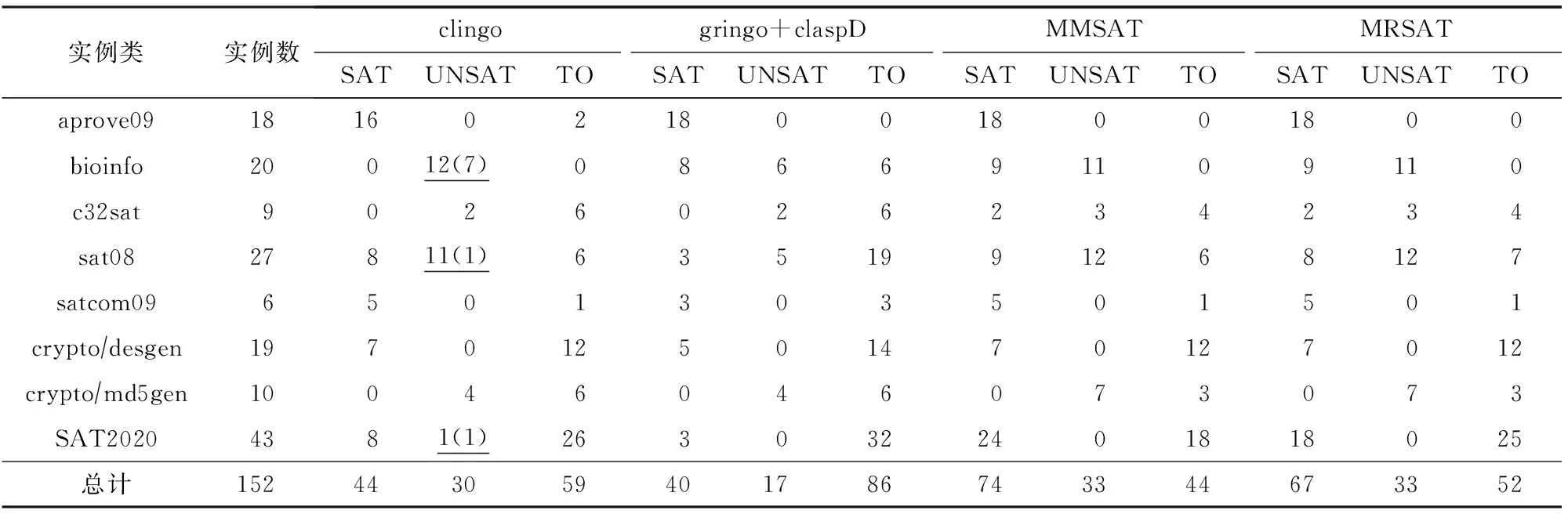
Table 1 The Results on Industrial SAT Benchmarks表1 计算SAT工业实例的结果对比

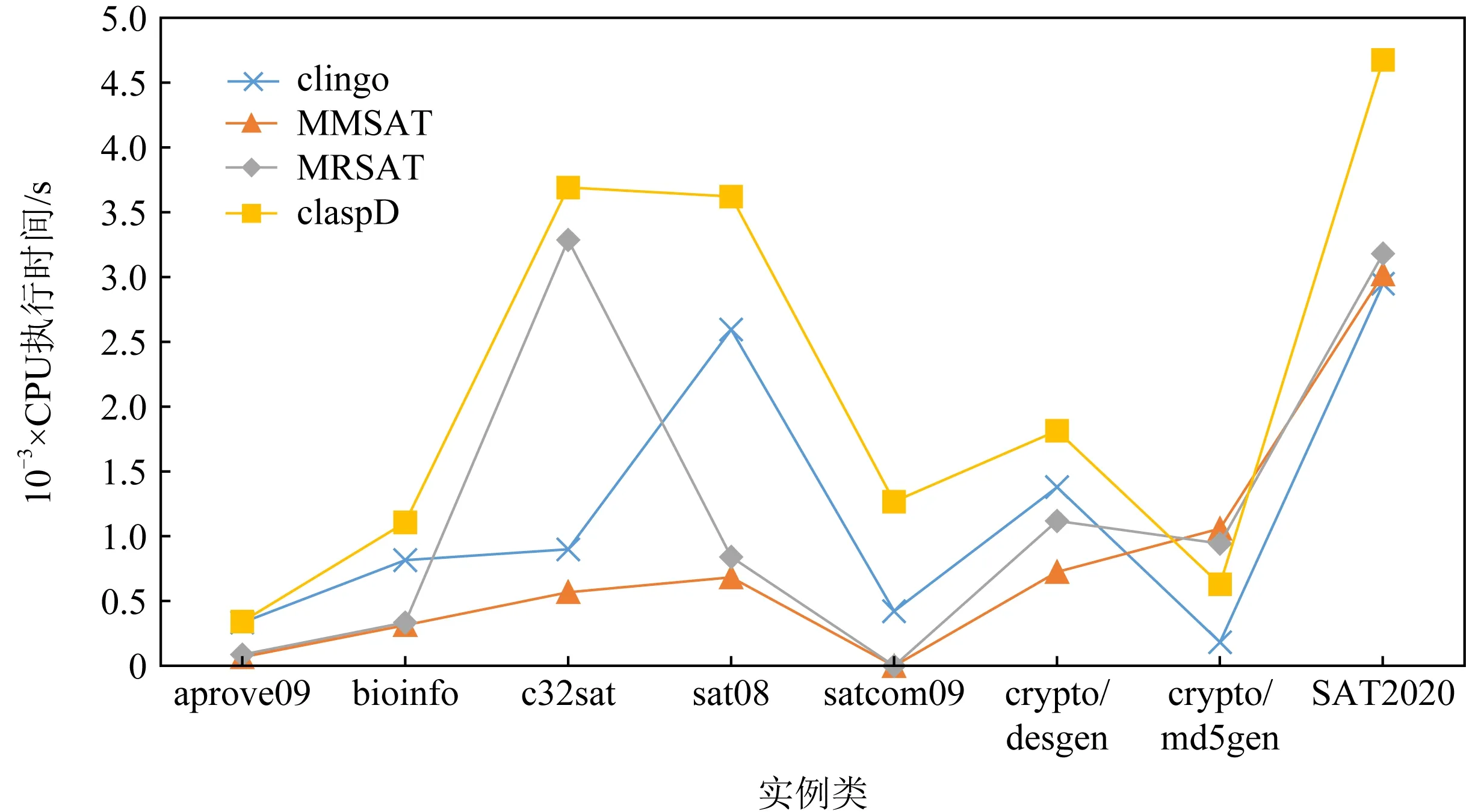
Fig.4 The average CPU time on industrial SAT benchmarks correctly completed图4 正确完成计算SAT工业实例平均CPU执行时间

Fig.5 The average CPU time of computing a minimal model on industrial SAT benchmarks图5 计算SAT工业实例极小模型的平均CPU执行时间

综上，在MiniSAT2.2基础上实现的计算极小模型的算法MMSAT和MRSAT是非常有效的，其计算极小模型的速度都明显快于最新版的clingo和claspD，并且clingo发生了计算错误，clingo和claspD均出现了内存不足，而我们提出的算法则更加稳定.

4 总 结

本文提出了基于SAT和基于极小归约的计算命题极小模型的算法MMSAT和MRSAT，首先证明了算法的可靠性，其次对算法进行了实现.最后，分别使用MMSAT，MRSAT，clingo5.4在随机3CNF公式和SAT国际竞赛上的工业实例上做了实验，在SAT国际竞赛上的工业实例上还使用gringo3.0.5+claspD1.1进行了测试.实验表明，使用MMSAT算法和MRSAT算法计算命题的极小模型，在时间上明显快于claspD和clingo，在正确率上也明显优于clingo.

在未来的工作中，根据分解极小模型的主要思想，在基于极小归约的算法MRSAT中可以做进一步的改进.通过采用并行计算的方式，使得对极小模型的验证更高效，从而提高极小模型计算的速度.此外，根据极小归约的性质，我们考虑将其直接应用在MMSAT算法中，将求解子句理论T的极小模型转化为求解极小归约之后子句理论的极小模型.我们将对这些问题做更进一步的研究.