一种满足差分隐私的轨迹数据安全存储和发布方法
2021-11-05吴万青赵永新底超凡
吴万青 赵永新 王 巧 底超凡
(河北大学网络空间安全与计算机学院 河北保定 071000) (河北省高可信信息系统重点实验室(河北大学) 河北保定 071000) (wuwanqing8888@126.com)
随着互联网的快速发展,许多电子设备融入现实生活,例如智能手机、智能手环等.但是在享受大数据便利的同时,也面临着隐私安全隐患.一些基于位置服务(location based services, LBS)应用软件在用户未知情的情况下,采集用户的地理位置信息并发布,不仅造成用户的位置隐私泄露,而且有可能造成更多的敏感信息泄露,如用户的生活习惯、宗教信仰等.据微软统计报告,有一半以上的用户担心自己在使用基于LBS的应用程序时泄露自己的隐私.因此在用户使用LBS时,如何实现位置轨迹数据的安全分享与发布,保护用户的个人隐私成为一个重要问题.
为解决位置隐私保护这一问题,国内外许多学者纷纷置身于此问题之中.2002年Sweeney等人提出K-匿名理论[1].文献[1]中定义了伪标识符和K-匿名性,广泛应用于轨迹匿名和隐私保护.2003年Gruteser等人将K-匿名的理论引入到位置隐私保护,提出一种空间位置隐藏方法[2].该方法的思想是通过空间隐藏方法隐藏单个用户与其他K-1个用户的地理位置使之无法区分,但是这种方法必须在特定情形下才能实现,所以用户不能根据自己的需求设置不同K值和需要隐藏的区域.2009年Chow等人提出一种个性化K-匿名模型[3],该方法是基于用户出现在隐藏区域相等的概率下提出的一种模型,但当用户出现的概率不等时,该模型不能很好地反映用户隐私的保护程度.
许多学者基于K-匿名模型,相继提出了K-匿名模型的变体.2006年Wang等人提出(X,Y)-匿名的概念,其中X,Y表示2个不相交的属性集合[4].该方法主要在处理敏感数据时增加了限制条件,在属性组X中属性相同的情况下,每一组X均需要对应至少K个不同敏感属性组Y中的值.2007年Zhang等人提出了(K,e)-匿名模型,目的处理敏感数值型数据,其思想为在每个等价类中元组个数不能低于K个,每个等价类中的敏感属性的取值范围不能低于给定的阈值e[5].Machanavajjhala等人在2007年提出l-多样化模型[6],这一方法是通过熵值定义数据的多样性及变化特征,要求在准标识符相同的情况下,敏感数据满足一定的多样化要求,保证了敏感数据的多样性,但是敏感数据如何分布该方法并未考虑.而t-贴近模型的提出解决了这一问题[7-8].t-贴近模型定义了一个阈值t,并要求等价类中敏感属性的分布和整个表的敏感属性分布的距离不能超过阈值t.
K-匿名模型优势在于攻击者能力不超过假设的前提下,能够以较小的代价保证同一等价类中记录的不可区分性,但当攻击者能力超过假设范畴,攻击者就可以进一步区分等价类中不同的记录,从而实现去匿名化,造成背景知识攻击.l-多样化模型虽然在一定程度上处理了K-匿名缺乏多样性的问题,但是该模型仍不能抵御概率推理攻击,若敏感属性分布不均匀时,导致实现该技术困难.t-贴近模型作为l-多样化模型的改进,解决了针对敏感属性的攻击,但是仍无法抵御背景知识的攻击,而且面对不同的敏感属性值时缺乏保护水平的灵活性.
因此,Dwork等人在2006年提出差分隐私技术,很好地解决了背景知识攻击及推理攻击的问题[9-10].该方法的主要思想是在数据库中添加噪声,达到攻击者无法识别其中任意一个数据是否在该数据库中.该技术是一种新的隐私保护技术,具有健强的数学基础,可以提供严谨的数学证明[11].差分隐私技术的提出,受到广大隐私保护领域研究者的关注,并广泛应用于支持隐私保护的数据挖掘和数据发布领域[12].2012年Andrés等人提出基于位置的差分隐私扩展模型,并生成一个在隐私预算范围内不会受攻击的匿名位置[13].但是由于生成的匿名位置与用户的真实位置之间的距离无法预测,所以不能保证LBS的服务质量.2013年Dewri等人利用Hilbert分布的匿名集获得高质量服务[14].但是匿名位置和真实位置没有相似性,攻击者很容易区分开.2018年Gursoy等人提出一种名为DP-Star的轨迹隐私保护框架[15].该框架构建了一个密度感知网络,可以确保添加噪声之后满足差分隐私的需求,保持数据的空间密度,并采用中值长度估计方法保护用户轨迹,生成了既保留了差分隐私性质又高效能地合成轨迹.2019年Deldar等人提出一种称为PDP-SAG的差分隐私机制[16],用于解决移动对象的非时空敏感属性,为了使添加噪声频率一致,对个性化差分隐私结构上的属性噪声值进行一致处理.
由于轨迹数据具有高维性,不仅包含时间戳信息,也包含位置信息.为了满足大量轨迹数据存储与发布,Chen等人在2012年首次提出将差分隐私应用于发布大量顺序数据的方案,采用一种基于混合粒度前缀树结构(SeqPT)存储轨迹数据[17].在节点计数中加入Laplace噪声,以确定子树是否能继续在相应的节点上继续增长,并利用前缀树的固有一致性约束性质进行约束推理.但是时间戳的增多导致树高也会增高,计算量随着树的高度增加而增加,而SeqPT模型并不适用于高维时空数据集.2018年Khalil等人提出一种加噪前缀树模型[18],并引入一种称为SafePath的算法,该算法引入可变高度和等级分类树改进了SeqPT,减少了空节点生成的可能性.虽然该算法提高了大型和稀疏数据集的效率,但是在处理真正的高维属性的时空数据时,不仅分类树会增加隐私预算,而且发布的轨迹数据集的可用性较低.2019年Zhao等人提出一种SR-树结构代替R树的最小外界矩形,Cons-SRT算法虽然抵御了非位置敏感信息攻击,但是由于树过高导致查询效率下降[19].
为此,为了处理树高的增加导致查询效率下降的问题,本文提出一种基于差分隐私的噪声前缀树结构应用于轨迹数据的存储与发布.本文首先通过轨迹的时间特性以及速度和方向的特征,划分出不同时间戳的轨迹等价类.其次采用Hilbert曲线对各个轨迹等价类中的位置点进行标号划分,并计算每个等价类的中心点.然后由前缀树的节点存储该中心点,根据移动用户的轨迹特征,从而获取轨迹的时空特性,保证了轨迹数据的存储与发布.最后利用差分隐私技术对节点存储的敏感数据添加噪声.
本文的贡献有3个方面:
1) 不仅考虑轨迹的时间特性,而且通过计算轨迹间的速度距离和方向距离构建轨迹等价类,并提出一种满足差分隐私性质的轨迹数据发布算法.为防止攻击者通过轨迹背景知识和上下文信息获得隐私数据,本文采用差分隐私技术对敏感数据进行加噪.
2) 证明本文提出的隐私保护方案满足差分隐私性质,并进一步降低了轨迹数据的时间复杂度.
3) 使用真实的数据库进行试验,评测本文提出方案的效率和效用.证明文本的方案使得合并轨迹时间更少,并确保轨迹数据的可用性.
1 问题陈述
1.1 轨迹概念
定义1.轨迹.轨迹是指移动对象经过的一系列二维时空点的集合:
T={id,(l1,t1),(l2,t2),…,(l|T|,t|T|)},
(1)
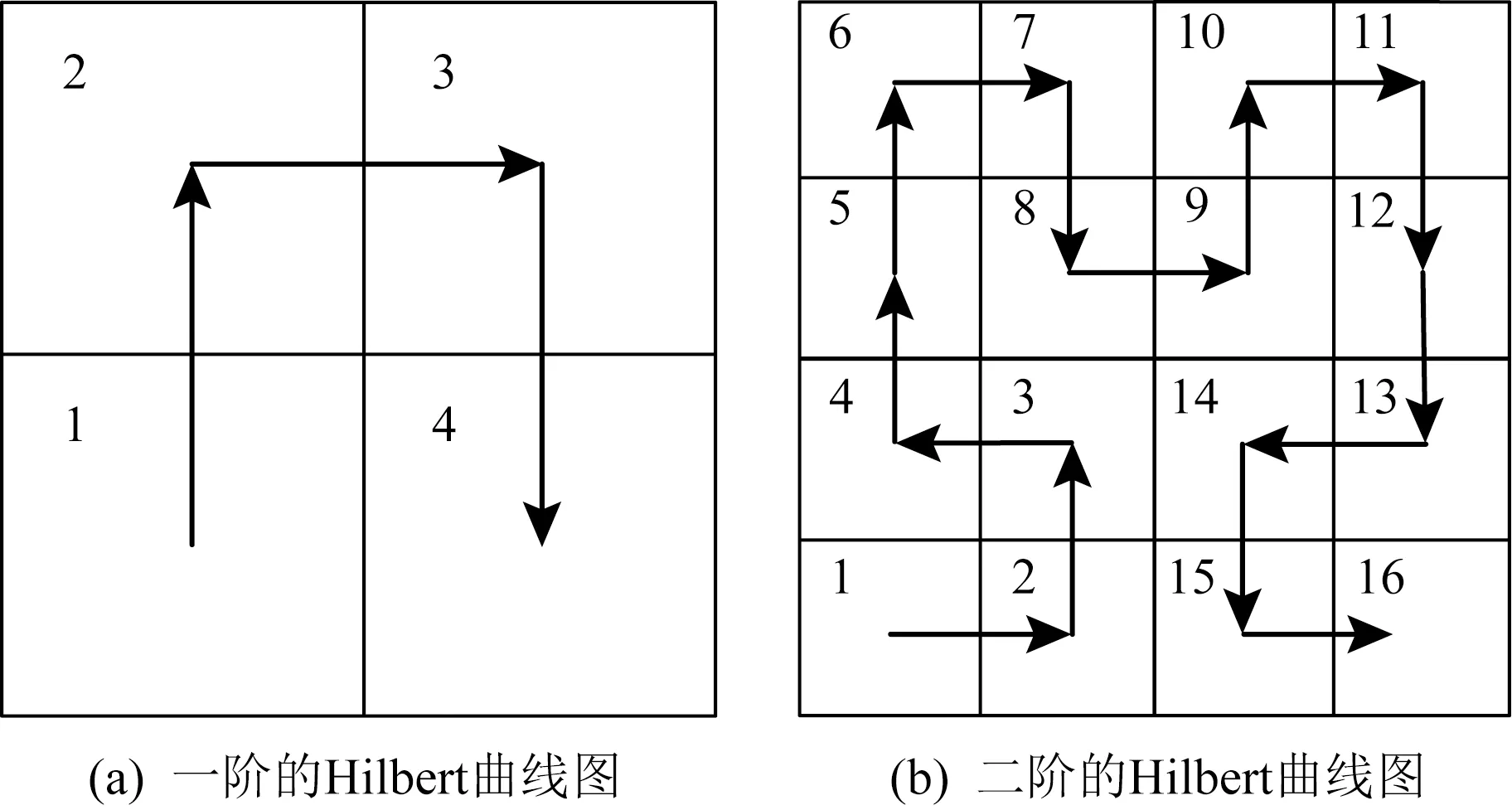
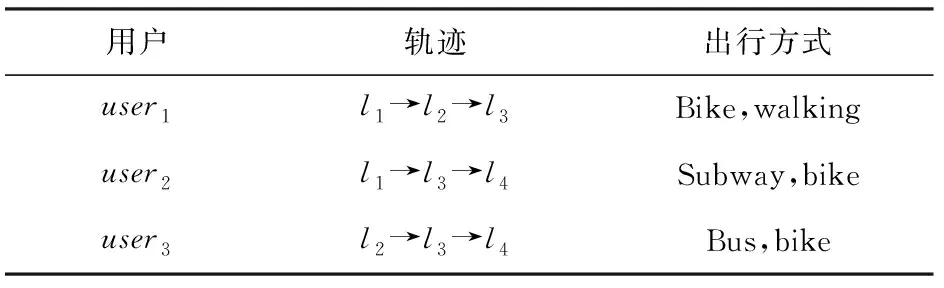
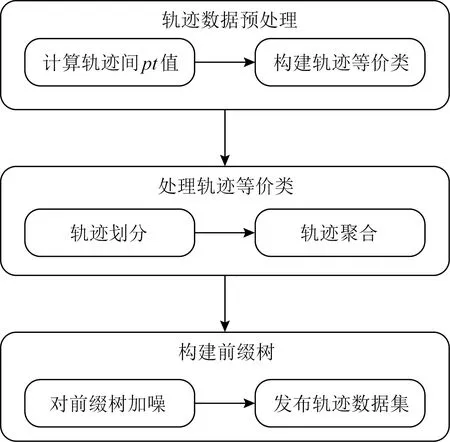
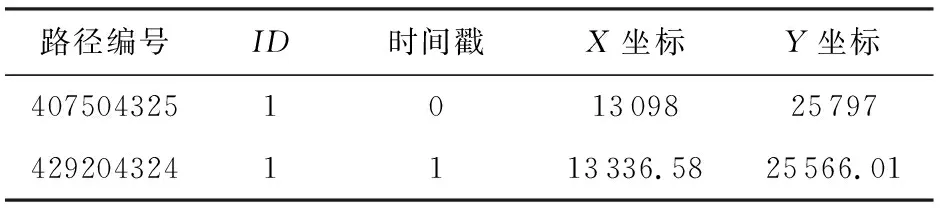
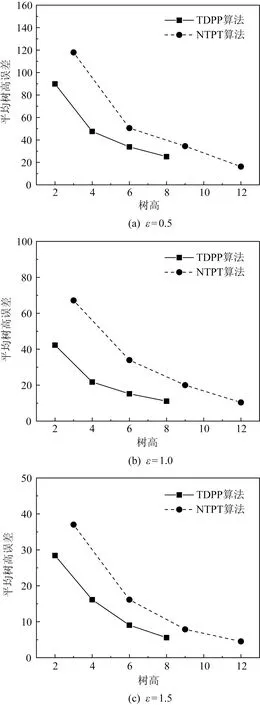
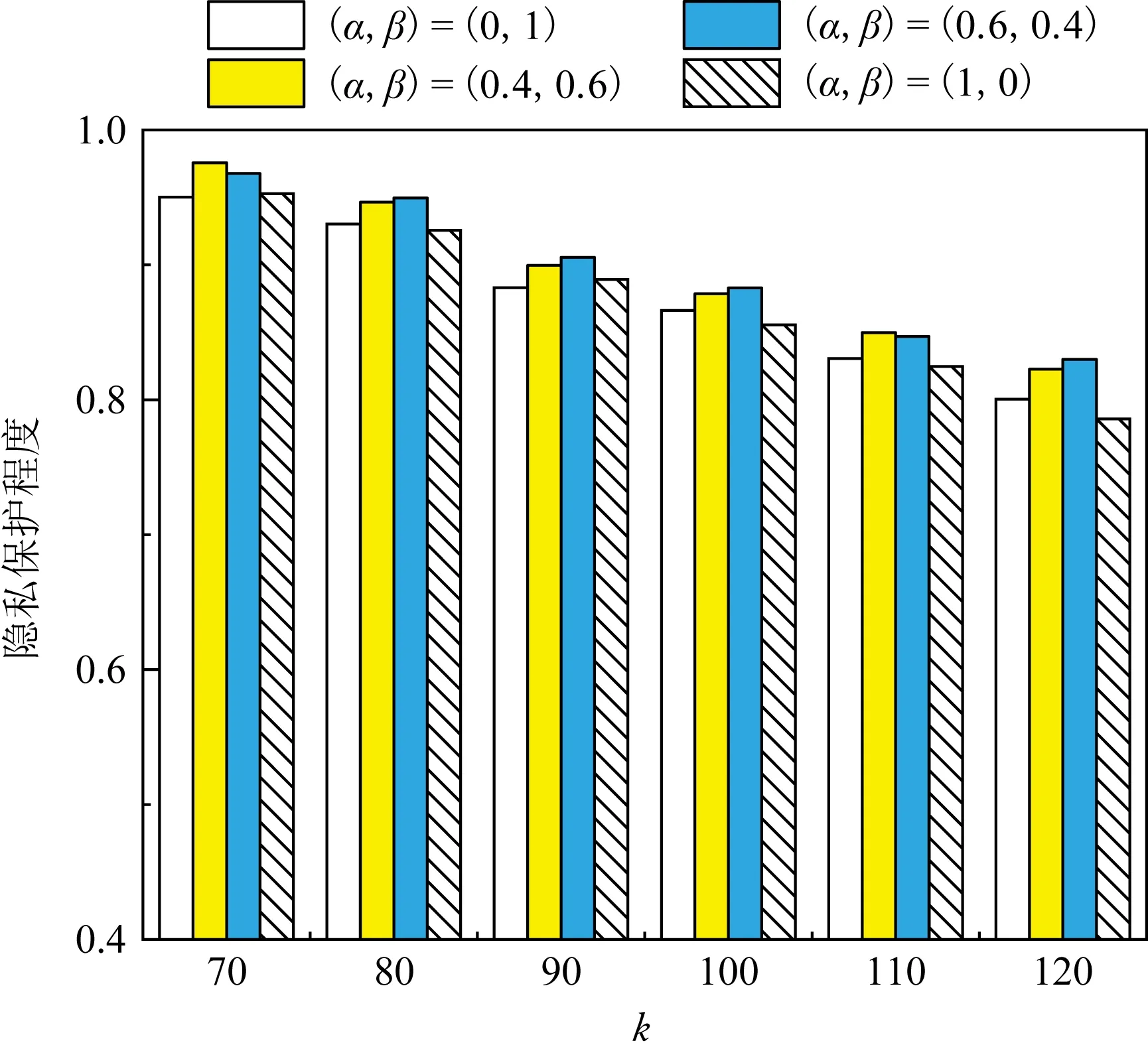
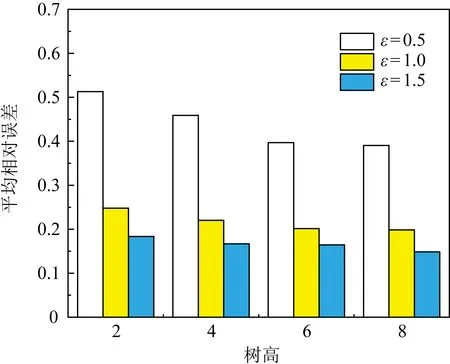
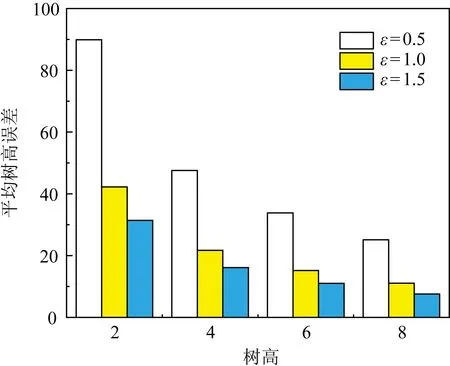
其中,|T|为轨迹轨迹中位置点个数,即轨迹的长度,t1 多条轨迹Ti构成的集合为轨迹集D,表示为D={T1,T2,…,Tn}. (2) 当pt=0时,轨迹Ti和Tj不是同步轨迹;当pt=100时,轨迹Ti和Tj具有相同的起始和结束时间.我们定义time(Ti,Tj)表示2条轨迹的重叠时间戳,即: (3) 定义4.轨迹等价类距离矩阵TDM.轨迹等价类距离矩阵为n阶对称矩阵 (4) 其中,dij表示轨迹Ti和Tj的距离. 定义5.离散Fréchet距离[21].设2条曲线A={a1,a2,…,am},B={b1,b2,…,bn}由多个离散位置点点组成,则2条曲线的序列组合可以表示为L={(a1,b1),(a2,b2),…(am,bn)},定义L为所有序列对中最大距离.则离散Fréchet距离可以表示为 (5) 定义6.轨迹方向距离[20].2条轨迹Ti和Tj满足pt>0,我们用disto(Ti,Tj)表示这2条轨迹的方向距离,即: (6) 定义7.轨迹速度距离[20].2条轨迹Ti和Tj满足pt>0,我们用distv(Ti,Tj)表示这2条轨迹的速度距离,即: (7) 定义8.轨迹距离.2条轨迹∀Ti,Tj∈D,D为轨迹数据集.当2条轨迹Ti和Tj满足pt>0,那么轨迹间距离Dist(Ti,Tj)定义为 Dist(Ti,Tj)=δdF(Ti,Tj)+ 其中,disto(Ti,Tj),distv(Ti,Tj)分别由式(6)和式(7)所得,α和β分别代表方向距离和速度距离的权重值,满足α,β∈[0,1],α+β=1. 定义9.ε-差分隐私[12].给定数据集D和其相邻数据集D′(2个数据集中最多相差一条记录),函数f的任意输出S满足: Pr[f(D)=S]≤Pr[f(D′)=S]×eε, (8) 则称函数f满足ε-差分隐私,其中隐私预算ε>0. 隐私预算ε表示隐私保护程度,由数据拥有者指定.ε越大,数据可用性越大,提供的隐私保护程度越低;ε越小,数据可用性越小,提供的隐私保护程度越高、相邻数据集D和D′查询结果的概率分布越相似,攻击者更难以判断数据集中的某一元素. 定义10.全局敏感度[22].设2个相邻数据集D和D′至多相差一条记录,函数f:D→Rd的全局敏感度: (9) 其中,R表示映射空间,d表示函数f输出的维度.全局敏感度直接影响噪声添加量,在相同的预算ε下,函数f的全局敏感度越大,添加的噪声越多,导致数据可用性降低. 定义11.拉普拉斯机制[9].设查询函数f:D→Rd满足ε-差分隐私机制,对函数f的输出添加拉普拉斯噪声,即 (10) 其中,算法A提供ε-差分隐私保护.产生拉普拉斯噪声机制的密度函数为 (11) 定义12.序列组合性[23].给定一个数据集D和n个函数f1,f2,…,fn,每个函数fi(1≤i≤n)满足εi-差分隐私,则函数组合F(f1(D1),f2(D2),…,fn(Dn))满足∑εi-差分隐私.对于 必有: (12) 定义13.并行组合性[23].假设Di(1≤i≤n),是原始数据集D中彼此不相交的子集,对每个子集Di作用一个差分隐私函数fi,其隐私保护参数为εi,函数组合F(f1(D1),f2(D2),…,fn(Dn))提供(maxεi)-差分隐私保护.则称函数fi在D上的并行组合满足(maxεi)-差分隐私. 前缀树[17]是哈希树的一种变体结构,通过对每一层节点进行遍历,减少不必要的节点比较,从而提高检索效率. 定义14.前缀树.一个前缀树PT的结构可以被定义为PT=(Root,E,V),其中Root表示前缀树PT的虚拟根且Root(PT)∈V;E代表前缀树节点之间边的集合;V表示前缀树节点的集合且v∈V.前缀树中的节点存储聚合后的轨迹位置点,在前缀树上同一个父节点下的所有轨迹序列都有相同的前缀. 定义15.Hilbert曲线.Hilbert空间填充曲线是一种无限迂回发展的空间填充曲线[24],空间填充曲线是指用一条连续的曲线填满一个封闭的区域. 图1分别展示了一阶、二阶的Hilbert曲线图: Fig.1 Hilbert curve图1 Hilbert曲线图 定义16.背景知识和上下文敏感信息攻击.背景知识通常是关于特定用户或数据集的相关信息.在一些文献中如文献[25]提出的攻击模型大多属于背景知识攻击的范畴,背景知识又称查询记录链接攻击. 表1中给出3个用户user1,user2,user3的活动轨迹以及出行方式,假设攻击者通过观察得到其中一用户的出行方式Subway,然后与数据集中的记录建立连接,可得知该用户user2的出行方式符合条件,从而也可以得到user2的轨迹以及其他相关的敏感信息. Table 1 The Information of Users 2.1节介绍原始轨迹数据的预处理;2.2节介绍Hilbert曲线处理轨迹等价类;2.3节提出一个加噪前缀树的存储结构;2.4节介绍基于前缀树的差分隐私保护算法;2.5节介绍了数据的查询过程;2.6节对提出的算法进行分析.其算法流程图见图2. Fig.2 Flowchart of trajectory data publishing algorithm图2 轨迹数据发布算法流程图 在数据预处理阶段,本文需要完成2个步骤: 1) 识别轨迹的起始时间和终止时间.在轨迹数据集中,我们需要识别每条轨迹的起始时间和终止时间来构造轨迹等价类.本文我们设定一个时间阈值Δt作为时间间隔,并规定在该阈值中的轨迹都视为同一个轨迹等价类.例如,设置阈值Δt为10 min,当且仅当起始时间为[9:00,9:10],终止时间为[10:00,10:10]的所有轨迹视为同一个轨迹等价类.因此存在轨迹等价类中的轨迹满足pt>0. 2) 构建轨迹等价类.为保证在相同时间段中的轨迹能够得到隐私保护,本文采用构建轨迹等价类方法,将第一步中的轨迹匿名在同一个匿名集中.考虑到实际场景中,为了减少轨迹数据的损失,可以适当将时间阈值Δt扩大,保证所有的轨迹得到匿名保护. 算法1描述了轨迹数据预处理过程. 算法1.轨迹数据预处理. 输入:原始轨迹数据集D={T1,T2,…,T|D|},Δt; 输出:轨迹等价类EC、轨迹等价类距离矩阵TDM、轨迹时间重叠率矩阵PT. ①EC=∅,TDM,PT为空矩阵; ② for eachTi∈D ③ ifTi的开始和结束时间在规定范围内 then ④Ti存入EC,EC={T1,T2,…,Tp} (p≤n); ⑤ end if ⑥ end for ⑦ forTi,Tj∈EC,i=1:p ⑧ forj=i+1:p ⑨ 利用式(1)和式(6)计算Ti和Tj的pt值及距离Dist(Ti,Tj); ⑩pti,i=tdmi,i=0; 算法1的行①~⑥为构建轨迹等价类,此过程仅判断每条轨迹是否在规定的范围内,轨迹数据集中有n条轨迹,则需要判断n次,因此可以在时间O(n)内完成.行⑦~为构建轨迹等价类的距离矩阵,构造距离矩阵需要计算n(n-1)/2次轨迹间的距离,则此过程可以在时间O(n2)内完成.因此算法1的完成时间在O(n2)内.由于存储到矩阵TDM和PT中,因此空间复杂度为O(n2). 算法2描述了算法1中行⑨求轨迹间距离Dist(Ti,Tj). 算法2.多特征轨迹距离算法(multi-feature trajectory distance algorithm). 输入:等价类EC的任意2条轨迹P和Q,P={(x1,y1),(x2,y2),…,(xp,yp)},Q={(x1,y1),(x2,y2),…,(xq,yq)},轨迹时间同步率矩阵PT、方向距离权重α和速度距离权重β; 输出:Dist(P,Q). ①δdF(P,Q)=disto(P,Q)=distv(P,Q)=∅; ② 初始化一个p×q矩阵的矩阵C,其元素初始值均为-1; ③ fori=1 top ④ forj=1 toq ⑤ ifci,j>-1 ⑥ returnci,j; ⑦ else ifi==0&&j==0 ⑧δdF(P,Q)=Euclid(P,Q); ⑨ else ifi>0&&j==0 ⑩ 递归计算ci-1,j的值,δdF(P,Q)= max(ci-1,j,Euclid(P,Q)); max(ci,j-1,Euclid(P,Q)); δdF(P,Q)=max(min(ci-1,j, ci-1,j-1,ci,j-1),Euclid(P,Q)); disto(P,Q); distv(P,Q); Dist(P,Q)=δdF(P,Q)+ α×disto(P,Q)+β×distv(P,Q); 通过算法1和算法2完成对轨迹等价类的构建.2.2节介绍轨迹等价类的处理过程. 2.2.1 Hilbert曲线轨迹的划分 1) 通过计算轨迹之间的pt值和轨迹之间的距离Dist(Ti,Tj),将原始数据集D划分成不同的轨迹等价类ECi.根据每个等价类ECi位置点集Li,计算各个位置点集Li的Hilbert曲线阶数order. 算法3.轨迹划分算法(DPRD). 输入:等价类ECi、位置点集合L={L1,L2,…,L|T|}、总隐私预算ε、划分区域子集中k个位置点; ② 由轨迹等价类ECi得到每个位置点集Li; ④ for each 位置点集Li ⑥ end for ⑦ 生成n条Hilbert曲线; ⑧ for each Hilbert curve 2.2.2 轨迹的聚合 算法4.轨迹的聚合过程(TPOP). ④ for eachT∈D ⑤ for eachLi∈EC ⑦ end for ⑨ end for ⑩ end for 前缀树是一种可以用来存储大量字符串的树形结构[17],它的优点可以利用字符串的公共前缀来节省存储空间,最大限度地减少无谓的字符串比较,提高数据的查询效率.本节主要介绍前缀树存储轨迹数据的操作步骤: 2) 选择合适的节点.向前缀树中插入一条新轨迹时,首先从根节点开始向下遍历,比较要插入轨迹的第1个轨迹点,确定该轨迹点是否存在于第2层的节点中,如果存在就继续向下遍历下一层,直到遍历到某个节点没有相同前缀的位置点,则在当前节点vi下生成新的子节点vi+1存储轨迹数据.如果第1个位置点不存在前缀树中,则生成根节点的子节点,将轨迹的第1个位置点存入到该节点中,然后继续创建新的节点,将剩下所有的轨迹点依次存入新创建的节点中.最后对所有的位置点做步骤2)中相同的操作,直至所有的位置点存入到前缀树中. 3) 更新父节点.在前缀树中,如果子节点中不存在要存入轨迹的第1个位置点,则不需要更新除根节点以外其他节点信息.若插入的轨迹与前缀树上节点存储的轨迹有相同的前缀,则需要更新根节点和当前路径上的所有节点的信息,用于计数通过位置点的所有移动对象. 介绍一个构造前缀树的例子,如图3所示: Fig.3 Prefix tree图3 前缀树 Fig.4 Insert a new trajectory in the prefix tree图4 在前缀树中插入一条新的轨迹 Fig.5 Insert a new trajectory in the prefix tree图5 在前缀树中插入一条新的轨迹 通过遍历整个前缀树可以获得每条轨迹路径以及路径上移动对象的数量,并能判断出某个区域的密集程度和一些上下文非位置敏感信息.同时考虑到轨迹在时间和空间上的特性,若攻击者采取背景知识攻击和推理连接攻击,很容易获得移动对象的敏感信息,造成隐私泄露.为保证新轨迹的发布质量和可用性,我们使用前缀树结构存储轨迹数据,然后利用差分隐私技术对新轨迹位置点上的原始轨迹数、移动对象的数量等信息添加噪声,用于保护轨迹数据的隐私性. 算法5.基于前缀树的差分隐私保护算法(TDPP). ① 创建一个高度为h的前缀树PT; ③ fori≤h ⑤θi=k×i-1+b; ⑥ for 每一个节点vi的孩子节点vi+1 ⑧ ifvi+1.count≤θithen ⑨ 节点vi+1存入到前缀树PT中; ⑩sum=sum+vi+1.count; 除根节点外,前缀树的每个节点存储一个位置点,从根节点的子节点到叶子节点的路径构成一条轨迹,因此加噪前缀树支持对轨迹路径的查询.其查询的具体过程步骤为: 1) 从根节点开始向下访问包含轨迹位置点的所有节点.取出要查询轨迹的第1个位置点,然后检索前缀树中根节点的子节点是否存储该位置点.如果该位置点存在,则将节点中的移动对象的噪声计数值添加到查询结果中.如果查询的位置点不存在节点中,则查询结束. 2) 将要查询的位置点依次取出,然后根据步骤1)依次检索位置点是否存在前缀树的节点中,并将移动对象的噪声计数值添加到查询结果中.直至全部位置点检索完成. 3) 返回所有的查询结果和计数值总和. Fig.6 The query process of the prefix tree图6 前缀树的查询过程 本节我们对提出的模型进行隐私性分析和数据可用性分析. 2.6.1 隐私性分析 轨迹隐私保护的衡量标准是通过攻击者能在发布轨迹集中识别出该轨迹概率的大小.为此我们证明所提出的方案满足差分隐私性质. 引理1.轨迹区域划分算法(TRD)在整个轨迹数据集上可以保证|T|×ε-差分隐私. (13) 根据引理1,我们得到定理1. 定理1.整个方案过程消耗的隐私预算小于等于ε,即ε=εe+εl,本文方案满足ε-差分隐私保护. 2.6.2 数据的可用性 本文中的数据可用性分析主要分2个阶段:轨迹预处理阶段以及轨迹数据存储到前缀树.因此在轨迹预处理阶段中,我们将信息丢失率DOP作为本文衡量数据可用性的标准.当删除的轨迹数据占等价类中轨迹总数的比值越小,说明数据可用性越高,即: (14) 其中,nEC表示等价类的数量,mi为每个等价类中所要删除的轨迹数量. 在轨迹数据存储到前缀树阶段中,我们引入定义17和18作为数据可用性的衡量标准,在保证数据隐私性的情况下,相对误差和平均树高误差越低,则说明数据的可用性越高. 定义17.相对误差.对于计数查询Q,本文采用相对误差衡量加噪后发布的数据集D′对比于原始数据集D中数据的可利用率[26]: (15) 其中,thr是一个阈值,用于防止在极小计数查询的情况下,分母为0,即Q(D)=0. 定义18.平均树高误差.对于计数查询Q,本文采用平均树高误差衡量隐私保护后的数据集D′对比于原始数据集D中数据的可用性[27]: (16) 本文采用微软研究院发布的T-Drives数据库[28],该数据集包含一周内10 357辆出租车的轨迹,总位置点约为480万个.表2为数据集D部分数据的格式,其中路径编号为移动对象的不同的轨迹,ID为移动对象的标识符,时间戳用于构建轨迹等价类.为验证本文算法的隐私性和数据的可用性,与Zhao等人提出的NTPT算法[27]进行对照实验. Table 2 Partial Data Format of Dataset 本文的实验环境为Window10,Intel®Xeon®Silver 4214R @ 3.00 GHz,32 GB内存,采用Python和Jupyter NoteBook. 在轨迹预处理部分,本文引入了轨迹的时间特性以及轨迹间的速度距离v和方向距离o,通过计算其轨迹间的距离值,将原始轨迹数据集D划分成多个时间戳不同的轨迹等价类. 图7中展示了方向距离的参数α和速度距离参数β分别为(0,1),(0.4,0.6),(0.6,0.4),(1,0)随着k值增大,信息丢失率的变化趋势.从图7可以看出,在相同的k值下,(α,β)=(0,1)或(1,0)的信息丢失率较高于(α,β)=(0.4,0.6)或(0.6,0.4).因为当其中一个参数为0时,其约束条件减少,导致计算轨迹间的相似程度误差较大,因此在使用Hilbert曲线划分轨迹等价类时,会产生较高的误差,造成数据可用性降低.同样,随着k值的增加,信息丢失率也随之增高,因为k值越大,轨迹间的相似程度偏差越大,数据可用性越低.因此,本文实验中取参数(α,β)=(0.4,0.6)以及k=70. Fig.7 Data loss rate under different parameters (α,β)图7 不同参数(α,β)的数据丢失程度 3.1.1 隐私预算对误差的影响 在不同的隐私预算下,根据不同的查询长度我们进行2组实验,查询长度|Q|分别取值4和8.为了保证实验数据的真实性,每组查询对象都是从树存储结构中取得,每组实验测100次,且每组实验中添加噪声方式与Zhao等人[28]一致并具有随机性,最后取得100次结果的平均值做为最终结果. 图8中分别给出了查询长度为4和8的平均相对误差.从图8(a)和(b)可以看出,在相同的查询长度下,平均相对误差随着隐私预算的增加而减小.这是因为每一层节点的噪声量随着隐私预算的增加而减小,所以数据量的相对误差也随之减小.同样,从实验图中可以看出平均相对误差随着查询长度的增加而减小,因为随着查询长度的增加,导致树高也在增加,叶子节点中的噪声量随着阈值的限制而减小,因此平均相对误差也逐渐减小. Fig.8 The effect of privacy budget on the average relative error under different query length Q图8 查询长度Q不同时隐私预算对平均相对误差的影响 通过实验结果我们可以得出,在相同的隐私预算下,本文的TDPP算法在平均相对误差上较低于NTPT算法. 3.1.2 树高对误差的影响 本组实验测试了树高的变化在不同隐私预算下对平均误差的影响.根据本文的实验数据和隐私预算的大小,我们设置了3组实验.由于本实验前缀树中存储的轨迹最长长度为9,所以树的高度为9.因此在相同的隐私预算下,每组实验中的树高取2,4,6,8,并测得每个树高所对应的树高误差值.每组实验测试100次,取平均树高误差作为最终结果. 如图9(a)~(c),实验表明平均树高误差随着树高的增加而减小.因为隐私预算随前缀树的高度增加而减小,所以叶子节点中的噪声量也会随之减少.对比3组实验,平均树高误差随着隐私预算的增加而减小,因为隐私预算的增加导致噪声量的添加减小,所测得平均树高误差也相应减小.从图9可以看出本文方案的平均树高误差同样较低于NTPT算法. Fig.9 The effect of height on the average height error under different ε图9 树高对平均树高误差影响 因此,本文提出的TDPP算法不仅在平均相对误差值上较低于NTPT算法,同样在平均树高误差值上也较低于NTPT算法.因此可以证明出本文的TDPP算法的数据可用性较优于NTPT算法. 本文方案在轨迹预处理阶段,由于轨迹的时空特性,因此在时间和空间上对轨迹划分成多个轨迹等价类.考虑到在计算轨迹之间的距离时,参数的改变会影响隐私保护程度,因此在图10中给出了本文算法在不同的k值下,隐私保护程度在方向距离的参数α和速度距离参数β分别为(0,1),(0.4,0.6),(0.6,0.4),(1,0)时的变化趋势. Fig.10 Privacy protection level under different parameters (α,β)图10 不同参数(α,β)下的隐私保护程度 如图10所示,隐私保护程度随着k值的增高而降低,因为聚类的轨迹数量越多,数据的可用性也就越高,但隐私保护程度随之下降.当参数α,β为(0,1)和(1,0)时,隐私保护程度较低于参数为(0.4,0.6),(0.6,0.4)时的情况,因为参数为0时,轨迹之间减少一个约束条件,导致轨迹间的相似度下降,攻击者越容易识别出其中某个轨迹,故隐私保护程度也会随之降低.当参数α,β为(0.4,0.6),(0.6,0.4)时,隐私保护程度接近,因为根据不同用户的保护需求,所提供的不同的隐私保护水平,但在总体上的隐私保护程度是接近一致的. 因此,本文方案不仅考虑了数据的可用性,同时也保证了数据的隐私性.综上,参数(α,β)取值(0.4,0.6),k取值70. 为保证轨迹数据的安全性和可控性,本文采用差分隐私技术,并将Laplace噪声添加到存储轨迹位置点的节点中.本组实验测试了不同的树高在不同的隐私预算下对平均相对误差和平均树高误差的影响.图11的实验测试树高的变化对平均相对误差的影响,图12的实验测试树高的变化对平均树高误差的影响.从这2组实验中可以看出,平均相对误差和平均树高误差随着树高的增加而减小,随着隐私预算的增加也减小.因此,控制隐私预算的合理分配不仅可以保证轨迹数据的可用性,也能保证数据的隐私性. Fig.11 The average relative error of different privacy budgets图11 不同隐私预算的平均相对误差 Fig.12 The average height error of different privacy budgets图12 不同隐私预算的平均树高误差 随着人们进入大数据时代,位置感知设备在日常生活中发挥重要作用,它主要通过收集用户的位置信息提供高质量服务,但其中可能也包含大量的敏感信息数据.针对该问题,本文提出一种基于差分隐私的轨迹数据发布方法.根据轨迹大数据的特性以及轨迹路径的特点,本文提出一种基于前缀树的存储结构用于存储划分后的轨迹位置点,然后利用TDPP算法对节点中的敏感数据添加噪声,用于保护轨迹数据隐私.最后,本文在真实数据集上进行了数据可用性和隐私性的实验,并与NTPT算法进行对照实验,结果表明,本文算法具有较低的平均相对误差和平均树高误差,优于NTPT算法. 隐私保护是当前社会局势的一个热门领域,其中对轨迹数据的隐私保护是一个具有重要意义的研究方向.如今越来越多的“可信”第三方数据收集者并不可信,甚至一些基于位置服务的软件在用户不知情的情况下有意或无意地泄露用户的原始数据,造成大量的数据隐私泄露.考虑轨迹数据的特点,今后的研究工作可以主要针对3个方面:1)数据量大,构建存储结构应考虑遍历快,减少存储空间等特性.2)提高数据的可用性,可减少噪声量的添加,但需保证数据的隐私性.3)针对第三方收集者,可以考虑本地差分隐私技术对位置或其他敏感信息进行收集和发布,从数据源端遏制用户信息的泄露.
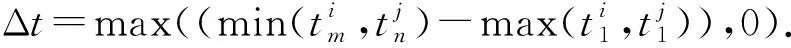
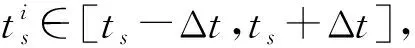
α×disto(Ti,Tj)+β×distv(Ti,Tj),1.2 差分隐私
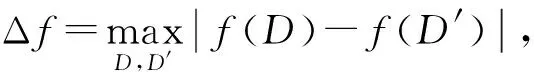

1.3 其他背景知识
1.4 攻击模型
2 满足差分隐私的轨迹数据发布方案
2.1 原始轨迹数据预处理
2.2 处理轨迹等价类


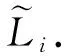
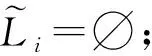


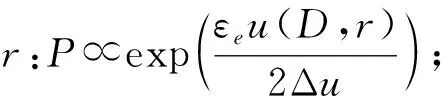
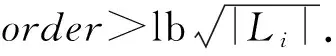

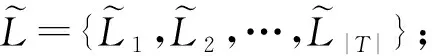

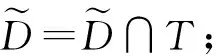

2.3 加噪前缀树的存储结构
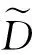
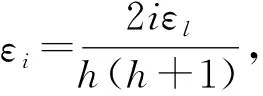

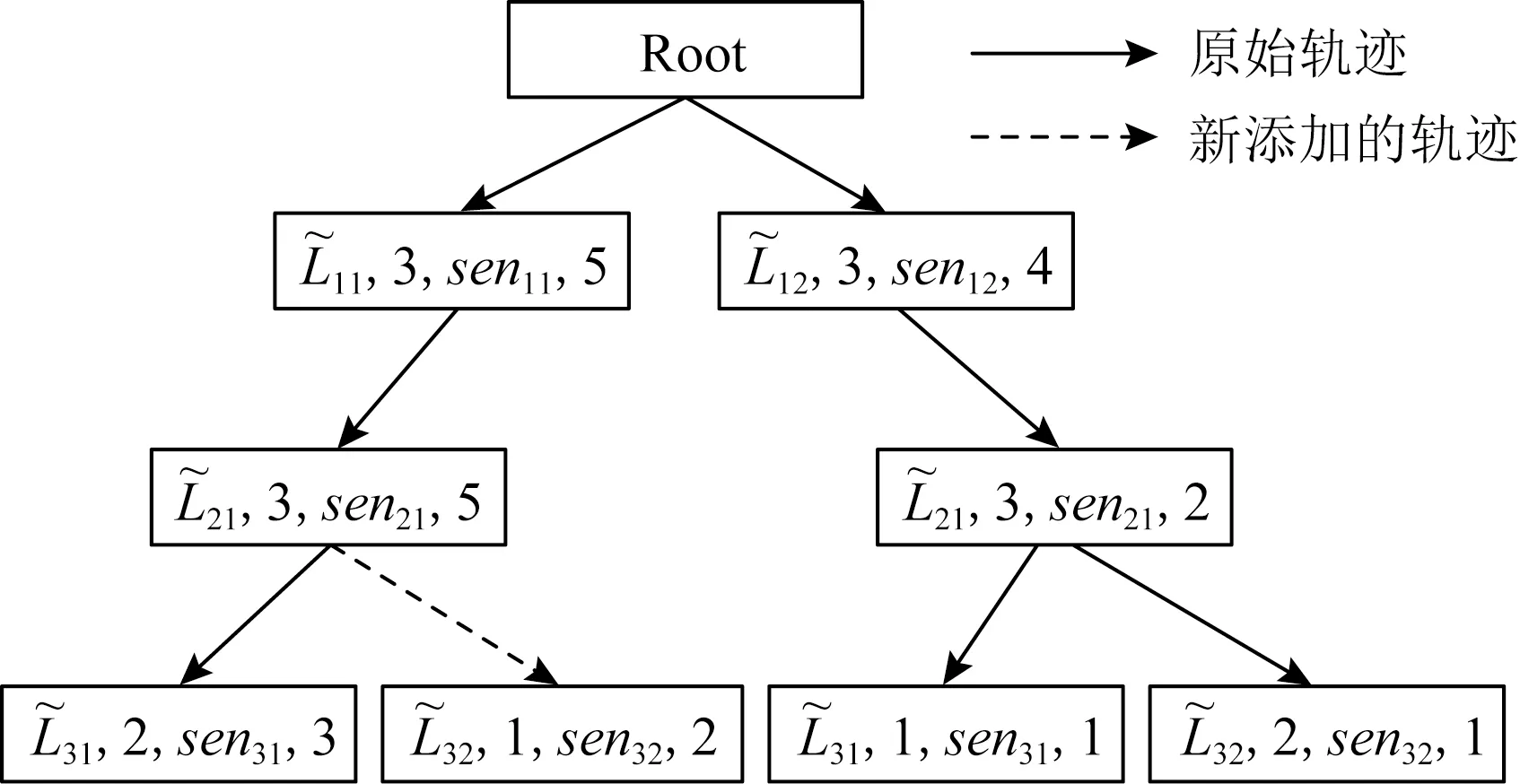
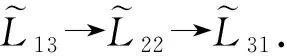

2.4 基于前缀树的差分隐私保护算法
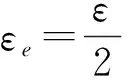
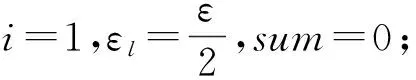
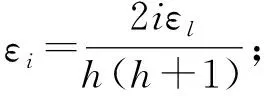

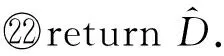

2.5 数据的查询过程

2.6 算法分析
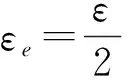

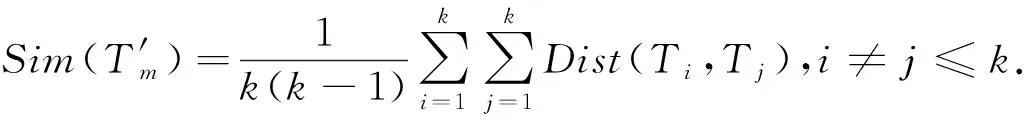
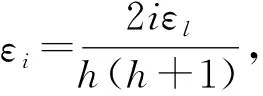
3 实验分析
3.1 数据可用性分析


3.2 隐私性分析
4 总结与展望
