基于变邻域模拟退火算法的多自动导引车任务分配优化
2021-11-05杨玮李然张堃
杨玮,李然,张堃
(陕西科技大学机电工程学院,西安 710021)
0 引言
近年来,电商行业发展迅速,电商订单规模不断扩大,且订单结构呈现多品种、小批量、多频次、短周期的特点,如何高效、准确、安全地对大规模货物进行储存以及根据订单快速完成拣选,这对涉及仓储物流企业的自动化设备提出了较高的要求[1]。自动导引车(Automated Guided Vehicle,AGV)作为实现仓储智能化、高效化的关键设备,是以移动机器人为核心的智能仓储系统的重要组成部分。在实际的应用过程中,单机器人系统在面对数量巨大、复杂程度较高的任务时,往往具有很大的局限性,而多机器人系统对任务的适用性、快速响应、可扩展性和经济性等方面都优于单机器人系统[2]。
多AGV 仓储系统提供了一种新式自动化订单履行方案,通过多个移动机器人、可移动货架、工作站以及复杂的控制系统,完成仓储系统中存储、拣选、打包以及运输等作业,相较于传统巷道式自动化立体仓库(Automatic Storage &Retrieval System,AS/RS),该系统同属“货到人”的作业方式[3],但其具有更加灵活的运行规则,可通过增减系统中AGV 的数量有效应对波峰波谷的订单变化,具有节省仓储空间、节约人工成本,从而提升单元坪效和人效等优势。
当多个AGV 执行一批订单任务时,在满足多种约束条件的情况下,为AGV 找到最优的任务分配方案,对最大限度提升仓储性能具有重要意义。现有研究中,在任务分配方面,王书亭等[4]针对任务分配难以满足多属性需求问题,提出了动态加权指派法,测验表明该方法具有更优越的综合评价性能;于琨等[5]针对嵌入式系统中任务分配问题,提出了一种多目标任务分配和调度算法,并证明了其结果比贪婪算法更好;胡华等[6]将Q-learning 引入到工作流任务分配问题中,提出一种针对多目标的强化贪婪迭代方法进行求解;陈友玲等[7]针对云制造环境下制造资源生产能力约束导致的任务分配不合理问题,建立了一种任务分配优化模型,采用改进多目标粒子群进化算法进行求解,并通过实例证明了该模型与算法的可行性和有效性;Farinelli 等[8]通过任务分配研究解决多机器人巡逻问题,提出贪婪算法和顺序单项贪婪算法,仿真结果表明所提出的在线调度方法能够提高系统性能;Luo等[9]提出了一种分布式任务分配算法,通过对任务进行分组以及计算每个机器人完成每个任务的收益,建立收益最大为目标函数的优化模型,从而求解得出最佳任务分配方案;Yacoub 等[10]采用预测控制的能量优化算法,在移动机器人行进过程中有效地控制速度并降低能耗,进一步解决了参数对能耗的影响问题;Guerrero 等[11]通过概率方法解决移动机器人任务分配问题,研究证明了通过模糊马尔可夫链可以在有限的步骤中快速收敛到平稳阶段,并且可以更好地预测系统未来的行为;Otte等[12]提出了拍卖算法解决多机器人任务分配问题,对六种拍卖算法进行了比较,评估了在不同的拍卖目标以及两种不同通信模型下系统拍卖绩效;赵文政等[13]提出面向多机器人协调运动规划的层级化任务分配方法,降低了任务分配计算量、减少共享空间内多机干涉可能性。
针对仓储系统中多机器人任务分配问题,蔡帛良等[14]以任务均衡为目标,建立多回路旅行商问题(Multi-Travelling Salesman Problem,Multi-TSP)的数学模型,利用快速非支配排序和精英策略的遗传算法(Genetic Algorithm,GA)解决任务分配问题;王振庭等[15]以转向次数、路程代价、最大任务等待时间为优化目标,提出了一种兼顾任务分配和路径规划的调度算法;范媛等[16]以任务自身代价和关联代价为目标,采取改进遗传算法、模拟退火(Simulated Annealing,SA)算法、随机分配算法三种方法并进行比较分析,证明其提出的遗传算法效果更优;徐源正[17]以多机器人到多任务点的总体代价最小为目标建立模型,提出一种改进遗传算法进行求解;张涛等[18]以时间和消耗为优化目标、以任务完成度为约束条件建立任务分配模型,提出了改进烟花算法,对比实验结果表明该算法在解集质量、解集覆盖度方面具有明显优势;Saeedvand 等[19]以机器人空闲时间、能源、总任务完成时间和均衡性为目标设计任务分配算法(Multi-Objective Multi-Humanoid Robots Task,MO-MHTA),在求解过程中首先采用约束K 型算法(Constraint K-Medoid,CKM)进行任务分区,其次采取非支配排序遗传算法对问题求解;陈明智等[20]构建栅格化仓库模型,以时间、协同度和路程为目标,提出了一种基于多层编码遗传算法多智能体任务分配算法;李腾等[21]以行走距离最短、机器成本最小及空闲率最小建立双层规划模型,设计遗传算法求解,进行实例仿真验证了模型的有效性;石楠路等[22]构建了考虑换电过程的AGV 作业调度混合整数优化模型,通过遗传算法进行求解。以上涉及多AGV 仓储系统的任务分配研究中大多仅以路径最短和任务均衡为目标,而未考虑总任务完成时间以及空负载情况下AGV 的耗电情况,同时多数学者仅研究了小规模情况下的任务分配问题,很少研究大规模任务下协同调度情况,然而现实中常常出现订单高峰期,较大规模订单同时出现往往需要调度更多机器人执行任务。在针对多AGV 仓储系统任务分配的智能算法设计方面,算法的求解精度和求解效率也有待进一步提高。
本文从综合考虑路径代价、时间代价以及任务均衡值代价的角度,以多AGV 仓储系统为研究对象,对其任务分配问题进行研究,并建立了考虑AGV 空载行驶和负载行驶的耗电情况的约束条件,设计变邻域模拟退火(Variable Nerighborhood_Simulated Annealing,VN_SA)算法对三种不同规模的任务分配问题进行优化求解。最后,通过仿真实验将变邻域模拟退火算法求得的任务分配结果与遗传算法求得结果比较,验证了变邻域模拟退火算法的有效性和优越性。
1 问题描述及模型建立
1.1 问题描述
多AGV 仓储系统采用分布式智能的思想,通过数以百计的移动机器人,将存放物品的货架抬取至仓储系统两侧工作人员所在的工作站前方,工作人员按照信号指示,从货架中拣选出相应订单货物或存放相应货物至货架,实现对于仓储系统中货物简约、高效的管理和访问。
某电商平台在某时段接收到一批订单,订单上的货物分布在m个不同可移动货架上等待多个AGV 抬取并搬运至工作站进行拣选,此时控制系统基于调度算法将任务分成n个子任务,调度n个空闲AGV 完成每个子任务,多AGV 仓储系统中包含t个工作站。作业流程具体描述为:
1)系统下达任务序列,多个AGV 将被分配到一个或多个订单任务。
2)AGV 经路径规划算法从充电站位置出发行驶至目标货架位置,将待拣选货架抬取送至工作站,由人工完成拣选工作,拣选完成后AGV将货架送回原位置。
3)AGV 从当前位置出发行驶下一个订单任务的目标货架位置,依次循环完成所有分配到的子任务。
由图1可以看出,多AGV仓储系统的作业具有较强的连续性,AGV 持续工作,因此对于AGV 的协作性有较高的要求,以便形成一个有机整体,而任务分配研究将直接影响多个AGV之间是否会发生冲突、系统任务分派是否合理,以及系统完成任务集合的整体效率等,是实现系统最优化的关键环节。

图1 系统中AGV搬运作业过程Fig.1 Process of AGV handling operation in system
1.2 多AGV仓储系统任务分配模型建立
1.2.1 条件假设及参数定义
为了方便建模与分析,提出如下假设:
1)系统中单个AGV均能独立完成任务且能力相同。
2)AGV在相同行驶状态下行驶速度相同。
3)仅考虑AGV在完成任务过程中所花费的代价。
4)每个AGV 花费的各个代价的总和为完成任务花费的总代价。
模型参数及变量定义为:AGV 数量集合由R={r1,r2,…,rm}表示;可移动货架集合由S={s1,s2,…,sk}表示;工作站集合由W={w1,w2,…,wn}表示;m为AGV 个数;k为可移动货架个数;n为工作站个数;p为一批订单中任务的个数;SC为路径代价;TC为时间代价;BC为任务均衡值代价;dij为AGV 从i点货架行驶至j点货架最短距离,其中i=1,2,…,k,j=1,2,…,k;ujw为AGV 抬取第j点货架到对应第w点工作站之间的最短距离,其中j=1,2,…,k,w=k+1,k+2,…,k+n;c1为AGV 在负载行驶下单位距离的成本;c2为AGV 在空载行驶下单位距离的成本;T为一批任务中订单的数量;v1为AGV 在负载行驶下的速度;v2为AGV在空载行驶下的速度;AGVrl为被指派任务的第l个AGV;xlt为是否指派AGVrl完成第t个任务;clj为AGVrl完成订单任务sj所花费的路径代价;tlj为AGVrl完成一个订单sj任务所花费的时间代价;r为工作人员拣选时间;tr为AGV 抬取货架时间;tf为AGV 释放货架时间;p(r)为第r台AGV 的剩余电量;v为安全电量百分比。
1.2.2 目标函数建立
为提高仓储系统拣选作业效率,多台AGV 任务分配问题需要综合考虑路径代价最小、时间代价最小、任务均衡值代价最小:

其中:X表示一种任务分配方案;SC表示路径代价;TC表示时间代价;BC表示任务均衡值代价,可以根据实际需求确定3种代价的权重ω。
1)路径代价。当AGV 接收到订单任务后,将从起始点出发行驶至待拣选货架,将货架抬取后送至拣选台,待工作人员拣选完成后将货架送回原位,此过程为AGV 完成一个订单任务花费的路径代价。采取完成总订单任务中每个AGV 所花费的路径成本之和作为总路径代价。

其中:xlt是0-1变量,若指派AGVrl完成第t个任务,则xlt=1;否则xlt=0。完成订单任务sj所花费的路径代价:

其中:关联代价c2dij是指AGV 执行上一个任务结束到下一个任务开始所花费的代价,即AGV 从当前任务结束货架位置行驶至新的任务开始货架位置所花费的成本;自身代价2c1ujw是指AGV 单独完成某个任务所花费的代价,即包括从待拣选货架位置行驶至对应工作站加上由工作站返回原目标货架位置所花费的成本。
2)时间代价。将AGV执行订单任务时的行驶速度简化为空载匀速行驶速度及负载匀速行驶速度,不考虑行驶过程中外力导致的加减速问题,将AGV抬取货架及释放货架的时间、工作人员拣选时间均设定为固定值;那么AGV完成一个订单sj任务所花费的时间代价tlj为其空载行驶时间、负载行驶时间、两次抬取货架、两次释放货架及工作人员拣选时间之和,即:
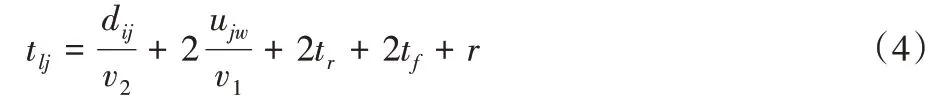
多台AGV 完成一批订单任务的总时间代价取AGV 中完成任务时间代价最大的表示,即:

3)任务均衡值代价。系统中每个AGV 执行任务序列所花费的路径代价应尽可能地相近,以保证系统中AGV 的有效利用率较高,故采取AGV路径代价的方差,反映其离散程度。
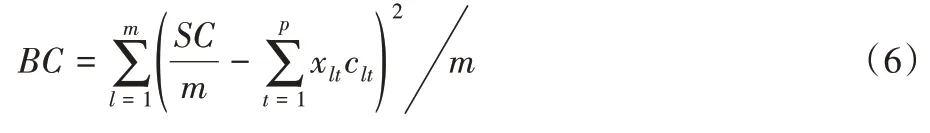
1.2.3 约束条件建立
根据多AGV 仓储系统实际作业流程,设定如下约束条件。
1)电量约束。机器人在执行任务序列的过程中,分为负载和空载两种状态[23],而机器人在空负载状态下耗电量也不同,随着AGV 电池电量的消耗,剩余行驶距离呈加速减少状态,直至电池电量完全消耗剩余行驶距离为0[24]。
根据电池电量消耗情况与剩余里程关系图(图2)建立函数等式:

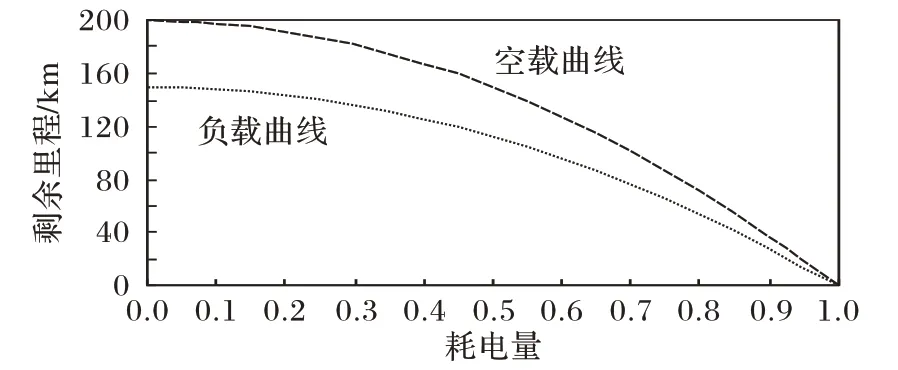
图2 AGV耗电曲线Fig.2 AGV power consumption curve
继而考虑每个AGV 行驶里程均在安全电量范围,即预留安全返回充电站的电量[25]。由于在剩余相同电量时,空载状态可行驶剩余里程数大于负载状态可行驶剩余里程数,从而保证负载AGV 能安全返回充电站的电量也可能保证空载AGV安全行驶,故只考虑负载形式下电量约束情况。

每台AGV 均在安全电量约束范围内行走,且有安全返回充电区电量:

2)一个订单任务只允许一个AGV完成。

3)一批订单任务全部指派给多个AGV。

4)变量取值约束。

2 变邻域模拟退火算法设计
2.1 算法描述
多AGV 仓储系统任务分配问题是NP-hard 问题,本文设计了变邻域模拟退火算法进行求解。模拟退火(SA)算法是模拟自然界退火现象得到,利用物理学中固体物质的退火过程与优化问题的相似性,从某一初始温度开始,随着温度的不断下降,结合概率突变特性在求得的解空间随机寻找全局最优解的算法。SA 要求较高的初始温度、较低的终止温度、较慢的降温速率,以及各个温度下多次抽样,因此优化过程较长。变邻域搜索(Variable Neighborhood Search,VNS)算法是一种改进的局部搜索算法,通过不同的动作构成的邻域结构完成交替搜索,获得局部最优解。
本文采用变邻域模拟退火(VN_SA)算法进行模型求解。首先,利用模拟退火算法构造初始解并修正;其次,进行变邻域操作,在搜索过程中系统地进行邻域转换,拓展其搜索范围得到局部最优解;最后,通过三种邻域扰动操作进行全局搜索,并以概率突变特性使解跳出局部最优,找到全局最优解。变邻域模拟退火算法流程如图3所示。
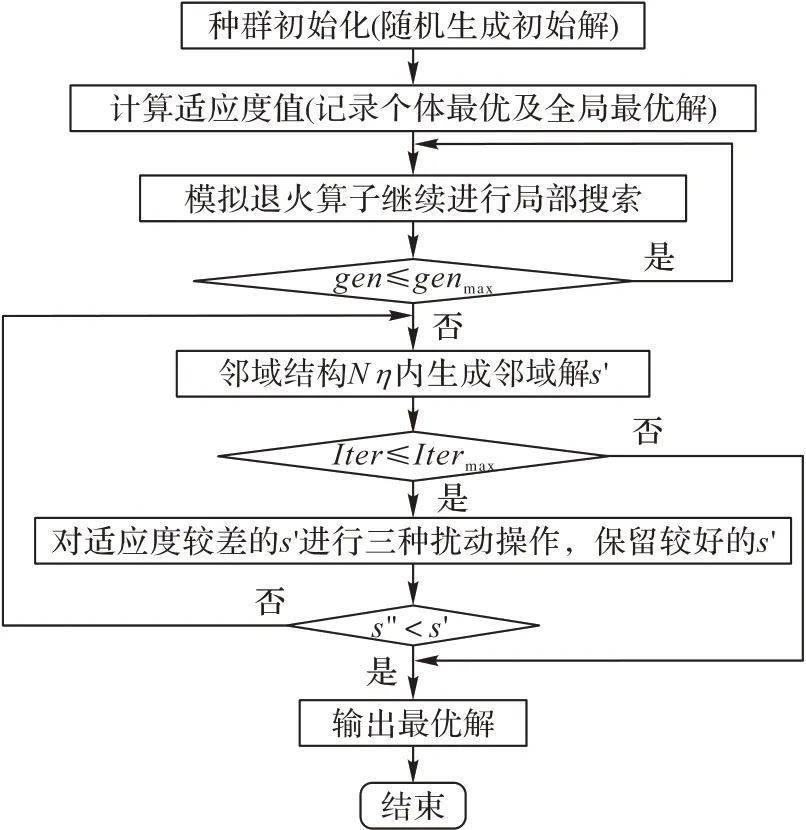
图3 变邻域模拟退火算法流程Fig.3 Flowchart of VN_SA algorithm
2.2 编码设计
基于多AGV 仓储系统任务分配模型特点,采用双个体整数编码方式,即编码序号分别代表订单任务的编号和AGV 的编号。若有M个任务、P个AGV,由于M≠P,考虑任务均衡代价设置P以P(P)=M/P的概率出现以将任务编号补齐。每条编码分别代表任务及AGV 的顺序,状态向量Mi和Pi分别构成1个订单任务及1 台AGV,其对应关系为1 个可行的任务方案,即第M个任务由第P个AGV 完成。例如,订单任务及AGV的状态分别为Mi={m1,m2,…,mn}={3,5,…,8},Pi={p1,p2,…,pn}={2,1,…,2},此时对应的解码为[(3,5,…,8)(2,1,…,2)],即系统以[3,2],[5,1],…,[8,2]的组合方式完成任务分配。
2.3 适应度函数
本文的优化目标是完成所有订单任务所花费的总代价最小,则适应度函数为:
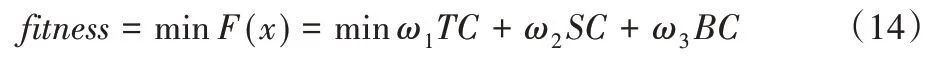
2.4 算法步骤
多AGV仓储系统任务分配模型的VN_SA具体步骤如下:
步骤1 基于多AGV 仓储系统任务分配模型特点,初始化种群和参数,包括Markov 链长度、初始温度T、最大退火次数genmax和温度下降比例rdown,确定邻域结构集合Nη={N1,N2,…,Nη}及每个邻域结构的迭代次数Itermax,根据约束条件(9)~(11)生成初始任务分配结果。
步骤2 计算适应度函数值,记录个体最优值及全局最优解sbest=s0。适应度函数为完成所有订单任务所花费的总代价。
步骤3 模拟退火算子将s0作为初始解,继续进行局部搜索,以Tt=T0(1+t)作为降温函数进行退火降温,判断内循环迭代次数是否达到最大:若达到最大则转入步骤4;否则重复进行退火操作,直至达到平衡态。
步骤4 在解s的邻域以P=0.5 的概率更新AGV 的位置,并生成邻域解s',判断算法是否达到最大迭代次数Itermax:若达到则输出适应度函数值最小的解,即问题的最优解;否则转步骤5。
步骤5 对邻域解的适应度值进行判断,若s'>s0,则对邻域结构进行扰动操作,改善当前解的质量,进行全局开发,得到新解s″,扰动分为3类:
1)“插入”操作。插入是指是指将某段连续的任务节点进行单链路段变换,随机产生个任务节点,将此路段插入某个位置之后,生成新的路径,如图4(a)所示。
2)“交换”操作。交换是指在单链内部选择两条任务路段进行部分位置互换,生成一条全新的路径,如图4(b)所示。
3)“2-opt”操作。2-opt 是指在单链内部选择一段任务路段,将该路段翻转后得到新的路径,若翻转后的总代价小于翻转前,则进行路径覆盖保留;否则,取消翻转,如图4(c)所示。
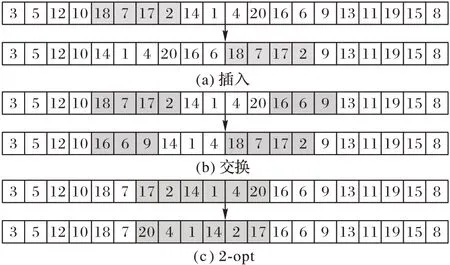
图4 三种邻域扰动操作演示Fig.4 Demonstration of three neighborhood perturbation operations
若s' 步骤6 更新种群,计算所有新个体的适应度值,并与初始解集合的适应度值进行对比。 步骤7 判断迭代次数是否达到最大,若达到则输出最优解,即得到总代价最小的任务分配结果;否则返回步骤2。 将整个多AGV 仓储系统抽象成一个栅格化地图(图5),以仓储系统左下角为原点建立直角坐标系,仓库布局为纵向10 个单元货架区,横向6 个单元货架区,每个单元货架为2 排8 列,共有960 个可移动货架,10 个服务于拣选作业及补货作业的工作站均匀分布于仓储系统两侧,横向巷道和纵向巷道宽度均为1.5 m,每个可移动货架长度和宽度均为1 m;其次,根据参数明确系统中各个设备的坐标,其包括可移动货架、AGV和工作站。 图5 仓库布局Fig.5 Warehouse layout 仓库布局参数变量为:ws为可移动货架宽度;ls为可移动货架长度;nca为横向过道数量;wca为横向过道宽度;wsca为侧面横向过道宽度;wa为巷道宽度;nsw为侧面工作站数量;W为系统长度;nw为系统工作站总数量;L为系统宽度。得到系统的长度、宽度分别为: 针对单元可移动货架模块,该模块坐标表示为:(xe,ye),xe=1,2,…,nca+1,ye=1,2,…,na+1,可移动货架在一个模块中的坐标表示为(xes,yes),xes=1,2,…,x,yes=1,2,…,y。所有可移动货架集合表示为: 规定(xsl,ysl)为目标货架坐标,则: 其中:P(xsl,ysl)为集合S中指定一个元素的概率,因为采取随机分布,故P(xsl,ysl)=12x(na+1)(nca+1)。 规定(xd,yd)为AGV 待命点坐标,因为采取成点驻留策略(Point-Of-Service-Completion,POSC),故可以通过公式计算。 规定(xwi,ywi)为工作站位置坐标,系统左右两侧均匀布置工作站,左侧工作站服务于拣货作业,右侧工作站服务于补货作业,得出工作站坐标如下: 计算最短路径dij、ujw过程如下: 1)AGV从待命位置行驶至目标货架的最短距离dij。该段行驶状态为空载状态,可以通过货架底部空间行进,因此该段移动行驶距离为待命位置和目标货架之间的曼哈顿距离: 2)AGV从目标货架行驶至工作站的最短距离ujw。该段行驶状态是负载状态,因此AGV只能沿巷道和横向过道行走,目标货架(xsl,ysl)到工作站i的行走距离可以分为以下4种情况: ye为偶数、yes为奇数或ye为奇数、yes为奇数:AGV首先行驶至相邻巷道(行驶距离为(ls+wa)/2),然后行驶至侧面横向过道(行驶距离为xsl),最后行驶至工作站i(行驶距离为|ywi-ysl+(ls+wa)/2|)。 ye为奇数、yes为偶数或ye为偶数、yes为偶数:AGV首先行驶至相邻巷道(行驶距离为(ls+wa)/2),然后行驶至侧面横向过道(行驶距离为xsl),最后行驶至工作站i(行驶距离为|ywi-ysl-(ls+wa)/2|)。 3)AGV从工作站返回原存储位置的最短距离ujw。该段行驶状态是负载状态,AGV只能沿巷道和横向过道行走,行走距离可以分为以下4种情况,其中(xf,yf)为返回巷道初始点坐标: ye为偶数、yes为奇数或ye为奇数、yes为奇数,AGV首先从工作站行驶至上方返回巷道初始点(行驶距离|yf-ywi|),紧接着从返回巷道初始点行驶至存储位置对应的横向巷道初始点(行驶距离|xsl-xf|+(x-xes)×ws+(ws+wca)/2),接着从横向巷道初始点行驶至存储位所在巷道与横向巷道交叉点(行驶距离|ysl-yf|+(ws+wca)/2),然后行驶至存储点所在巷道位置(行驶距离为(x-xes)×ws+(ws+wca)/2),最后返回存储位置(行驶距离为(ls+wa)/2)。 ye为奇数、yes为偶数或ye为偶数、yes为偶数:AGV首先从工作站行驶至上方返回巷道初始点(行驶距离|yf-ywi|),紧接着从返回巷道初始点行驶至存储位置对应的横向巷道初始点(行驶距离|xsl-xf|+(x-xes)×ws+(ws+wca)/2),接着从横向巷道初始点行驶至存储位所在巷道与横向巷道交叉点(行驶距离|ysl-yf|-(ls+wa)/2),然后行驶至存储点所在巷道位置(行驶距离为(x-xes)×ws+(ws+wca)/2),最后返回存储位置(行驶距离为(ls+wa)/2)。 为验证多AGV 仓储系统适应不同规模任务量的任务分配问题,设计具有不同参数场景的问题进行数值实验仿真。多组参数实验得到的最优参数设置如表1所示。 表1 数值实验参数设置Tab.1 Numerical experimental parameter setting 以系统分别执行任务量为20、50、100 拣选作业为例进行3 组仿真实验并分析。依据不同任务规模,仓储系统布局以及AGV 数量均随着任务量的增加而增加,3 种规模的系统参数如表2所示。 表2 不同规模任务量系统参数Tab.2 System parameters of different scale tasks AGV 的安全电量是总电量的10%,即可满足AGV 从仓储中任意位置返回充电区。其中20 条目任务量时每个AGV 剩余电量百分比如表3所示,任务列表如表4所示。 表3 AGV剩余电量Tab.3 AGV remaining power 表4 随机生成任务列表(20条目)Tab.4 Randomly generated task list(20 entries) 根据程序随机所得一组任务序列为:1 号AGV[S→14→S],2号AGV[S→1→4→18→12→2→S],3号AGV[S→10→11→5→9→S],4 号AGV[S→6→8→3→7→20→17→S],5 号AGV[S→16→13→19→15→S]。总目标值为1 097.053 5。 经过VN_SA 优化后所得一组任务序列为:1 号AGV[S→16→13→5→S],2 号AGV[S→18→9→3→8→S],3 号AGV[S→12→6→20→S],4 号AGV[S→14→15→7→4→11→S],5 号AGV[S→1→2→10→17→19→S]。总目标值为910.115 7,优化效率为20.5%。 为验证算法有效性,将GA与VN_SA在不同任务规模下运行30次的求解模型结果平均值进行对比,结果如表5所示。 表5 不同算法在不同任务规模下的实验结果Tab.5 Experimental results of different algorithms under different task scales 由表5可以看出,VN_SA在三种不同任务规模下求解的路径代价值、时间代价值以及任务均衡值均小于GA的计算值。 表6 为VN_SA 和GA 分别相较于随机算法(Randomized Algorithm,RA)计算得到的优化效率。由表6 可以看出,VN_SA 计算的任务分配均衡值优化效果更好,即AGV 任务分配更加均衡和合理,随着作业规模的不断增大,VN_SA相对于GA的优化效率和平均计算时间的优势不断扩大,表明该算法给更加适用于大规模任务分配问题。 表6 不同算法在不同任务规模下的优化结果Tab.6 Optimization results of different algorithms under different task scales 图6 所示为GA 和VN_SA 两种算法对任务分配问题在不同任务规模下的算法收敛效果。 图6 不同任务量下算法收敛效果Fig.6 Convergence effect of different task load algorithms 由图6 的收敛曲线和适应度值可以看出,GA 收敛速度快,但容易陷入局部最优;而本文提出的VN_SA 在退火过程下迭代初期求解效果表现较好,通过邻域搜索扩大搜索范围,扰动操作结合概率突变使算法跳出局部最优,具有更高的算法精度,并且随着问题规模的增大,优化效果愈加明显。 本文针对多AGV 仓储系统任务分配问题进行了详细的调度分析,通过分析多AGV 仓储系统管理特点以及作业流程,考虑AGV 执行任务耗电量需求,建立了以总代价最小为目标函数的优化模型。针对该模型,本文采用VN_SA 进行优化求解,对初始解进行模拟退火内循环的同时系统地改变邻域结构集合,融入扰动操作从而增强算法的全局性,提高了算法的性能。最后,将VN_SA 与GA 所得结果进行比较,结果表明,VN_SA 求得的总目标函数、路径代价、时间代价和任务均衡值的最优解均优于GA,且其在求解任务量规模较大的任务分配问题上优势更加突出,能够实现多AGV 仓储系统任务分配的协调优化和系统效率的提高。 本文主要针对多AGV 仓储系统中固定货架位置的多AGV 任务分配问题进行了优化研究,即当拣选完成后货架返回原存储位置,但是,在仓储运作过程中可能会根据货物的出入库频率调换货架位置,在这种情况下拣选完成的货架不一定返回原存储位置,今后将考虑货架位置调换情况下AGV 的任务分配与调度的情况,以最大限度提高仓储效率。3 实例与结果分析
3.1 仓库模型
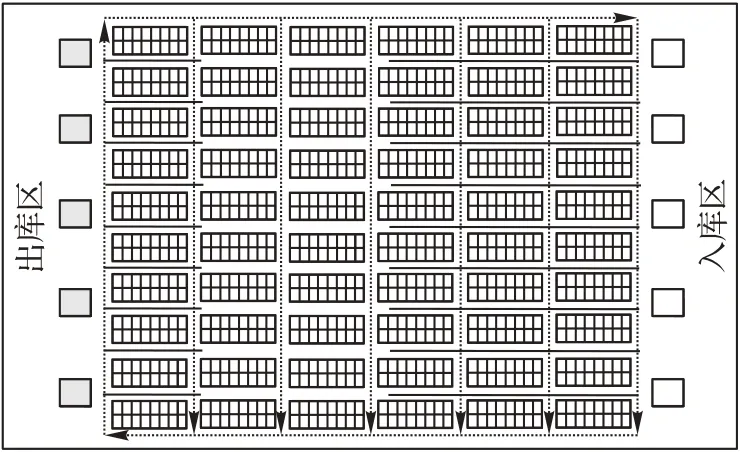
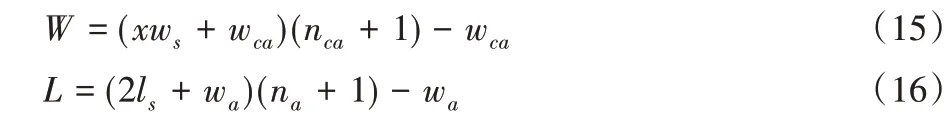
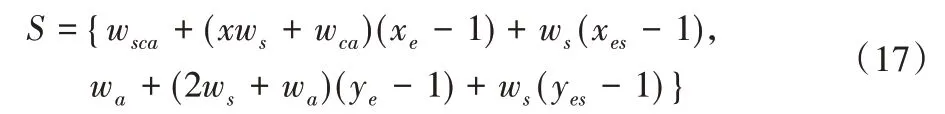
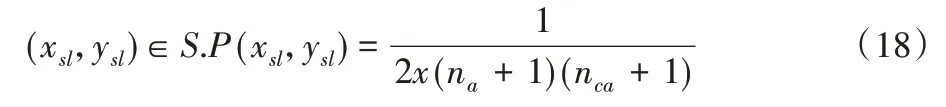


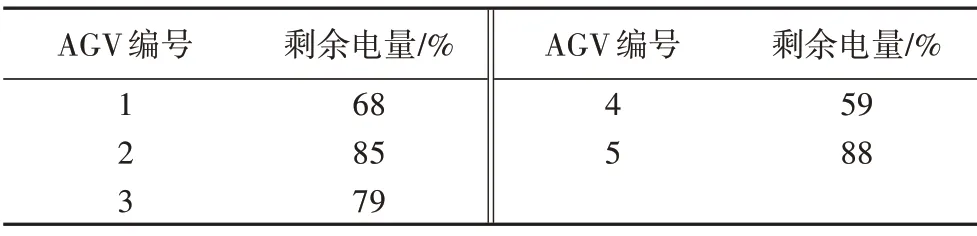
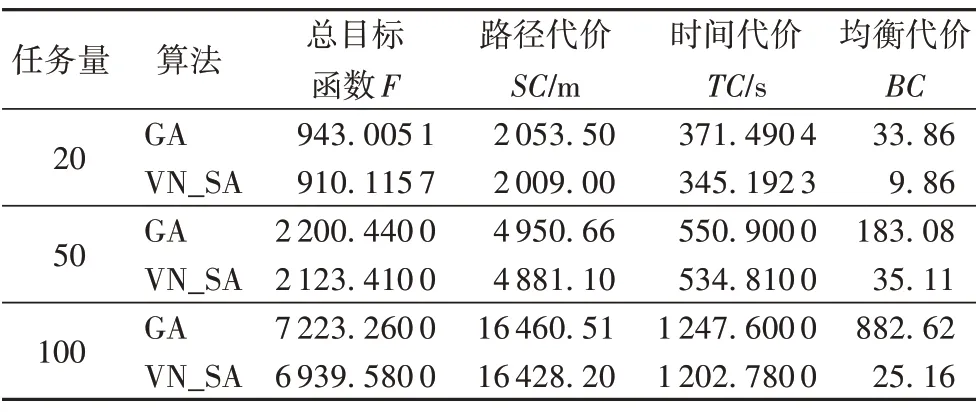
3.2 结果分析




4 结语
