改进鲸鱼优化支持向量机的交通流量模糊粒化预测
2021-11-05童林,官铮
童 林,官 铮
(1.六盘水师范学院物理与电气工程学院,贵州六盘水 553004;2.云南大学信息学院,昆明 650500)
0 引言
准确把握交通流量发生趋势和变化区间是合理调控交通负荷的重要依据,但由于交通流量与其影响因素之间存在着复杂非线性关系,难以建立精确的模型。众多的研究中,参数模型中的时间序列方法用于交通流量预测取得了良好的预测效果[1],但对交通流量的波动性缺乏考虑且不适用于大数据样本。为了更好地捕获交通流量中的非线性时空关系,机器学习方法等非参数模型被广泛应用在交通流量预测中:文献[2]中使用基于高斯过程的机器学习模型对交通流量预测,评估可知机器学习方法优于时间序列模型;文献[3]中提出了一种基于支持向量机(Support Vector Machine,SVM)的短时交通流量预测模型,并验证了SVM 模型在精度、收敛时间等指标上均优于BP(Back Propagation)神经网络,但在核参数g和惩罚系数c参数选择上存在难点,而这两个参数的选取对SVM模型预测结果影响较大;文献[4]提出了基于支持向量回归机的交通状态短时预测方法,但同时也提到了该模型的参数优化、预测精度的提高等还需要进一步的研究。
随着智能算法的提出,众多智能优化方法被用于优化机器学习模型及神经网络算法的参数,如:文献[5]提出了遗传算法(Genetic Algorithm,GA)优化BP 神经网络的短时交通流混沌预测,有效降低了BP神经网络预测模型陷入局部极小值的概率;文献[6]提出了采用粒子群优化(Particle Swarm Optimization,PSO)算法对多核SVM 的参数进行优化,增强了模型的非线性拟合能力;文献[7]提出了基于无负约束理论(No Negative Constraint Theory,NNCT)的权重积分方法来汇总多个长短期记忆(Long Short-Term Memory,LSTM)网络的预测结果,并使用人口极值优化(Population Extremal Optimization,PEO)对权重系数进行了优化。此类智能算法存在着搜索精度低、易早熟收敛、后代迭代效率不高等共性问题,易在寻找机器学习模型最优参数时陷入局部极值进而降低预测精度。
部分研究者提出了基于组合模型的交通预测模型,如:文献[8]提出了基于K-means 和极限学习机(Extreme Learning Machine,ELM)组合模型的短时交通流量预测算法,与单一机器学习模型相比,其预测精度有较大提高,但其缺陷是由于网络结构复杂,隐含层的节点数需要在训练前由用户设定或通过多次实验获得最优节点数,导致算法时间复杂度较高;文献[9]提出了基于K最近邻(K-Nearest Neighbor,KNN)回归的短时预测模算法,该算法的参数同样需要人工设定,缺乏研究如何学习算法中的模型参数达到模型自动优化;文献[10]使用了自组织映射神经网络(Self-Organizing feature Map,SOM)和概率神经网络(Probabilistic Neural Network,PNN)进行交通流模式划分和对交通流模式进行匹配,但没有解决交通流波动较大时预测精度较低的问题。上述组合非参数模型通常需要更多时间和计算量来学习最佳参数,限制了算法的实际应用。随着计算机计算资源的大幅度提升,深度学习在交通流量预测领域得到了应用,如:文献[11]提出了基于时空节点选择和深度学习的城市道路短时交通流预测;文献[12]提出了基于深度学习的短时交通流量预测,但深度学习为追求神经网络精度,造成模型过深以及计算代价高昂,在硬件资源匮乏时难以满足低时延交通流量预测的要求。
交通流量预测的目的是服务于交通调度规划与后续的协调控制,根据以上现有研究工作可知使用机器学习方法较多是预测交通流量的定量值,由于交通流量预测过程中存在较多的不确定因素,且交通流量变换具有一定的周期性和区间特征(即某个周期时段往往在某个区间内波动),如果仅以短时定量值预测作为控制依据,会缺乏全局性,造成调度与控制策略的频繁切换,不利于实际交通环境应用,对交通流量变化趋势和变化区间的预测更有利于后续的交通规划和流量控制。本文在充分考虑其他研究的基础上,提出了采用模糊信息粒化(Fuzzy Information Granulation,FIG)和改进的鲸鱼优化算法(Improved Whale Optimization Algorithm,IWOA)的SVM交通区间预测方法。
所提方法主要工作有:1)采用鲸鱼优化算法(Whale Optimization Algorithm,WOA)对SVM 的参数进行优化提高了SVM 预测的准确度;同时对WOA 进行改进,进一步提高了SVM 参数优化的准确性,避免算法搜寻SVM 最优参数时陷入局部最优。2)在交通流量定量值预测的基础上引入模糊信息粒化的思想,解决了单一的交通流量预测模型不能表征预测结果的问题,同时给出交通流量预测值和其变化区间,为交通流量预测提供一种更可靠的方法。3)FIG 方法使得交通流量可以从传统点预测转向区间预测,另外,还可通过缩短和扩增FIG 时间窗的宽度,对交通流量进行中短期或中长期预测,并可以模拟交通流的波动区间。实验结果表明,本文所提的基于FIG 和IWOA-SVM 的交通流量区间预测模型,不仅提高了交通流量预测的准确性,而且能够解决单一的交通流量预测模型存在的预测结果可靠性低的问题,为智能交通流量监测提供更有效的信息。
1 交通流量变化区间预测原理
1.1 交通流量区间预测方法
本文从交通流量变化区间预测出发,提出如图1 所示的交通流量区间预测建模策略,模型主要按照以下3 个方面进行构建:
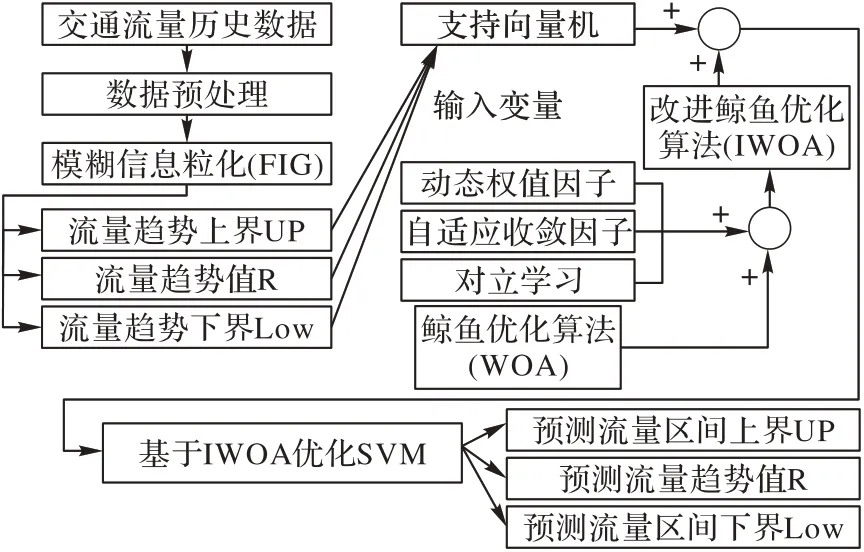
图1 交通流量区间预测建模策略Fig.1 Traffic flow interval prediction modeling strategy
1)针对WOA存在搜索精度低、易陷入局部最优的缺点,提出了IWOA。首先将动态对立学习引入到WOA的种群初始化中,改善算法初始种群质量;并通过非线性函数代替了WOA参数的线性选择,计算数据的变化趋势并动态更新模型的超参数,提高了WOA在高维数据中的收敛速度和预测精度。
2)考虑到SVM 模型在惩罚参数和核函数的选择上存在难点和IWOA 在求解高维数据优化问题上的优势,提出了一种IWOA 对SVM 进行优化的IWOA-SVM 交通流量定量值预测模型。
3)影响交通流量变化因素较多,导致交通流量预测波动频繁,仅靠定量值进行预测难以准确地表征其真实交通状况,带来交通调控方向错误。针对交通流量定量值预测不能表征预测结果可信度的问题,本文模型结合IWOA-SVM 算法和模糊信息粒化思想,提出了一种基于IWOA-SVM 和FIG 的交通流量变化区间预测方法,实现交通流量预测值和预测区间的同时预测。
与传统SVM 算法对定量值预测的思路不同,本文提出的实现过程交通流量定量值经过模糊信息粒化后能够根据窗口数分解为三个部分上界(Up)、趋势值(R)和下界(Low),在SVM 中采取相同的惩罚函数c和核参数g不能够很好地学习三种流量的变化规律,因此利用改进的鲸鱼算法寻找SVM 的最佳超参数,分别为cUp和gUp、cR和gR、cLow和gLow,其流程如图2 所示。得到SVMUp、SVMR和SVMLow这三种SVM 模型对交通流量变化区间分别进行预测。最后建立了FIG-IWOA-SVM 模型,以进一步增强预测交通流量区间的能力,使FIG-IWOASVM模型拥有更高的交通流量区间预测精度。
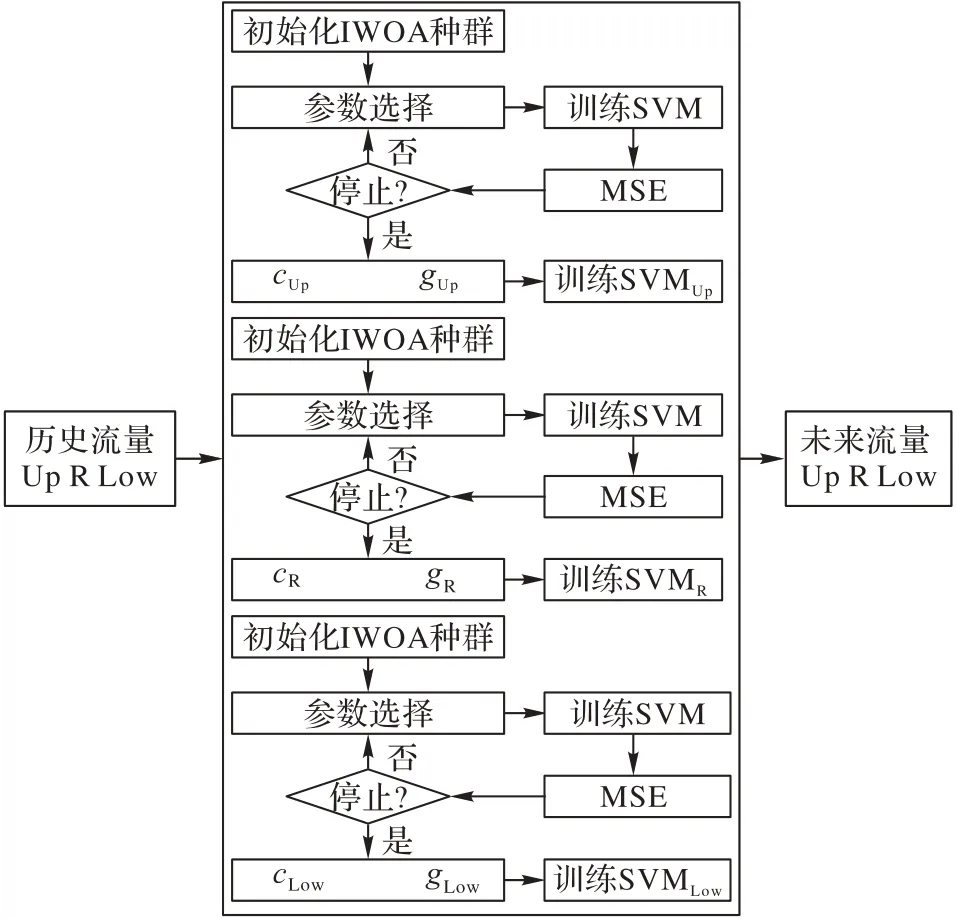
图2 IWOA优化SVM超参数流程Fig.2 Flowchart of IWOA optimizing SVM hyperparameters
1.2 模糊信息粒化
信息粒度(Information Granulation,IG)计算被应用于模拟人类思维并解决复杂问题。它通过相似性、函数逼近和区分将整体分为几个部分,每个部分都是一个信息粒。通过信息粒化研究信息的形成、表示、粗细、语义解释等。在信息粒化的基础上,Zadeh[13]于1979年首次提出FIG,如式(1)所示:

其中:x是实数集合R中的变量;G作为R的模糊子集,由隶属函数μG来刻画;λ表示x属于G的可能性概率。首先,通过划分每个子间隔作为窗口并选择窗口大小,可以维护数据信息,简化数据序列,并使其易于研究。然后,对一个窗口进行模糊处理以生成许多模糊颗粒以替换相关信息。
假设交通时间数据序列为X=(x1,x2,…,xn),并划分6 个数据序列为一个窗口,可得交通时间序列数据的信息粒化过程如图3所示。
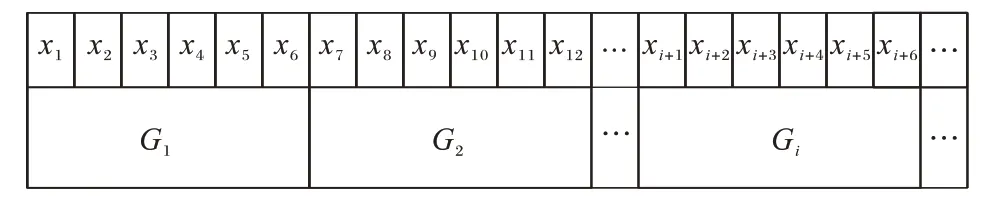
图3 交通时间序列数据的模糊信息粒化窗口划分Fig.3 Fuzzy information granulation window partitioning of traffic time series data
对数据进行模糊粒化时需要确定具体的隶属函数,模糊颗粒的常见模糊隶属度函数由三角形、高斯等组成。三角形模糊隶属度函数[14]如式(2)所示:
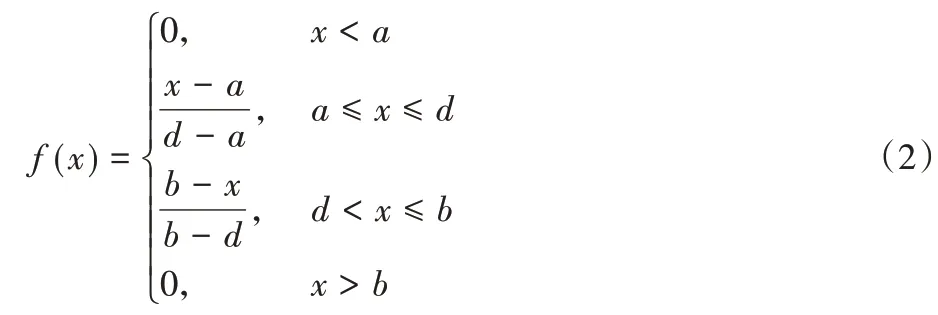
式中:x为模糊论域中的变量;a和b分别为模糊上界和模糊下界;d为模糊核参数。三角形模糊隶属函数如图4所示。
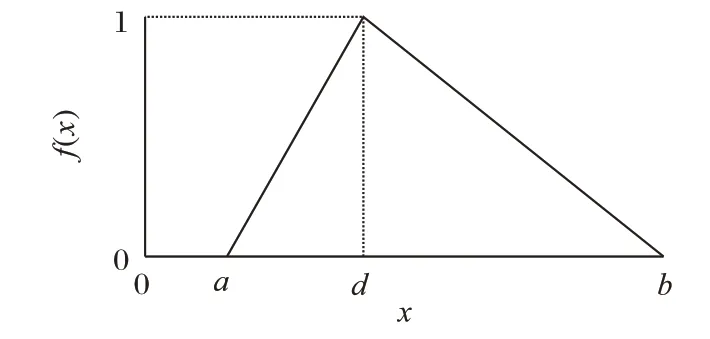
图4 三角形模糊隶属函数Fig.4 Triangle fuzzy membership function
1.3 鲸鱼优化算法
WOA 是Mirjalili 等[15]于2016 年提出的一种新颖的自然启发式优化算法。根据鲸鱼捕食的方式提出了鲸鱼狩猎行为的数学模型,包括3个部分:随机搜索、包围捕食、攻击猎物。
1)包围猎物。
座头鲸可以发现诱饵并将其包围,在确定最佳搜索者代理后,其他搜索者将根据最佳搜索者更新其职位。此行为[15]由式(3)表示:

式中:r1和r2为[0,1]的随机向量;e为收敛因子,收敛边界为2到0,定义为:

式中tmax为最大迭代次数。
2)Bubble-net攻击。
鲸鱼利用螺旋运动和向上运动来制造气泡,并使用泡泡狩猎策略捕食猎物。有两种方法可以模拟座头鲸的泡泡网攻击行为:一种是收缩包围机制;另一种是位置的螺旋更新。通过缩小包围或螺旋运动,鲸鱼更接近诱饵。在螺旋更新位置方法中,其数学模型[15]如式(7)所示:

式中:D=为鲸鱼与当前全局最优个体之间的距离;k为对数螺旋形状的常数;l为[−1,1]的随机数。
座头鲸在围捕猎物时不仅以螺旋形态游向猎物,还要收缩包围圈,要对此行为建模,假设鲸鱼在围捕猎物更新动作时选择收缩包围机制和螺旋更新位置概率为50%,数学模型[15]如式(8)所示:
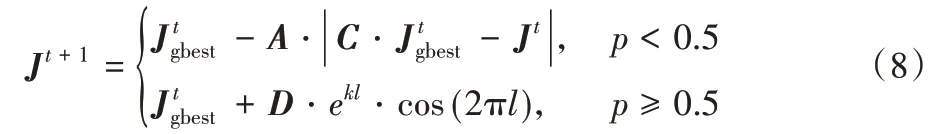
式中p为[0,1]的随机数。
3)随机搜索。
搜索猎物的过程中,为保证WOA 的全局探索能力,即在更大的搜索范围内找到更好的候选解,通过对系数向量|A|值的判断选择鲸鱼搜索方式。当|A|>1 时,鲸鱼在收缩包围圈外游动,鲸鱼会根据周边鲸鱼的位置进行随机搜索,鲸鱼随机搜索数学模型[15]式(9)所示:
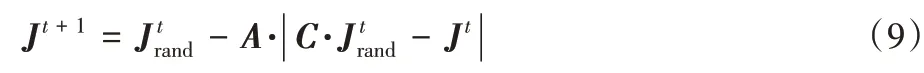
2 改进的鲸鱼优化算法
2.1 鲸鱼优化算法的改进
1)对立学习。
WOA 在首次迭代之前,需要选取一组随机的值用来初始化种群个体。由于可行解范围较大,存在初始化位置选择盲目的问题,容易造成初始搜索位置不佳,因此,改善初始种群的位置可以加快算法收敛。基于对立学习(Opposition-Based Learning,OBL)[16]已被广泛应用于各种算法初始的学习阶段,以增强算法的搜索能力[16],其核心思想是通过计算当前值及其对应的对立值来寻求更好的候选解决方案,从而丰富开发空间。对立学习定义如式(10)所示:

将对立学习拓展到高维,形成多维对立学习[16]如式(11):

式中:ub和lb为高维可行解的上下界,ub和lb为高维可行解的上下界向量,然后选择适应度较好的种群用来对算法进行初始化。为了进一步增强OBL 策略,本文将对立学习做出一定的改进,在对立学习的基础上添加随机因子改进为动态对立学习,该算法具有搜索空间不对称和动态调整以及随机产生相反数的特征。动态对立学习定义如下:

式中:JO为经过动态对立学习的种群位置;r3为(0,1)的随机值。将经过动态对立学习的种群适应度与标准算法种群适应度进行对比,选择较优的种群作为初始化种群,具体如式(13):

2)自适应收敛因子。
基本的鲸鱼优化算法中,收敛因子e呈线性变化,线性递减的收敛因子会造成算法在前期搜索较慢、后期求解不精细,不利于算法区分全局搜索和局部搜索。为平衡全局搜索与局部搜索,采用非线性函数替代e,如式(14)所示的Sigmoid 函数[17]常被用作神经网络的激活函数,具有前期下降快和后期下降较慢的特点。

为增强算法的全局搜索和局部寻优能力,将Sigmoid函数引入到收敛因子中。
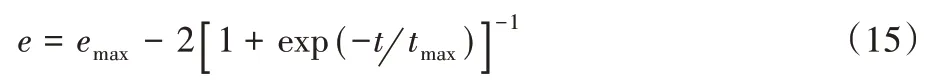
式中emax为收敛因子设定的最大值。基于Sigmoid函数重新定义了收敛因子的变化率,使收敛因子的值随迭代次数的增加呈非线性减小。在算法迭代的初期,e减小较快,有利于全局搜索,可以更全面地发现多个潜在极值,进而快速地进行全局搜索;而在后期,随着迭代次数的增加,e的变化率逐渐减小,算法在局部搜索时可以对最优解进行更精细化的搜索。
3)动态权值因子。
动态权值因子的变化能够影响算法的全局勘探能力和局部寻优能力。为进一步提高算法的收敛速度和精度,结合控制参数e的动态变化,在局部位置更新中引入了和非线性收敛因子e同步变化的自适应权值w,并添加了自适应权值系数η,具体操作如式(16)所示:

本文将权值w的表达式设置为w(t)=e,算法搜索阶段的迭代次数t→tmax时,对算法的位置更新,采用动态权值因子,使权重能够跟随适应度的变化调整权值,算法的求解精度和收敛速度在寻优过程中进一步改善,有利于算法跳出次优解。
2.2 算法时间复杂度分析
本文所提的IWOA 主要是由对立学习种群初始化、自适应收敛因子和动态权值因子组成。当种群数目为N、优化问题的维度为D时,初始化种群的计算复杂度为O(ND);在鲸鱼位置更新环节,计算复杂度为O(ND)。因此每一次迭代过程中,算法的计算复杂度为O(2ND),近似为O(ND),等于WOA的复杂度O(ND)。表1中给出了GA、PSO、WOA及IWOA的计算复杂度。

表1 不同算法的计算复杂度Tab.1 Computational complexities of different algorithms
由表1 可知,四种算法的计算复杂度由种群数目N和优化问题D的维度决定,当优化问题的维度较高(D≫N)时,四种算法的计算复杂度都为O(ND),属于同一数量级。
2.3 算法性能测试
为了验证IWOA 的性能,本文选取了单峰、多峰和固定维度的9 个基准优化问题如表2 所示,其中:F1~F4 为高维的单峰基准函数,F5~F7 为高维的多峰基准函数,F8~F9 为固定维的多峰基准函数。单峰函数用于测试IWOA 的收敛速度和求解精度,多峰函数用于测试IWOA的全局探索能力。
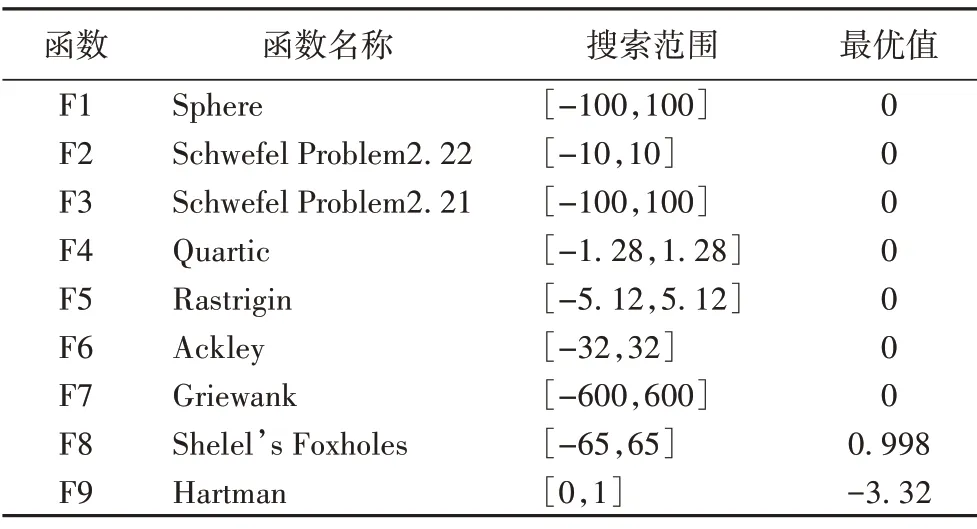
表2 基本测试函数Tab.2 Basic test functions
为研究算法在不同维度下的性能,F1∼F7 在实验中分别设置D=10,30,50。由于F8∼F9 为固定维度函数,不参与多维度测试,利用WOA 和IWOA 分别对每个测试函数独立运行20次,记录各个测试函数寻优的平均值,实验结果如表3 所示,其中加粗字体表示效果最好的结果。

表3 不同算法寻优性能比较Tab.3 Optimization performance comparison of different algorithms
由表3的结果可知,在单峰函数F1~F4上IWOA 的求解精度明显高于WOA,随着维度D由10增加到30和50时,目标函数趋于复杂,提高了WOA 求解的难度,IWOA 和WOA 求解精度有所下降。在多峰函数F6~F7 的求解上,添加了动态收敛因子和权值的IWOA 能够更加精确地求解函数最优值,具有较高的求解精度和鲁棒性。另外,在固定维多峰函数上,IWOA 同样取得了更优的解。通过以上结果对比验证了改进算法在全局寻优上的有效性。
2.4 基于IWOA的SVM参数优化
SVM 被广泛应用于分类和回归预测问题上,是由Vapink[18]在1995 年提出的,其基本原理和推导见参考文献[18]。对于给定的样本集,为了避免SVM 在学习训练的过程中,主观选择惩罚系数c和核参数g导致算法性能不佳,如核参数的值过小会导致支持向量机相互影响较大,预测精度降低,核参数过大则无法保证模型的推广能力[19]。利用WOA求取优化问题的优势,将IWOA应用在SVM参数寻优,进一步提高SVM模型性能。IWOA-SVM模型伪代码如下。
输入 目标函数,鲸鱼群参数。
输出 最优个体位置参数。

3 实验与结果分析
3.1 数据来源与评价标准
本文选取两个模型分别进行验证:
第一组数据 采用UCI 机器学习数据库中2017 年11 月明尼阿波里斯市交通流量数据进行实证研究。数据模型包含温度、降雨量、降雪量、乌云量,采样周期为1 h,共720 条数据。
第二组数据 采用文献[20]中国内某路口的2011年10月25日至10月27日3天的7:00—19:00 的某交叉路口交通数据流量集,数据模型仅包含交通流量,采样周期15 min,共144条数据。
采用平均绝对误差(Mean Absolute Error,MAE)和平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)作为算法测试的评价标准。
1)MAE定义为:

2)MAPE定义为:
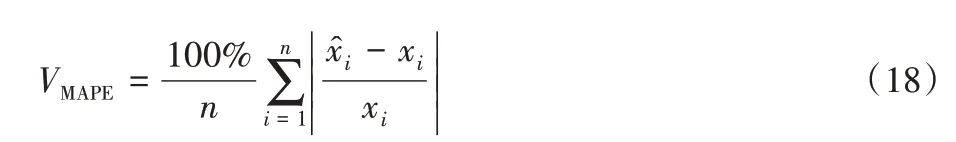
3.2 交通流量预测
3.2.1 第一组数据实验对比
首先,对第一组交通流预测采取多因素预测,利用SVM建立的回归模型对交通流量进行回归拟合,其中参数选择分别经GA、PSO、WOA 及IWOA 优化得到的最佳参数c和g对SVM 进行训练,得到GA-SVM、PSO-SVM、WOA-SVM、IWOASVM 模型,再对原始数据进行预测,得到11 月30 号数据预测结果如图5所示。
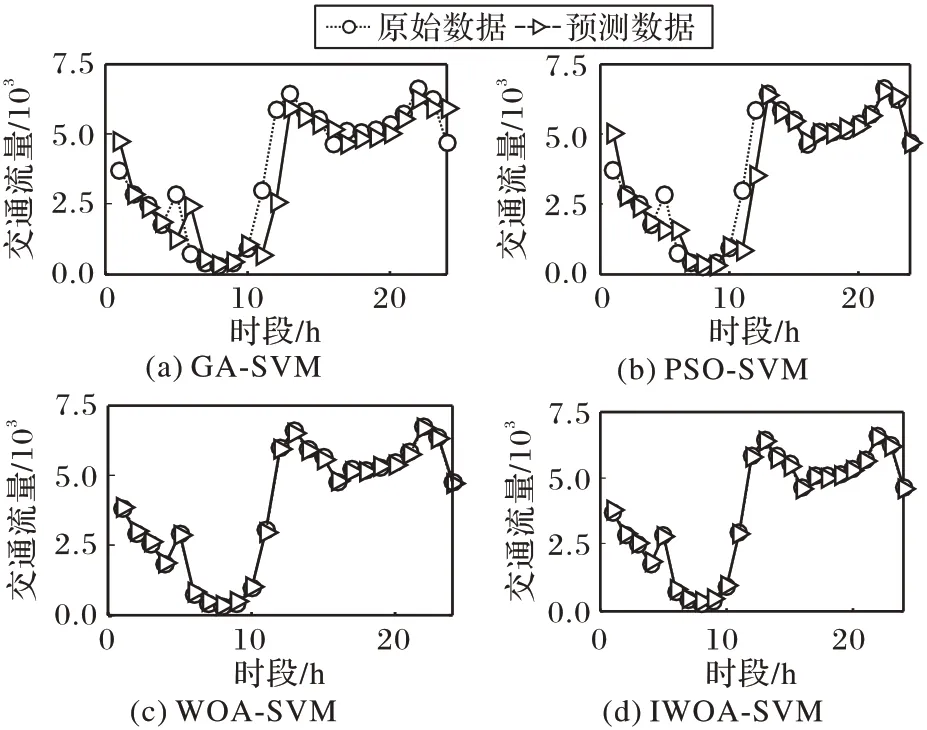
图5 第一组交通流量预测结果Fig.5 Prediction results of the first group of traffic flow
由图5 可以看出,IWOA-SVM 模型对于大部分训练样本都能进行很好的拟合,其预测精度较高,IWOA-SVM 模型具有较强的寻优能力。各个模型MAE 和MAPE 对比如表4 所示,可以看到IWOA-SVM性能最好。
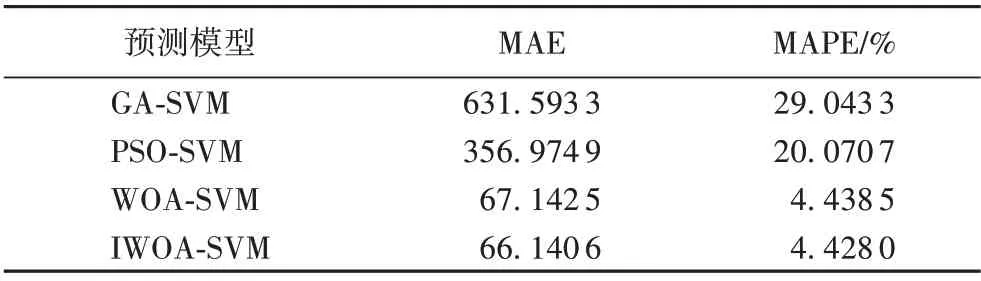
表4 第一组交通数据实验性能对比Tab.4 Experimental performance comparison of the first group of traffic data
3.2.2 第二组数据实验对比
对第二组交通流量数据进行预测,各个模型结果对比如图6 所示,MAE 和MAPE 对比如表5 所示,其中时间段ID 间隔为15 min。
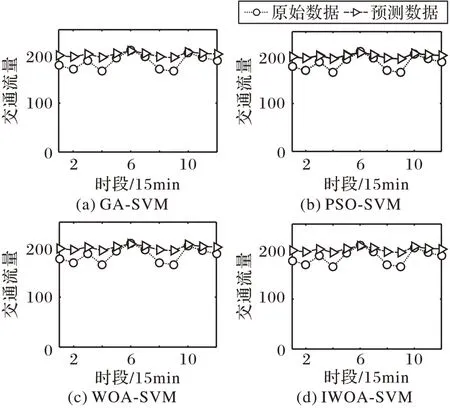
图6 第二组交通流量预测结果Fig.6 Prediction results of the second group of traffic flow

表5 第二组交通数据实验性能对比Tab.5 Experimental performance comparison of the second group of traffic data
由于第二组数据量较小且数据模型仅包含交通流量,各个模型预测性能差别较小,从对比图中不易看出区别,但从表5中可以看出,IWOA预测精度略优。
3.3 交通流量区间预测
为进一步对交通流量发生趋势和变化空间进行预测,采用FIG方法对交通时间序列进行处理,具体步骤如下:
步骤1 FIG 建立,对采集到的交通数据以1 h 为时间间隔建立交通时间序列窗口X=(x1,x2,…,xn),并选取粒度窗口大小o。
步骤2 确定三角形模糊集的核d、三角形模糊集的上界a和下界b。
步骤3 根据式(2),交通流量经过FIG,分别得到交通流量的下限Low 部分、交通流量上限Up 部分和描述交通流量平均水平的R部分。
对Low、Up 及R 三个部分进行预测能够进一步判断交通流量发生趋势和变化空间。
3.3.1 第一组数据实验对比
对第一组国外11 月份交通流量使用FIG 后的数据如图7所示,其中窗口大小o=6,24 h 数据序列被划分为6 个窗口。通过图7 可以看到,720 组数据经过模糊窗口粒化后分为了120组数据,粒化后的3个部分能够针对性地描述交通流量变化区间和趋势。
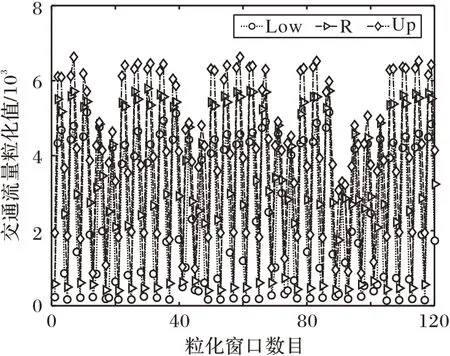
图7 第一组交通流量模糊粒化结果Fig.7 The first group of traffic flow fuzzy granulation results
根据FIG 结果,分别利用FIG-GA-SVM、FIG-PSO-SVM、FIG-WOA-SVM、FIG-IWOA-SVM 模型来预测以上3个成分(区间上界,区间下界和趋势成分),实际范围值和预测范围值数据格式为[Low,R,Up]。其中4 组数据序列为1 天,11 月28、29、30 日共3 天的数据用于验证所建模型的泛化能力。不同模型的交通流量变化趋势和空间预测对比如表6所示。
从表6 可以看出,对于测试样本,FIG-IWOA-SVM 模型预测趋势和变化区间最接近实际交通流量范围值,GA和PSO优化的FIG-SVM 模型对交通流量区间的预测与实际交通流量变化区间相比误差较大。在描述交通流量发生趋势R值的第1、5、9组数据预测上,FIG-GA-SVM 模型和FIG-PSO-SVM 模型预测精度较低,与FIG-WOA-SVM 和FIG-IWOA-SVM 模型相比,预测精度不平稳,难以满足交通流量预测的需要。FIGIWOA-SVM 泛化能力较强,在多种交通流量预测上精度均高于其他三种模型。为了更加直观地了解FIG-GA-SVM、FIGPSO-SVM、FIG-WOA-SVM、FIG-IWOA-SVM 四种模型预测精度,在表6 的基础上计算了四种模型的预测相对误差百分比,结果如表7所示。
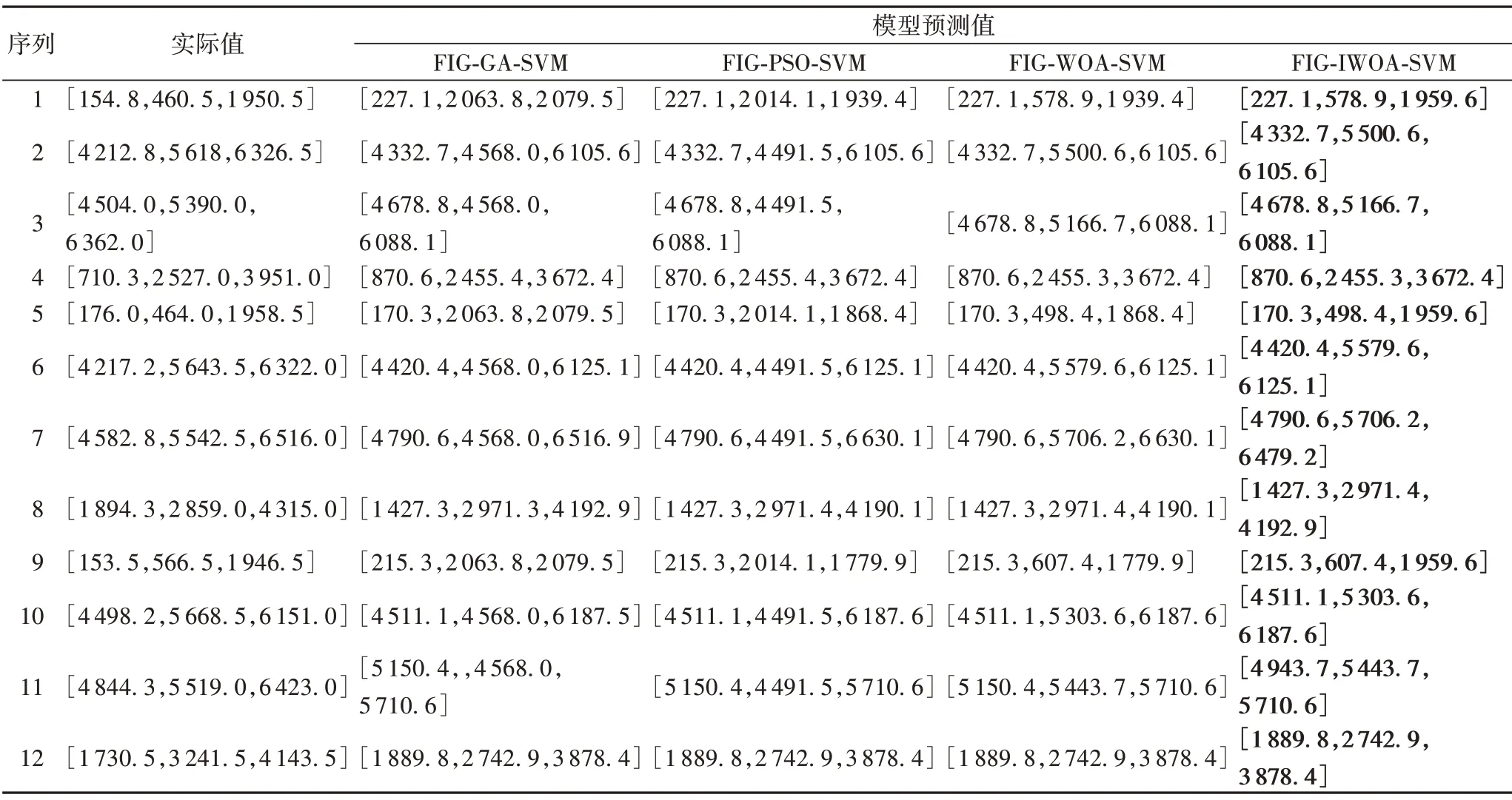
表6 第一组交通流量变化趋势和变化区间预测Tab.6 Change trend and change interval prediction of the first group of traffic flow
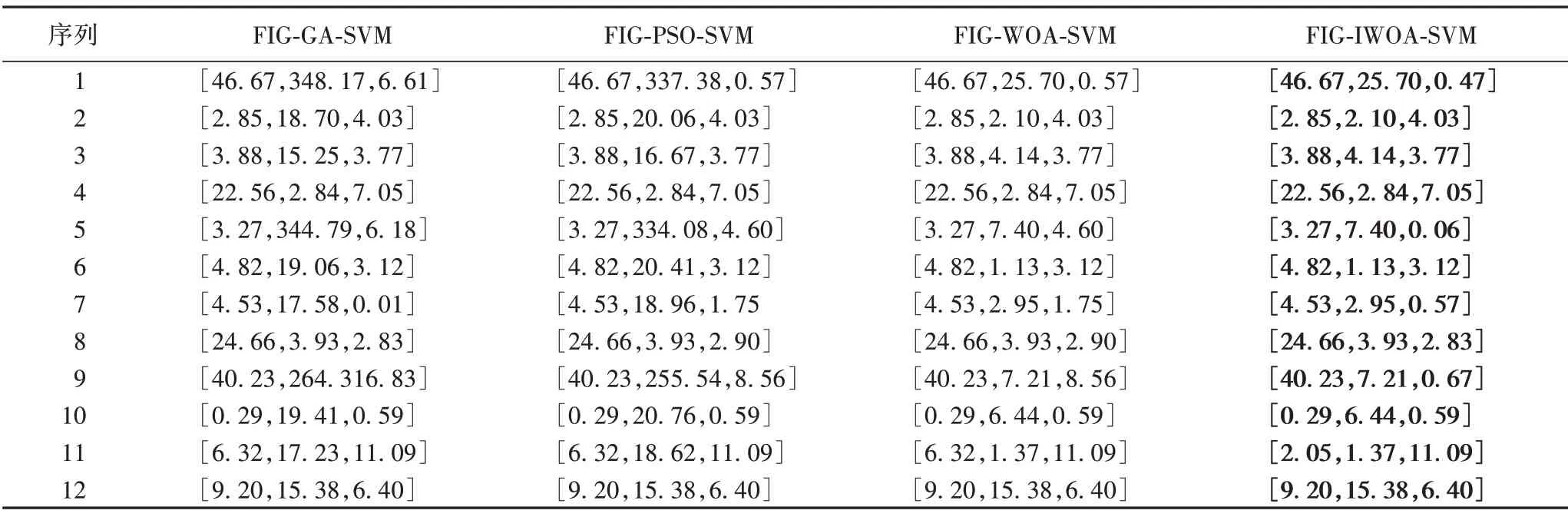
表7 第一组交通流量变化趋势和变化区间预测误差 单位:%Tab.7 Change trend and change interval prediction error of the first group of traffic low unit:%
通过表7 可以看出,在预测描述交通流量区间的下界值时,四种模型预测精度相差较小,但在预测描述交通流量的趋势值R 和区间的上界值Up 时,FIG-IWOA-SVM 模型和FIGWOA-SVM 模型相较于FIG-GA-SV 模型和FIG-PSO-SVM 模型相对误差较低,表明WOA 能够更加精确地找到SVM 模型的最优参数。FIG-IWOA-SVM 模型对WOA 进一步优化,在交通流量区间下界值Low 中的第11 组数据精度大于FIG-WOASVM,对于趋势值R 预测两个模型精度相同,而在描述交通流量的Up 上界值上,FIG-IWOA-SVM 模型在1、5、7、8、9 组数据上精度均优于FIG-WOA-SVM模型。
3.3.2 第二组数据实验对比
对第二组11月份国内某路口交通流量使用FIG后的数据如图8 所示,其中窗口大小为o=4,1 h 数据序列被划分为1个窗口。可以看到,144 组数据经过模糊窗口粒化后分为了36组数据。
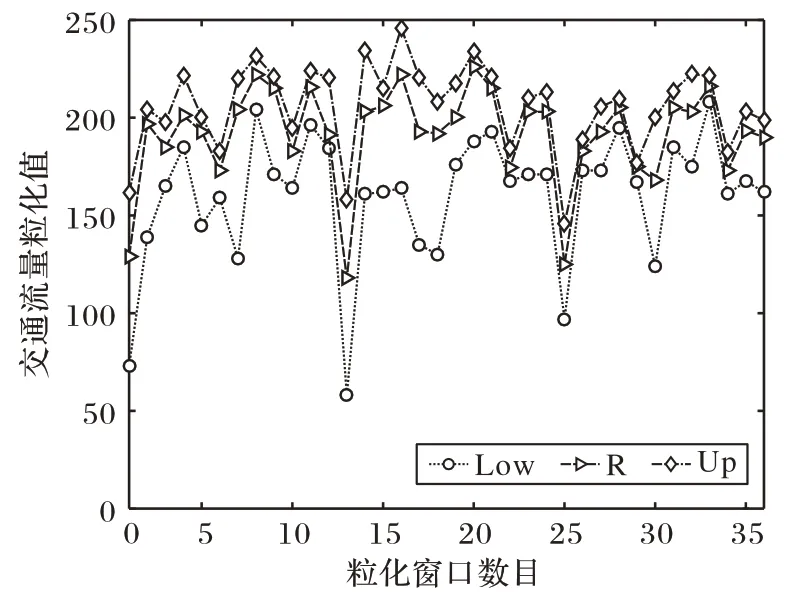
图8 第二组交通流量模糊粒化结果Fig.8 The second group of traffic flow fuzzy granulation results
根据FIG 结果,分别利用四个模型来预测交通区间,数据格式为[Low,R,Up],其中12 组数据序列为1 d,10 月27 号18:00—19:00 的数据用于验证所建模型的泛化能力。不同模型的交通流量变化趋势和空间预测对比如表8 所示,交通 流量变化趋势和空间预测误差如表9所示。

表8 第二组交通流量变化趋势和变化区间预测Tab.8 Change trends and change interval prediction of the second group of traffic flow

表9 第二组交通流量变化趋势和变化区间预测误差 单位:%Tab.9 Change trend and change interval prediction error of the second group of traffic flow unit:%
由表8 可以看出,FIG-IWOA-SVM 模型预测交通流量更接近于实际交通流量,其中,使用FIG-GA-SVM 和FIG-PSOSVM 模型预测的Low 值与实际Low 值误差较大,R 值部分中除第一个数据外,4个模型预测值相同,Up部分中四个模型预测值较为接近。由表9 可得,FIG-IWOA-SVM 模型预测误差最小。
总体上,FIG-IWOA-SVM 模型预测值较为平稳、精度更优,进一步验证了IWOA 的有效性,表明该模型能更加精确地预测交通流量的变化趋势和区间。
4 结语
为了对交通流量变化趋势和范围进行预测,本文提出了改进鲸鱼优化算法优化支持向量机的交通流量模糊粒化预测模型。通过动态对立学习、自适应权重及动态阈值对WOA的恒定权重进行了改进,提高了WOA 的预测精度,并在9 个测试函数上进行性能测试验证了IWOA 的优越性。同时,对交通流量信息模糊粒化,建立了多因素影响下的交通流量区间集合。最后,通过两种实际算例对交通流量变化区间进行预测,实验结果表明,所提FIG-IWOA-SVM 预测精度更高。下一步工作将围绕大规模路网下的交通流量变化空间和趋势预测,并将区间预测和短时预测相结合进一步提高算法的实用性。
