动力定位深海采矿船作业过程数值分析
2021-11-05朱枭猛郭兴乾
朱枭猛 李 彬 郭兴乾
(1.中国船舶及海洋工程设计研究院 上海200011;2.上海船舶工艺研究所 上海200030)
0 引 言
近半个多世纪以来,世界经济高速增长,矿产资源的消耗引发新的问题。受现实条件所迫,人类将能源资源开发的新希望聚焦于海洋。海洋矿产资源主要分布在大洋底部,目前探明具有商业开发前景的有多金属结核锰结核、富钴结壳和热液硫化矿床以及生物基因资源等,丰富的海洋矿产也将成为难以取代的接替资源而为人类所开发和利用,开发大洋矿产资源已经成为世界各国发展的战略目标。
姚丽琳通过CFD方法研究了大型设备深水安装过程中若干时刻的船-缆-体耦合系统运动响应。张万里利用Moses采用非线性时域耦合分析方法对入水及下放阶段进行模拟。赵梦一等基于工作安全分析与作业条件危险性评估法对水下设备下放过程进行风险分析,建立了下放安装风险评估体系。
海底采矿过程中,采矿船利用动力定位(DP)系统保持位置及艏向。DP系统主要控制船舶低频运动,数值模拟中考虑DP过程将影响其运动特性。
目前主要研究成果中,对采矿作业中船舶动力定位过程的分析尚不充分,且数值模拟中计及DP过程影响的研究较少。主要解决以上两个问题。本文首先建立采矿船、扬矿立管、扬矿中继站以及环境载荷的数学模型,采用集中质量法对立管进行动态分析;然后建立船舶动力定位系统模型,本文主要涉及控制器及推力分配单元。在采矿船动力定位过程中,对组合体系统进行时域耦合数值模拟,计算得到船舶及水下设备运动时历、推进器推力时历和立管张力等信息,研究了船舶与水下设备运动相互作用效果。结果显示DP过程对船舶、立管及水下设备动力响应均产生影响,因此深海采矿设计分析中对船舶动力定位过程的模拟具有重要意义。
1 采矿系统数学模型
深海采矿系统模型如图1所示,包括采矿船、立管、扬矿中继站以及ROV集矿机等,ROV与中继站通过软管连接,假设其对系统其他部分运动影响很小并且可以忽略。因此本文重点对船-立管-体耦合部分进行分析。
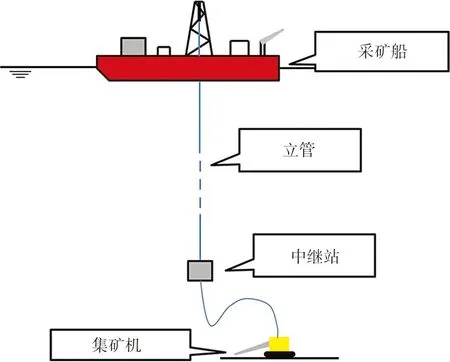
图1 深海采矿系统概念模型
本文计算物理量均采用基于m、kg、s的国际单位制,以使各模型物理量量纲协调,其中深海采矿船的运动方程为:
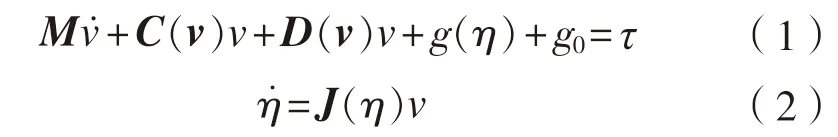
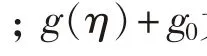
风、浪、流为船舶在海上作业过程中的主要环境载荷。一阶波浪力影响船舶波频运动,二阶波浪力、风力、流力和推进器推力影响船舶低频运动。DP系统为避免过度损耗,重点响应低频运动。
一阶波浪力采用三维辐射绕射势流理论进行求解。规则波流域速度势为:
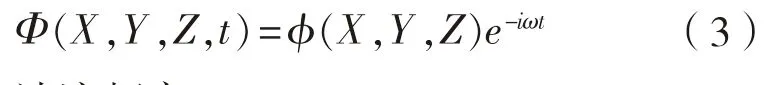
ω
为波浪频率。根据文献[8],有:

式中:、分别是入射势和绕射势;为六自由度单位速度势,表示浮体运动对流场扰动的贡献。根据速度势,流体作用力通过表面压力积分获得:
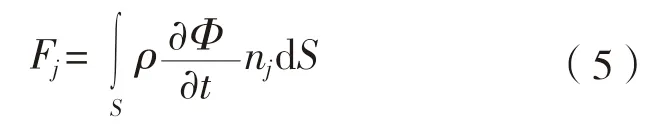
ρ
为水密度,kg/m;n
为面元法向,S
为平均湿表面积,m。不规则波认为是若干规则波的叠加,设规则波数为N
,ω
、a
分别为波谱中各规则波频率与波幅,f
为与之对应的Froude-Krylov力和绕射力,ε
为随机相位角,则一阶波浪力的计算公式为: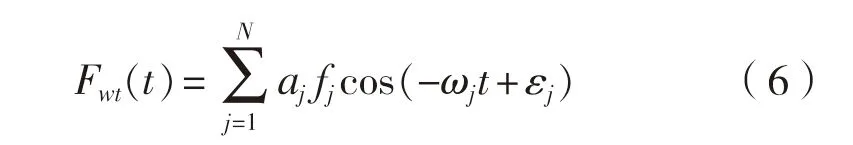
采用二次传递函数计算二阶波浪力,忽略和频力,根据Newman近似有二阶波浪力计算公式:
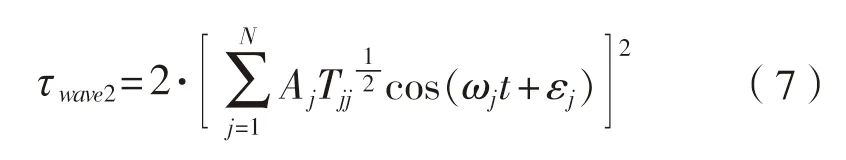
T
为传递函数。风、流载荷采用OCIMF规范推荐方法进行计算 [10]:
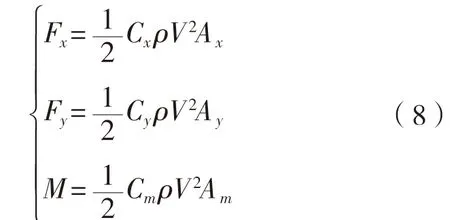
C
、C
、C
为风/流载荷系数;ρ
为风或海水密度,kg/m;V
为相对速度,m/s;A
、A
、A
为受载部分投影面积,m。扬矿立管采用集中质量法进行动态分析,即假设管线由若干集中质量点和无质量直线段杆元组成。杆元仅模拟杆轴向和扭转特性,质量、重力、浮力以及流体作用力等均集中作用于杆元两端节点处。杆元两端建立随体坐标系Sx
y
z
和Sx
y
z
,节点处建立随体坐标系Nxyz
,如图2所示。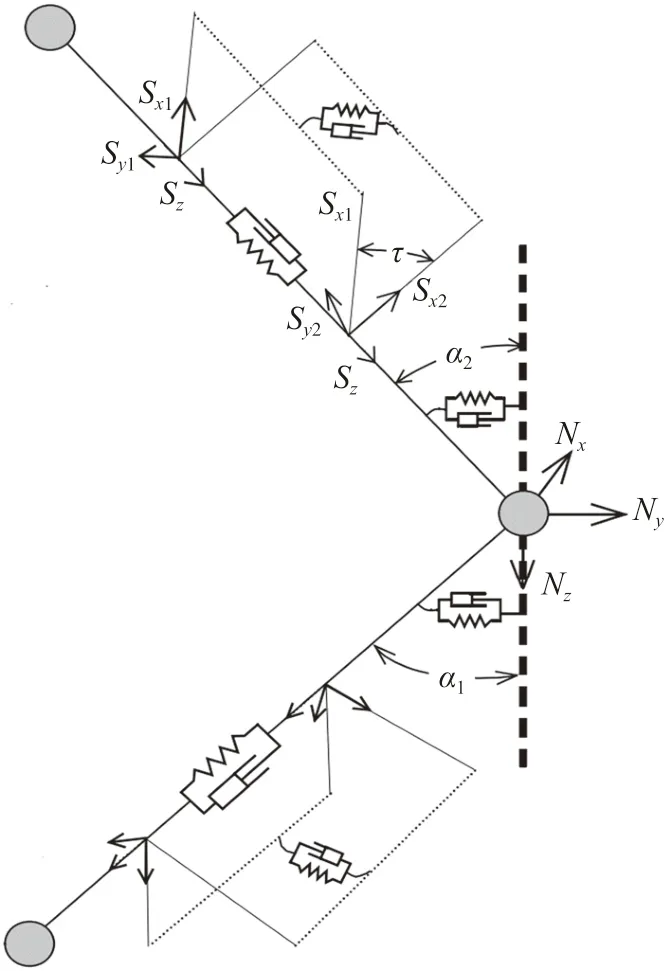
图2 杆单元模型
杆元中轴向弹簧阻尼单元的有效张力为:
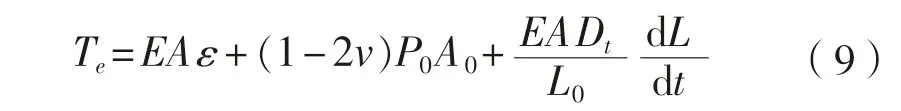
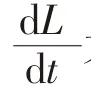
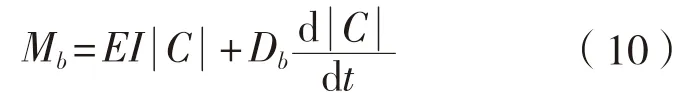

杆元扭矩为:
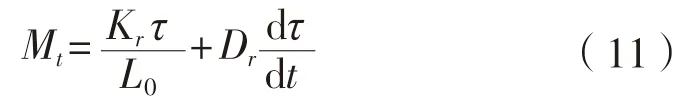
K
为扭转刚度;τ
为扭转角;L
为单元初始长度;D
为扭转阻尼。作用于管线的阻力采用Morison方程求解。相对于管线的流速V
可以分解为垂直于管线轴线的V
和平行于管线轴线V
,其中V
还可以进一步分解为V
与V
。这样,阻力可以分解为三个方向分量,即F
、F
、F
,对应的阻力系数分别为C
、C
、C
。则三个方向的流体阻力分别为: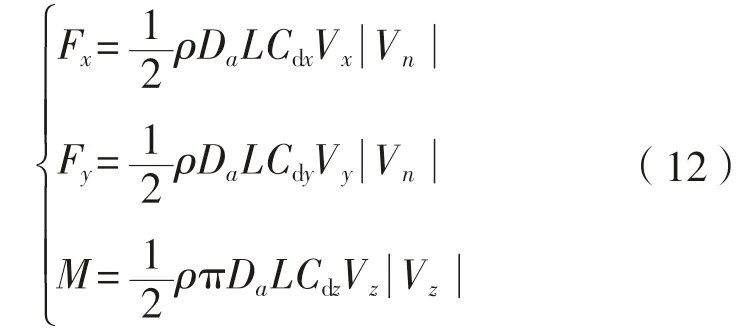
ρ
为流体密度,kg/m;D
为管直径,m。附加质量的影响通常在局部x
、y
、z
方向上分别计算,对于每个方向管元受管加速度引起的额外惯性力和周围流体加速运动的作用力。各方向附加质量作用为: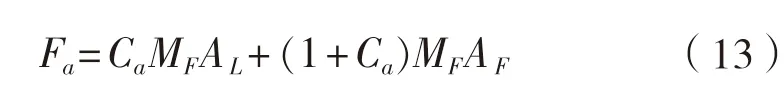
C
为该方向附加质量系数;M
为流体质量,kg;A
为该方向管加速度分量,m/s;A
为该方向流体加速度分量,m/s。水下扬矿中继站设备具有刚体六自由度运动,其运动方程为:
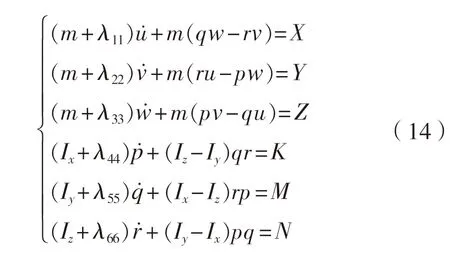
m
为设备质量;λii
为附加质量;u
、v
、w
和p
、q
、r
,分别为设备线速度(m/s)和角速度(rad/s);X
、Y
、Z
和K
、M
、N
,分别为各自由度设备所受的力(N)和力矩(N·m)。设备受水阻力根据Morison方程计算。水面采矿生产支持船、扬矿立管、水下扬矿中继站设备组成深水采矿系统,该系统的运动方程为:
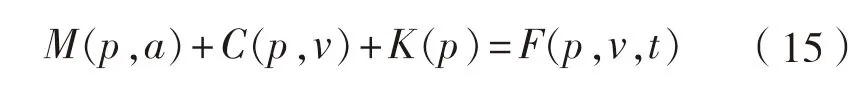
M
为系统惯性力;C
为系统阻尼力;K
为系统刚度力,p
、v
、a
分别为位置、速度和加速度;t
为时间。本文采用广义α
法通过隐式迭代求解系统动力方程。2 动力定位系统
为适应深水采矿作业需求,采用具有DP功能的采矿船。在进行深海采矿时域模拟中,综合考虑船舶DP过程对研究船、管、水下设备之间运动影响、张力影响,以及推进器推力具有实际意义。
DP控制系统采用PID控制器:
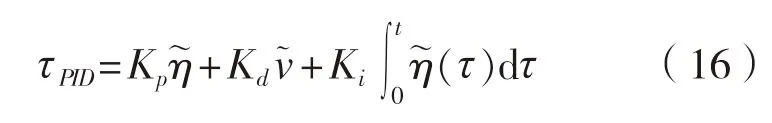
K
、K
、K
分别为控制参数。动力定位系统主要对船舶低频运动进行控制,本文采用时间离散Kalman滤波对船舶运动信号进行处理,获得低频运动状态。DP船舶的运动系统通常是过驱动的,一般将推力分配转化为最优化问题来求解。目标是在各推进器发出所需总推力和力矩的同时达到最低的能源消耗,同时减小机械磨损。推力分配目标函数为:
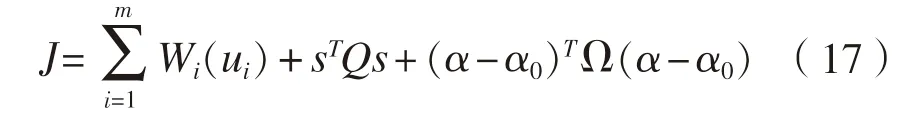
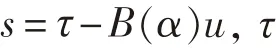
动力定位系统具有7台推进器,其中5台为全回转推进器,2台为槽道推进器。推进器的布置如图3所示。
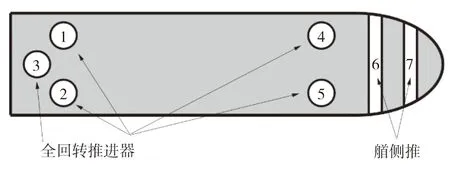
图3 采矿船推进器布置
3 深海采矿时域模拟
采矿船的主尺度以及主机推进器配置参数分别如下页表1所示;立管主要参数如下页表2所示;中继站尺寸为4 m×4 m×6 m,重30 t;主要环境参数如下页表3所示。
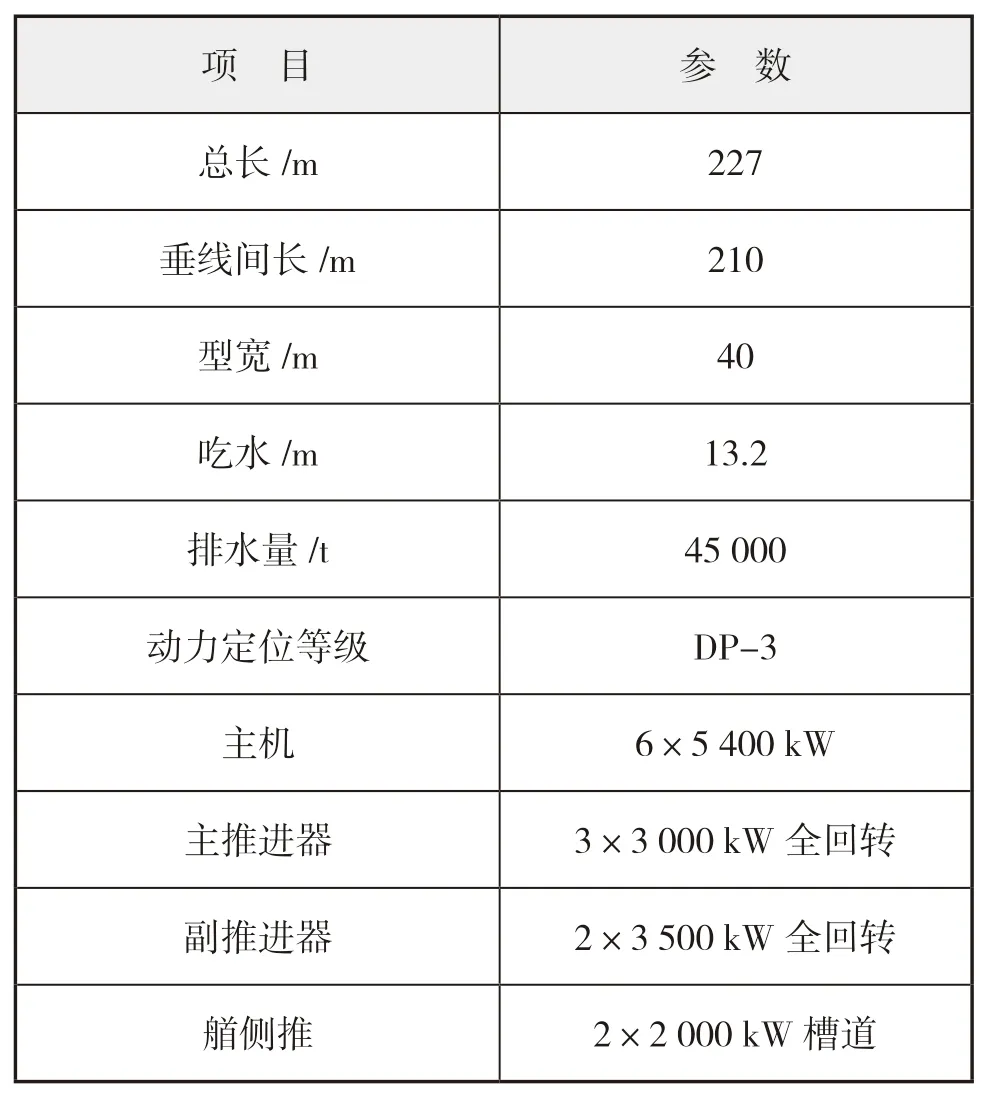
表1 采矿船主尺度参数
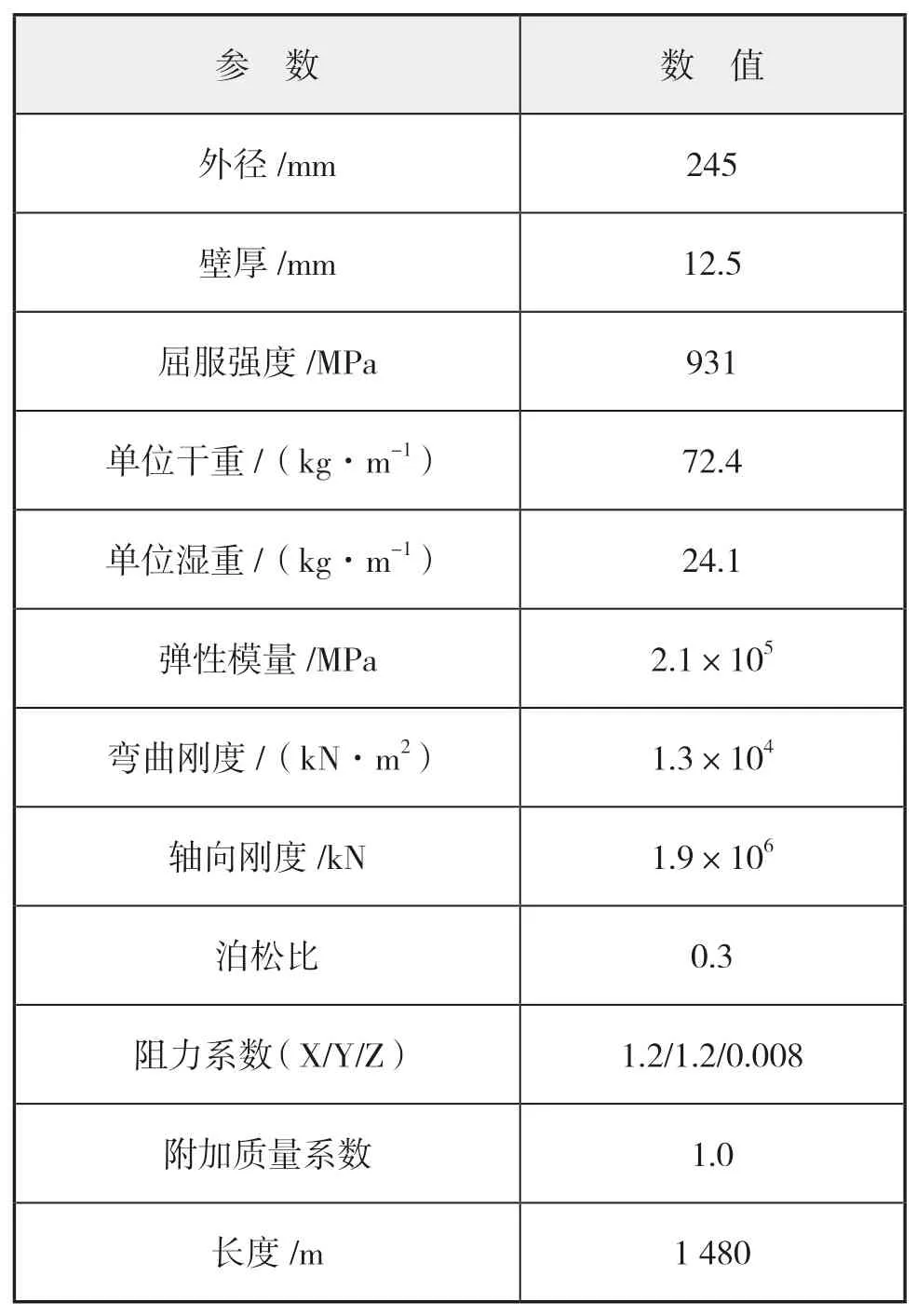
表2 立管主要参数
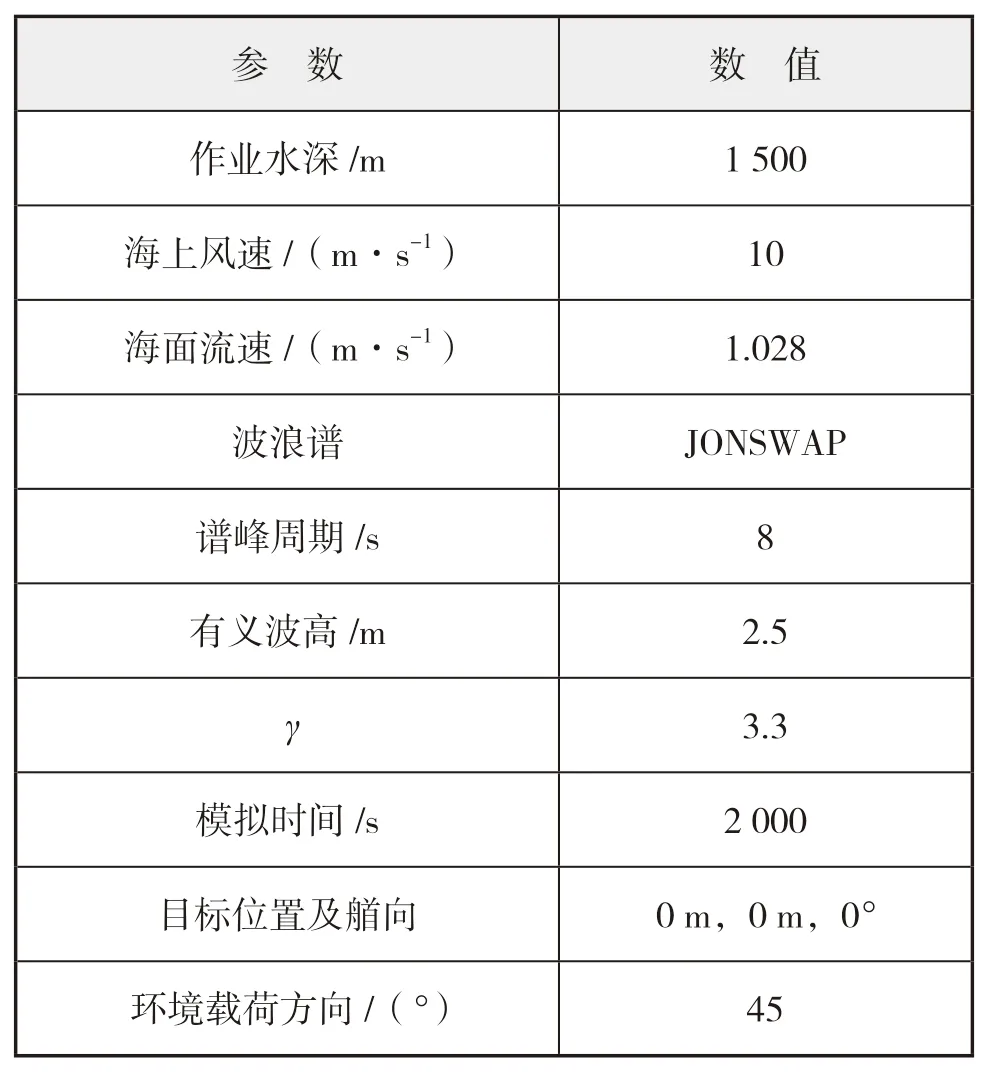
表3 主要环境参数
基于以上数学模型及参数,对深海采矿过程进行时域模拟。分析过程如图4所示。如图在模拟过程中,采矿船处于动力定位状态。通过数值计算获得船、立管及设备的运动及受力信息,以及推进器推力信息等。
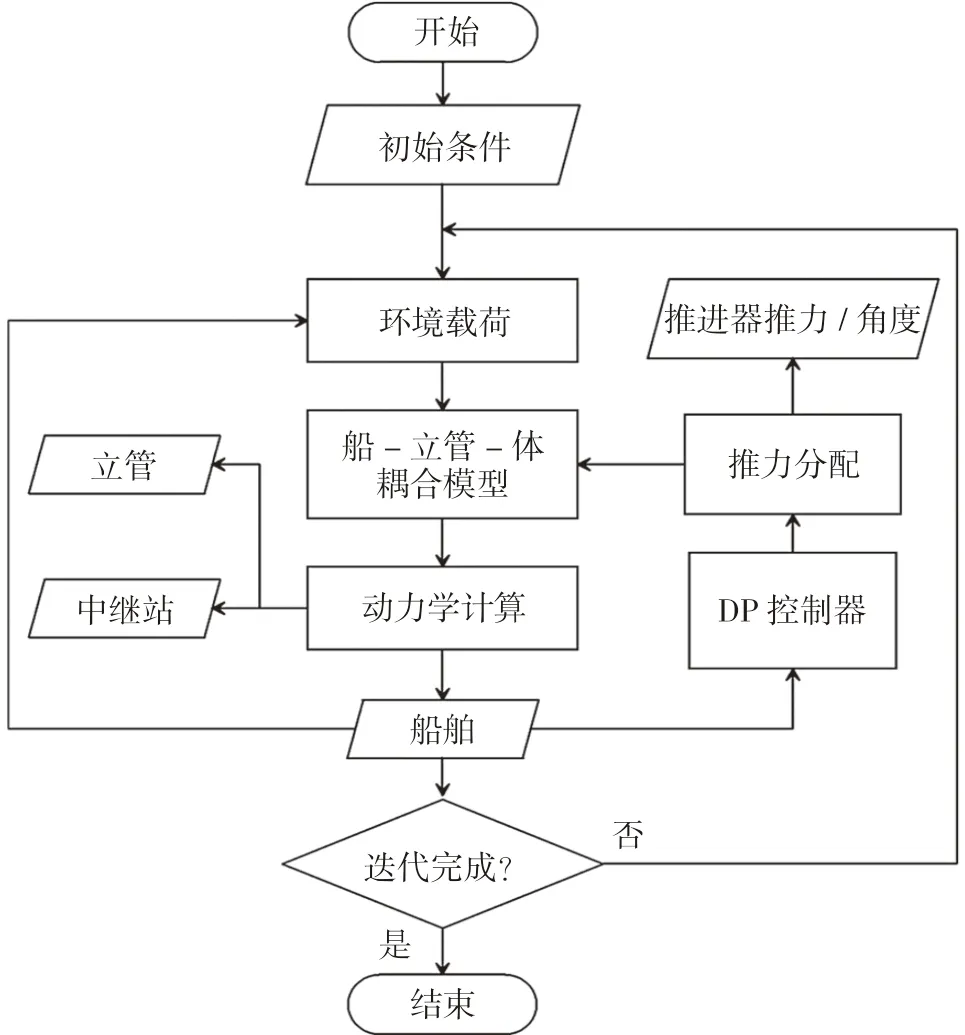
图4 数值分析流程图
4 计算结果与讨论
4.1 计入动力定位对浮体运动动态分析的影响
在采矿船系统进行深水采矿作业期间,采矿船利用动力定位系统保持其在海面上的工作位置。采矿船的目标位置如表3所示,位于地球固定坐标系中。图5展示了采矿船在本文所设置的作业工况下的六自由度运动时历曲线。
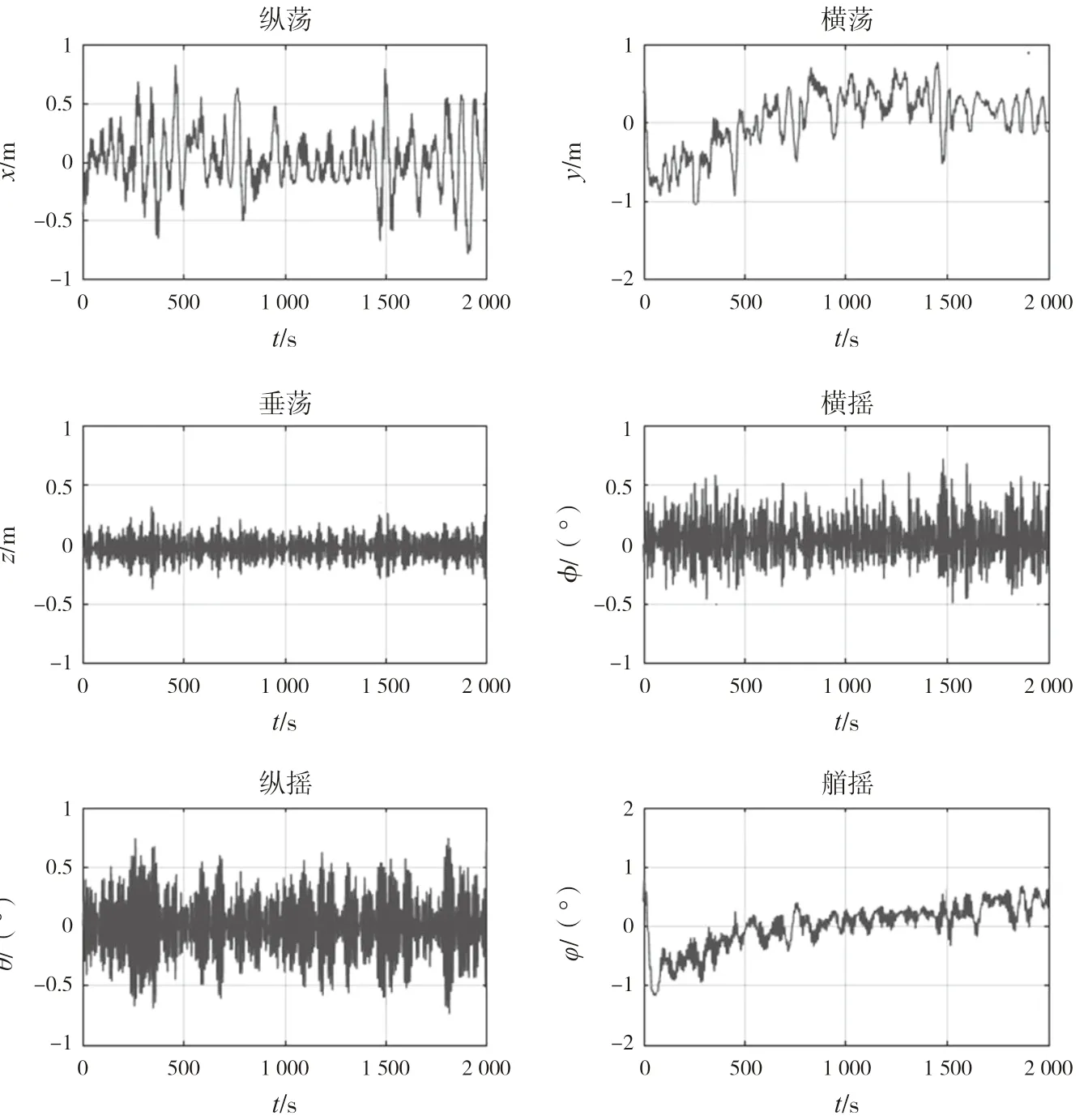
图5 作业中采矿船运动过程
船舶初始状态为(0 m,0 m,0°)。模拟初始阶段环境载荷的突然切入造成船舶运动产生较大响应,DP系统随之产生较大推力,过程中船舶横向及艏向发生较大位移。结合图8可知船舶水平方向由低频运动主导,DP及低频环境载荷对船舶运动造成更大作用。通过图中的纵荡、横荡和艏摇图可以发现,动力定位系统能够保持采矿船的水平位置和艏向。采矿船动力定位系统可以达到2 m和2°的定位精度。图5中还展示出了动力定位过程中的采矿船垂荡、纵荡和横荡的动态响应,计算结果中可以看出这3个自由度运动受波频载荷影响。
下页图6给出了设计工况下水平方向3个自由度的推进器总控制力。结果显示推进器的推力工作频率较低,符合动力定位系统的工作工作状态特点。动力定位系统的控制力具有一定余量,系统具有足够的定位能力承受环境载荷。数值模拟结果也验证采矿船动力定位系统模型的有效性。
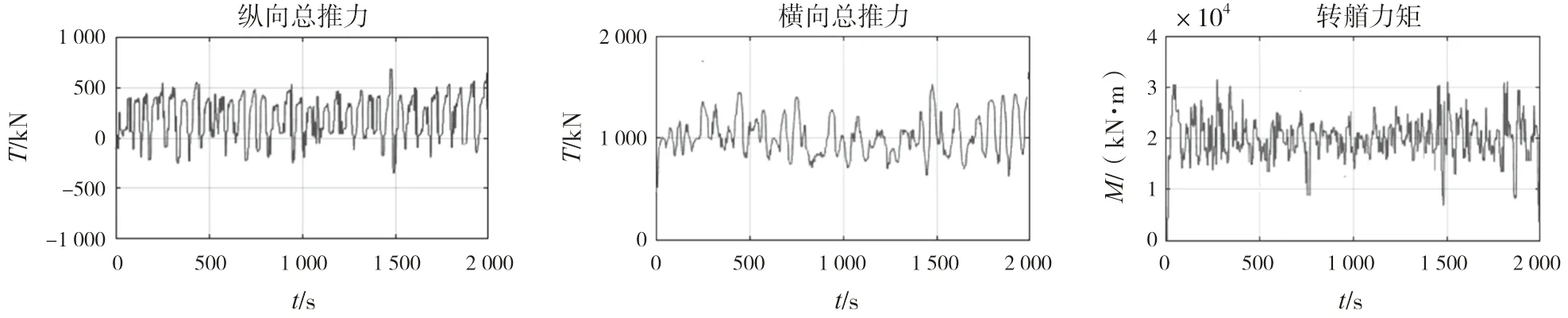
图6 推进器总推力
若浮体运动数值模拟中不考虑动力定位,则其运动由RAO计算,并在平衡位置附近振荡。为了在没有动力定位作用时能够保持位置,此时需忽略慢漂运动。下页图7展示了不考虑动力定位作用的浮体六自由度运动曲线。其中水平面三自由度的运动规律与考虑动力定位时的情况明显不同。
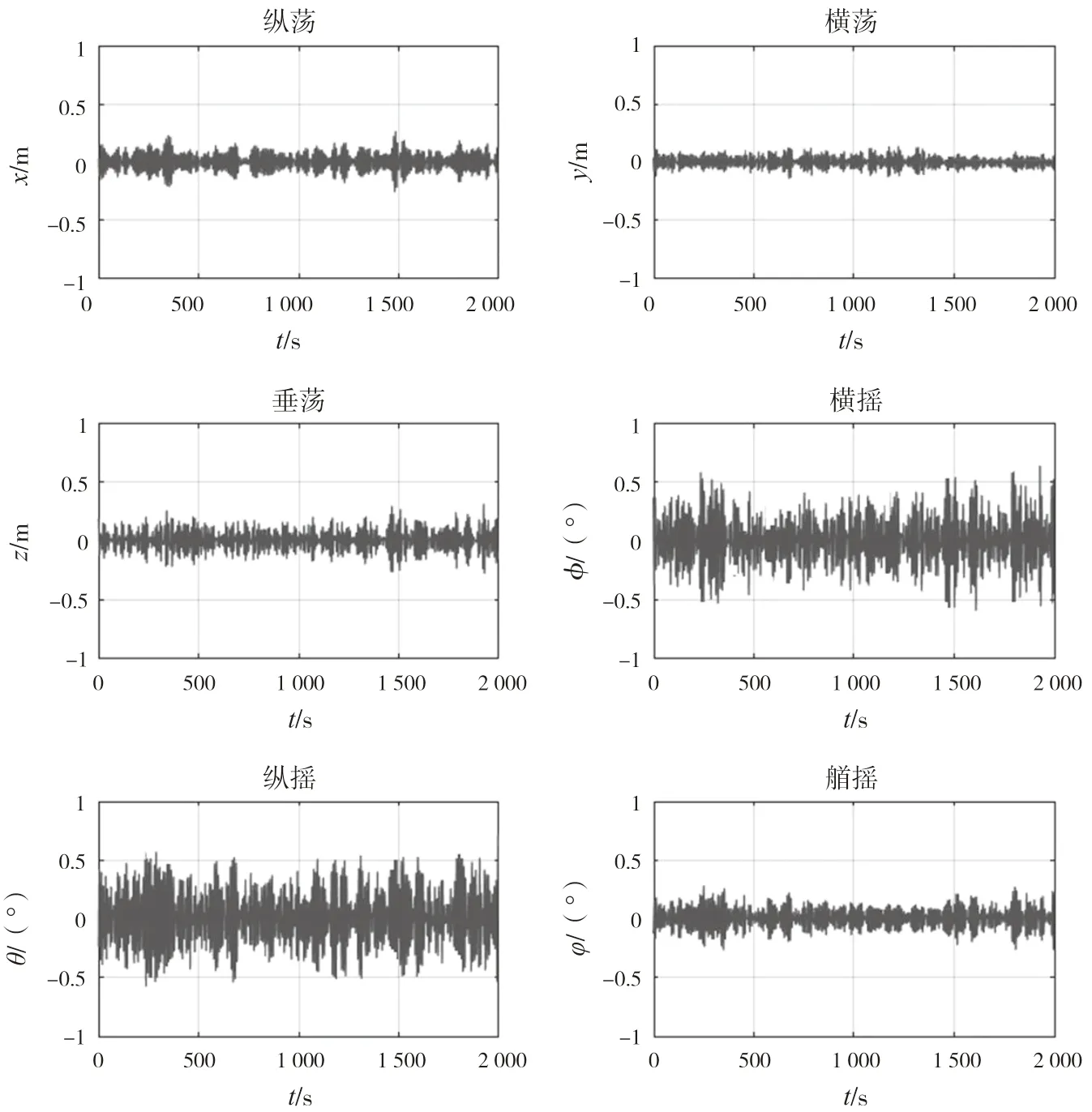
图 7 不考虑动力定位作用下船舶运动
为了对比浮体运动响应,下页图8分别展示了六自由度运动功率谱曲线。图中实线表示计入动力定位的数值模拟结果,虚线表示不考虑动力定位的数值模拟结果。对比显示,不计入动力定位作用时数值模拟忽略低频的漂移运动,没有低频响应。计入动力定位作用并考虑低频运动后,浮体水平运动在低频段响应占主要部分,响应幅度整体强于不计入动力定位的情况。而根据特征值分析,其共振频率与浮体低频响应频率吻合,低频响应容易造成立管系统弯曲振动响应。因此,忽略低频运动响应则忽略了浮体运动对立管系统弯曲振动响应。忽略动力定位作用能够引起数值模拟中船舶垂荡响应偏低,响应频率偏高。此外,忽略动力定位定位作用使横摇响应偏高,纵摇响应偏低。

图8 采矿船运动响应对比
综上,对于深海采矿系统运动过程数值模拟,动力定位系统模型对浮体运动数值模拟产生影响,动力定位作用不可忽略。
4.2 计入动力定位对立管和设备动态分析的影响
深海采矿系统运动过程数值模拟中,计入动力定位系统模型后,浮体运动响应特征受到影响,水平面运动在动力定位控制下的低频响应占主要部分。水面浮体的运动响应影响立管张力与设备运动。为了研究数值模拟中考虑浮体动力定位作用对立管的影响,图9展示了深海采矿系统中立管张力的对比。对比显示,水面浮体运动响应的差异引起立管动态张力响应差异。
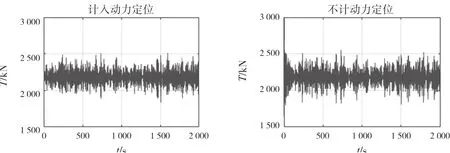
图9 立管张力对比
下页图10为立管张力功率谱,对比表明,不考虑动力定位作用时采矿系统运动过程数值模拟中立管张力响应更大。这主要是由于水面浮体低频响应部分的增强,使得波频响应部分相对减弱,即使计入动力定位模型后浮体垂荡响应更大,然而其水平面运动则主要为低频运动,各自由度运动耦合后使数值模拟中立管张力响应降低。
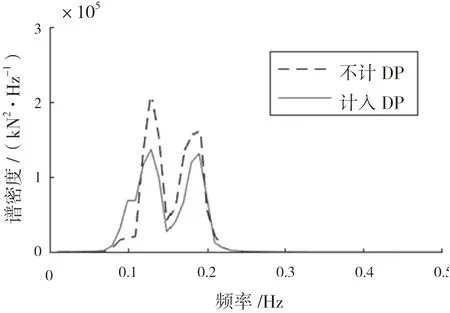
图10 立管张力响应功率谱对比
动力定位模型的计入最终将引起设备运动受到影响。图11展示了设备垂荡,图12为设备垂荡功率谱。对比发现,考虑动力定位作用时数值模拟中设备垂荡响应变小,主要响应频率变小。图10与图12呈现双峰现象,一方面由于立管受船舶波频运动影响,另一方面由于垂向的激励造成立管出现一定轴向共振现象。
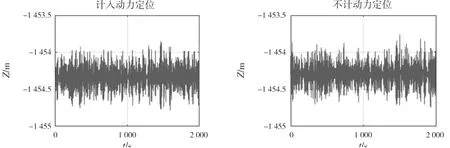
图11 设备垂向运动对比
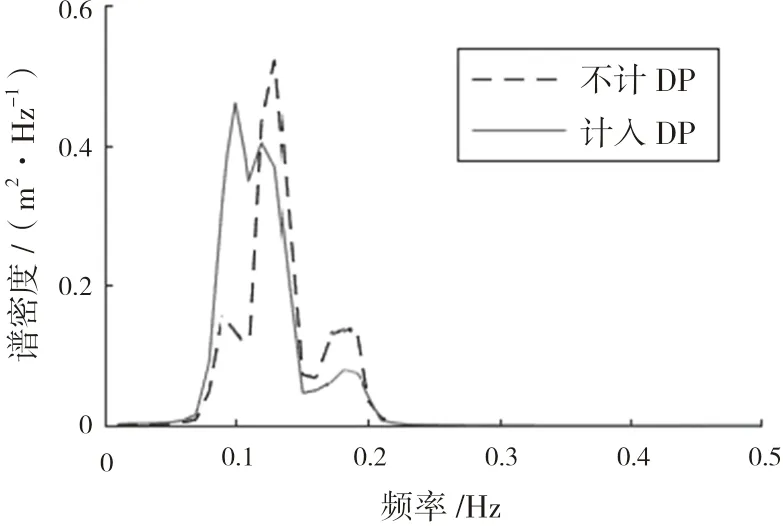
图12 设备垂荡功率谱对比
4.3 计算方法验证
为了保证本文所述方法在深海采矿系统动力学计算中的准确性,与文献[15]模型实验结果进行了对比验证。该试验研究了顶部受迫振动的竖直立管动态响应规律。其中立管模型采用特氟龙和聚乙烯制成,顶端固连于运动机构,通过传感器测量顶部受力,底端连接重物,整体在静水中竖直悬吊。利用水下摄像机观测横向位移。实验装置如图13所示,主要参数如下页表4所示。
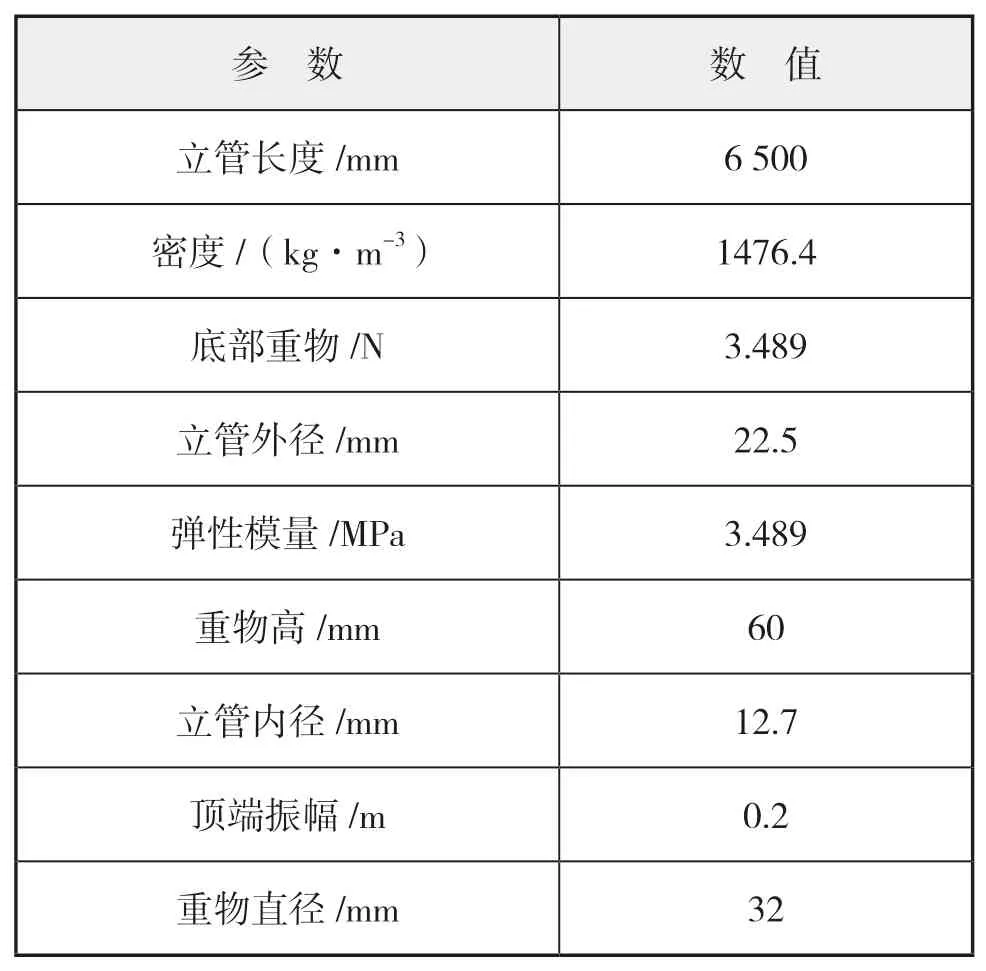
表4 模型试验主要参数
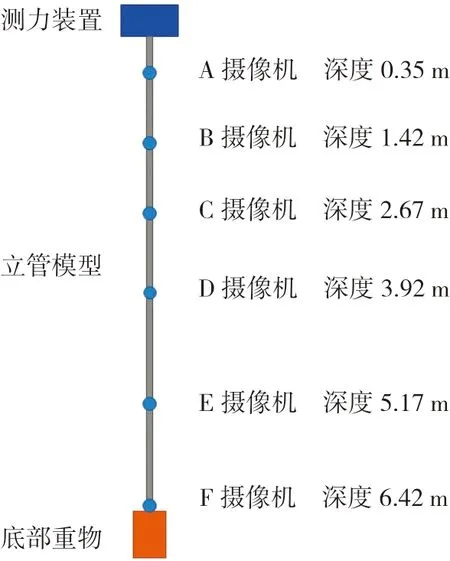
图13 立管试验装置
模型顶端进行水平受迫正弦运动,振幅0.2 m,取不同频率试验。稳态响应时,底部与上部有相同的运动周期。下页图14~17分别选取了周期5 s与13 s的位移及张力结果对比曲线,可知本文计算方法能够良好吻合试验结果,即验证了该方法在应用于此类模型的准确性,能够适用于深海采矿船系统的动力分析。
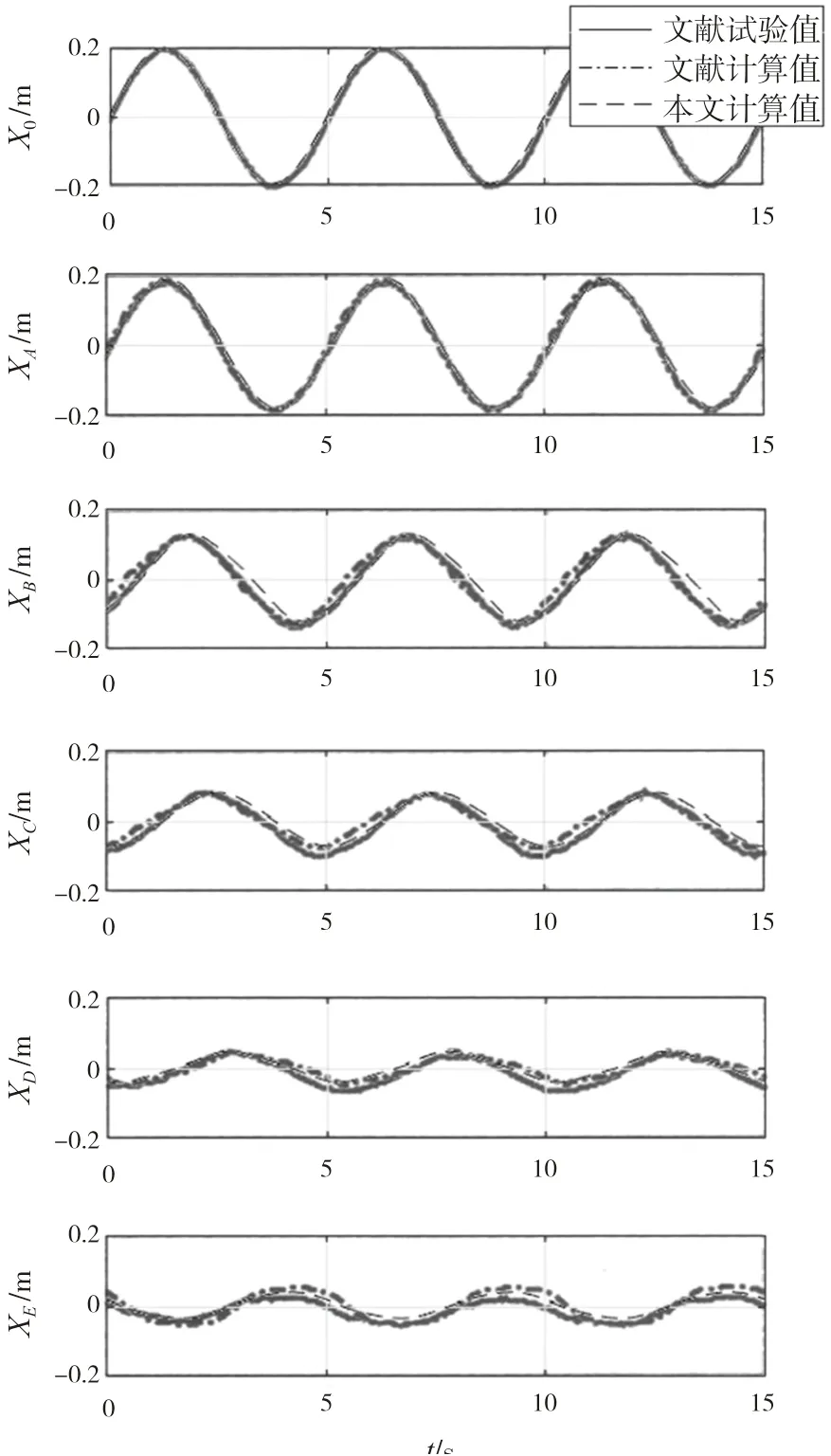
图14 周期5 s位移结果对比
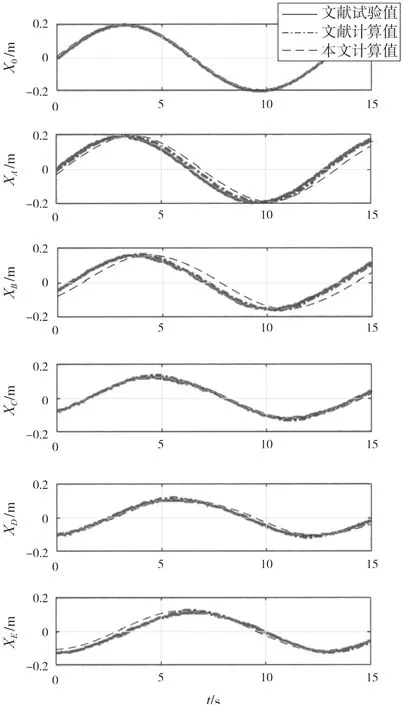
图15 周期13 s位移结果对比
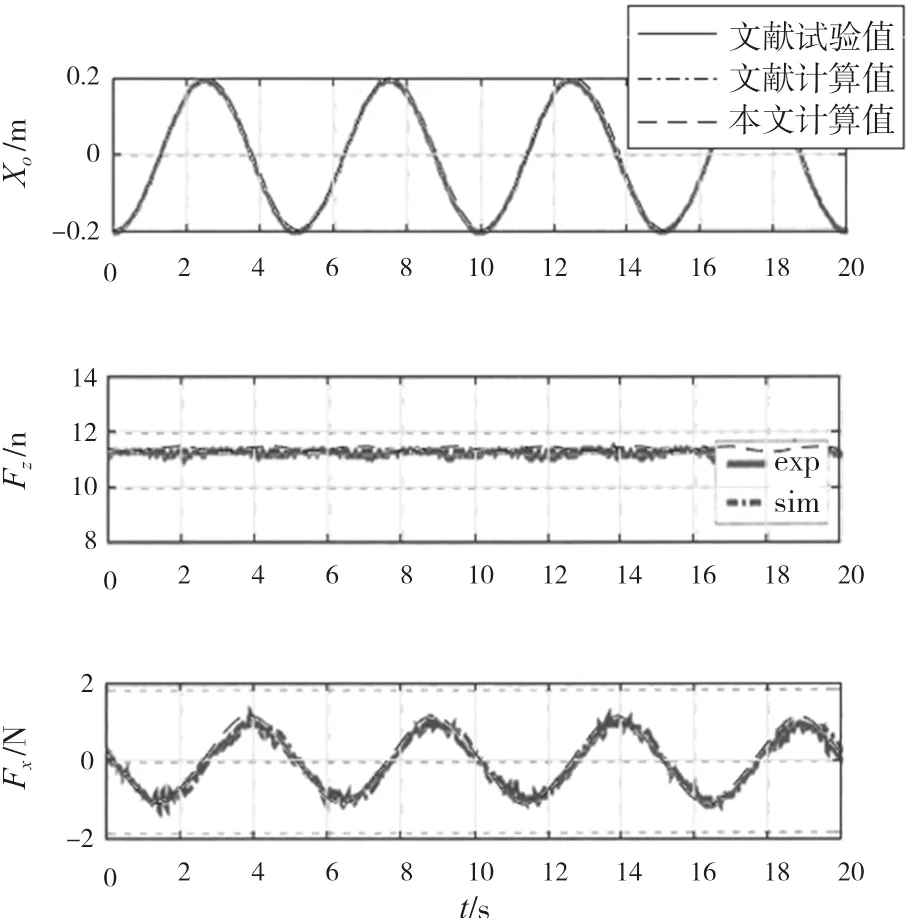
图16 周期 5 s顶端张力对比

图17 周期 13 s顶端张力对比
5 结 论
本文建立了深海采矿作业过程船-立管-体耦合运动系统分析模型,为采矿船配置了DP系统。并对DP作用下深海采矿系统运动过程进行时域耦合数值模拟,根据仿真计算结果,得到以下结论:
(1)本文提出数值模型能够对动力定位作用下深海采矿系统运动过程进行模拟;在指定环境条件下,DP系统具有足够定位能力以及良好定位精度;
(2)深海采矿过程动态分析中,动力定位系统模型对浮体运动数值模拟产生影响,动力定位作用不可忽略;
(3) 考虑DP作用后,各自由度运动耦合使数值模拟中立管张力响应降低;
(4)考虑DP作用后,数值模拟中设备垂荡响应变小,主要响应频率变小。
本文充分考虑了DP系统对采矿船-立管-设备组合体运动模型的作用,对深海采矿系统设计分析具有指导意义。
