LNG储罐泄漏的三角模糊事故树定量分析研究*
2021-11-05王文正贺辉宗厉建祥
王文正,陈 亮,贺辉宗,厉建祥
(中石化安全工程研究院有限公司,山东青岛 266104)
0 前言
液化天然气(LNG)作为世界公认的优质、清洁、高效能源,在我国能源结构中得到广泛的重视和利用。由于LNG本身具有的易燃易爆特性和严苛的储存运输条件,导致LNG一旦发生泄漏,尤其是LNG储罐泄漏,极有可能引发连锁事故效应,造成灾难性的后果。自1944年美国克利夫兰LNG储气站火灾爆炸事故以来,全球陆上有详细记载的20多起LNG罐区泄漏爆燃事故,均造成巨大的人员伤亡和财产损失。因此,加强LNG储罐泄漏致因的风险分析研究,对保障储罐的安全平稳运行具有重大的现实意义。Isaac A.对LNG储存、运输过程中的风险分析与评估研究进行了系统化综述。刘云鹏基于Bow-tie模型对液化天然气泄漏风险进行了深入分析,并结合保护层分析和风险矩阵对各类安全技术措施进行了评估。但是,目前开展的LNG储罐泄漏分析主要是基于传统事故树开展的定性分析,部分学者虽然对导致储罐泄漏的因素进行了定量研究,但未考虑基本事件的不确定性和概率的模糊性,受人为主观因素的影响较大。为此,模糊集理论被引入事故树量化分析当中,并得到广泛的认可和应用。孟凡亭等构建模糊事故树对液氨泄漏爆炸事件进行了模糊量化分析。Anjuman S.采用模糊Bow-tie法对油气管道开展了可持续性风险评估,分析了导致油气管道失效的相关因素。
为此,针对LNG储罐泄漏风险,通过构建三角模糊事故树,对导致LNG储罐泄漏的风险因素进行定量分析,并提出针对性的建议和措施,为LNG储罐的科学管理和平稳运行提供借鉴。
1 基于模糊集理论的事故树模型
1.1 事故树分析方法
事故树分析是以不期望事件作为分析对象,将系统各环节潜在的失效因素有机联系在一起,找出导致顶事件发生的所有可能原因和原因组合。基于构建的事故树,可以采用上行法和下行法求解事故树的最小割集。在不考虑各基本事件发生概率的情况下,可以计算基本事件的结构重要度,如式(1):

(1)
式中:F
(j
)——基本事件j
的结构重要度系数;n
——第r
个包含基本事件j
的最小割集的容量;k
——包含基本事件j
的最小割集的个数。1.2 模糊集理论
1.2.1 三角模糊数


(2)

选取具有线性特征的三角模糊数与事故树分析相结合,进行定量分析。隶属函数可表示为:
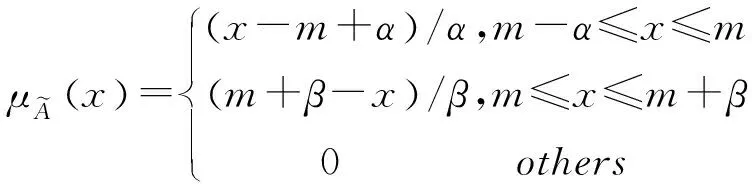
(3)

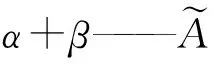
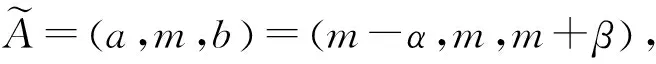
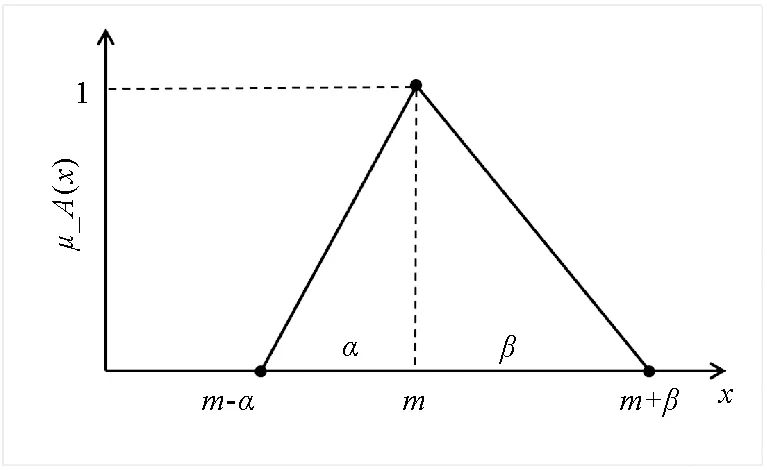
图1 三角模糊数隶属度函数
1.2.2 三角模糊数的运算
三角模糊事故树的计算过程与传统事故树类似,与门模糊算子和或门模糊算子分别为:

(4)

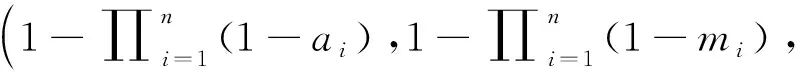
(5)


a
,m
,b
)——三角模糊数的下限、最可能值、上限参数;n
——计算因子个数。1.2.3 模糊重要度分析的中值法
假定三角模糊数隶属度函数中存在一点Z,且经过此点的分界线可以将三角面积等分,那么Z点就是该三角模糊数的中位数,则当α
<β
时存在: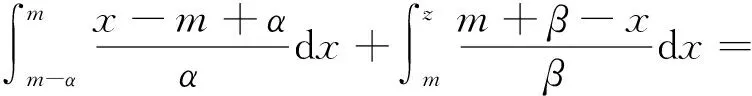
(6)
可求得:

(7)
当β
<α
时存在: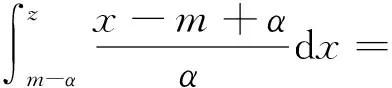
(8)
可求得:
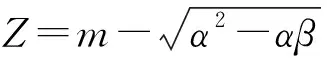
(9)

S
=T
-T
,(10)
比较分析各基本事件的模糊重要度S
,可得基本事件对系统的影响程度。2 LNG储罐泄漏的事故树建立与定性分析
2.1 LNG储罐泄漏的事故树建立
选取LNG储罐泄漏作为顶事件,从LNG储罐管线、罐体损伤、储罐附件、阀门、法兰、密封以及施工安装、维护管理、第三方破坏、自然灾害等方面自上而下开展逻辑分析,明确事故树的中间事件、基本事件及各事件之间的逻辑关系,建立LNG储罐泄漏的事故树,如图2,各符号代表的事件见表1。

表1 LNG储罐泄漏事故树中符号的意义
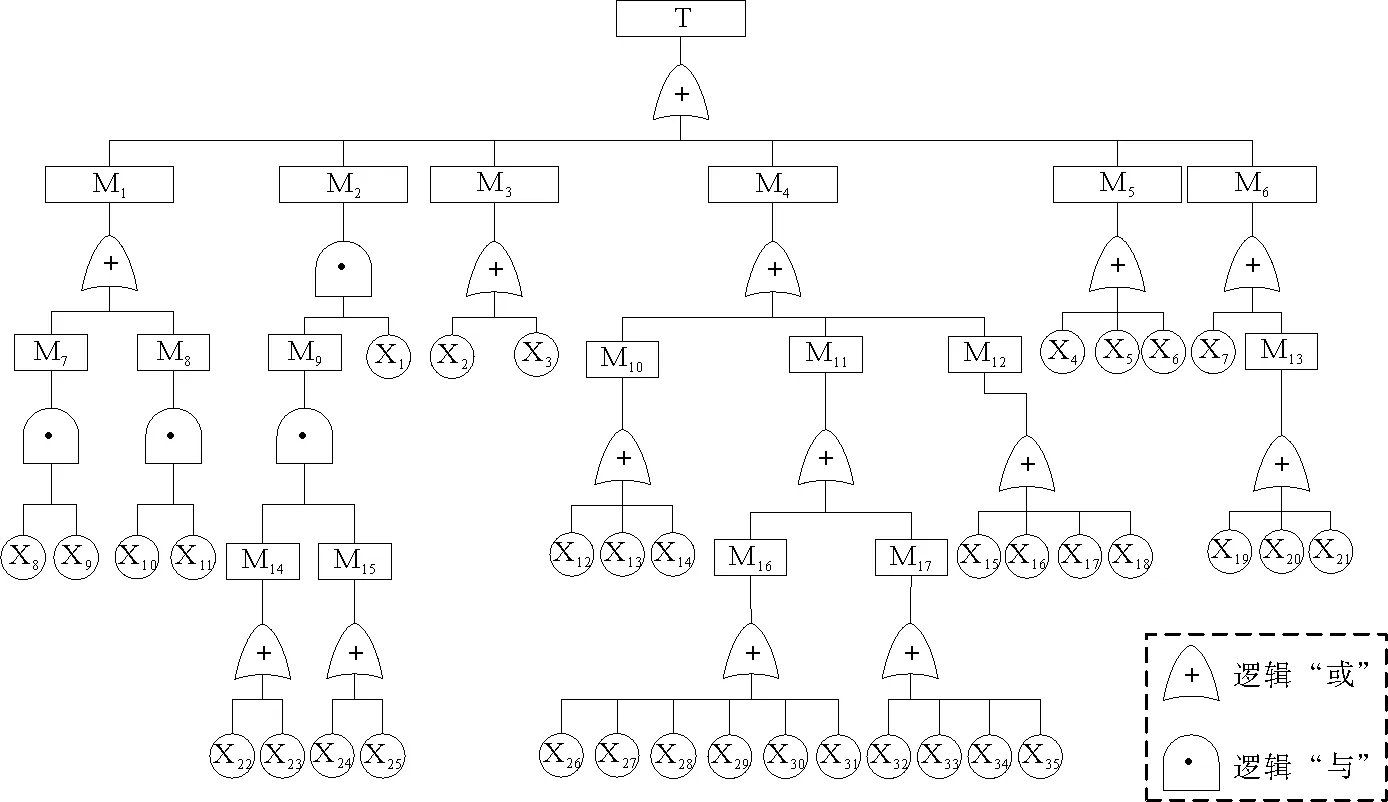
图2 LNG储罐泄漏事故树
2.2 LNG储罐泄漏事故树结构重要度分析
根据布尔运算采用下行法计算求解LNG储罐泄漏事故树,可得影响顶事件的最小割集为:X,X,X,X,X,X,X,X,X,X,X,X,X,X,X,X,X,X,X,X,X,X,X,X,X,X,XX,XX,XXX,XXX,XXX,XXX。其中包括26个1阶最小割集、2个2阶最小割集和4个3阶最小割集。
同时,在不考虑各基本事件发生概率的情况下,从事故树结构上计算各基本事件的结构重要度,分析各基本事件对LNG储罐泄漏发生的影响程度。经计算,各基本事件的结构重要度系数X=X=X=X=X=X=X=X=X=X=X=X=X=X=X=X=X=X=X=X=X=X=X=X=X=X=X>X=X=X=X=X=X=X=X。分析结构重要度可知,罐体损伤、法兰变形损坏、填料选择与安装相关基本事件的结构重要度相对较大,需要高度重视;安全管理和检修维护的规范有效也是造成LNG储罐泄漏的重要因素,自然灾害虽然不可控,但在储罐设计建设过程中可以增加安全防护,提升储罐抗自然灾害的能力。
3 LNG储罐泄漏事故树模糊量化分析
3.1 LNG储罐泄漏的模糊概率可能分布

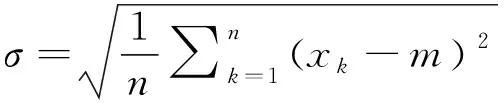
(11)
式中:m
——概率均值;σ
——概率标准差;x
——k
项估计值;n
——专家数。首先,基于OREDA、CCPS等数据库可直接获取X(雷击)、X(地震)和X(水灾)的发生概率,分别为7.240×10、8.520×10、7.240×10,并将其发生概率转化为三角模糊数。对于无精确概率统计的基本事件,组织6位专家对各基本事件概率进行评估,专家信息见表2。

表2 评估专家基本信息
在6位专家评估数据的基础上,对每个基本事件去掉最大值和最小值保留4个有效数据,再采用表征法对评估结果进行三角模糊处理,得到各基本事件的三角模糊概率值,见表3。
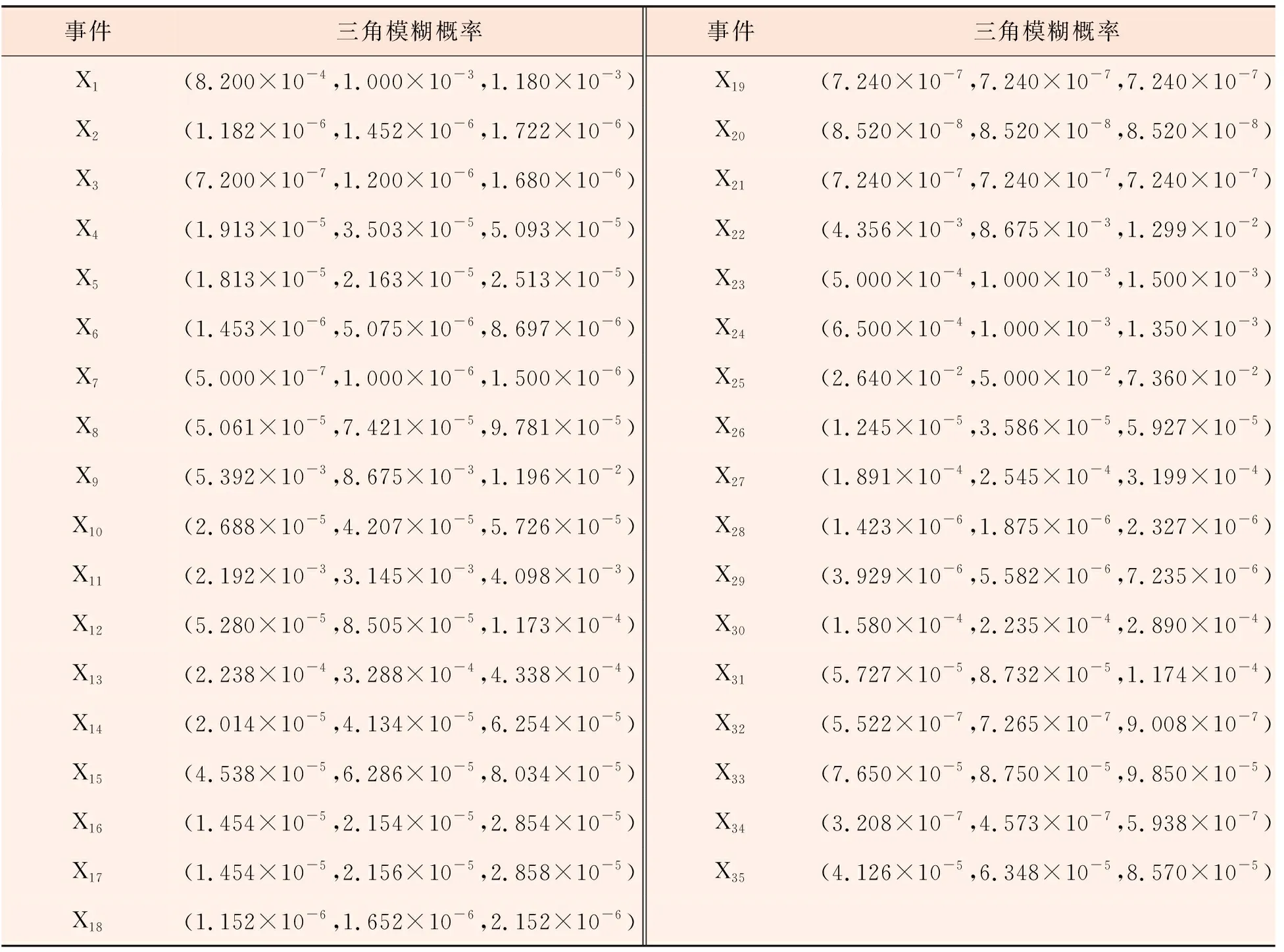
表3 LNG储罐泄漏基本事件的三角模糊概率
根据各基本事件的三角模糊概率,根据逻辑“与门”、“或门”模糊算子,计算获得各中间事件和LNG储罐泄漏的三角模糊概率,见表4。

表4 顶事件和各中间事件的三角模糊概率
分析表4可以看出,LNG储罐泄漏的三角模糊概率分布为(9.559×10,1.391×10,1.827×10),根据顶事件三角模糊数的核可知顶事件发生的概率为1.391×10,分析三角模糊数盲度可得顶事件发生概率波动范围为(4.351×10,4.360×10)。
3.2 LNG储罐泄漏的模糊重要度分析


图3 基本事件模糊重要度
分析图3可知,35个基本事件的模糊重要度区分明显,聚类后可分为第一区间“>1.0×10”、第二区间“1.0×10~1.0×10”、第三区间“<1.0×10”共3个区间。第一区间“>1.0×10”包括X(法兰垫片变形)、X(填料未正确安装)、X(操作不当)共3个基本事件,且X(法兰垫片变形)的模糊重要度最大,达到了3.2970×10,对LNG储罐泄漏顶事件的发生影响最为显著。第二区间“1.0×10~1.0×10”包含X(法兰结合处保温不佳)、X(压盖与阀杆间空隙过大或过小)、X(焊接不良)共14个基本事件,是导致顶事件LNG储罐泄漏的重要事件。第三区间“<1.0×10”包含X(填料超期)、X(排气系统未启动)共18个基本事件,其模糊重要度相对较低,对LNG储罐泄漏的发生影响相对较小。
同时,结合结构重要度分析结果以及各基本事件的三角模糊概率可以发现,虽然基本事件X、X、X、X、X、X、X、X的三角模糊概率都比较高,但由于上述基本事件与顶事件存在逻辑“与门”连接,导致相关事件的模糊重要度较低,处于第三区间。但是,这并不意味着可以放松对这8个基本事件的管控,其高三角模糊概率特征意味着相关事件的高频率发生,容易造成经常性违章和生产异常,应该重点关注。
4 建议措施
根据LNG储罐泄漏事故树的定性分析和定量分析,理清了LNG储罐泄漏的演化规律和各中间事件、基本事件的作用机制,提出有针对性的建议措施。
a) 分级开展LNG储罐泄漏风险管控。影响LNG储罐泄漏的35个风险因素可以聚类分为3个区间,风险因素个数分别为3、14、18。企业应根据导致LNG储罐泄漏的风险因素的模糊重要度和所在区间分类分级制定管控措施,重点关注第一区间中X(法兰垫片变形)、X(填料未正确安装)、X(操作不当)3个核心事件,合理分配资源。
b) 强化LNG储罐附件的本质安全设计与维护。法兰、填料室、阀体等LNG储罐附件的本质安全缺陷和维护保养不当是导致储罐泄漏的重要因素,企业在LNG储罐设计建造过程中要严格把关储罐附件的本质安全水平,投入运行后要重点关注储罐的日常维护保养。
c) 加强LNG储罐作业人员专业技能把关与培训提升。现场操作人员操作不当以及施工作业人员专业技能不足是导致LNG储罐泄漏的主要因素,企业在聘用新员工和选择承包商时应严格把关相关人员的教育背景和专业技能,不断加强专业技能培训和安全意识教育。
d) 关注高概率重点基本事件的发生。基本事件X、X、X、X、X、X、X、X自身的高概率特性容易造成经常性的生产异常,应该引起企业额外关注。
5 结论
通过建立LNG储罐泄漏的事故树演化路径,计算获得中间事件和基本事件的三角模糊概率和模糊重要度,并对导致储罐泄漏的风险因素定量聚类分析。
a) 归纳分析LNG储罐泄漏的风险因素,构建LNG储罐泄漏的三角模糊事故树,清晰地揭示了LNG储罐泄漏的原因和演化路径,并根据事故树结构开展了定性分析。
b) 基于模糊集理论和三角模糊事故树,计算获得LNG储罐泄漏和各中间事件的三角模糊概率,采用中值法求解各基本事件的模糊重要度,开展聚类分析获得各基本事件对LNG储罐泄漏发生的影响。
