非晶带材成型过程熔潭特性的数值模拟

张斐然 程舟济 潘永军

DOI：10.19850/j.cnki.2096-4706.2021.09.011

摘  要：平面流铸技术的出现为非晶带材中宽带的制取提供了可能，而位于喷嘴和铜辊表面之间熔潭的状态则决定了带材的性能和质量。通过对熔潭初始形成过程的数值模拟，详细分析了熔潭外形尺寸的变化及其内部温度场、速度场随时间的分布，进而推算出熔体的冷却速率这一制带关键参数。实验结果表明：在非晶带材的制取过程中，周围气体及熔潭内部出现的回流会影响到温度的表现，并计算出熔体的平均冷却速率为2.1×106 K/s，对比已有的实验结论，验证了该数值模拟的可靠性。

关键词：平面流铸;熔潭;温度场;速度场;冷却速率

中图分类号：TG249;TG244+.3               文献标识码：A 文章编号：2096-4706（2021）09-0038-04

Numerical Simulation of Molten Pool Characteristics in Amorphous Strip Formation Process

ZHANG Feiran，CHENG Zhouji，PAN Yongjun

（Wuhan Second Ship Design and Research Institute，Wuhan  430064，China）

Abstract：The appearance of planar flow casting technology makes it possible to produce wide strip in amorphous strip，and the state of molten pool between nozzle and copper roller surface determines the performance and quality of the strip. Through the numerical simulation of the initial formation process of the molten pool，the change of the overall size of the molten pool and the distribution of its internal temperature field and velocity field with time are analyzed in detail，and then the key parameter of strip making，the cooling rate of the melt material，is calculated. The experimental results show that during the production of amorphous strip，the reflux coming from surrounding gas and the internal molten pool will affect the temperature performance，and the average cooling rate of melt material is calculated to be 2.1×106 K/s，compared with the existing experimental conclusions，the reliability of the numerical simulation is verified.

Keywords：planar flow casting;molten pool;temperature field;velocity field;cooling rate

0  引  言

非晶帶材以其独特的机械、物理、化学和电磁特性，被广泛应用在各工业领域中。非晶带材的制取主要采取平面流铸技术（PFC），通过这项技术，可以制取厚度在20～60 μm之间，宽度达到100～350 mm范围的宽带^[1]。

在非晶带材制带过程中，喷嘴与铜辊表面之间形成的熔潭是影响制带的关键，国内外学者对熔潭形成机理以及稳定性进行了大量的理论分析和实验验证。Bussmann^[2]等建立了熔潭模型，通过有限体积法计算得到熔潭稳定后的流场及温度场分布，并改变上游自由表面夹角、熔体流量、辊体速度等参数，分析熔潭内部状态。Zhang和Atrens^[3]对平面流铸过程中的换热系数、成核温度以及晶核生长动力学规律等重要未知参数进行了计算和预测，并结合实验进行对比。Yu^[4]将系统换热以及晶体成核、生长相结合，验证了高过冷度对于晶体成核、晶核生长及宏观固液交界面温度、位置的影响，并得到晶粒的生长速度的关系表达式。

国内外学者的研究主要针对早期实验室设备的制带过程，对于已趋近成熟的工业制带工艺以及制带设备等的研究相对较少。本文针对熔潭形成建立相应的模型并进行相关的分析，得到熔潭外形及内部速度场、温度场随时间尺度的变化趋势，流体速度对于温度分布的影响，进而计算出非晶合金的凝固过程的冷却速率。

1  模型建立

1.1  数学模型

相较于整个制带设备的冷却系统，熔潭的外形尺寸非常小，并且涉及流体流动、自由表面形成、热量交换以及物相变化等，因此在分析过程中，需要依据实际情况约束，对模型进行一定的简化和假设：

（1）与非晶带材厚度相比，其宽度和长度可以近似为无限大，因此取熔潭的截面进行分析，简化为二维流动及换热分析。

（2）由于喷嘴铜辊间距的尺寸非常小，忽略流体扰动，熔潭内部的熔体以及外部的空气认为是不可压缩牛顿流体，并且其流动方式为层流。

（3）熔潭的外形尺寸相较于冷却铜辊直径很小，因此假设位于熔潭之下的铜辊表面为平面。

（4）熔体以10⁶K/s量级的冷却速度进行凝固，同时没有固定的凝固温度，忽略凝固过程潜热释放对温度场的影响，同时忽略成核温度同凝固点之间过冷度。

（5）所有材料的热物理性质均假定为常数，不随温度而改变。

基于以上假设，可近似得到熔潭的物理模型如图1所示。上自由边界及下自由边界主要影响熔潭的稳定性，固液交界线主要影响带材的厚度，熔潭形成的过程中，上、下自由边界及固液交界线的生长是主要检测的对象。

根据上述模型，建立以下控制方程：

其中κ为自由表面的曲率，σ为表面张力系数。

1.2  模型网格划分

根据模型参数，建立以下计算域以及进行相应的网格划分，并设置相应的边界。为使计算更加精确，在流体同固体的接触换热区域，建立比率为1.1的20层网格，如图2所示。

1.3  边界条件

根据划分的网格，设置如下的边界条件：

其中所有固体边界，均设置为无滑移条件。数值模拟需要的几何参数和热物理参数如表1所示。

1.4  数值模拟方法

根据以上的控制方程以及所设定的边界条件，设置瞬态的基于压力耦合求解器，同时设置流体体积函数的柯朗数（控制时间步长与空间步长的相符关系）为0.25。设置初始时间步长为10^-6s量级，待熔体接触到铜辊之后，调整量级为10^-8s，待熔潭达到稳定状态，带材可以连续生成，调整量级为10^-3s进行模拟。

2  结果与分析

2.1  速度场分布

通过计算得到的速度场随时间的分布如图3所示，由速度矢量图以及相对应的流场分布可以得到熔体以及周围空气的流动过程。图3中的黑线表示熔潭的边缘形状，即熔体同空气的交界线。图3（a）和图3（b）表示在t=0.06 ms，熔体从喷嘴流出但是并未接触到冷却铜辊表面时，熔潭内部的速度矢量垂直向下，而沿x方向的速度梯度为零。图3（c）和图3（d）表示在t=0.22 ms，熔体刚刚接触到铜辊表面时，此时，由于熔体的表面张力以及壁面滑移的作用，熔潭的外形尺寸有一定的扩大，熔潭底部的熔体受铜辊旋转产生向右的速度分量，同时在熔潭的左侧产生回流区域;熔体接触铜辊，上、下自由表面空气流动被截断，周围空气靠近上自由表面会形成更大的回流，而位于下自由表面的空气形成形状相近的流线。图3（e）和图3（f）表示t>0.42 ms，熔潭稳定后，可以明显地看到在熔潭内部形成了两处回流，同时外部的流场变化较小。

2.2  温度场分布

随着时间的变化，各阶段的温度云图如图4所示。在熔体流下的初始阶段，如图4（a）所示，熔潭内部温度保持为熔体流入温度，上自由边界附近温度变化比较明显，其主要原因是环境气体在该阶段形成的回流使热流发生紊乱，而下自由边界处的温度场则与熔潭外形保持近似并呈层状分布。当熔体初步接触到铜辊表面时，如图4（b）所示，高温熔体会与冷却铜辊迅速换热并快速冷却，上、下自由表面温度场变化较小，同时上自由表面外形基本形成，其附近温度场之后基本保持不变。熔潭稳定之后，如图4（c）所示，熔潭内部温度在靠近铜辊处形成层状等温线，下自由表面附近等温线同其形状近似相同，温度梯度方向向外。

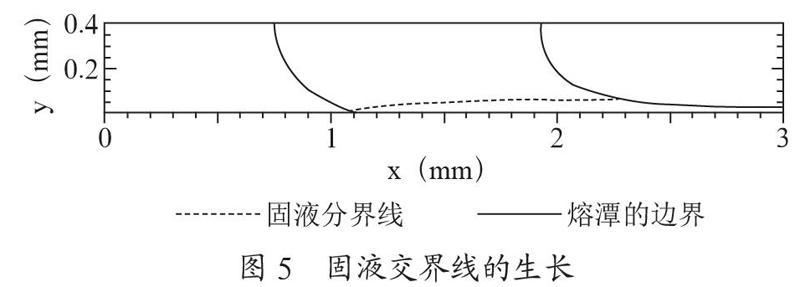
2.3  固液交界线

忽略过冷度对于熔体凝固成核的影响，同时由于合金没有固定的熔点，参考Wang^[5]的分析方法，假定T=1 373 K为熔潭内部固液分界线，如图5中点划线所示。同时根据图像，可以看出从熔潭中拉出得到的带材的厚度为0.03 mm，同生产设备得到的带材厚度接近。根据数值模拟得到固液分界线形成的时间约为0.23 ms，因此可以计算出熔体的凝固冷却速率为2.1×10⁶K/s，结合已有的结论，证明了该模拟的正确性。

3  结  论

通过对平面流铸过程中熔潭形成的数值模拟，得到了熔潭内部及周围环境温度场、速度场随时间的变化规律，并得到以下结论：

（1）熔体从喷嘴流出到形成熔潭这一过程所需时间为0.42 ms，并且熔潭达到稳定状态后，上、下自由表面形状和位置不再发生变化。

（2）在熔潭形成过程中，空气回流会在一定程度上影响到温度场的分布，固液交界面的生长可以反映带材的生成过程。

（3）熔体接触到铜辊表面快速凝固，其冷却速度约为2.1×10⁶K/s，与实际结果相吻合，验证了数值模拟的正确性。

参考文献：

[1] 宋言明，杨洋.非晶态薄带冷却铜辊用内反馈静压轴承数值模拟 [J].航空学报，2014，35（4）：1157-1164.

[2] BUSSNANN M，MOSTAGHIMI J，KIRK D W，et al. A Numerical Study of Steady Flow and Temperature Fields within A Melt Spinning Puddle [J].International Journal of Heat & Mass Transfer，2002，45（19）：3997-4010.

[3] ZHANG X，ATRENS A. Estimation of the Unknown Parameters in the Melt-spinning Process [J].Journal of Materials Science，1994，29（2）：544-547.

[4] YU H. A Fluid Mechanics Model of the Planar Flow Melt Spinning Process under Low Reynolds Number Conditions [J].Metallurgical & Materials Transactions B，1987，18（3）：557-563.

[5] WANG G X，MATTHYS E F. Mathematical simulation of melt flow，heat transfer and non-equilibrium solidification in planar flow casting [J].Modeling and Simulation in Materials Science and Engineering，2001，10（1）：35.

作者簡介：张斐然（1991—），男，汉族，河北衡水人，工程师，硕士，研究方向：船舶系统。

收稿日期：2021-04-06