基于DAG-SVMS 的非侵入式负荷识别方法*
2021-11-04徐元源李松浓
王 毅 ,徐元源 ,李松浓
(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.国网重庆市电力公司电力科学研究院,重庆 404100)
0 引言
智能电网建设是以提高生态可持续性、供电安全性和经济竞争力为目标[1],表现为提高负荷监测技术、提高终端用户响应速度、提高需求侧的节约能效、提供智能控制技术、分布式能源的自由接入[2]。非侵入式负荷识别作为非侵入式负荷监测的核心内容,在不改变用户电路结构的条件下,通过测量总负荷数据,即可获得系统内具体用电负荷的数量、类别、运行状态信息,安装和维护成本低,易于推广。该技术的实现,可为用户、电力公司以及设备提供参考[3]。用户端,用户用电信息得到反馈,提升节能意识,规范用电行为。电力公司端,能提高负荷预测的精确度,实现有效的负荷规划、电能调度。对设备制造商来说,可据此识别出故障或低效设备,加快技术革新,推动高能效设备研发。
目前,非侵入式负荷识别技术在国内外均有研究。文献[4]利用稳态功率信息建立隐马尔科夫模型优化分解方法,对低频混合功率分解得到单个设备运行状态,但识别率不高,不能识别负荷投切时刻。文献[5]利用动态时间归整(Dynamic Time Warping,DTW)算法计算实测电流稳态波形和样本库稳态波形的相似度来识别家用负荷,但无法识别变频设备和且小功率设备容易误识。文献[6]提取负荷稳态电流谐波并结合K-近邻(K-Nearest Neighbor,K-NN)算法进行负荷识别,为提高识别效果融入了核Fisher 判别方法,综合了K-NN 的简捷性和核Fisher 的非线性识别能力,但谐波信息易受外界环境影响,且小功率设备谐波易被大功率设备湮没。文献[7]中提取负荷暂态电流波形特征后,根据分类与回归树(Classification and Regression Trees,CART)算法训练决策树算法进行负荷识别,但决策树结果不稳定,类别太多错误率增加会加快。文献[8]以负荷开关时的独特暂态功率波形为特征,计算测试暂态功率波形与样本库波形贴近度实现负荷识别。另外,神经网络[9-10]也是常用的负荷识别方法,但该类方法需要大量的训练样本,训练参数多,可解释性差,使用受到限制。由于稳态类方法对软硬件要求相对较低,目前大多非侵入式负荷识别方法仍然是基于稳态的,但该类方法难以有效识别变频设备等持续变化负荷,同时,小功率设备容易被大功率设备湮没,易受外界环境干扰。此外,无论是稳态类还是暂态类方法,大多研究仅对特征差异明显的设备识别效果好,一旦特征发生重叠便难以有效识别。
综上,文中对不同负荷投切时产生的暂态电流波形并提取合适的特征量进行负荷识别,为避免设备特征重叠造成负荷无法辨识的问题,提出DAG-SVMS 负荷识别模型。为提高分类器识别准确率,采用PSO 算法优化分类器参数,同时,提出基于Gini 指数优化模型节点顺序的策略,以减少模型累积误差。最后,采用公开数据集BLUED 进行试验验证,结果表明提出的方法识别准确率高,识别速度快,具有可行性。
1 暂态电流特征提取
1.1 暂态事件检测
将电力系统由一个稳定运行状态过渡到另一个稳定状态的过程定义为暂态事件[11]。不同的用电负荷投入、切除以及运行状态发生改变时,都会伴随暂态事件的发生。文中使用相邻周期电流强度变化量来检测负荷暂态事件,定义第T 个周期的负荷的电流强度为:

式中,K 为一个周期内电流的采样点总数;i(k)为第T 个周期内第k 个采样点的电流值。
当电力系统内部各用电负荷稳定运行时,总线处相邻周期的电流强度差值趋近于0;若某一时刻相邻周期电流强度差值超过δ,则判定系统内负荷发生了暂态事件,记相邻周期中第二个周期电流起始时刻为暂态事件起始时刻。表示为:
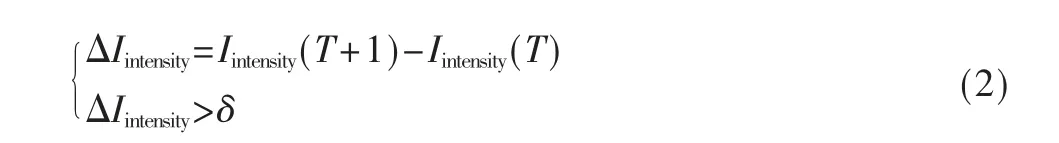
式中,ΔIintensity为第T 个周期与T+1 个周期电流强度的差值;δ 为暂态事件起始判定阈值。
检测到暂态事件的产生后,立即执行暂态事件结束算法,表示为:

式中,ε 为暂态过程结束的判定阈值;γ 为电流强度变化小于ε 的最小周期数;T 为电流强度变化小于ε 的周期数。
上式表达的具体含义为当ΔIintensity小于ε 的周期个数大于γ 时,则判定为负荷暂态事件结束。当前时刻减去γ 个电流信号周期后得到暂态事件结束时刻。可见,负荷暂态过程持续时间(暂态事件结束时刻与起始时刻的差值)为工频周期的整数倍。
1.2 暂态过程波形分离
检测到暂态事件发生后,电流有效值增大的过程为负荷投入,表现为负荷的开启或升档等操作,电流有效值减小的暂态过程为负荷的切除,表现为负荷关闭或降档等操作。检测到暂态事件后,执行如下:
(1)根据暂态发生前后电流强度的变化,判定系统暂态事件为投入还是切除。若判定为负荷投入,执行步骤(2)。若判定为负荷切除,执行步骤(3)。
(2)暂态事件电流波形与相同周期数量的暂态前的稳态电流波形作差,去除背景波形。
(3)暂态事件电流波形与相同周期数量的暂态后的稳态电流波形作差,去除背景波形。
示例见图1。
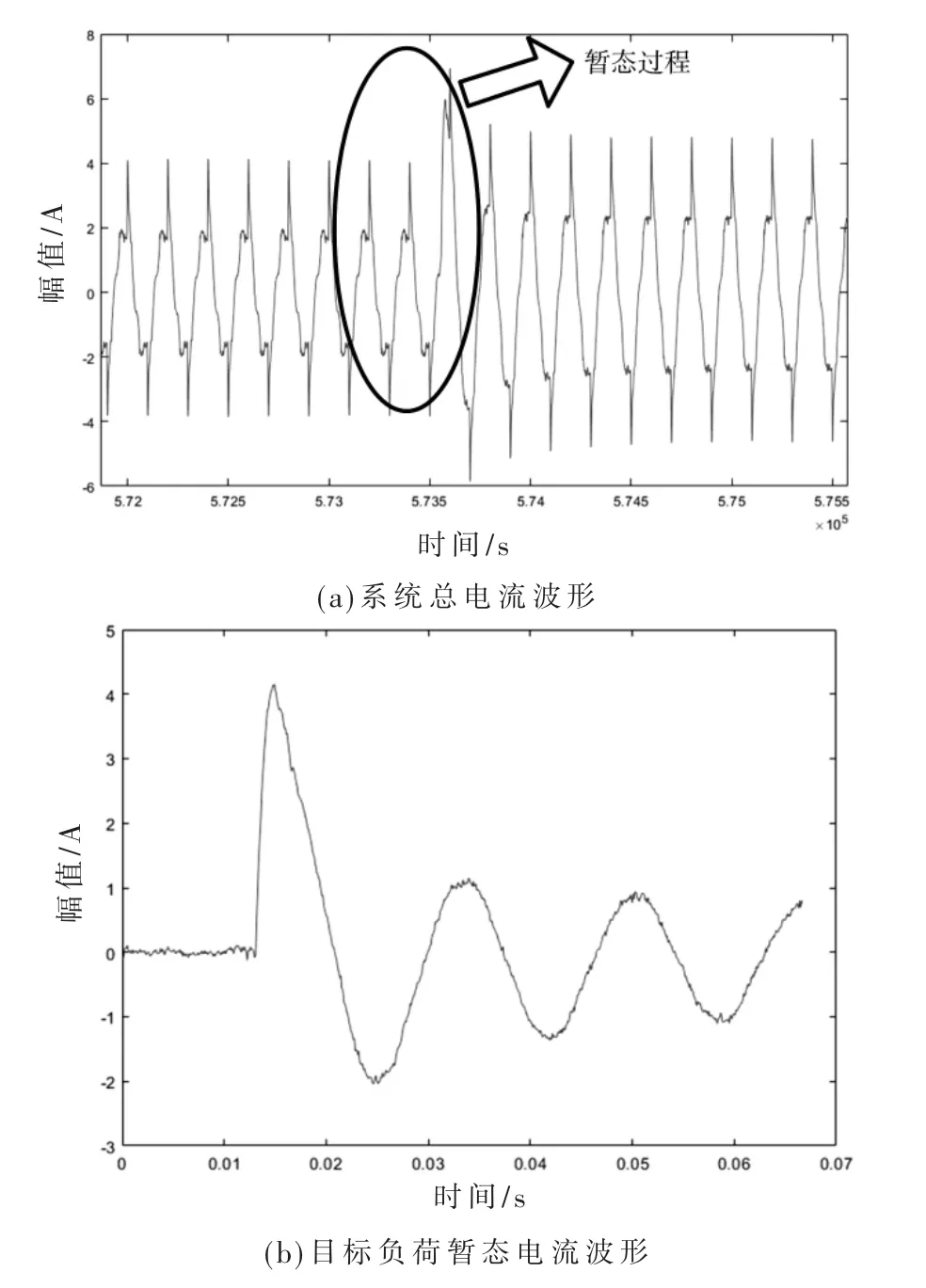
图1 暂态电流波形分离
1.3 暂态波形特征提取
为尽可能详细地反映各类暂态过程的特性,选择多种特征表征暂态过程。
(1)暂态过程持续时间T:暂态事件结束时刻与暂态事件起始时刻差值;
(2)暂态波形取绝对最大值Ip:暂态波形取绝对值后的最大值;
(3)峰峰值Ipp:暂态电流波形最大值与最小值之差;
(4)平均值Imean:暂态电流波形各采样点均值;
(6)电流强度Iintensity:将暂态电流波形按式(1)计算电流强度,采样点数为暂态事件电流采样点数;
(7)稳态波形有效值Irms:暂态事件前后稳态电流强度差值;
(8)峰均比Rpta:峰峰值与电流强度比值(Ipp/Iintensity);
(9)波形因数Fform:电流强度与绝对平均值比值(Iintensity/I′mean);
(10)波峰因数Fcrest:暂态波形取绝对最大值与电流强度比值(Ip/Iintensity);
(11)负荷标志位Iflag:根据暂态事件前后电流强度变化判断负荷投切,负荷投入时为1,负荷切除时为0。
对负荷暂态电流波形提取11 维特征,构建样本数据库。图1 特征提取如表1 所示。

表1 特征展示
获取到样本库后,对样本特征空间进行归一化处理,将负荷样本特征压缩至[0,1]之间,表示为:

式中,i∈[-1,N];j∈[1,11];N为样本个数;xij为第i个样本的第j 个特征值;xjmax为样本中第j 个特征对应的最大值;xjmin为样本中第j 个特征对应的最小值。
2 DAG-SVMS 负荷识别模型
非侵入式负荷识别可依据的特征多,但在实际应用中能够获取的样本较少,是典型的小样本高维数据问题,且需要快速识别。SVM 是一种建立在统计学基础之上的分类器,在小样本、非线性以及高维数据的模式识别中表现出十分突出的特性。传统的SVM 是解决二分类问题的,但实际中大多是多分类问题,因此,需要将二分类扩展至多分类[12]。
2.1 SVM 基本原理
假设样本集合:
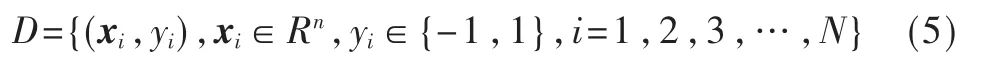
式中,xi为样本数据;yi为xi类标签;N 为样本 个数;n 为样本维数。
SVM 基本思想是构造最优超平面将不同类别的样本分开,超平面构造原则为距离该平面最近的样本到该平面的间隔最大。得到优化问题如下:
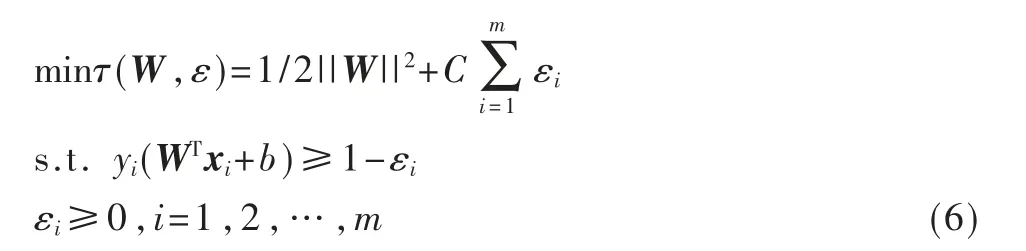
式中,W 为超平面法向量;b 为超平面的偏移量;C 为惩罚参数;εi为松弛变量。
构建拉格朗日函数:
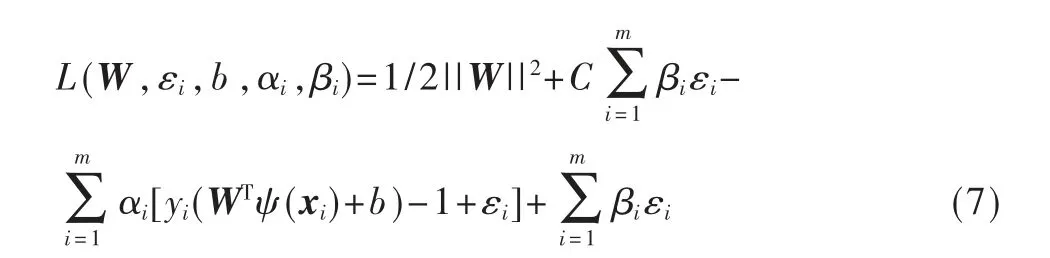
式中,αi和βi为拉格朗日乘子。
对W、b 和εi求偏导为0,代入式(7),得:
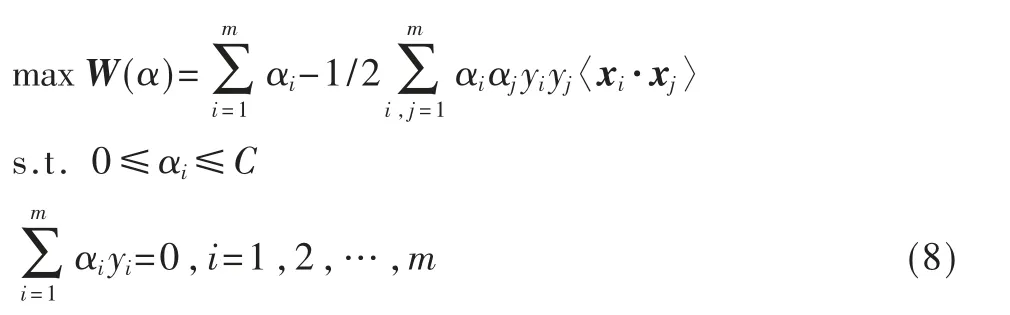
求解式(8)得到分类决策面:
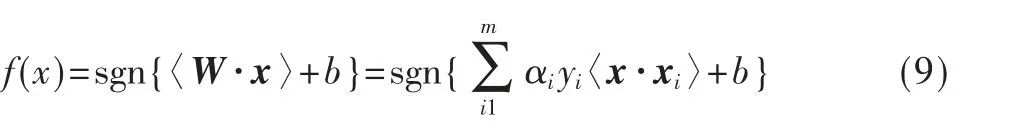
称αi>0 对应的样本为支持向量。
数据样本在低维空间不可分时,可通过核函数映射到高维空间ψ:x→ψ(x),在高维空间中求解最优线性分类超平面,将高维空间求解的线性分类超平面转为低维分类超曲面。SVM 通过核函数巧妙地避免了由低维映射至高维带来的维数灾难问题,解决了样本的非线性可分问题。根据Mercer 定理,核函数要求满足:

大量文献与试验结果表明,高斯核函数在模式识别问题中表现出优越性能,因此,选择高斯径向基核函数。
2.2 SVM 参数优化
2.2.1 SVM 参数影响分析
SVM 分类性能主要受误差惩罚参数C、核函数及其参数的影响[13]。文中SVM 性能主要受误差惩罚参数C和高斯径向基核核参数g 影响。C 越大表示越不能容忍误差,分类器更加契合训练样本集,易过拟合,泛化性低。C 偏小易出现欠拟合,训练误差大,对新样本分类变差。g 决定数据映射到高维空间的新分布,g 过大则支持向量过于紧密,支持向量少,分类器难以获得优质分类性能,g 过小则支持向量关系过于松弛,支持向量多,难以保证分类器泛化性能。支持向量的数量决定了分类器复杂度。
2.2.2 SVM 参数优化
PSO 算法是依据鸟群觅食行为所研究的群体协作优化算法[14]。首先,随机初始化M 个粒子,然后,通过迭代的方式获得最优解,每次迭代粒子通过跟随个体极值pid和全局极值pgd更新速度,根据速度进一步更新粒子下一次位置位置,并进行适应度评价,以此迭代循环,直至找到最优解。粒子速度与位置更新公式如下:
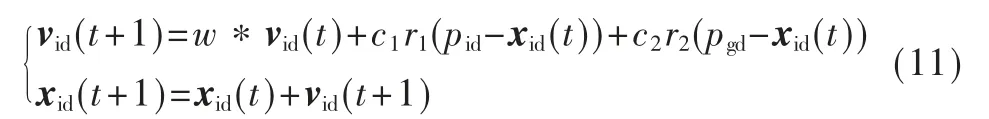
式中,vid为粒子的速度;xid为粒子的位置;w 为惯性权重;c1、c2为学习因子;r1、r2为均匀分布在[0,1范围内的随机数。
SVM 参数优化框图见图2。
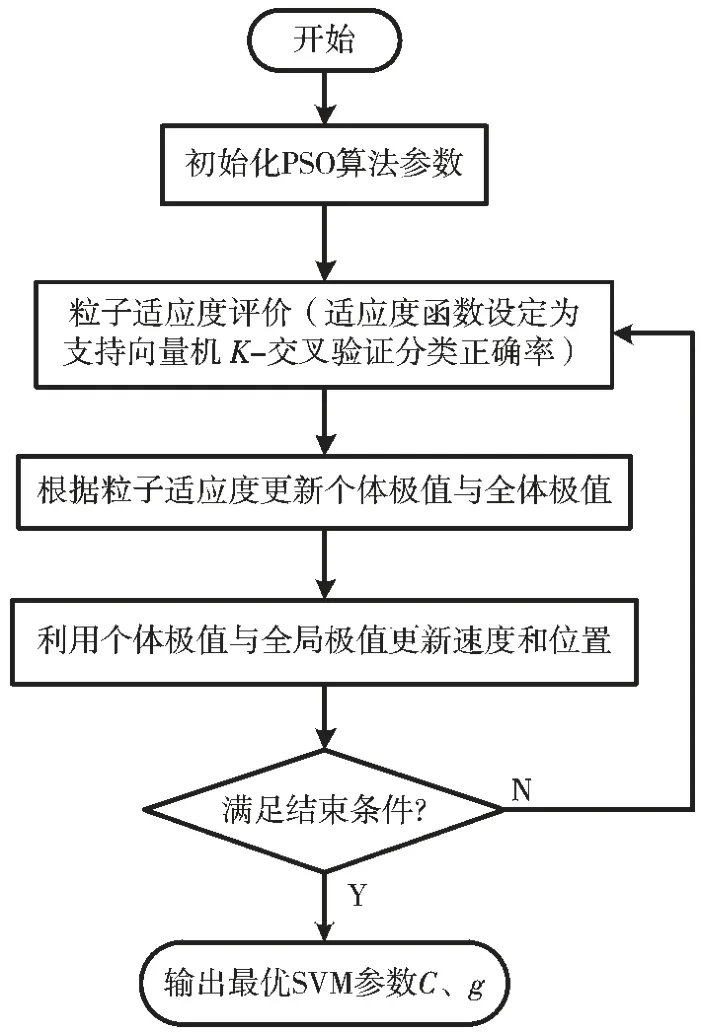
图2 PSO 算法优化SVM 参数
2.3 DAG-SVMS 算法
假设一个含有N 个类别的数据集合,将其中任意两类样本构建一个分类器得到个分类器,将这些分类器搭建为DAG 图,将得到N(N-1)/2 分支节点和N 个叶节点。DAG-SVMS 采用“排除”的思想,样本将随着根节点从上到下流动直至叶节点,分支节点决定样本具体被分类到左分支还是右分支,最终叶节点的类别就是该样本所属类别,完成一次分类需N-1 个节点。示例见图3。
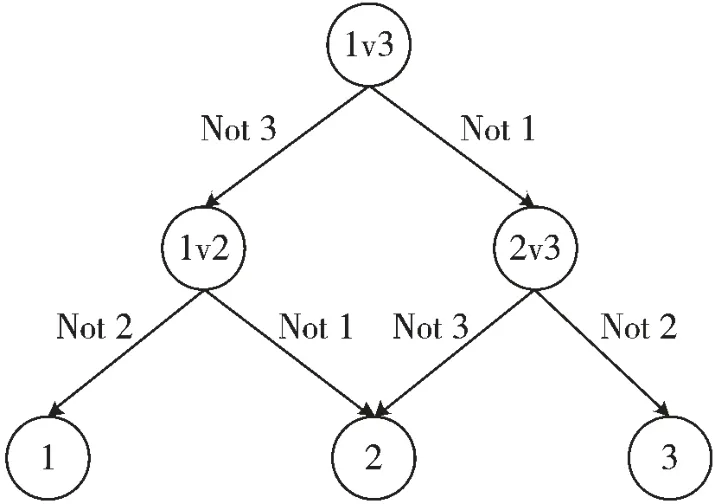
图3 三分类DAG-SVMS 算法
相对于常用的1-V-1 SVM 多分类算法,DAGSVMS 识别速度更快;相对于1-V-R SVMS 多分类算法,DAG-SVMS 训练时间短。同时DAG-SVMS 不存在误分、拒分区域,分类精度也有所提高。由于DAG-SVM 采取层次结构,误差累计是层次结构不可避免的弊端,即高层节点对整体样本的分类准确率影响更大。鉴于此,文中首先根据负荷标志位,将样本数据分为负荷的投入和切除两部分,分别训练DAG-SVMS 模型,以减少DAGSVMS 层数,当系统采集到样本后根据标志位判断样本属于投入还是切除,然后将样本数据送入对应DAGSVMS 进行识别。下面提出基于Gini 指数的节点顺序优化策略。
2.4 Gini 指数
Gini 指数用于度量样本数据的不纯度和不确定性,表示为:

式中,pi为D 中样本属于第i 类的概率;D 表示样本数据集。
假设样本集被节点划分为两个子集合D1、D2,则经过该划分后样本的Gini 指数降低为:

经过该划分,产生的Gini 指数差为:
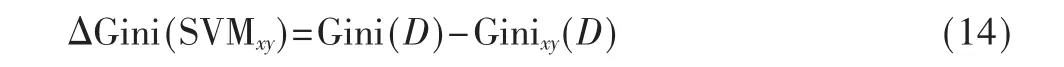
由于Gini 指数越小样本越有序,将划分后的样本Gini指数最小化,即保证划分前后数据的Gini 指数差值最大,使划分结果更加有序。文中对节点顺序的优化为:首先使用各个分类器对样本训练集进行划分,选择Gini 指数差值最大的节点作为根节点,然后将划分后的样本集D1、D2分别视为独立集,在下一层中选择Gini 指数差值最大的分类器作为当前节点,以此类推,搭建DAG-SVMS 结构。
2.5 算法框图
文中算法框图如图4 所示,包括:数据采集、事件监测、特征提取、负荷辨识,分为辨识模型训练阶段和在线识别两个阶段。考虑到实际用户家庭负荷用电习惯,暂态事件过程持续时间极短,文中假设各负荷独立,不存在多种负荷同时投切这一特殊情况。
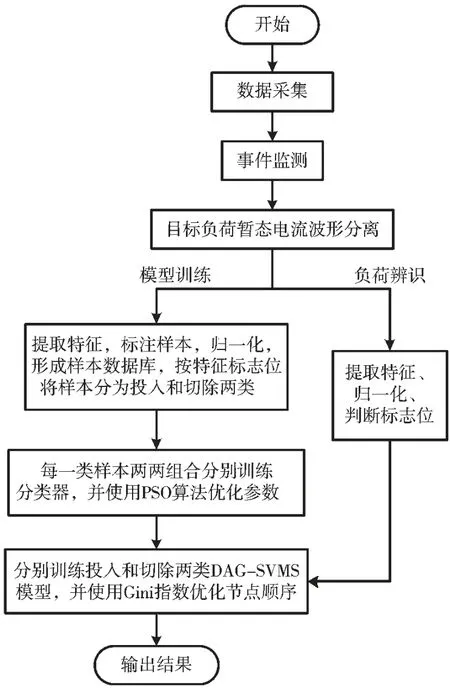
图4 算法流程
3 实验验证
采用BLUED[15]数据集进行仿真验证分析,数据来源于某家庭电力总线端口处,共采集了8 天,采样频率为12 kHz,包括电压、电流数据,并配备各用电设备的暂态事件投切时刻表。软件平台使用MATLAB2018a,辅助工具箱Libsvm3.24,硬件平台使用Intel Core i5-4210U 2.40 GHz,4GB RAM电脑。从数据集中选取5种投切次数较多的用电设备用于实验验证,暂态事件起始判定阈值设定为功率最小负荷浴室顶灯电流强度的1/2,暂态过程结束的判定阈值设定为浴室顶灯电流强度1/5,提取11 维特征向量形成样本数据空间。共5 种用电设备的投切,10 类暂态过程,详见表2。
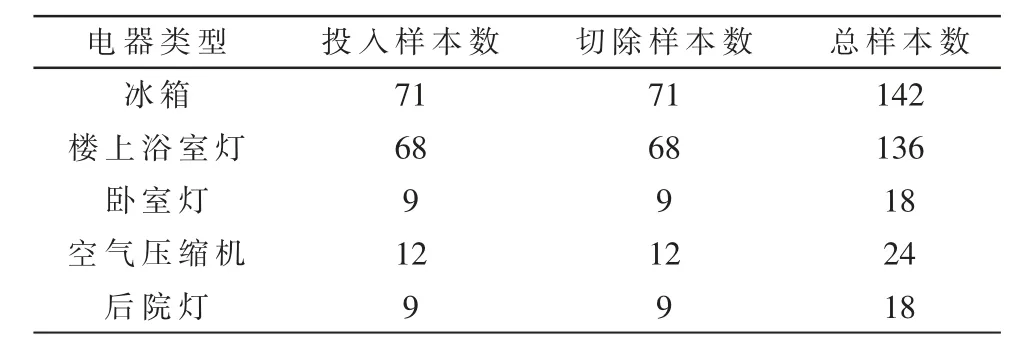
表2 样本数据组成
分别从10 类暂态过程中随机选择60%的数据样本用于训练,剩余40%样本用于测试,执行10 次。评价指标选用准确率:

PSO 算法最大迭代次数设置为100,搜索空间维数d=2,初始化个体数目N=30,学习因子c1=2、c2=2,惯性权重w=0.65,粒子位置值范围[-10,10],折叠交叉数K=5,实验结果如表3 所示。
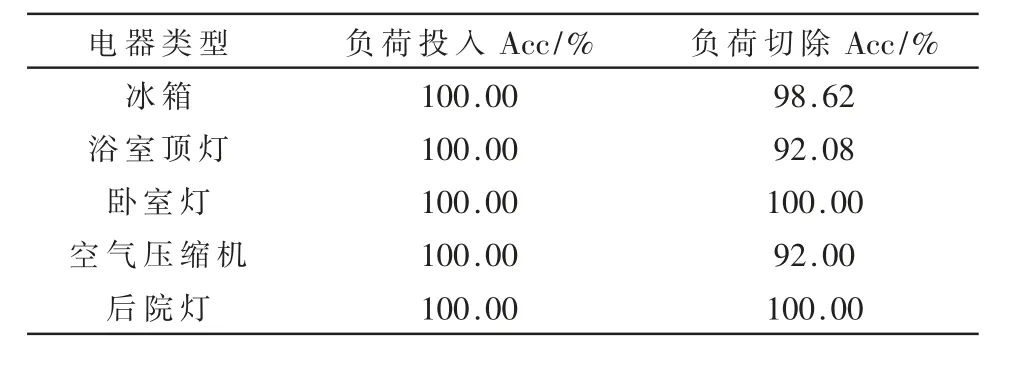
表3 负荷识别正确率
从表3 可以看出,文中方法对各负荷投入识别率均为100%,负荷切除识别率相对偏低,这是因为负荷切除时的暂态过程持续时间偏短,外加电力线中噪声干扰,导致暂态特征区分度减弱。算法平均识别率为97.69%。
分别使用1-V-1 SVMS、1-V-R SVMS、传统DAGSVMS 以及文中优化改进的DAG-SVMS 算法进行识别性能对比分析。分类器参数优化前,使用平台默认参数结果如图5 所示。从图5 中可以看到,PSO 算法优化后,各多分类SVM 算法识别准确率均大大提高,文中DAGSVMS 优化前后识别准确率均优于传统SVMS,且波动较小,识别结果稳定。
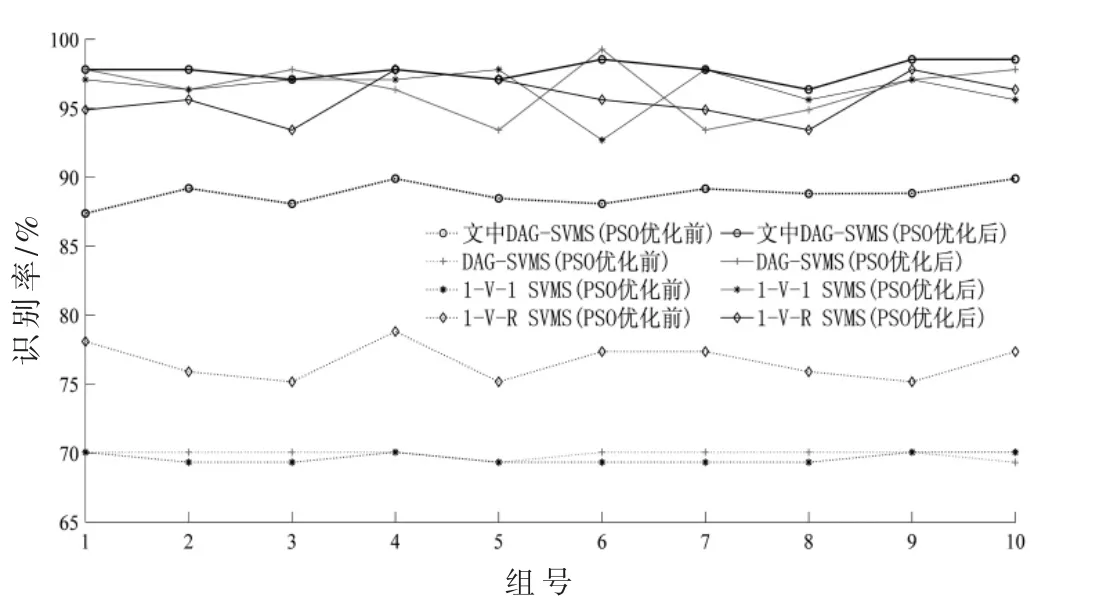
图5 多分类SVM 算法测试结果
多分类SVM 算法训练、测试结果如表4 所示,表4中,各项指标由10 次实验结果平均得到。可以看到,文中算法平均训练时间最短,为20.35 s,单样本平均识别时间最快,为1.53 μs,平均识别率最高,为97.69%,均为最优。由于文中算法在训练模型前,根据负荷标志位对模型进行了简化处理,模型结构简单,训练时间减少。同时,分类识别时所需分类器判决次数少,识别时间更快。
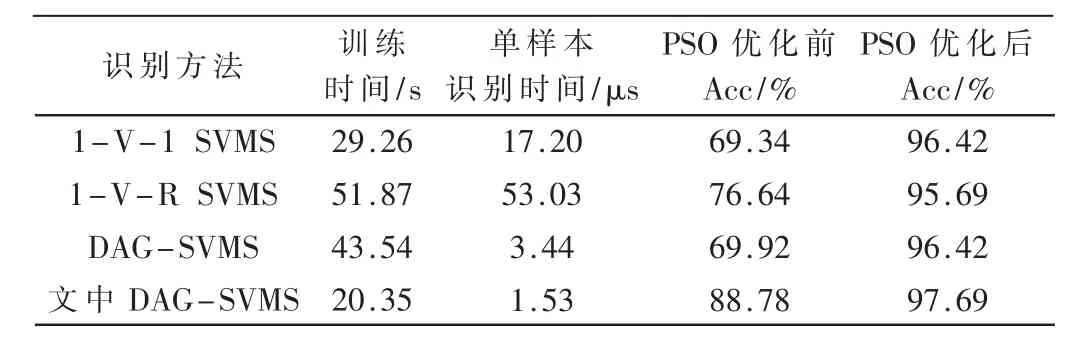
表4 多分类SVM 算法训练、测试结果
使用目前负荷识别领域常用的BP 神经网络、K-NN算法、CART 算法与文中优化改进DAG-SVMS 算法进行性能对比结果如图6 所示。
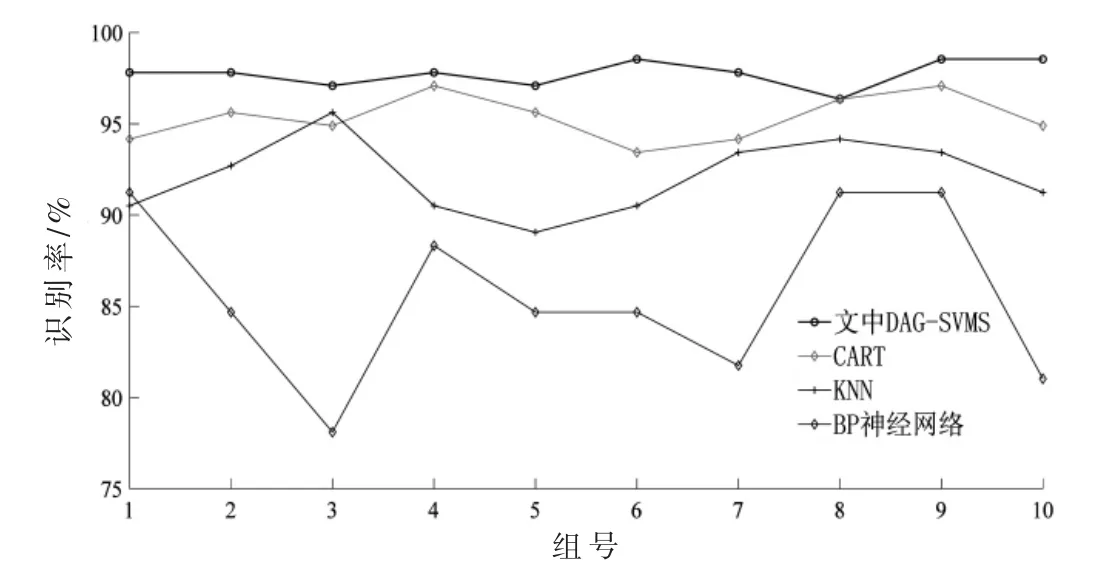
图6 不同算法的识别结果
从图6 中可以看出,文中DAG-SVMS 算法10 次实验结果识别准确率均高于其他几种常用算法,均保持在95%以上。进一步整理实验结果,如表5 所示。
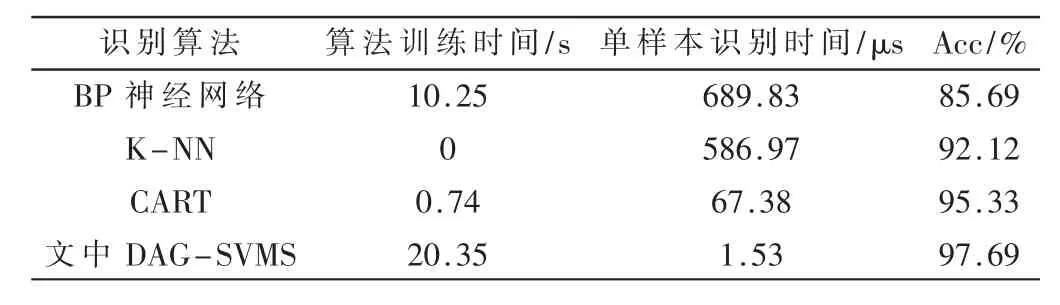
表5 不同算法实验结果
其中,K-NN 算法K 值为样本识别准确率最高情况下的对应值,该算法直接计算样本类别,因此,无训练时间。可以看到,文中方法单样本识别时间仍为最短,仅为BP 神经网络的0.22%、K-NN 算法的0.26%、CART 算法的2.27%。识别准确率上,平均识别率均高于其他几种算法。从训练时间角度看,文中算法平均离线训练时间最长,为20.35 s,但实际应用中,考虑到系统通信模块、人机交互等,文中算法负荷在线识别速度快,识别准确率高,故适合在线识别。
最后,从表6 中可以看出,文中DAG-SVMS 算法在节点顺序优化后,平均识别准确率提高1.04%百分点,反映了节点顺序优化方法的有效性。

表6 节点顺序优化前后对比
4 结论
针对稳态类方法识别负荷的不足,文中以暂态电流为特征,提出了一种基于改进DAG-SVMS 的非侵入式负荷识别方法。包括事件检测、暂态波形分离、特征提取,为解决特征类似负荷的识别问题,以SVM 为分类器,搭建DAG-SVMS 负荷识别模型,同时,优化模型中的分类器参数和节点顺序,以进一步提高识别准确率。实验结果表明文中算法识别准确率高,识别速度最快,实用性强,适合在线识别。
