基于非正交波形的超奈奎斯特采样*
2021-11-04马冰,白勇
马 冰 ,白 勇
(1.海南政法职业学院,海南 海口 571100;2.海南大学 信息与通信工程学院,海南 海口 570228)
0 引言
频谱资源紧张是目前的无线和有线通信技术面临的主要挑战之一。特别是在未来6G 传输系统,用户需求和移动终端的不断增长,人们对频谱效率的要求越来越高。在未来万物互联的时代,亟需新的物理层技术来提高频谱效率。超奈奎斯特(Faster-Than-Nyquist,FTN)传输通过压缩相邻脉冲之间的发送间隔来提高频谱效率。FTN传输技术是Mazo 则在1975 年首次提出的[1-2]。Liveris 等第二次发现FTN[3]并提出了较为实用的FTN 方案,利用升余弦脉冲替代sinc 脉冲[2]。Rusek 等将Mazo 限从时域的FTN 推广到时频二维的FTN,提出了多载波的FTN[4-5]。FTN 在过去的几十年内得到了快速的发展,已成为提高频谱效率的重要技术,广泛应用于5G 蜂窝微波无线回程[6]、beyond 5G 无线通信[7]、可见光通信[8]、光纤通信和卫星通信。但是,升余弦等传统的正交波形的时频聚集特性较差,拖尾衰减慢,导致接收端的最大后验概率(Maximum A Posteriori,MAP)均衡复杂度一般也较高,这导致正交波形不能很好适应FTN 传输。因此,本文研究了基于非正交波形的FTN 新技术。
在FTN 系统中,波形条件可以放宽,选择适合FTN传输的新波形。现在关于FTN 的研究大都是基于复数域正交的成形脉冲,例如sinc 脉冲、升余弦脉冲。复数域非正交脉冲波形的能量聚集特性好,拖尾衰减快,接收端的均衡复杂度一般较低,比较适合FTN 传输。常见的复数域非正交的脉冲有:扩展高斯脉冲(Extended Gaussian Functions,EGF)脉冲[9-10]、全向正交变换算法(Isotropic Orthogonal Transform Algorithm,IOTA)脉冲、高斯脉冲等。IOTA 脉冲是EG 脉冲的特例。在FTN 均衡方面,本文采用Ungerboeck 模型[11-12]替换了传统的Forney 模型[13]。
本文的主要贡献是用非正交的新波形替换传统FTN中的正交波形,研究了基于非正交波形的FTN 编码调制新技术。对于单载波FTN,由于非正交波形具有良好的时域聚集特性,因此其对应的FTN 均衡在保证误码性能的前提下能够大幅度降低复杂度。
1 超奈奎斯特系统模型
1.1 发送端模型
单载波FTN 发送端模型如图1 所示。信源un经过信道编码、交织、星座映射得到星座点符号an。an经过FTN 调制得到发送信号sa(t),即:

图1 超奈奎斯特发送端模型
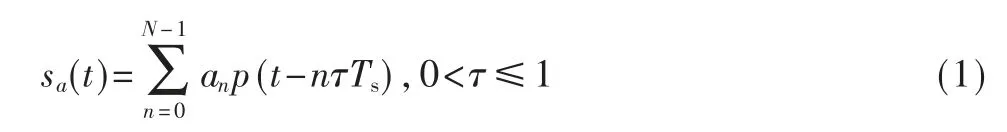
其中,τ 表示FTN 系统的压缩因子,Ts表示Nyquist 符号周期,p(t)表示成形脉冲,N表示符号个数。τ改变了 相邻成形脉冲之间的发送间隔即改变了符号周期。当τ<1时,在相同时间段内发射机可以发送更多的成形脉冲。
发送信号sa(t)对应的功率谱密度(Power Spectral Density,PSD)[14]为:

1.2 接收端模型
接收信号r(t)=sa(t)+n(t),其中n(t)表示白噪声过程。接收信号在t=kτTs时刻进行采样,则接收信号的第k 个采样值为:

最优性能的接收机即如图2 所示的Turbo 迭代接收机。由于系数{pl}具有对称特性,摈弃传统的Forney 模型[13]对应的MAP 算法,采用Ungerboeck 模型[11-12]对应的MAP 算法,其转移概率为:

图2 超奈奎斯特的均衡示意图

2 成形脉冲
在FTN 系统设计中,将成形脉冲因素考虑进来。
2.1 复数域非正交成形脉冲
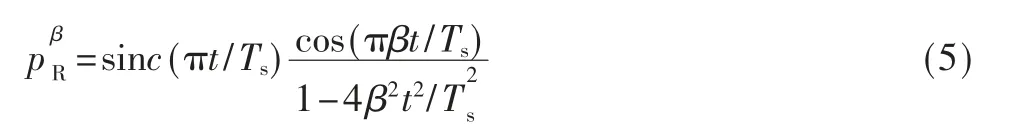
其中,β表示滚降因子。图3 中“Rcos”代 表升余弦成形脉冲的波形。

图3 升余弦、高斯、EGF 的时域波形对比

其中,σ 表征 能量分 布因子,σ>0。EGF 成形脉 冲[13-14]pE(t)为:


2.2 功率带宽与干扰强度
当对成形脉冲进行±ζTs的截断时,脉冲时域的截断必然导致脉冲的频谱展宽。本文用功率带宽替代传统的绝对带宽。国际电信联盟在ITU-R SM.1541-3 中定义了99.5%功率带宽。为留出更多的余量,本文采用99.99%功率带宽。在后续的分析中ζ=3,Ts=1。高斯脉冲(σ=0.56)、EGF 脉冲(σ=0.56,υ0=0.707)、升余弦脉冲(β=0.3)具有近似相等的99.99%功率带宽W 如表1 所示,表中“×2”表示双边带。定义干噪比[15](Interference-to-Noise Rate,INR):


表1 成形脉冲的99.99%功率带宽
定义干扰强度因子[15]:

当γ>1,FTN 经历强干扰。FTN 系统经历的干扰随着τ 的减小而增大。当τ≤0.46 时,3 种成形脉冲对应的FTN 系统都将经历强干扰。
3 仿真结果分析
式(4)中的MAP 均衡的复杂度为O(ML)。为了提升频谱效率,需要减小τ,对应的L 也将增大。L 较大导致MAP均衡复杂度太高。在复杂度和误码性能都在可接受的范围内,FTN 均衡实际采用L′个抽头,均衡复杂度为O(ML′),且L′≤L。
3.1 相同波形的超奈奎斯特性能比较
仿真参数如下:τ=0.6,1/2 码率的(7,5)8卷积码,调制阶数为4。两种成形脉冲在不同抽头个数对应的误码性能如图4、图5 所示。在图中,C4 表示L′=4,其他标识类推;ID1 和ID5 表示迭代次数分别为1 和5。

图5 实际抽头个数L′对均衡的性能的影响(EGF)
在图4 中,对于升余弦脉冲,当迭代次数为5 时,L′=6 和L′=3 对应的误码性能相差1 dB;L′=6 和L′=4 的误码性能相差0.3dB。L′=4 的MAP均衡,在大幅度降低复杂度的同时,误码性能损失很小。当不进行迭代时,降低抽头个数对误码性能影响较大,最大有4 dB 差异。

图4 实际抽头个数L′对均衡的性能的影响(升余弦)
在图5 中,对 于EGF脉冲,5 次迭代,L′=2 和L′=4对应的误码性能相当。不迭代时,误码性能为10-5时,L′=2 和L′=4 对应的信噪比相差大约0.8 dB。
抽头数L′在保证误码性能同时大幅度降低均衡复杂度。减小抽头个数,则式(3)变为:

其中,M 其中,Ps表示发送信号的功率。根据上述分析可以看出,忽略抽头就是将干扰视作噪声。这将导致信噪比降低,降低的百分比为: 可以看出,当抽头pl数值较小和信噪比较高时,抽头降低的信噪比可以忽略不计。 对于同一种成形脉冲,以高斯脉冲为例,随着τ 减小,干扰将逐渐增大,干扰从弱干扰过度到强干扰。如图6 所示,τ=0.4 时,系统经历强干扰。误比特性能为10-5时,与较弱干扰时(τ=0.5~0.9)FTN 系统的误码性能相比,强干扰的FTN 系统的误码性能有4.5 dB 的损失。当系统经历强干扰时,需要寻找更强的信道编码增强系统的抗干扰性能。 图6 基于高斯脉冲的系统误码性能 选择99.99%功率带宽近似相等的波形,如表1 所示。基于3 种成形脉冲的FTN 编码调制性能如图7 所示,其对应的星座映射为4QAM。在高信噪比下,EGF、高斯成形脉冲相比于升余弦成形脉冲能够带来显著的性能增益。当干扰为非强干扰时,以τ=0.6 为例,当误码率为10-5时,EGF、高斯成形脉冲相比于升余弦成型分别有1.9 dB 和1.6 dB 的性能增益。而此时基于EGF、高斯成形脉冲的均衡复杂度(O(42))是基于升余弦脉冲均衡复杂度(O(44))的1/16。当干扰为强干扰时,以τ=0.4 为例,当误码率为10-5时,EGF、高斯成形脉冲相比于升余弦成形分别有4 dB 和3.5 dB 性能增益。而此时基于EGF、高斯成形脉冲的均衡复杂度(O(5×43))是基于升余弦脉冲均衡复杂度(O(20×45))的1/64。可见,选择合适的非正交成形脉冲,不仅能够显著减少干扰对系统误码性能的影响,而且能够明显降低译码复杂度。τ 从0.6 减小至0.4 时,FTN 系统的干扰因子γ 从0.58 增大至1.4,此时非正交成形脉冲相比于正交脉冲之间的信噪比增益越大。 图7 3 种波形下的FTN 性能(τ=0.6,0.4) 本文研究了基于非正交的高斯和扩展高斯(EGF)脉冲成形的FTN 编码调制新技术,并与传统的正交波形FTN 进行了对比分析。当τ=0.4 时,在误码率为10-5条件下,基于EGF 和高斯成形脉冲的新技术相比于传统升余弦的FTN 技术分别有4 dB 和3.5 dB 的成形增益。由于非正交波形具有良好的时域聚集特性,时域抽头数少,新技术的MAP 均衡复杂度大大减少,可比升余弦FTN 有一个数量级意义上的降低。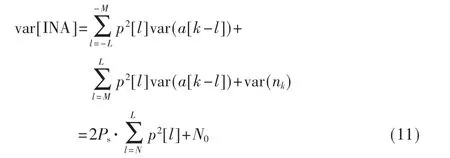


3.2 不同波形的超奈奎斯特性能比较

4 结论
