基于改进模糊控制的无刷直流电机控制系统

刘 甫，曾国辉，黄 勃，刘 瑾，韦 钰

（上海工程技术大学 电子电气工程学院，上海 201600）

0 引言

无刷直流电动机（BLDCM）具有响应速度快、功率因数高、运行平稳、体积小、可靠性好、效率高、维护成本低等优点，因此得到了广泛的应用[1]。由于常规控制中电机的绕组电流和转矩之间存在非线性耦合，因此很难对电机进行精确控制。高性能驱动系统最重要的特点是快速、精确的响应，快速从负载扰动中恢复速度。针对电机驱动系统的控制问题，已有许多改进方法，如模型参考自适应控制器、滑模控制器、变结构控制等控制器，这些控制器的设计依赖于精确的数学参数[2]。在众多的控制器中，模糊控制器是比较简单的一种，在响应速度快、对参数不敏感等方面优于其他智能控制器。另一方面，模糊逻辑等智能控制器的设计不需要被控对象精确的数学模型[3]。这种智能控制器的主要特点是简单，数学设计要求不高，适用于处理电机的非线性和不确定性问题。

本文在转速外环中采用模糊PID双模控制器，并在模糊PID基础上进行了改进，提出了变论域的模糊PID双模控制策略，并通过实验验证。

1 BLDCM的数学建模

在建立数学模型之前，我们做出如下假设：

1）定子绕组是三相对称且完全分布的；

2）磁路是不饱和的；

3）忽略涡流损耗和磁滞损耗；

4）气隙磁场是方波；

5）忽略电枢反应和换相过程的影响。

在这些条件下，Y接无刷直流电动机的数学模型可以表达如下。三相定子电压方程：

其中，ua、ub、uc为定子三相绕组端电压，Ra、Rb、Rc为定子三相绕组电阻，ia、ib、ic为定子三相绕组电流，Lbb、Laa、Lcc为定子三相绕组自感。Lab、Lba为A相绕组和B相绕组间的互感，Lac、Lca为B相绕组和C相绕组间的互感，Lbc、Lcb为B相绕组和C相绕组间的互感，ea、eb、ec为定子三相绕组上的反电动，ua是中性点电压，p是微分算子。根据上面的假设，可以令:

这样可以将式(1)化为:

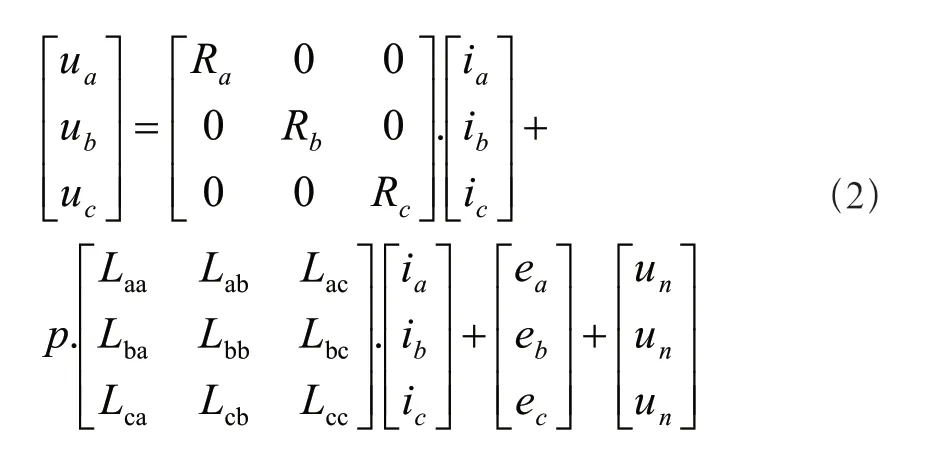
因为三相绕组呈星形连接，则有:

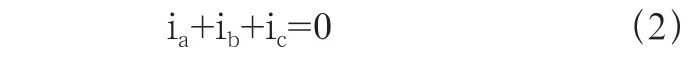
将该式代入式(2)中，可以得：

无刷直流电动机的电磁转矩和机械运动方程分别为式(4)和式(5)。

根据电压方程得电动机的等效电路图如图1所示。

图1 直流无刷电机的等效结构

2 双模控制器设计

传统的PID控制器在各种工程应用中得到了广泛的应用，但对复杂多变的环境适应能力不强，同时PID控制参数在整个控制过程中一旦确定，一般都是固定不变的。而模糊控制不但不依赖被控对象的数学模型，而且具有良好的鲁棒性和控制性能。但是，单纯的模糊控制器也有其缺点。例如，模糊规则和隶属度函数依赖于经验，不合适的模糊处理会导致系统的控制精度和动态品质下降，同时模糊逻辑控制系统由于没有积分作用，也可能产生稳态误差[4]。

针对上述问题，本文提出在速度外环设计了模糊控制与PID调节相结合的双模控制器。控制器模型如图2所示。控制器以速度误差与设定阈值之间的关系作为比较依据，当速度与实际速度误差大于设定值时，此时速度误差较大，选用模糊控制。当速度误差小于设定值时采用传统PID控制，此时转速已基本趋于稳定，故选用PID控制。同时，在模糊控制器的设计中引入变论域（Variable Universe）的思想，实现控制性能的提高。

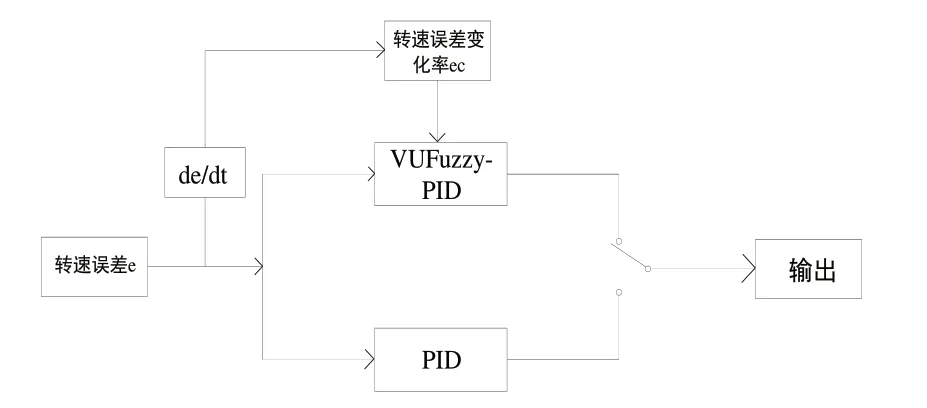
图2 模糊PID双模控制器结构图

2.1 双模控制器基本原理

如图3所示，电机的给定转速、实际转速的误差e与误差的变化率e作为模糊控制器的输入变量。输出变量为PID的3个参数的校正量Δkp，Δki，Δkd。

图3 模糊PID控制结构

本系统中将模糊控制器的输入输出论域设为［-6，6］，并离散化，分别为{NB，NM，NS，ZO，PS，PM，PB}，建立“三角形”的隶属度函数。根据PID不同参数调整模糊的规则，得到得到输出变量Δkp，Δki，Δkd规则表，如表1所示。

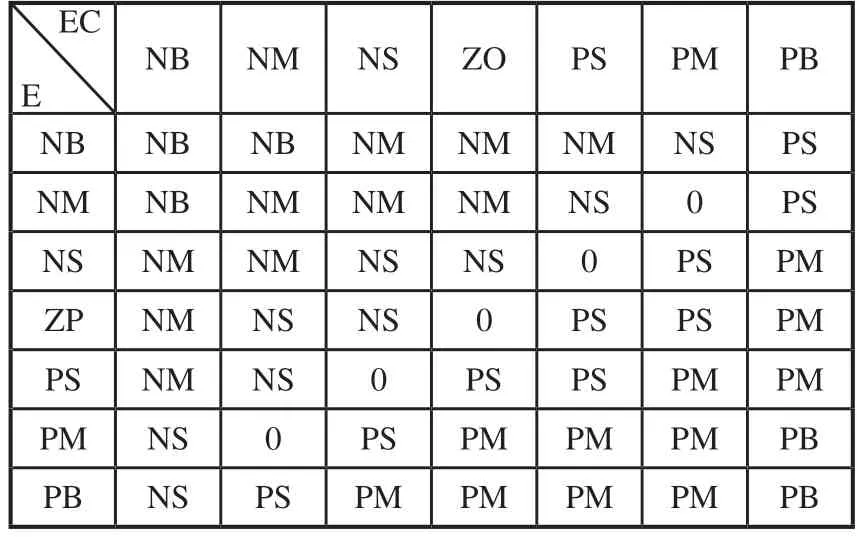
表1 模糊控制规则

将速度误差和速度误差变化率设为ke和kec，输出比例因子设为ku，这三个参数的选择对机控制系统的性能有很大的影响。

当保持kec不变，ke增大时，系统响应速度变快；当ke过大时，系统超调变大，过渡时间变长；当kec不变，越大，系统超调减小，稳态时间变长；选择的比例因子ku越大，系统响应越快，但如果它太大，则系统会产生振荡，当它太小时，稳态时u间就会ke变长。

综上所述，量化因子和比例因子通常会影响模糊控制的效果，模糊逻辑控制与传统的PID控制一样存在着动静态性能的矛盾，因为本文提出的模糊PID双模控制具有PID控制环节，因此可以提高系统的稳态性能，参数的选择应着眼于提高系统的响应速度和减小超调量。通过以上分析和反复模拟研究，获得最佳的量化因子和比例因子数据。

2.2 去模糊化

本文采用“重心法”对模糊推理得到的模糊集合去模糊化，使用本方法可使输出更平滑。公式如下所示：

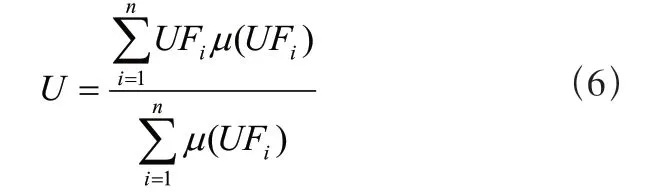
式中：μFUi为第一个i条规则的隶属度；FUi是第一个i规则的输出中心点。

2.3 变论域模糊控制器的设计

在完成模糊PID控制器设计时，量化因子和比例因子不能再次改变，导致自适应能力大大削弱。因此，模糊控制器可以通过收缩扩展因子使论域可变，实现控制性能的提高[7]。基本的模糊控制器论域如图4所示。

图4 基本论域

显而易见，当控制过程中误差变小时，[-E，E]域太大。如果系统继续使用该领域进行模糊推理，必然会导致控制精度的降低。由此，具有可变伸缩因子的模糊控制器如图5所示。

图5 变论域图示

定义α：X→[0,1]，x|→α(x)作为论域X的伸缩因子，满足下列条件：

对偶性：（(∀x∈X）α（x）=α（-x）；

空属性：α（0）=0；

单调性：α在论域[0,E]严格单调递增；

协调性：（(∀x∈X）（｜x｜≤α（x）E）;

上述条件应作为变伸缩因子的选择和构造原则，因此，输入论域伸缩因子的一种常用形式是：

e,e可以看作x，分别是输入误差和误差变化率的精确值。可以看出，系数k和λ越小，伸缩系数越大。在这种情况下，系数变化大，则伸缩效应越明显，反应越快[8]。但在实际系统中，应考虑综合指标。一些智能优化算法如遗传算法在实现过程中，采用随机优化搜索算法和禁忌搜索算法实现参数优化过程。对于输出变量论域，输出变量Kp、Kd的伸缩因子应与误差的单调性一致，而输出变量K的伸缩因子与误差的单调性相反，则输出论域的伸缩因子采用的一般公式为[9]：

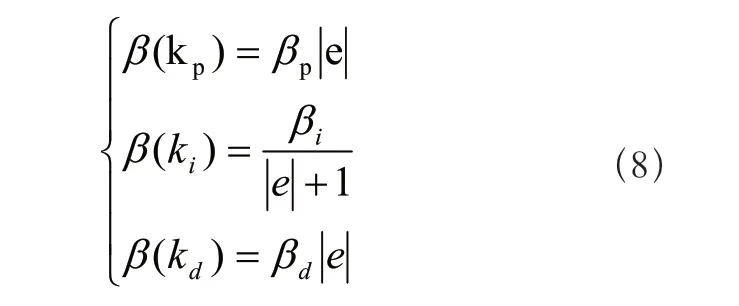
通过调试优化，参数选择如下：

3 实验验证及分析

电机的控制系统与实验台如图6、图7所示。实验系统包括以下部分：

图6 BLDCM电机控制系统

图7 实验平台

1）采用STM32F103RBT6控制芯片作控制核心。

2）驱动模块采用SD05M50DBE驱动芯片作为驱动电路。

3）输入电压为12V，输出电压为5V和3.3V的电源模块。

4）电机型号为57BL02，电机的主要技术参数如表2所示。

表2 电机参数表

同时，该实验平台控制系统采用反电势过零检测法检测转子位置[10]，通过合理的系统硬件电路，减少因系统硬件带来的检测误差，从而提升检测转子位置的灵敏度，并提高系统的可靠性。

电机输出的电机相电压波形如图8所示：

图8 启动200ms电压图

其中通道1、3、4分别对应三相绕组的电压。通过输出3个两两相差120°电角度的梯形波，从而实现对BLDCM的控制。

图9为转速为500rpm时的三相反电势信号，在该低速下电机的三相反电势过零比较信号如图10所示。当连续多次检测到开路相的反电动势过零点后，系统从他控式运行模式切换到无刷直流电机自控式模式。连续多次检测的目的是防止干扰等引起的误差检测和转速未达到预定转速，保证能够平稳切换，顺利完成启动过程。

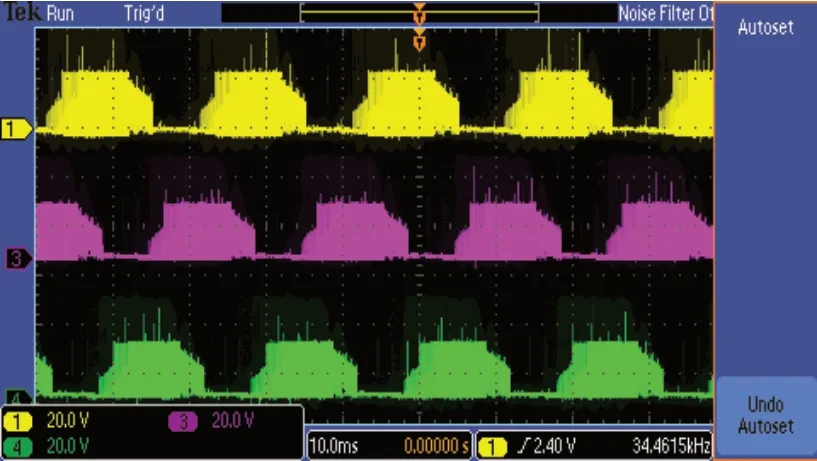
图9 三相反电势图

图10 三相反电势过零信号图

由此可以准确的得到电机的定子浮空相过零点时刻，反电势信号在电机高速时比电机低速时更容易检测，故本控制系统在高中低速都有良好的运行性能。相电压波形互差120度，电机运行稳定。

设置电机目标转速为1200rpm，启动电机，根据实验中的记录的转速数据，使用MATLAB绘制转速曲线图11所示：

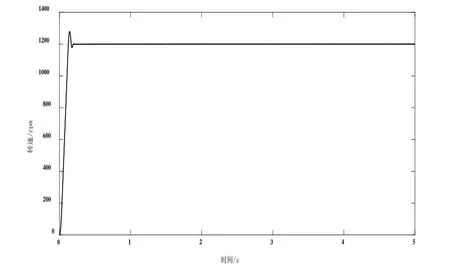
图11 速度响应曲线

由上图可以看出，当设定目标转速为1200rpm时，电机达到目标转速且稳定只需大约0.3s，并且超调量小。另外，设定不同目标转速，重复对比观察不同目标转速下的速度响应时间与超调量，可以发现电机在启动运行时系统调节时间短且超调量小的特点。实验可以证明该控制系统响应速度快，且控制精度高。

4 结语

本文构建的模糊PID双模控制器将模糊逻辑的智能性与PID控制相结合。将模糊控制和PID技术同时应用于无刷直流电动机的速度控制，启动时消除了部分峰值超调，提高了上升时间和稳定时间。稳定运行时减小了电机的转速波动。因此，这种控制器可以成为精确控制应用的理想选择。