基于规则学习的差异工件随机批调度策略

杨子豪，谭 琦，夏田林，戴 飞

（合肥工业大学 电气与自动化工程学院，合肥 230009）

0 引言

批处理机是一类在满足约束的前提下可以同时处理多个工件的设备，目前已广泛应用于制造业中，例如金属加工、半导体生产、纺织品染整作业等相关领域[1]。同时批处理问题也引起了众多学者的关注。Dupont等[2]研究了一类差异工件单机批调度问题，提出了两种启发式算法SKP（Successive Knapsack Problem）和BFLPT（Best-Fit Longest Processing Time）。Chen等[3]对于单机批调度问题，提出浪费比的概念，并以此为基础定义了批间距离度量，设计了一种分批约束聚类算法。Li等[4]针对不相容工件族的批调度问题设计了启发式算法来优化系统的最大延期时间。

在实际的制造系统中，加工制造过程存在很多不确定的随机因素，例如上游系统故障，加工订单随机到达等。调度过程中的随机事件往往使得原有静态调度方法具有不可预测性，无法达到理想效果。因此，考虑随机因素的调度模型是一种更贴近实际加工环境的调度模型。随机调度问题近年来引起众多学者的关注，然而基于随机批调度问题的研究目前还不多。Germs等[5]使用马尔科夫决策过程对一类订单随机到达的单机调度问题进行了研究，给出了最佳订单接受策略和批调度方案。Duenyas等[6]研究了不相容工件族随机到达的批调度问题，提出了一种启发式算法对平均单位时间成本进行优化。John等[7]利用动态规划的方法对工件到达时间随机的相容工件族批调度问题的进行求解，并给出一种启发式算法。上述研究仅仅考虑工件尺寸相同的情况，然而实际生产中工件尺寸的差异是必然存在的，这使得随机批调度问题更加复杂。本文考虑差异工件随机到达下的单机批调度问题，由于尺寸的差异，加工系统会不可避免的出现机器加工资源浪费的情况，同时工件成批的组合方式也更多，问题规模急剧增加。因此，如何在这种情况下合理调度随机到达的工件使加工率最大是本文的研究重点。

在实际生产调度中，由于启发式规则简单、易于实施从而得到了广泛的应用。但是，这些规则一般只用于特定调度环境，并不具备随着环境改变而变化的优化能力[8]，无法满足复杂问题的需求。

相比之下，强化学习在动态环境中有较好的优化能力，它能赋予系统一定的学习性，使系统能够根据当前环境（即生产环境）的性能反馈修正系统在动态过程中采取的行动，从而适应生产环境的变化。强化学习是一种重要的机器学习方法，由于它良好的自适应性，使其在实际中的应用也越来越广泛[9]。Shahrabi等[10]使用强化学习的方法解决作业车间工件随机到达的问题。Chen等[11]针对动态环境下汽车配装线的物料运输问题，利用强化学习中的Q学习对问题进行求解。Ou等[12]利用Q学习方法解决了一类利用龙门架装卸物料的调度问题，给出了最优龙门架移动策略。

尽管强化学习方法有较好的优化性能，但是当系统状态总数增多或可选行动集合变大时，算法的搜索空间将急速增长，这会大幅降低算法的优化能力。基于此，在综合考虑优化性能和计算效率的情况下，本文将启发式规则与强化学习相结合，在底层利用启发式规则直接调度系统加工，在上层使用强化学习方法为系统的每个状态搜索合理的规则。这样即避免了算法搜索空间过大，也避免了人工指定规则的主观性。

本文以提升系统加工率为目标，考虑有尺寸差异工件随机到达的批处理机调度问题。在分析问题模型的基础上，设计出两类启发式规则，并将其与Q学习相结合提出基于Q学习的启发式选择调度算法（Heuristic Q-learning HQ）。最后通过仿真实验将所提算法与原有算法进行对比，验证了所提算法的有效性。

1 系统模型

1.1 问题描述和假设

本文研究的随机批处理问题的系统模型如图1所示，系统的主体是一台容量为C的批处理机，可以一次加工尺寸之和不超过其容量的多个工件。系统配备具有传感器的分拣装置可以感知到达工件的类型，并配备m个容量为N的缓冲库用来存放不同品种的工件。

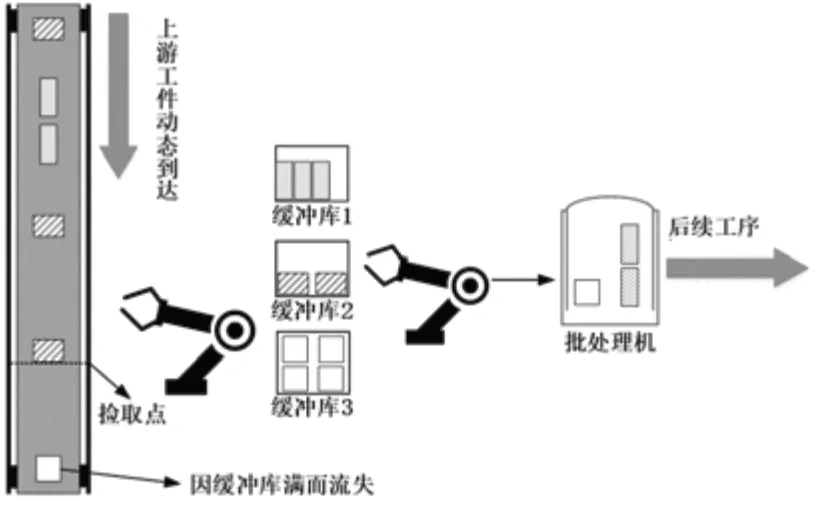
图1 差异工件随机到达下批处理系统示意图

各类工件不断地随机到达当前站点，ti和di分别表示第i类工件的加工时间和尺寸，分拣装置将到达的工件放入相应的缓冲库中等待加工。由于工件随机到达，系统需要实时的进行调度决策。系统的工作过程可概括为:在决策时刻，系统根据当前缓冲库状态选择加工一批工件或等待后续工件到达。当选择加工时，系统从缓冲库中选取一批工件放入批处理机中加工。当选择等待时，批处理机处于空闲状态，直到有后续工件到达系统。由于缓冲库容量有限，如果工件到达系统时，存放该类工件的缓冲库已满，则该工件流失。本文要解决的关键问题就是在决策时刻如何合理调度机器，减少系统生产代价，避免工件流失从而提高系统加工率。

为了有效描述该问题，同时做出如下假设：

1）每类工件按照泊松随机过程到达生产系统。

2）在满足容量约束的前提下，机器每次可加工由任意工件构成的批。

3）机器加工时间等于加工批中所有工件加工时间的最大值。

4）机器一旦开始加工则不允许中断。

1.2 决策过程

记ni为第i类工件在缓存库中的个数，也表示第i类工件在系统中的状态，其状态空间为Φi={0,1,...,N}，系统状态即为m类工件缓冲库容量所组成的联合状态，sn1,n2,...nm=｛n1,n2,...nm｝。在控制策略的作用下，系统从决策时刻T0=0开始工作，在第k个决策时刻Tk时，假设当前状态为sn1,n2,...nm，系统根据当前调度策略采取的行动为vsn1,n2,...nm。若此时vsn1,n2,...nm为等待，则机器闲置并等待下一工件到达，记下一个工件的到达时间为ωk，则系统下一决策时刻为Tk+1=Tk+ωk，若到达的工件为第i类工件，下一决策时刻的系统状态即为Sn'1,n'2,...,n'i,...nm，其中n'i=min{ni+1,N}。若vsn1,n2,...nm为加工一批工件，则系统从缓冲库中选出其指定的工件进行加工，记加工时间为τk，则系统的下一个决策时刻为Tk+1=Tk+τk，下一决策时刻的状态为Sn'1,n'2,...,n'm，其中n'i=ni-ai+bi，ai和bi分别表示本次决策时刻内第i类工件的加工个数和随机到达并存储的个数。

1.3 优化目标

本文的调度目标是提高系统加工效率减少生产代价。由于问题中各种类工件间存在着尺寸的不同，若用一定时间内加工的工件个数来衡量系统加工率显然是不合理的，因此借鉴文献[3]中的方法，引入工件量的概念对各类工件进行统一度量，一个工件的工件量等于其尺寸与加工时间的乘积。因此定义系统的加工率如下

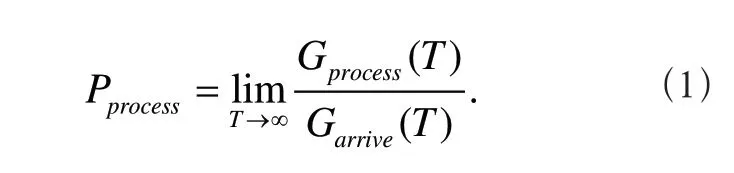
其中，Gprocess（T）和Garrive（T）分别表示在0到T时刻内加工的总工件量和到达系统的总工件量。

当系统稳定运行时，到达系统的工件要么被系统存储加工要么因缓冲库满而流失。因此，系统的工件量流失是优化的重要目标。另外从短期效益来看，提高加工时的机器利用率也能一定程度上提升加工率，同时在实际生产系统中也需要考虑少量的库存管理成本。因此，系统代价被定义为：工件量存储代价、工件量流失代价和机器浪费代价。其中在第k个决策周期内，将机器浪费代价定义为：

2 HQ调度算法

2.1 算法概述

由系统工作模式可知，批处理机的调度过程是由时间轴上一系列的决策所组成，系统需要在随机环境中不断的做出决策，因此可引入强化学习中的Q学习方法进行求解。考虑到本文提出的问题规模较大，所需算法不仅要有对随机系统较好的全局优化能力，而且要具备较高的计算效率。在本文中，只要满足批处理机容量约束的前提，任意组合方式形成的工件批都可以被系统作为动作进行加工。当批处理机容量较大或工件类型增多时，这种排列组合方式定义的可选动作将会非常多，Q学习的动作空间将急剧增加。这会导致算法的搜索空间激增，使得计算效率大幅降低。因此，本文在分析系统特性的基础上，设计出两类启发式规则作为Q学习行动来取代传统直接选取工件组合的行动，以提升算法的计算效率。同时，引入模拟退火搜索机制，提高算法的搜索能力。

2.2 启发式规则设计

本文设计的启发式规则分为两类:对缓冲库中所有工件完全分批后挑选特定批的选择式启发式规则和以基准工件构造成批的构建式启发式规则。系统在决策时刻选择某启发式规则作为行动，机器再根据该启发式规则调度工件进行加工。

1) 选择式启发式规则从全局角度考虑，对当前缓冲库中所有工件进行分批，然后再从分好的批中基于目标准则选取待加工批。因此，该类启发式规则优先考虑所有工件分批的优劣，使每个批尽可能的高效利用机器加工能力，在此基础上再考虑调度目标。在进行分批时，首先对缓存库中所有工件进行排序，排序方法按照工件加工时间由高到低。排序完成后，对序列利用Best-Fit方法进行分批，然后采用不同的选批规则从所有批中选一批工件进行加工。各选择式启发式规则的选批标准如下：

SPT-LPR（shortest processing time-largest proce-ssing rate，最短加工时间-最大加工率）规则

选择所有批中加工时间最短的批进行加工，若有多个批同时满足，则选择其中加工率最大的批进行加工，其中，加工率等于加工工件量与加工时间的比值。

LCW-SPT（least capacity waste-shortest processing time，最小加工能力浪费-最短加工时间）规则

选择所有批中机器加工能力浪费最小的批进行加工，若有多个批同时满足，则选择其中加工时间最短的批进行加工。

FB-LPR（fullest buffer-largest processing rate，缓存库存量最满-加工率最大）规则

选择所有批中含最满库存工件个数最多的批进行加工，若有多个批同时满足，则选择其中加工率最大的批进行加工。

LQ-SPT（largest quantity-shortest processing time，最大工件量-最短加工时间）规则

选择所有批中所含工件量最大的批进行加工，若有多个批同时满足，则选择其中加工时间最短的批进行加工。

2) 构建式启发式规则优先考虑要优化的目标，在缓存库中选择最符合规则优化目标的工件构成批，在此基础上再考虑该加工批的机器利用率的情况，并不考虑剩余工件的分批情况。各构建式启发式规则具体实施步骤如下：

FB（fullest buffer，存量最满）规则

Step1：在满足批的容量约束的前提下，从当前存量最大的缓存库中尽可能多的选取工件放入批中，若有多种工件的存量相同，则选择尺寸较大的工件类型；

Step2：计算批中剩余容量，在尺寸小于剩余容量的工件类型中选择存量最大的工件放入批中，重复该步骤直到没有工件可以放入批中为止。

FB-CPT（fullest buffer-closest processing time，存量最满-最相近加工时间）规则

Step1：在满足批的容量约束的前提下，从当前存量最大的缓存库中尽可能多的选取工件放入批中，若有多种工件的存量相同，则选尺寸较大的工件类型；

Step2：计算批中剩余容量，在尺寸小于剩余容量的工件类型中选择加工时间与当前批加工时间绝对值差最小的工件放入批中，若绝对值差相同，优先选择加工时间较小的工件，重复该步骤直到没有工件可以放入批中为止。

LPT（longest processing time，最长加工时间）规则

Step1：在满足批的容量约束的前提下，尽可能多的选择加工时间最长的工件放入批中，若有多种工件的加工时间相同，则选择存量最多的工件类型；

Step2：计算批中剩余容量，在尺寸小于剩余容量的工件类型中选择加工时间最长的工件放入批中，重复该步骤直到没有工件可以放入批中为止。

SPT（shortest processing time，最短加工时间）规则

Step1：在满足批的容量约束的前提下，尽可能多的选择加工时间最短的工件放入批中，若有多种工件的加工时间相同，则选择存量最多的工件类型；

Step2：计算批中剩余容量，在尺寸小于剩余容量的工件类型中选择加工时间最短的工件放入批中，重复该步骤直到没有工件可以放入批中为止。

LSTR（largest size time rate，最大尺寸时间比率）规则

Step1：在满足批的容量约束的前提下，尽可能多的选择工件尺寸与加工时间比率最大的工件放入批中，若有多种工件比率相同，则选存量最多的工件类型；

Step2：计算批中剩余容量，在尺寸小于剩余容量的工件类型中选择工件尺寸与时间比率最大的工件放入批中，重复该步骤直到没有工件可以放入批中为止。

要注意的是，若多个启发式规则在某系统状态下选出的待加工工件相同，表明这些规则在该状态下效果一致。为了避免行动冗余，应在Q学习选择动作前，从这些状态的行动集合中删除多余规则。

2.3 基于性能势的Q学习算法

Q学习的基本原理可概括为:决策主体与外界环境不断地交互，进行自主学习，通过观察系统状态转移信息（环境反馈）来迭代每个状态-行动对的Q值，进而学得最优或近优策略[13]。第k个决策周期的状态转移信息可表示为＜Sk,vSk,Sk+1,ΔTk,f(Sk,vSk,Sk+1)＞，其中，ΔTk和f(Sk,vSk,Sk+1)分别为状态的转移时间和转移所产生的代价。根据文献[14]中性能势的理论，平均准则下状态-行动对的Q值更新公式为：

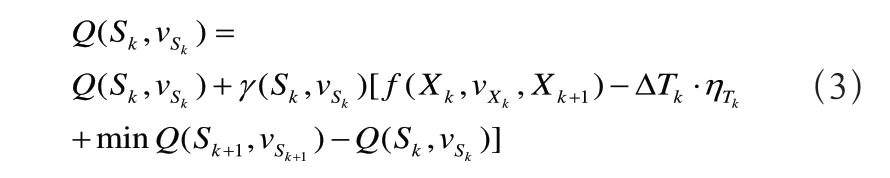
其中，γ（Sk,vsk）是Q值更新的学习步长，其随着访问次数增多而不断衰减，ηTk是系统平均代价的估计值。

f（Sk,vsk,Sk+1）的计算公式如下，当系统选择批处理机等待时，

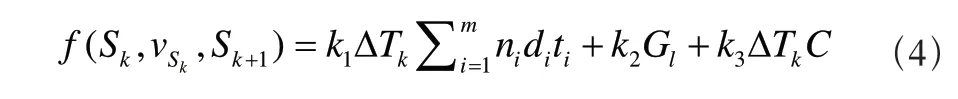
当系统选择批处理机加工一批工件时，

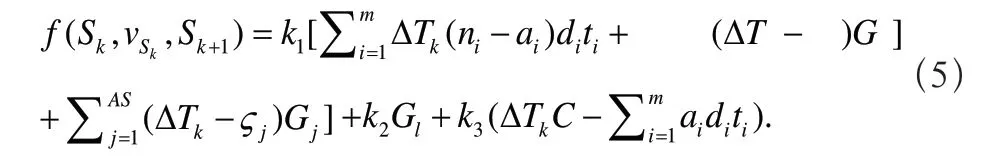
其中k1、k2和k3为存储代价、流失代价和机器浪费代价的权重，Gl为在转移过程中流失的工件量。AS为转移过程中到达并存储的工件个数，ςj和Gj分别为第j个工件的到达时间和工件量。

2.4 算法步骤

为了更好的平衡Q学习探索和利用的问题，本文引入模拟退火的Metropolis准则代替传统的贪婪策略（ε-greedy）来控制算法探索率。HQ调度算法具体实施步骤可概括如下。

Step1：初始化Q值表、每次迭代中学习步数Z，总迭代次数Y、模拟退火温度Ttemp和退火系数tςtemp。随机初始化系统状态，并令k=0，z=0，y=0。

Step2：根据当前状态Sk，分别计算出所有选择式和构建式启发式规则所对应的加工批;

Step3：若有多种启发式规则对应的加工批相同，则剔除多余相同的加工规则，由剩余规则组成该状态下的可选行动集合；

Step4：根据Q值表得到当前状态下的最优行动v*sk，即v*sk=argminQ（sk,v*sk），并从当前状态的行动空间中随机选取一个动作记为vrandsk。若exp{[Q（sk,v*sk）-Q（sk,vrandsk）/Ttemp]}＜rand(0,1)，则选择最优动作v*sk作为当前行动，否则随机选取一个行动vrandsk。

Step5：执行所选行动对应的启发式规则，观察状态转移信息并得到系统的下一状态Sk+1，根据式(4)或(5)计算转移代价并根据式(3)更新Q值表。令k=k+1，z=z+1。若z＜Z，则转跳到step2。

Step6：令y=y+1，若y＜Y，则令z=0，ζtempTtemp，并返回step2，否则算法结束。

3 仿真实验

实验中，将本文所提HQ算法与Q学习在工件品种数为3、4和5的情况下进行对比。用服务强度的概念（Traffic Intensity，TI）来定义工件的到达率，其公式为TI=∑m

i=1λiditi/C，其中λi即为第i类工件的泊松到达率。在参考文献[7]实验设置的基础之上，将品种数为3、4和5情况下的TI分别设置为0.85、0.95和0.95，其余系统参数设置如表1所示。由于品种数增多后，Q学习算法动作空间急剧增加，此时，为了保证传统Q学习的算法效果，在实验中加大Q学习的学习步数，虽然HQ可以避免该类问题，但为了确保实验合理，HQ仍与Q学习使用相同数据，如表2所示。

表1 系统参数设置表

表2 Q学习参数设置表

本实验由两部分组成：第一部分析两种方法的代价优化曲线和加工率优化曲线。第二部分对比在不同工件参数情况下HQ对于原Q学习算法的优化情况，验证所提启发式规则和HQ算法的有效性。

3.1 系统优化效果

Q学习和HQ每迭代一次，对当前学到的策略进行一轮评估，每轮评估利用当前学到的策略独立仿真10次，每次仿真50万步，取平均值作为当前策略对应的代价。仿真所用工件实例为d=(5,4,2)、(5,3,4,2)、(4,5,2,3,2)，t=(3,4,4)、(2,3,3,4)、(2,2,3,4,5)。在上述参数设置下，算法的系统代价优化曲线和加工率优化如图2、图3所示。

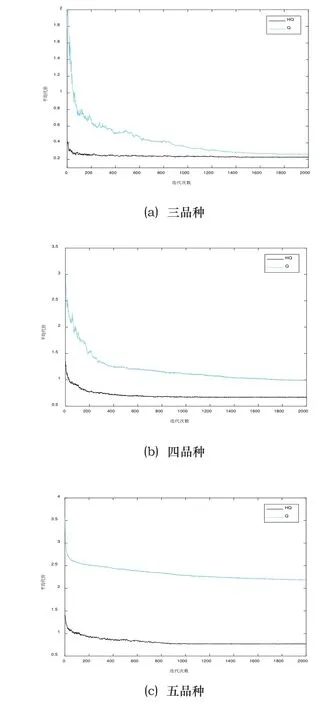
图2 平均代价优化曲线

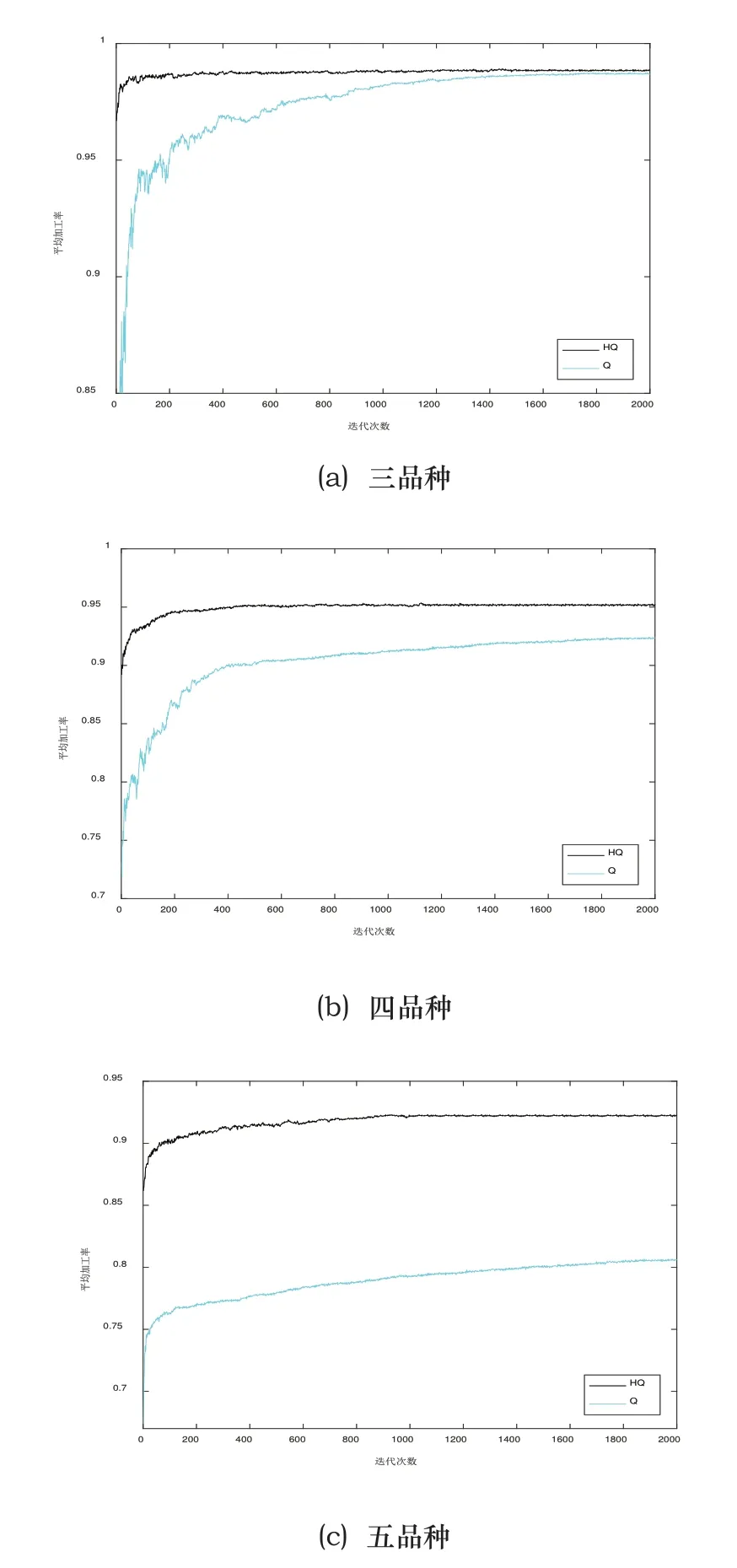
图3 加工率优化曲线

如图2所示，所有曲线在开始时急剧下降，这表明Q学习方法在前期使系统快速学习认知，并向最优或者近优方向调整动作。随着迭代次数增加，曲线下降速度逐渐变慢，系统代价收敛并稳定。图中表明，HQ算法要明显好于原始Q学习算法。在三品种算例下，Q学习最终在0.2528左右收敛，而HQ得到的系统最终代价约为0.2284。当工件种类为四类时，算法差距逐渐明显，HQ可将系统代价减小到0.6654左右，但Q学习最终收敛值只有1.0607左右。当品种增至五类时，若按照原有方法，系统共有22万个状态动作对等待更新，庞大的搜索空间和工件到达的随机性，使得Q学习已经很难对系统进行深度优化，而HQ只需为系统状态选择合适的规则，底层由提前设计好的启发式规则高效调度工件，这极大的提高了算法的优化效率。可以看出，HQ在刚开始就可以得到代价较小的调度策略，这是因为HQ所采用的动作是启发式规则，它们都是根据系统特性进行设计的，都有较好的求解效果，随着学习步数的不断增加，HQ算法逐渐为系统的每个状态找到适合的启发式规则，使得系统代价逐步降低。

与图2对应的系统加工率优化曲线如图3所示，在三品种下，Q学习经过长时间的学习优化也可以得到与HQ相近的加工率，此时HQ的优势主要体现在算法效率上。当工件种类增多后，算法差距开始明显加大。四品种时，Q学习的加工率从最初的70%增加到最终的92%左右，相比之下，HQ在很短的迭代步数内就将系统加工率提升到95%附近。五品种时，过于庞大的搜索空间已经很难再让Q学习对系统进一步优化，而HQ仍可以获得较高的系统加工率。

3.2 不同工件参数设置下算法优化效果

实际生产中，针对不同生产线和不同订单的需求，工件的尺寸和加工时间都会有所不同。下面主要验证算法在工件参数变化时的性能，为了直观展示算法改进效果，用GAP1和GAP2分别表示Q学习与HQ在系统代价和加工率上的差距。为了减少系统随机性的影响，将两种算法所学到的最终调度策略在每个算例上各运行50次，每次运行50万步，取其结果的平均值作为算法在该算例上的结果。3、4、5品种下各算例结果如表3、表4和表5所示。

由表3可以看出，在三品种的问题规模下，Q学习与HQ算法的差距不是特别明显，甚至在某些算例下，Q学习得到的结果要好于HQ。这是由于，首先在三品种规模下，按照传统排列组合方式定义的系统行动数并不会太多，并且系统的状态个数也较少，此时Q学习通过不断的迭代优化去搜索解空间可以得到一个较好的结果。其次，本文提出的启发式规则是针对一类问题进行设置的，其思想是在中大规模问题中可快速和简便的对问题进行求解，这些规则并不会根据特定算例进行优化，因此在小规模情况下，Q学习确实有可能在整个的工件排列组合空间中找到比启发式规则更好的策略，但上述情况很难在中大规模的算例中出现。从表4和表5的结果中可以看出，在问题规模扩大后，Q学习的优化效果开始明显降低，HQ的优势逐步体现出来。在四品种下，相比于Q学习，HQ最终使系统代价平均降低了53%，加工率平均上升4%，五品种时，HQ使加工率平均提升16%，并且两种算法在系统代价上的平均差距已经达到两倍以上。这充分表明了HQ算法和本文所设计启发式规则的有效性。

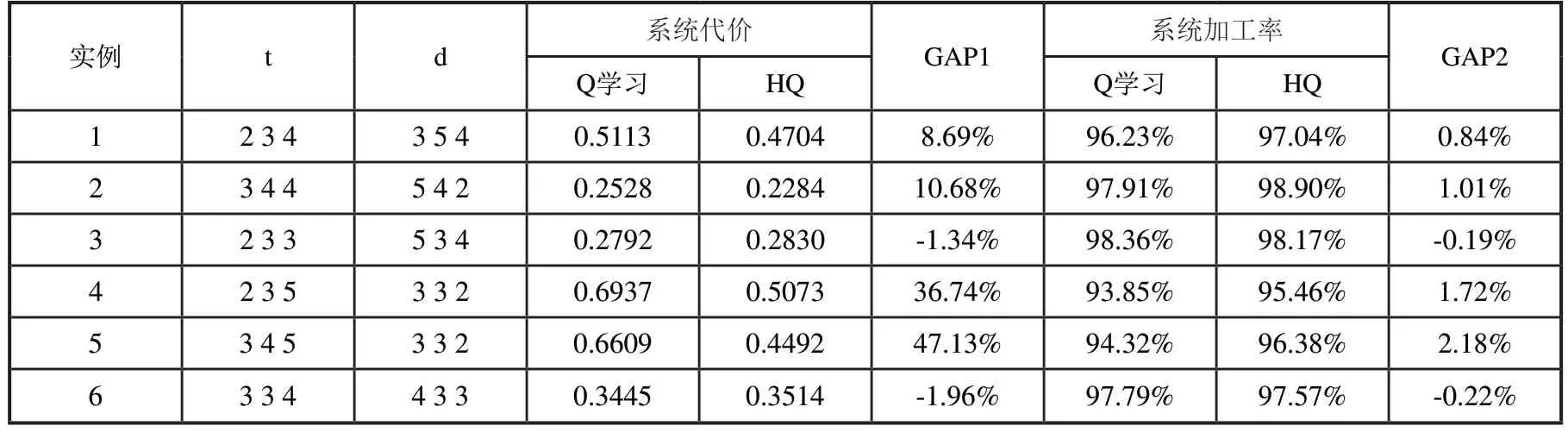
表3 三品种不同工件参数下各算法优化效果

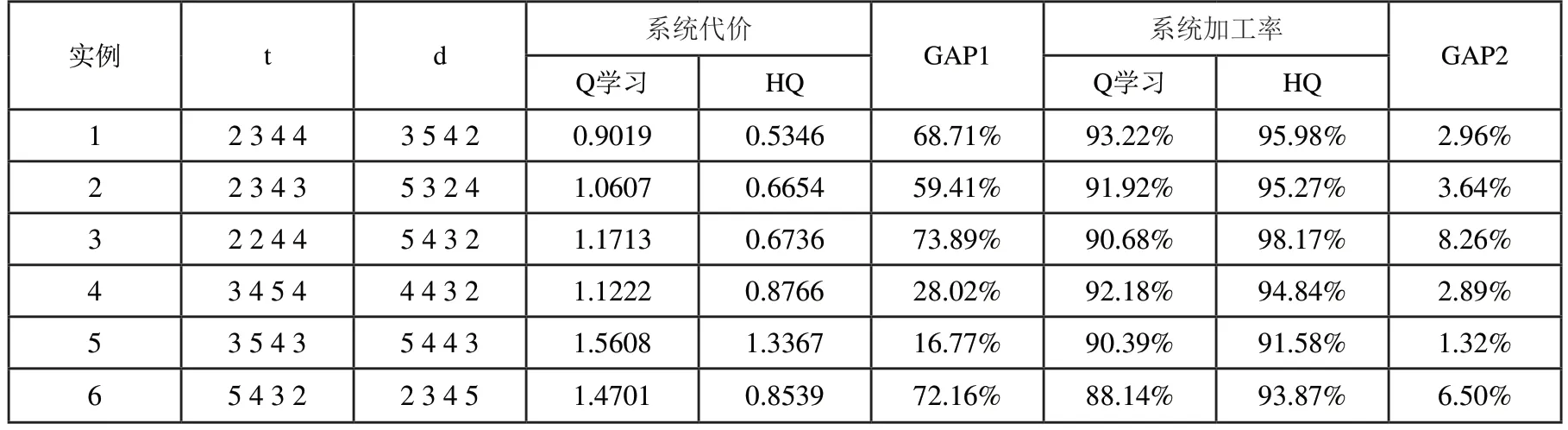
表4 四品种不同工件参数下各算法优化效果

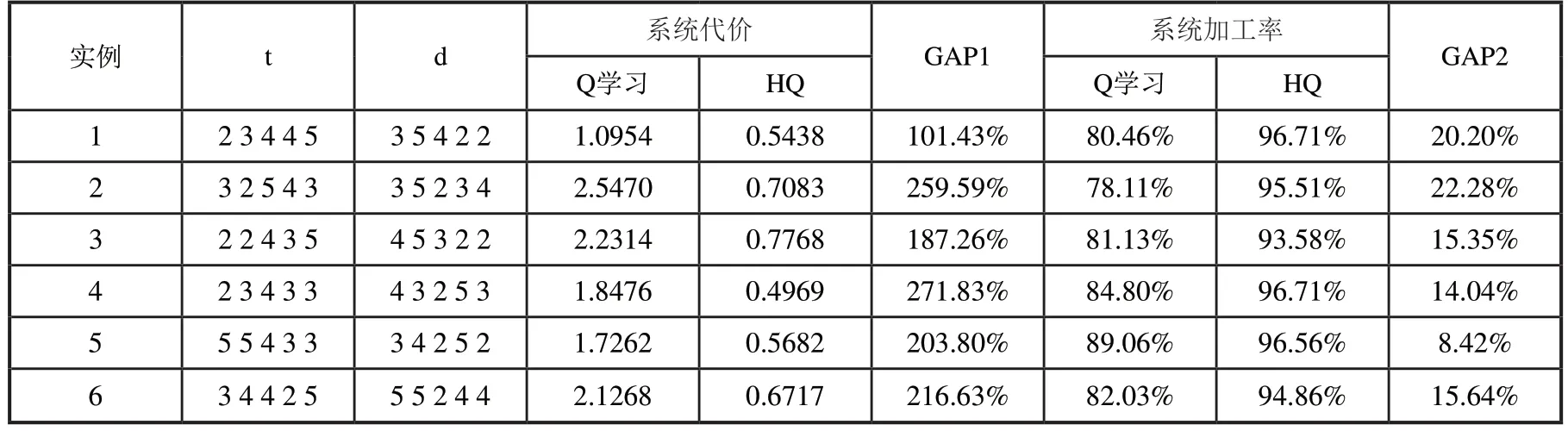
表5 五品种不同工件参数下各算法优化效果

上述分析表明，Q学习虽然有良好的无模型寻优能力，但是在面对搜索空间过大的情况时，求解效率明显降低，很容易陷入局部最优，在规模较大的问题下难以得到满意的求解效果。而HQ采用Q学习和启发式规则结合的方法，在底层根据系统特性设计高效的启发式规则调度工件，从而避免Q学习直接搜索工件组合造成算法搜索空间过大的问题，在上层使用Q学习为每个状态学得最优启发式规则规则，这也充分利用了在随机环境下Q学习的自主学习能力。HQ相当于结合了二者的优势，在提高算法效率的同时也充分利用了Q学习在随机环境下的学习能力。

4 结语

本文主要研究了具有尺寸差异工件随机到达系统情况下批处理机的优化调度问题。在建立系统优化模型的基础上，针对规模较大的情况，设计了两类启发式规则，并由此给出基于Q学习的启发式选择算法。实验表明所提算法有良好的求解效果，并且问题规模越大效果越明显。在后续研究中，可考虑诸如机器故障维护，加工时间不确定等更多的随机因素。