基坑吊脚墙支护中锁脚锚索的设计方法探讨

陈富强，杨光华, ，周沛栋，李支令，乔国龙

(1.广东省水利水电科学研究院，广州 510635； 2.广东省岩土工程技术研究中心，广州 510635；3. 华南理工大学土木与交通学院，广州 510640；4.广东省水利电力勘测设计研究院有限公司，广州 510635；5.广东粤海珠三角供水有限公司，广州 511458)

1 概述

一般情况下，基坑工程中的挡土结构(地连墙或桩)的嵌固深度需要满足整体稳定性验算、抗隆起验算、抗倾覆(踢脚破坏)稳定性验算和嵌固段基坑内侧土反力验算的要求，当坑底以下为软土时，其嵌固深度还需要满足绕最下层支点为轴心的圆弧滑动稳定性的要求。然而，当遇到上覆土层，下部岩层埋藏浅且强度很高的土岩组合地质条件，或者当基坑开挖很深，基坑底面已处于中风化甚至微风化的硬岩层中时，在基坑支护设计时，综合考虑到支护的经济性、工期和施工的难度等因素，通常采用“吊脚墙(桩)”支护。广东省地质条件多样性，决定了某深基坑工程支护形式的多样性，各种支护形式都在应用[1]，其中吊脚式支护结构在高层建筑(如广州东塔)、城市地铁(如广州地铁、东莞地铁)等的基坑工程中广泛应用[2-10]，但是其设计计算理论却还不成熟，国家和地方的基坑规范规程尚未有相关的设计条文。吊脚式支护的通常做法，为了保证“吊脚墙(桩)”墙(桩)脚的安全，在墙(桩)入岩面以下预留一定宽度的岩肩固定墙(桩)脚。但由于施工爆破等方面的影响，预留岩肩可能会被破坏，损失了对墙(桩)脚的支撑作用，此时，为了防止脚根不稳，导致造成墙底塌方，产生危险，往往会在吊脚墙(桩)底增加锁脚锚索来固住墙(桩)脚，可见，锁脚锚索的设计在吊脚墙(桩)支护设计中是至关重要的。李栋[11]等采用强度折减法研究了吊脚支护，指出护桩弯矩随工况的变化趋势，表明在基岩垂直开挖后，需重点关注锁脚锚杆轴力和预留岩肩的完整程度对二元岩土基坑稳定性的控制作用。

在吊脚墙(桩)设计计算的研究方面，刘建伟[12]根据吊脚桩支护体系受力原理和分步开挖工况，提出系统的“吊脚桩”支护体系计算模型，上部桩锚结构按“零嵌固”排桩模型计算，锁脚锚索通过抗踢脚稳定性计算其承载力，下部岩层基坑分别按复合土钉墙模型进行圆弧稳定性验算和岩质边坡模型进行平面稳定性验算。徐涛[13]等介绍了吊脚桩在广州地铁中的应用，将“吊脚桩”组合围护体系分成两部分，分别采用弹性增量法计算分析。从已有资料来看，若锁脚锚索的设计拉力通过极限平衡分析(如抗踢脚稳定)确定尚不合理，因为未考虑施工过程的影响，若以岩肩顶面处作为分界线，按“零嵌固”弹性支点法计算锚索拉力，则可能导致计算的锚索拉力偏小。因此，为了保证吊脚式支护结构的安全稳定，进一步完善锁脚锚索的设计方法是非常必要的。为此，本文对吊脚墙支护中锁脚锚索的设计方法进行了研究，提出了符合施工过程的设计计算方法，可供设计人员参考使用。

2 锁脚锚索设计计算原理

根据增量法的计算原理，在多支撑支护结构中，支撑或锚杆都是先开挖后支撑的，即支撑前结构已变形，且不同过程中其计算的力学体系也是不同的，为此，对多支撑的支护结构的受力，采用增量法进行计算才符合实际[14-15]。

为了分析方便起见，以图1的吊脚式支护体系为例，说明锁脚锚索的设计计算原理。与通常的做法一样，将吊脚式支护体系分成上、下两部分进行分析计算，为了分析锁脚锚索拉力的计算，取上部结构进行分析，计算模型如图2所示，即取岩肩顶面处的标高作为基坑的底面标高，支护墙(桩)按实际长度，计算模型中不加锁脚锚索，根据施工过程，用增量法计算至基坑底面，采用等效替代思想，此时基坑开挖面以下，岩层对支护墙(桩)坑底以下的抗力之和即为锁脚锚索需要提供的水平向拉力之和，可以理解为后期由于岩肩内侧的开挖，原本由岩肩对支护墙(桩)提供的抗力转移至了锁脚锚索，即力的转移，不考虑岩肩对支护墙(桩)的有利作用，将其作为安全储备考虑，设计计算的锁脚锚索的拉力是偏大的，故设计方案是偏安全，因此，采用此方法计算，可以避免判断按极限平衡分析确定的锚索拉力是否安全可靠的问题，避开了采用极限分析方法的缺点，且设计计算的锚索拉力是考虑了施工过程影响的，更符合基坑的受力和变形实际。

图1 吊脚式支护结构示意

图2 吊脚式支护结构(上部结构)示意

可见，由水平方向的静力平衡条件，作用在挡土构件嵌固段上的基坑内侧土反力合力=锚索的水平分向的合力，然后根据锚索的倾角，可以求得轴力计算值(见图3)：

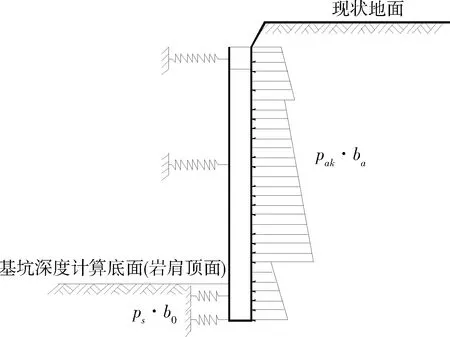
图3 吊脚式支护结构简化计算模型示意

T=∑Psb0

(1)

式中：

T——锚索的水平分向的合力，kN；

Ps——作用在挡土构件嵌固段上的基坑内侧的分布土反力，kPa；

b0——挡土结构的土反力计算宽度，m。

3 案例分析

以珠江三角洲水资源配置工程SL01#盾构工作井基坑支护为例。SL01#工作井外径为34.3 m圆形竖井，地面平整高程为44.0 m，基坑底高程为-4.88 m，开挖深度为48.88 m。采用地下连续墙+砼内衬墙及锚杆支护方案，地连墙墙厚为1 m，土层衬砌后内径为29.9 m，岩层衬砌后内径为26.8 m。上部采用地下连续墙和逆作法钢筋砼内衬墙支护，下部弱风化变质岩段井身采用预应力锚杆和逆作法钢筋砼内衬墙支护。其具体的基坑支护结构设计为：上部连续墙采用吊脚式，墙厚为 1.0 m，墙底嵌入弱风化岩不小于3.5 m，底部采用两层预应力锚索锁脚，锚索(5Φs15.2)单根长L=11 m，倾角为15°，布置间距为2.0 m×2.0 m；下部弱风化岩段锚杆(1Φ25)单根长L=6 m，倾角为15°，布置间距为1.5 m×1.2 m，并采用挂钢筋网喷砼(厚度250 mm)护面，平面和剖面示意如图4和图5所示。

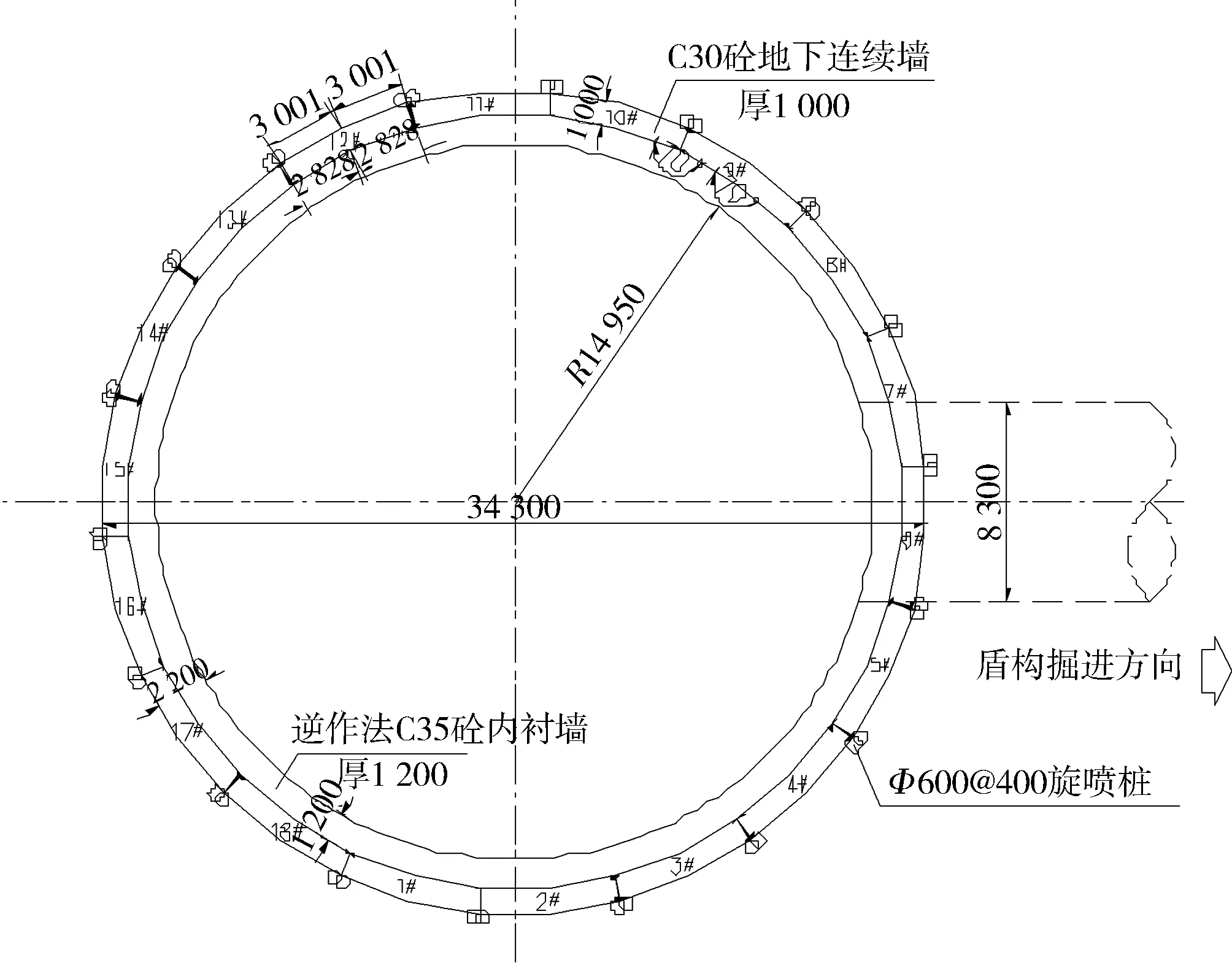
图4 SL01#工作井平面示意(单位：mm)

图5 SL01#工作井剖面示意(单位：尺寸mm，高程m)

基坑围护结构侧壁安全等级为1级，结构重要性系数为 1.1。始发井基坑周边施工超载按35 kPa控制，盾构机吊装布置于端头洞门侧，地面超载按70 kPa考虑；根据钻孔揭露，岩土层依次为人工填土，松散状填土，压缩性高，自稳能力差；坡积土，由泥质砂砾等组成，透水性较大，杂乱，压缩性高，易冲刷破坏；全风化变质岩，呈砂砾质粉质黏土状，黏粒含量低，韧性较差，干强度一般；强风化变质岩，强风化岩风化剧烈，岩体呈碎裂结构，夹有全风化夹层，整体稳定性差；弱风化变质岩，弱风化岩体为块状～整体状结构，岩质坚硬，完整性好。各层土的物理力学参数建议值见表1。

表1 各土层物理力学参数建议值

根据《港口工程地下连续墙结构设计与施工规程》(JTJ 303—2003)中圆形支护地下连续墙结构设计的有关规定。圆形支护地下连续墙结构宜按空间结构计算，也可按轴对称结构取单位宽度的墙体作为竖向弹性地基梁计算。墙体和环梁的环向效应，可按轴对称结构简化为等效弹性支撑。

当圆形支护地下连续墙结构利用环梁作支撑时，可将环梁的作用以等效支撑弹簧来替代(如图6所示)。单位宽度墙体上环梁的等效弹性支撑系数可按式(2)计算：

a 环梁支撑 b 等效支撑弹簧

(2)

式中：

Kh——环梁的等效弹性支撑系数,kN/m2；

Eh——环梁材料的弹性模量,kN/m2；

Ah——环梁截面面积,m2；

Rh0——环梁中心线初始半径,m。

圆形支护墙体的环向效应可采用分布的支撑弹簧来替代(如图7所示)。单位宽度地下连续墙墙体的等效分布弹性支撑系数可按式(3)计算：

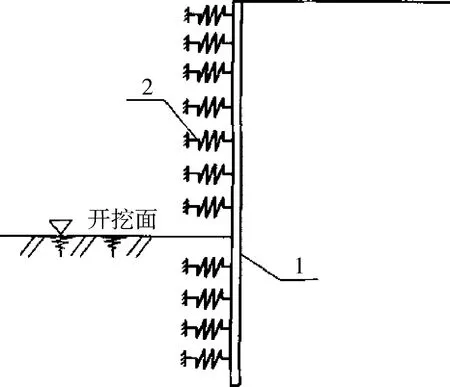
1-地下连续墙墙体；2-等效分布支撑弹簧

(3)

式中：

Kd——墙体的等效分布弹性支撑系数，kN/m3；

Ed——地下连续墙环向综合压缩模量，kN/m2，Ed=αE，E为地下连续墙混凝土弹性模量，kN/m2，α=0.5～0.7，本次分析中取α=0.5，当R0较大，或槽段数较多时取小值；

b——地下连续墙的墙体厚度，m；

R0——墙体中心线半径，m。

采用北京理正深基坑软件增量法计算，计算深度取32.5 m，即锁脚锚索所在的内衬墙底面，嵌固深度为3.5 m，计算结果如图8所示。

图8 增量法计算结果示意

计算至开挖底时，作用在挡土构件嵌固段上的基坑内侧土反力合力∑Psb0=529 kN/m(如图9所示)，设计了两排锚索，锚索(5Φs15.2)单根长L=11 m，倾角为15°，水平间距为2 m，根据前面的锁脚锚索的计算方法，则每根锚索的轴力T=529 kN/m×2 m÷2根÷cos15°=548 kN，根据施工图，设计的锚索锁定值为550 kN。由于现场没有布置锁脚锚索的拉力监测，但从现场测斜监测数据来看，实测的最大水平位移为8.68 mm(如图10所示)，小于计算的最大位移为12.58 mm，可见，锚索的设计还是合理、可靠的。

图9 各工况下基坑内侧土反力合力计算结果示意

图10 现场监测测斜累计位移示意

3 结语

针对目前吊脚式支护中锁脚锚索拉力设计方法尚缺少有效计算方法的现实问题，本文从吊脚式支护结构受力的实际出发，分析了锁脚锚索的受力过程，从力的转移的角度，提出了将坑底以下基坑内侧土反力合力等效为锁脚锚索的水平拉力之和，并以一个实际工程的锁脚锚索设计为例，分析了计算过程，通过监测数据对比，初步验证了方法的可行性。本文提出的锁脚锚索的计算方法是考虑了施工过程影响，由此计算的基坑支护的受力和变形更符合工程实际，是一种比较可靠的计算方法，可供类似工程设计参考。