400 km/h高速铁路隧道洞口等截面无开孔扩大型缓冲结构气动效应分析
2021-11-04王维洲钟登朝梅元贵
王维洲 钟登朝 胖 涛 梅元贵
(1.兰州交通大学甘肃省轨道交通力学应用工程实验室, 兰州 730070;2.中铁二院工程集团有限责任公司, 成都 610031)
高速列车驶入隧道产生初始压缩波,压缩波以音速传播至隧道出口处向外辐射形成压力脉冲波,使得洞口外产生“轰鸣声”,强度足够大时还会产生音爆,严重影响隧道周围环境和居民生活。针对这一问题,国内外专家、学者开展了大量的试验和研究工作。日本学者发现列车进入隧道产生的压缩波最大压力梯度近似与车速的3次方成正比,提出在隧道进口端加装缓冲结构的措施,并系统研究了开孔型的喇叭口扩大型和等截面扩大型缓冲结构,有效地解决了既有速度下的微气压波问题[1-3]。德国学者Hieke等针对300 km/h隧道微气压波问题,研究了洞口斜切、两侧开孔和顶部开孔等缓冲结构,并进行了线路测试验证[4-5]。法国学者Rety等研究了缓冲结构洞门斜切角度对列车进入隧道引起压缩波梯度的影响规律[6],Uystepruyst等研究了圆锥及抛物线渐变扩大断面和等截面扩大型无开孔缓冲结构的减缓气动效应,并给出了等截面扩大断面面积与隧道断面面积之比在不同速度等级下(250~400 km/h)的优化值[7]。英国学者Vardy等采用动模型试验方法研究了两侧开孔的长大缓冲结构,并进行了大小孔的比较[8]。中国学者陶伟明研究了洞口缓冲结构、洞身辅助坑道和隧道群开口连接明洞对微气压波的减缓效果[9],马伟斌等总结了多条线路的微气压波测试结果和变化规律[10],吴剑等总结了300~350 km/h高速铁路双线隧道压缩波的洞内传播激化特征[11],赵勇等总结了350 km/h隧道缓冲结构的型式、参数和气动效应[12],也得出了高速列车进入大断面双线隧道产生的压缩波最大梯度和微气压波与列车速度的3次方成正比的结论[13]。
截至目前,针对400 km/h隧道微气压波的研究较少,而400 km/h隧道微气压波问题更为严重,对隧道的防治措施也提出了更高要求。基于此,本文采用基于CFD软件的三维可压缩非定常湍流流动有限体积法和重叠网格法,研究400 km/h高速列车进入未设缓冲结构、设置无开孔等截面、无开孔扩大断面型缓冲结构隧道的初始压缩波波形和压力梯度的变化规律,比较了不同缓冲结构断面面积与隧道断面面积比值对压缩波波形和降低压力梯度的影响规律,本文研究结果可为400 km/h隧道缓冲结构和设计提供基础。
1 研究方法
本文采用STAR CCM+流体仿真软件进行数值计算。模型计算采用的控制方程为三维可压缩非定常的N-S方程,离散方法采用有限体积法,湍流模型选用k-SST模型。网格生成采用重叠网格方法,壁面采用全y+壁面处理。
重叠网格法将计算区域划分为背景区域和重叠区域,重叠区域包含列车。设置Free Stream边界、wall边界、overset边界3种边界条件。地面、车体、缓冲结构和隧道为wall边界,车体周围为overset边界,其他为Free Stream边界。受网格数量的限制,本文忽略了道床和轨道对高速列车通过隧道和缓冲结构时产生压力波的影响。
初始条件:列车运行速度为400 km/h,远场压力值取为 101 325 Pa,参考温度为288 K。列车采用光滑启动的方法从静止状态加速到运行速度,然后包含列车的重叠区域保持匀速状态运行直至设定的计算时刻结束。
2 计算模型及计算域
2.1 动车组计算模型
本文采用国内400 km/h某型4节编组动车组的全尺寸模型,列车模型保留了转向架和风挡,忽略了受电弓。模型全长209 m,列车车高4.1 m,鼻长12 m,截面面积为11.88 m2。
2.2 计算域及网格划分
本文的计算域高100 m,宽200 m,长803 m。选取长200 m的双线隧道,隧道内净空面积为100 m2。为减少网格数量,节省计算资源,采用分区域划分网格的方法,对背景区域和重叠区域分别进行合理的网格划分。划分网格时,流场变化不大的空间网格尺寸较大,在流场变化剧烈的空间(如缓冲结构、头车、车尾、转向架以及风挡等)设置加密块,同时要求不同网格尺寸之间平稳过渡,保证网格数量在各个空间的合理分配,避免网格数量过大导致计算迭代误差过大。此外,为提高计算精度,在车体表面、风挡、隧道壁面处生成了边界层网格。
3 计算结果与分析
3.1 初始压缩波的形成
将动车组进入缓冲结构的时刻定义为零时刻,动车组进入缓冲结构时隧道内的压力分布如图1所示。由图1可以看出,t=-0.108 s时,列车鼻尖距离缓冲结构洞口1个鼻长,缓冲结构内压力开始升高,靠近列车的缓冲结构壁面大于远离车体一侧的压力,越靠近缓冲结构洞口压力变化越大,压力梯度就越大,此时隧道内壁面受到列车引起压力增大的影响还不明显。t=0时,列车车头刚好到达缓冲结构洞口,缓冲结构内压力继续升高,隧道内壁面的压力也开始升高,靠近列车的缓冲结构壁面远大于远离车体一侧的压力,初始压缩波正在形成。t=0.216 s时,列车驶入缓冲结构2个鼻长的距离,车头前方空间压力持续增大。进入缓冲结构洞口一段距离后,隧道壁面等压线从“斜切式”形状变成“正切式”形状,压缩波从三维效应变成一维平面波。t=0.432 s 时,列车驶入隧道1个鼻长的距离,车头前方空间压力增量接近饱和。
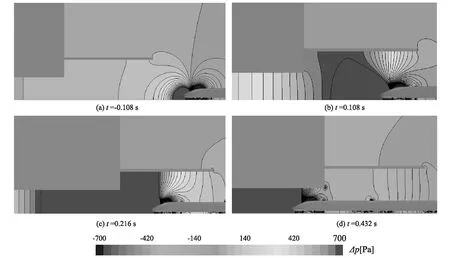
图1 列车进入缓冲结构的压力分布图
3.2 不同速度下无缓冲结构对比
350 km/h和400 km/h速度下的压力时间历程曲线如图2所示, 350 km/h和400 km/h速度下的压力梯度时间历程曲线如图3所示。由图2和图3可以看出,400 km/h速度下的初始压缩波峰值比350 km/h速度下的初始压缩波峰值增大了32%,相应地,最大压力梯度增大了35.8%。

图2 350 km/h和400 km/h速度下压力时间历程曲线图
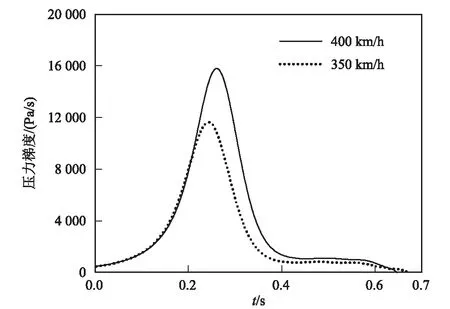
图3 350 km/h和400 km/h速度下压力梯度时间历程曲线图
3.3 缓冲结构的不同形状研究
断面形状为方形和拱形的缓冲结构与隧道的断面面积之比均为2.6,长度为3倍的鼻长。隧道内距离隧道口7D(D表示隧道的水力直径,取10.64 m)的隧道顶部中央测点处,拱形和方形缓冲结构的压力时间历程曲线和压力梯度时间历程曲线分别如图4、图5所示,压力幅值和梯度变化如表1所示。由图4可以看出,有缓冲结构的压力波波形要复杂得多,且压力有3次明显的跃升。t=0时,列车进入缓冲结构,产生初始压缩波,产生第一次压力跃升;t=0.32 s时,压缩波传播到隧道内测点位置,t=0.324 s时,列车到达隧道入口,阻塞比增大,产生第二次压力跃升;t=0.54 s时,压缩波传播到隧道内测点位置,当初始压缩波到达隧道入口时,一部分以压缩波的形式传播进隧道内,一部分以膨胀波的形式反射回缓冲结构洞口,再从缓冲结构洞口以压缩波的形式反射回隧道内,产生第三次压力跃升。t=0.754 s时,压缩波传播到隧道内测点。
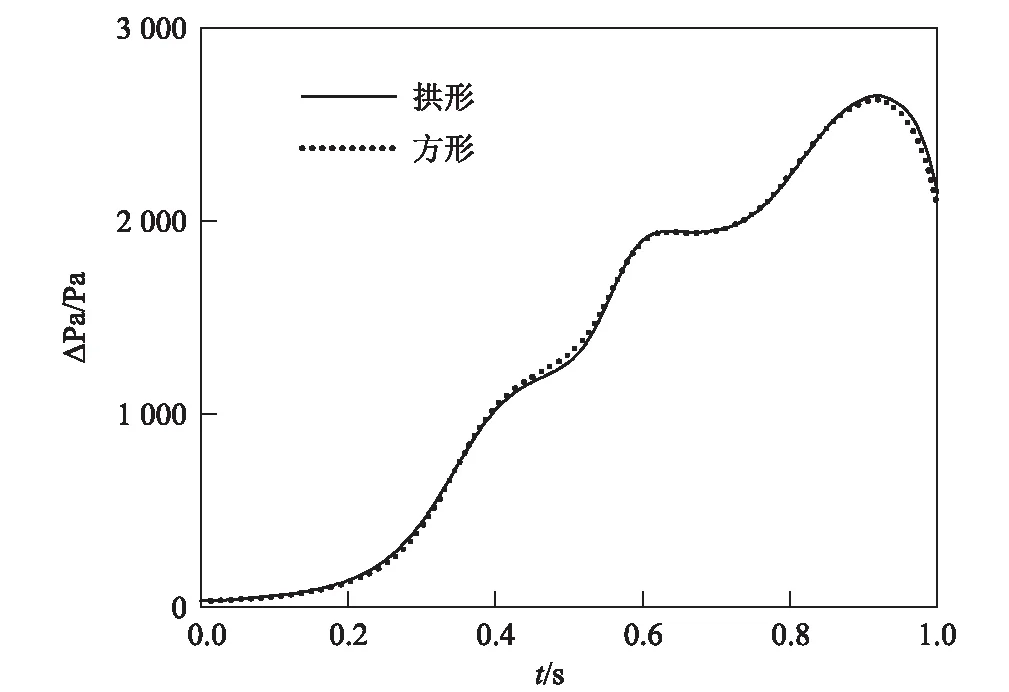
图4 不同缓冲结构形式的压力对比图
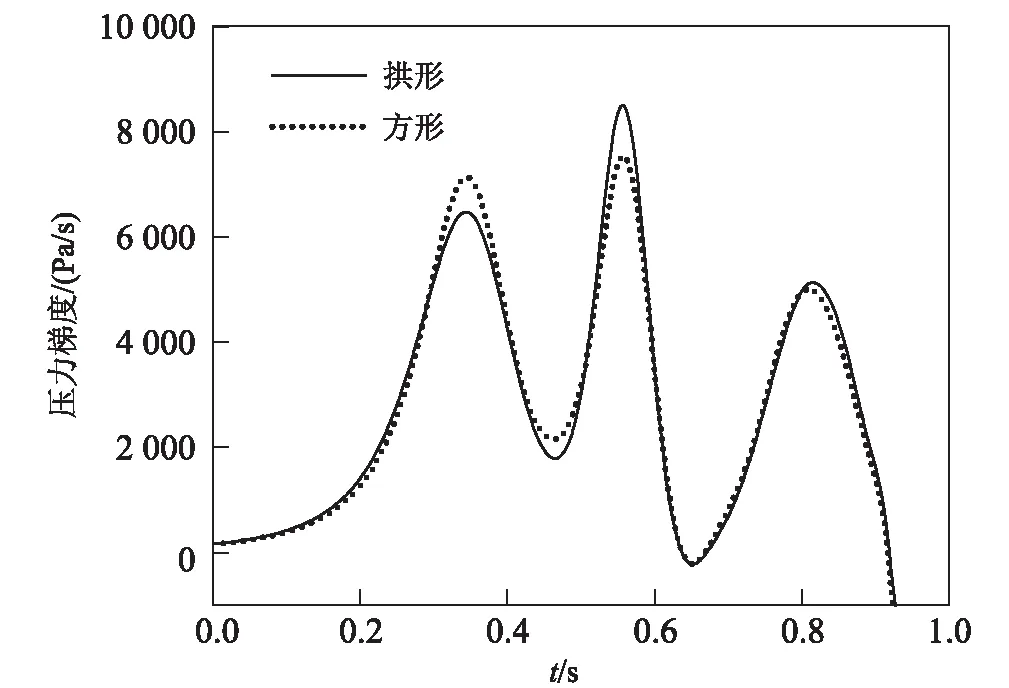
图5 不同缓冲结构形式的压力梯度对比图
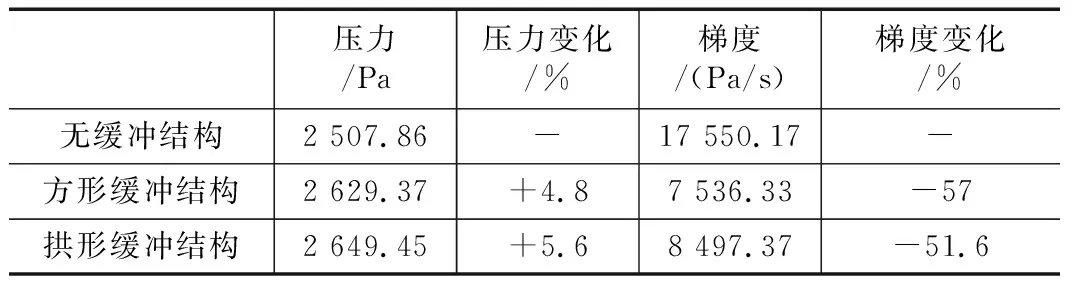
表1 压力幅值和梯度变化表
由表1和图5可以看出,与无缓冲结构相比,方形缓冲结构对初始压缩波的压力梯度峰值减小了57%,拱形缓冲结构对初始压缩波的压力梯度峰值减小了51.6%;与无缓冲结构相比,方形缓冲结构的初始压缩波峰值增大了4.8%,拱形缓冲结构的初始压缩波峰值增大了5.6%。因此,方形缓冲结构对初始压缩波的减缓效果优于拱形缓冲结构。
3.4 缓冲结构的不同断面比研究
在方形缓冲结构型式的基础上,对不同断面积比进行数值模拟分析。不同断面比缓冲结构压力对比如图6所示,不同缓冲结构形式压力梯度对比如图7所示,不同断面比压力幅值和梯度变化如表2所示。由图6、图7和表2可以看出,3种不同断面比的缓冲结构都对初始压缩波有减缓效果,其中断面比为2.6的方形缓冲结构对初始压缩波的减缓效果最佳,压力梯度减小了57%;断面比2.8的减缓效果次之,达到了53.3%;断面比2.0的减缓效果最小,减小了44.8%。在初始压缩波峰值方面,断面比越大,初始压缩波的峰值就越大,断面比2.0、2.6、2.8方形缓冲结构的初始压缩波峰值分别增大了3.1%、4.8%、5%。
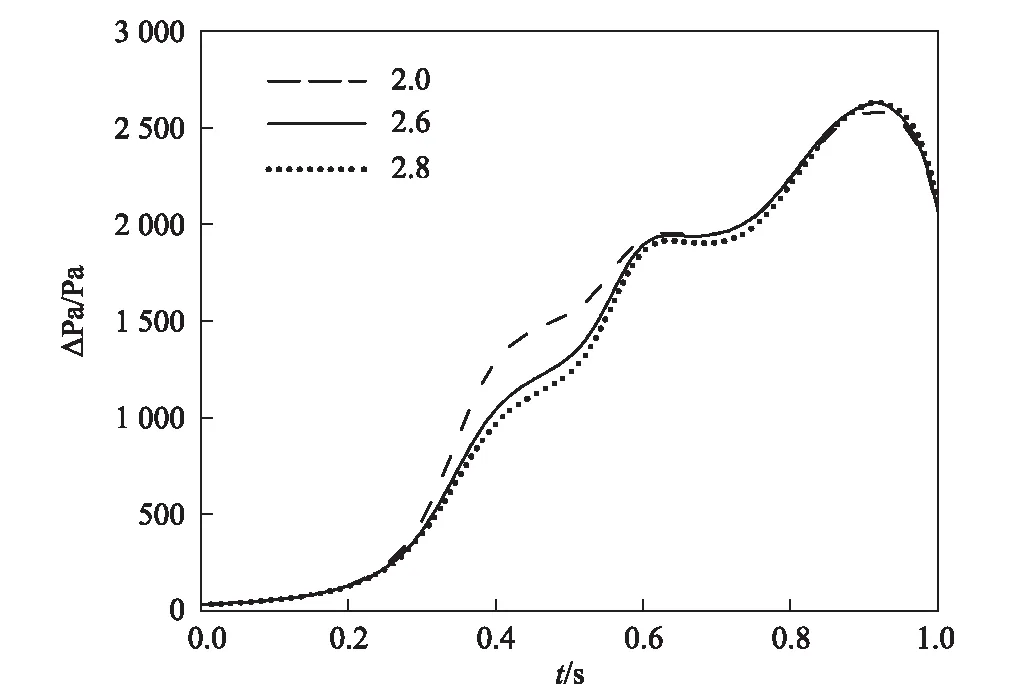
图6 不同断面比缓冲结构的压力对比图
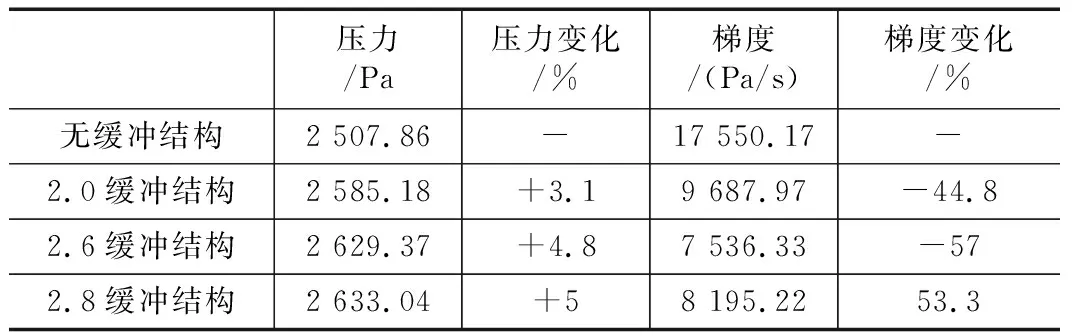
表2 不同断面比压力幅值和梯度变化表
4 结论
本文采用CFD软件的三维数值模拟方法,研究了400 km/h高速列车进入隧道产生的初始压缩波特征,在对350 km/h和400 km/h速度下无缓冲结构压缩波分析的基础上,研究了等截面无开孔扩大断面型缓冲结构不同形状、不同断面积比对初始压缩波的影响规律,得出主要结论如下:
(1)列车运行速度越高,列车进入隧道时产生的初始压缩波峰值越大,相应的压力梯度也越大,隧道入口增设缓冲结构对初始压缩波特别是最大压力梯度有很好的减缓效果。
(2)在断面比同为2.6时,方形缓冲结构对初始压缩波的减缓效果达到57%,拱形缓冲结构的减缓效果为53.3%,因此方形缓冲结构比拱形缓冲结构对初始压缩波压力梯度的降低效果更好。
(3)当列车速度为400 km/h时,断面比为2.0、2.6、2.8的方形缓冲结构对初始压缩波的减缓效果分别为44.8%、57%、53.3%,因此方形缓冲结构的最佳截面比为2.6。
