400 km/h动车组车体压力载荷隧道参数影响特征研究

王志钧 李 艳 魏 康 梅元贵 魏德豪

(1. 兰州交通大学甘肃省轨道交通力学应用工程实验室， 兰州 730070；2. 中铁二院工程集团有限责任公司， 成都 610031)

高速列车驶入隧道时，运行引起的空气流受列车和隧道壁的限制被瞬间挤压导致压力突变，产生隧道内空气压力波，该压力波作用于列车和隧道结构即产生气动载荷。气动载荷的反复作用会使车体及隧道衬砌等产生气动疲劳，降低其使用寿命，严重时甚至会危害列车运行安全。同时，压力波传入车厢还会引起旅客耳鸣、耳朵疼痛等压力舒适度问题[1]。

国内外采用实车试验、动模型试验和数值方法等研究了既有速度等级下高速列车隧道压力波的形成机理、影响因素及主次关系[2]，为列车设计和运维提供了技术支持，提出了250 km/h、350 km/h等级铁路隧道压力波效应的标准[3-7]，得出列车速度、阻塞比、隧道长度、列车长度及是否交会等是影响压力波幅值的主要因素[8-10]。隧道压力波数值方法主要有基于CFD软件的三维流动模型方法和基于特征线的一维流动模型方法。三维流动模型方法可模拟得出车外特别是列车头尾端及底部等的流场及气动载荷，但其计算成本较高，研究成果仅限于长度几千米的隧道；一维流动数值模拟方法可快捷得出批量、多参数的隧道压力波特征及规律，为车体气动载荷、舒适性和隧道净空面积比选等提供可靠依据[10-11]。

目前，国内外已开始研发400 km/h及以上速度的高速铁路列车[12-13]，但对该速度等级下隧道压力波及车体气动载荷等的研究还有待进一步开展。本文采用一维非定常可压缩不等熵流动模型特征线数值模拟压力波方法，研究400 km/h铁路隧道压力波的形成机理以及隧道长度和隧道净空面积对最大正负压值和最大压力峰峰值的影响规律，并验证了最不利隧道长度估算公式的合理性，归纳得出车体压力载荷的基本分布特征，为今后深化和系统研究压力载荷变化提供基础。

1 研究方法

高速列车通过隧道时，隧道内产生三维的非定常紊流流动，由于隧道长度远大于隧道断面的水力直径，同一隧道断面上的压力波动可近似相等，即隧道内压力波动具有一维特性。故可将列车通过隧道时隧道内产生的流动看作一维可压缩非定常流并建立一维流动模型，应用黎曼变量特征线法求解方程组，最终求得车外压力，具体求解方法可见参考文献[1]。其中，连续性方程为：

(1)

动量方程为：

(2)

能量方程为：

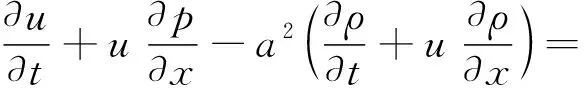
(3)

式中：u——空气流速；

p——空气压力；

κ——空气比热比；

ρ——空气密度；

a——当地声速；

F——空气流道横截面积；

G——空气与壁面的摩擦项；

q——空气与壁面的传热项；

ξ——空气与列车车壁的摩擦功；

t——时间。

具体计算参数如表1、表2所示。

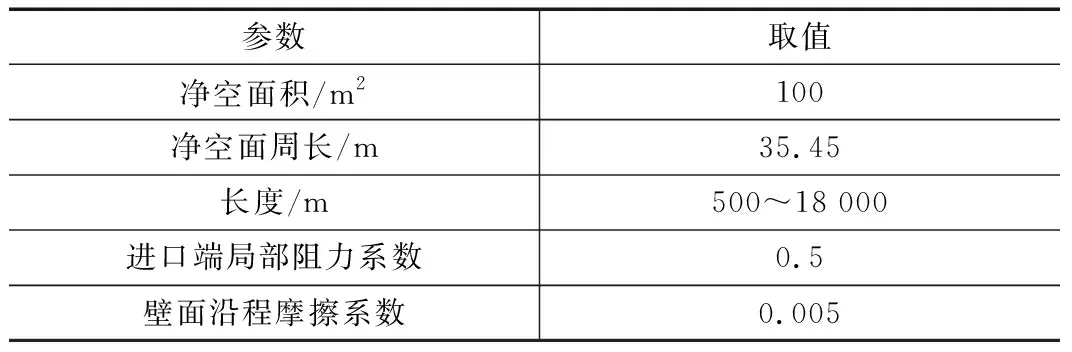
表1 隧道计算参数表

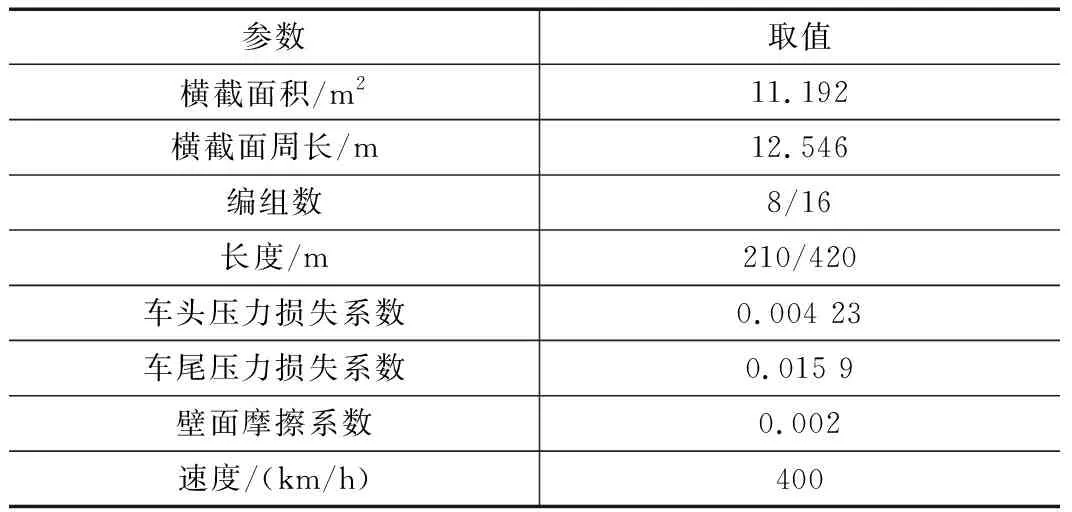
表2 列车计算参数表

2 计算结果和分析

2.1 列车隧道内诱发压力波形成机理

2.1.1 单列车通过隧道

8节编组(长210 m)动车组以400 km/h通过长4 000 m 隧道时，列车运行轨迹和隧道内压力波反射的叠加如图1所示。该情况下的头车车外压力时间历程曲线如图2所示。

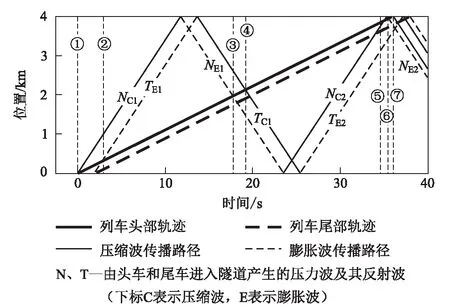
图1 列车运行轨迹和压力波反射叠加图

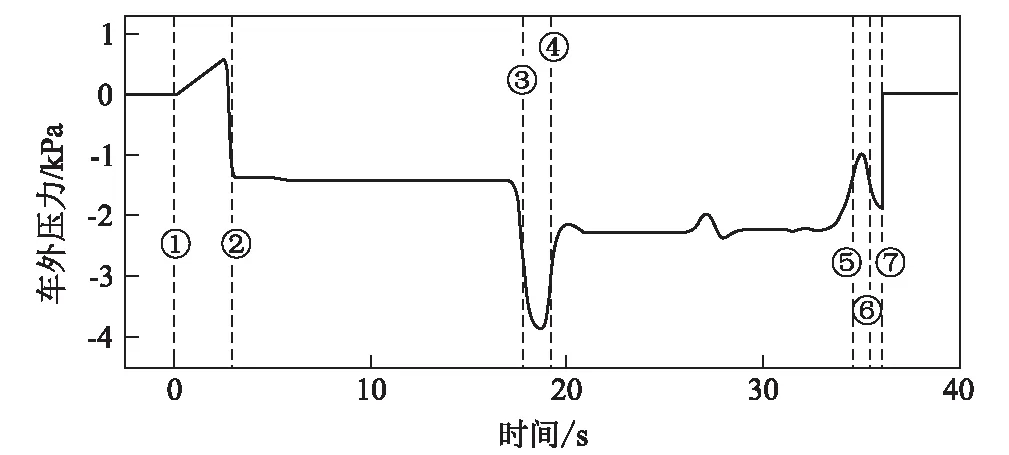
图2 头车车外压力时间历程曲线图

从图1、图2可以看出：

(1)列车头部于①时刻驶入隧道，因隧道空间限制了空气流动且空气具有可压缩性，车前空气受到压缩，一部分空气沿车体与隧道壁面形成的环状空间向后流动，另一部分空气受到列车头部压缩，产生压力增量，使得车外压力突然升高，产生压缩波NC1。列车尾部于②时刻驶入隧道，沿列车与隧道间环状空间向后流动的空气流动至车尾，流动空间突然增大，导致在车尾处产生负压，由此产生膨胀波TE1，使得车外压力突然降低。

(2)压缩波NC1和膨胀波TE1以近似当地声速向隧道出口端传播，到达隧道出口端后分别转化为相反形式波形NE1和TC1向隧道入口端反射，到达入口端后又转化为NC2和TE2再次反射，形成了隧道内复杂的压力环境。

(3)列车头车分别在③、④、⑤、⑥时刻与压力波NE1、TC1、NC2、NE2相遇，引发车外压力于③、⑤时刻突然上升，于④、⑥时刻突然下降。

(4)列车头部于⑦时刻驶出隧道，产生出口压缩波，车外压力急剧上升并恢复到进入隧道之前的水平。

2.1.2 隧道中央等速交会

两列车以400 km/h速度在长4 000 m的隧道中央等速交会时，列车运行轨迹和压力波反射的叠加如图3所示，图中线型与符号的含义与单列车通过隧道相同。为加以区分，称正向行驶的列车为“观测列车”，反向行驶的列车为“对向列车”。本文着重分析对向列车进入隧道产生的压力波对观测列车头车外压力的影响，该情况下观测列车头车车外压力的时间历程曲线如图4所示。

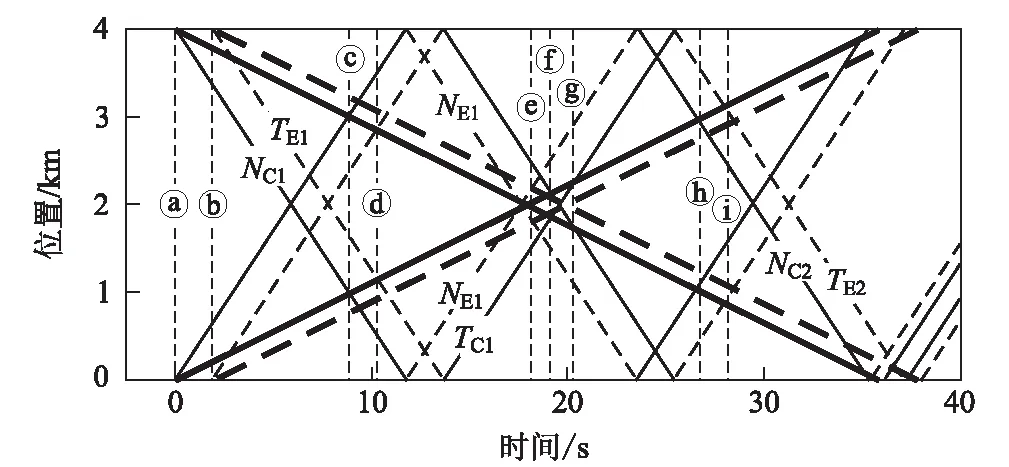
图3 列车运行轨迹和压力波反射叠加图

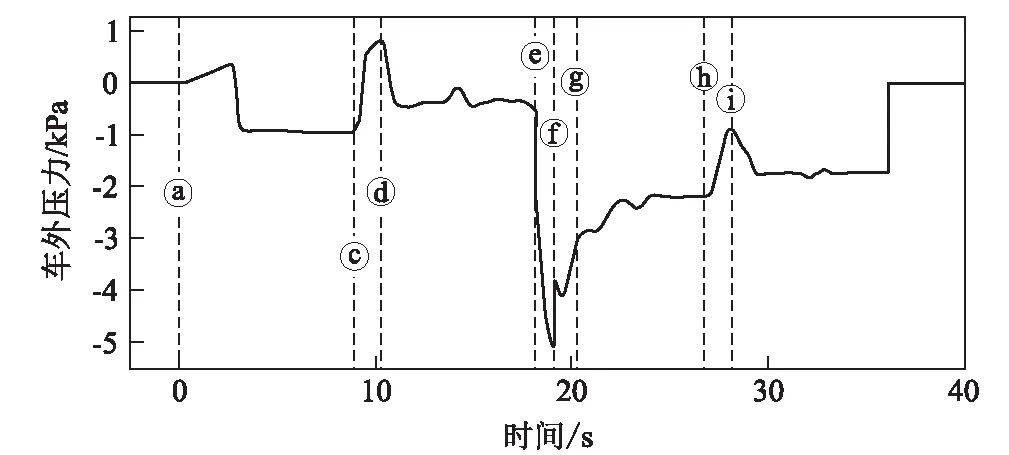
图4 观测列车头车车外压力时间历程曲线图

从图3、图4可以看出：

(1)观测列车头尾车和对向列车头尾车于ⓐ时刻和ⓑ时刻同时进入隧道，分别产生初始压缩波和膨胀波，对向列车进入隧道产生的两列压力波NC1和TE1以近似当地声速传播至隧道入口端后，转变成相反形式波形反射回隧道出口端，循环往复，观测列车车外压力同时受到自身和对向列车进入隧道产生的压力波影响，使得隧道内压力环境相比单列车通过隧道更为复杂。

(2)观测列车头车车外压力在ⓔ、ⓓ、ⓖ、ⓗ时刻分别受到压力波NC1、TE1、TC1、NC2和TE2的影响而发生剧烈变化。

(3)在ⓔ时刻，观测列车头车经过对向列车头车，加之两列膨胀波NE1和NE1’的同时影响，观测列车头车车外压力急剧下降；在ⓕ时刻，观测列车头车经过对向列车尾车，头车车外压力急剧上升。

2.2 隧道长度对车外压力的影响

单列车通过隧道和隧道中央等速交会情形下，列车以400 km/h通过不同隧道长度时，头、中、尾车的车外最大正压值、最大负压值和最大压力峰峰值的变化规律如图5、图6所示。

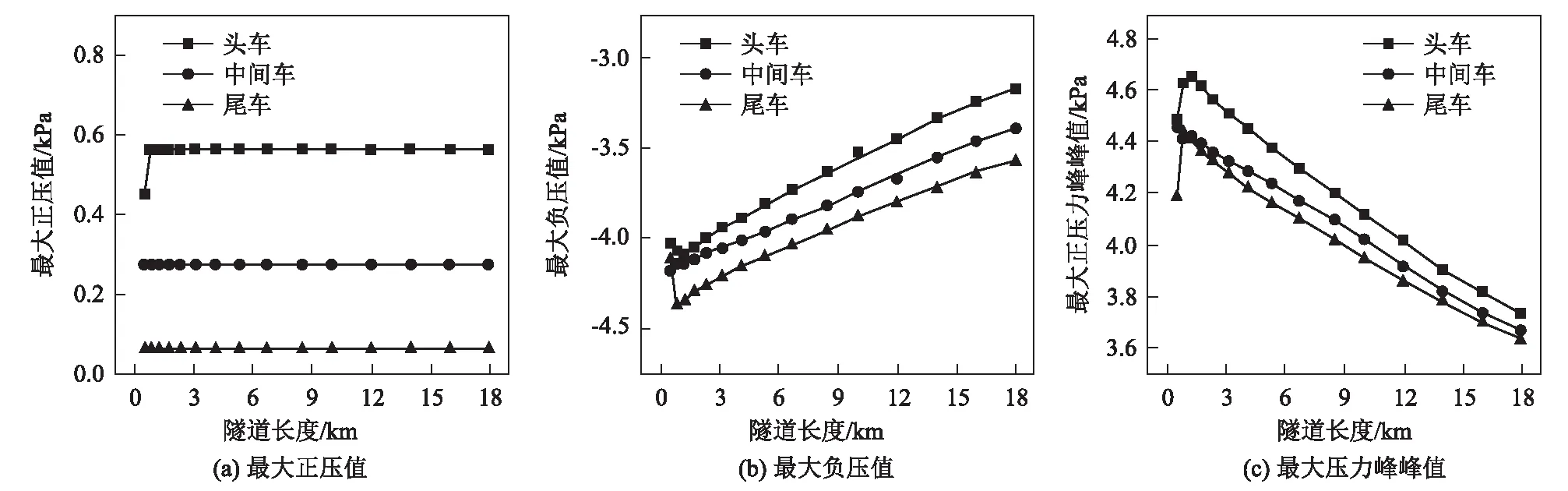
图5 单列车通过隧道情形下车外压力幅值随隧道长度的变化规律图

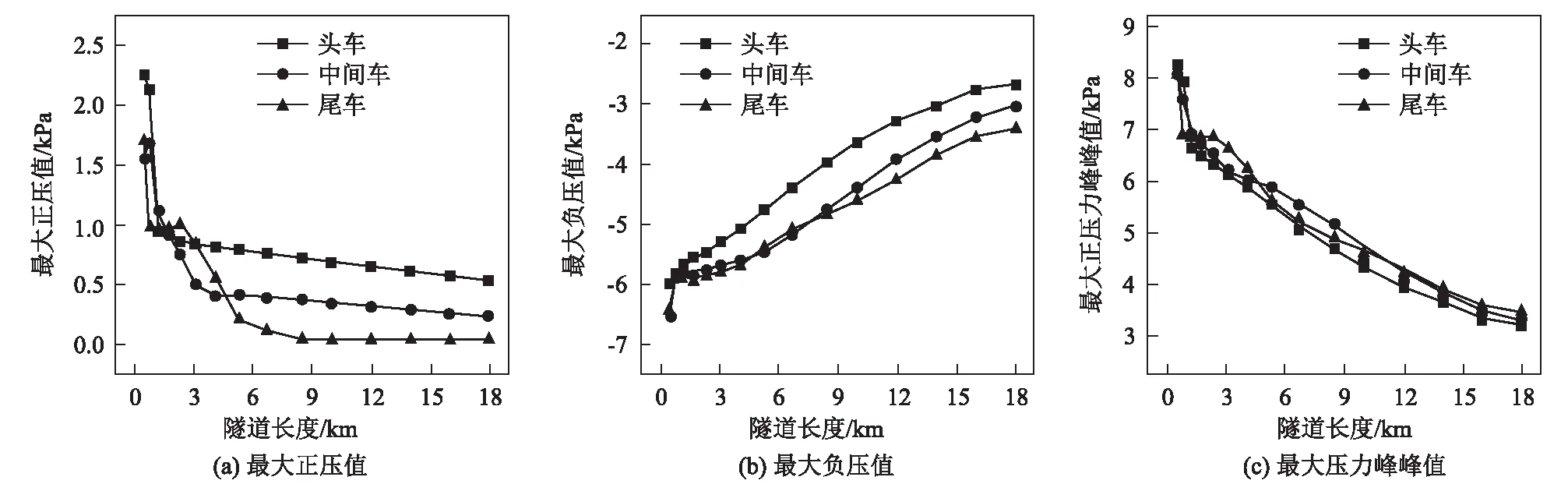
图6 隧道中央等速交会情形下车外压力幅值随隧道长度的变化规律图

从图5、图6可以看出：

(1)单列车通过隧道或隧道中央等速交会情形下，由头车到尾车，车外最大正压值和最大负压值总体上分别依次减小和增大，且最大负压值的绝对值远大于最大正压值的绝对值。

(2)单列车通过隧道情形下，隧道长度为500～800 m时，头车外最大正压值随隧道长度的增大而明显增大，隧道长度大于800 m时，头车外最大正压值随隧道长度增大基本保持不变；中间车和尾车的车外最大正压值则随隧道长度变化始终基本保持不变。

(3)单列车通过隧道情形下，隧道长度为500～1 200 m时，头、中、尾车的车外最大负压值和最大压力峰峰值随隧道长度的增大而明显增大；隧道长度为800 m或1 200 m时，头、中、尾车最大负压值和最大压力峰峰值最大；隧道长度大于1 200 m时，头、中、尾车的车外最大负压值和最大压力峰峰值则随隧道长度的增大而减小。

(4)隧道中央等速交会情形下，隧道长度为500～1 200 m时，头、中、尾车的车外最大正压值、最大负压值和最大压力峰峰值均随隧道长度的增大而明显减小；隧道长度为500 m或800 m时，头、中、尾车的车外最大正压值、最大负压值和最大压力峰峰值最大；隧道长度大于1 200 m时，头、中、尾车车外最大正压值、最大负压值和最大压力峰峰值随隧道长度的增加而减小，但减小的趋势有所减缓。

综上所述，单列车通过隧道和隧道中央等速交会情形下，车外压力最大正压值、最大负压值和最大压力峰峰值的最不利隧道长度范围均为500～800 m。

2.3 最不利隧道长度估算公式的合理性验证

基于单列车通过隧道和隧道中央等速交会的最不利隧道范围，采用一维流动模型，通过选取更小的隧道长度间隔来确定更加准确的最不利隧道长度，以验证现有最不利隧道长度估算公式的合理性。

参考文献[10]给出了单列车通过隧道和隧道中央等速交会情形下最不利隧道长度的计算方法及解析公式。当列车速度小于409 km/h时，最不利隧道长度的解析公式如式(4)～式(6)所示。

(1)单列车通过隧道

头车最大正压值：

(4)

尾车最大负压值：

(5)

(2)隧道中央等速交会

头车最大正压和尾车最大负压：

(6)

式中：c——当地声速；

L——长度；

MTR—列车马赫数，MTR=VTR/c；

下标“TR”——动车组；

“TU”——隧道。

单列车通过隧道和隧道中央等速交会情形下的一维流动模型求出的最不利隧道长度和解析法求出的最不利隧道长度如表3所示。

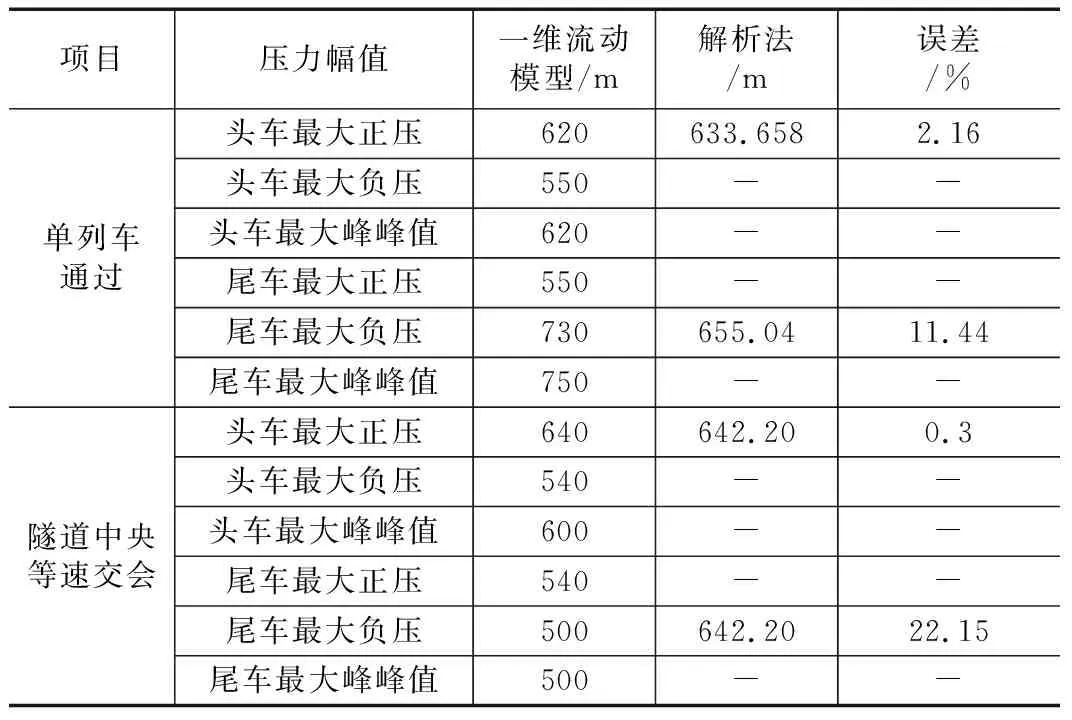
表3 最不利隧道长度比较表

从表3可以看出，单列车通过和隧道中央等速交会情形下，基于头车最大正压值的最不利隧道长度，一维流动模型和解析法的计算结果误差较小，均在3%以内；基于尾车最大负压值的最不利隧道长度，一维流动模型和解析法的计算结果误差偏大，误差为10%～20%，隧道长度为500 m和642 m时的尾车最大负压值误差仅在3%左右，可见500 m和642 m都可称为该情形下的最不利隧道长度，故可认为解析法计算结果较为合理。

2.4 隧道净空面积对车外压力的影响

不同隧道净空面积、8节编组(长210 m)列车在单列车通过隧道和隧道中央等速交会情形下以 400 km/h速度通过长 4 000 m隧道时，头、中、尾车的车外最大正压值、最大负压值和最大压力峰峰值的变化规律如图7、图8所示，计算参数如表4所示。以隧道净空面积每增大10 m2车外压力峰值变化的数值为绝对变化量，相对上一净空面积值变化的百分数为相对变化量。

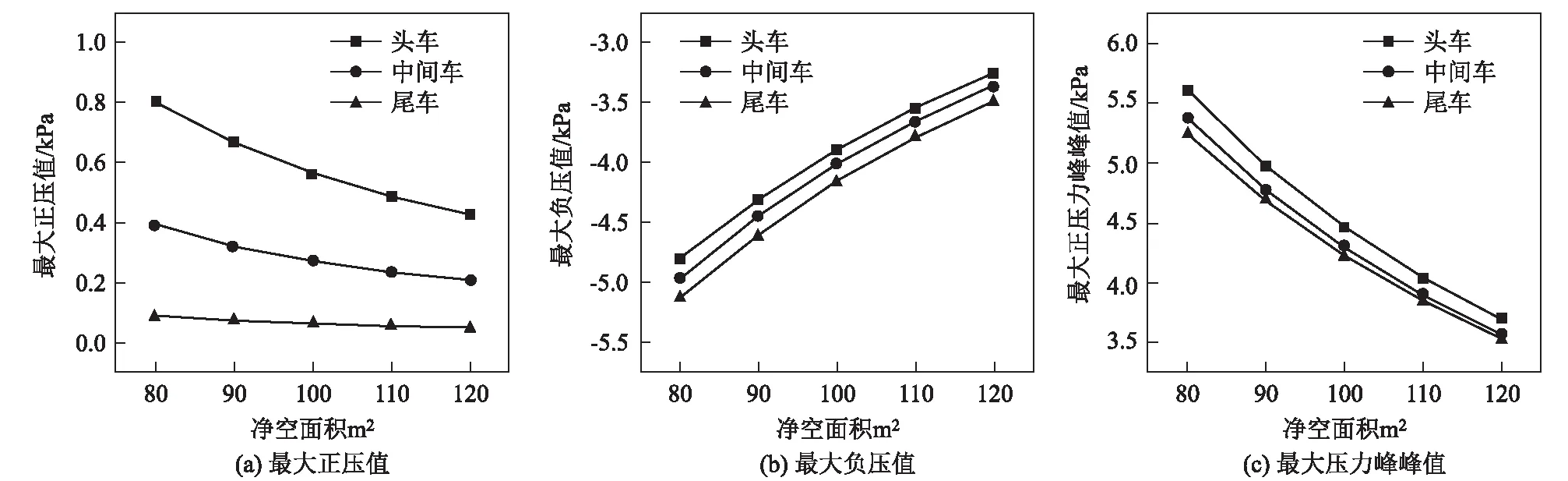
图7 单列车通过隧道情形下隧道净空面积对不同车厢车外压力幅值的影响图

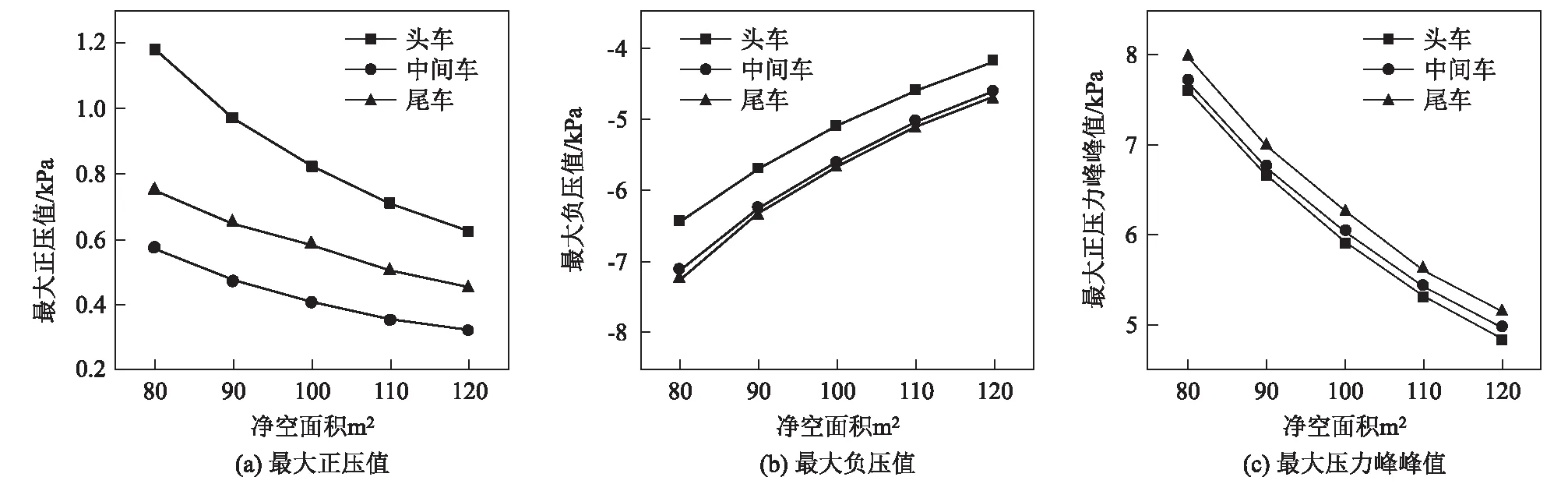
图8 隧道中央等速交会情形下隧道净空面积对不同车厢车外压力幅值的影响图

表4 不同隧道净空面积计算参数表

从图7、图8可以看出：

(1)单列车通过隧道和隧道中央等速交会情形下，车外最大正压、最大负压和最大压力峰峰值随隧道净空面积的增大而减小；隧道中央等速交会时，车外压

力峰值比单列车通过隧道时更大。

(2)隧道净空面积增大，车外最大负压值和最大压力峰值的绝对变化量远大于最大正压值的绝对变化量；隧道中央等速交会情形下，隧道净空面积增大，车外压力峰值的绝对变化量大于单列车通过隧道时。

(3)随着隧道净空面积的增大，车外最大正压值、最大负压值和最大压力峰值的变化量逐渐减小，可知净空面积较大时，车外压力峰值受到净空面积变化的影响较小。

(4)随着隧道净空面积的增大，单列车通过隧道时，不同车厢车外最大负压值和最大压力峰值相对变化量的平均值分别为9.33%和9.70%，车外最大正压值相对变化量的平均值为14.37%；隧道中央等速交会时，不同车厢车外最大负压值和最大压力峰值相对变化量的平均值分别为10.17%和10.52%，车外最大正压值相对变化量为13.37%；由此可知，车外最大正压值受隧道净空面积变化的影响大于车外最大负压值和最大压力峰值；隧道中央等速交会情形下，车外最大负压值和最大压力峰值受净空面积增大的影响略大于单列车通过隧道的情形，车外最大正压值受净空面积增大的影响略小于单列车通过隧道的情形。

3 结论

本文采用一维可压缩非定常不等熵流动模型和特征线方法研究了隧道长度和隧道净空面积对 400 km/h动车组车体压力载荷的影响特征，得出以下主要结论：

(1)列车通过隧道时，头车和尾车进入隧道产生的压缩波和膨胀波在隧道内以当地声速传播并反射，往复交替，形成了隧道内复杂的压力环境，引起了车外压力的剧烈变化；两列车隧道中央等速内交会时，车外的压力变化相比单列车通过隧道情形更加复杂。

(2)单列车通过隧道情形下，头车、中间车和尾车外最大压力幅值均随隧道长度的增大而先增大后减小，隧道长度为500～800 m时，车外最大压力幅值为最大值，可认为单列车通过隧道时的最不利隧道长度为500～800 m。

(3)隧道中央等速交会情形下，隧道长度为500～1 200 m时，头车、中间车和尾车外最大压力幅值随隧道长度增大而急剧减小；隧道长度大于1 200 m时，车外压力幅值的减小趋势变缓，隧道长度为500～800 m时，车外压力幅值为最大值，可认为隧道中央等速交会时的最不利隧道长度为500～800 m。

(4)选取更小隧道长度间隔进一步计算，并将一维流动模型和解析法计算的最不利隧道长度结果进行比较后发现，总体上，单列车通过隧道得出的最不利隧道长度较隧道中央等速交会得出的最不利隧道长度大；基于头车最大正压值的最不利隧道长度，一维流动模型结果和解析式计算结果的误差较小，基于尾车最大负压值的最不利隧道长度，一维流动模型结果和解析式计算结果的误差较大，但车外压力幅值误差仅3%左右，故可认为最不利隧道长度估算公式合理。

(5)车外压力幅值随隧道净空面积的增大而减小，车外压力负压值随隧道净空面积增大的绝对变化量远大于最大正压值的绝对变化量，净空面积较大时，车外压力幅值受到净空面积变化的影响更小。

(6)随隧道净空面积的增大，车外最大正压值增大的百分比为14%左右，车外最大负压值和车外最大压力峰值增大10%左右，故车外最大正压值受隧道净空面积增大的影响更大。