创设情境 搭建台阶 促进深度学习——以应用动能定理解决多过程运动问题为例

赖世锵

（广东仲元中学，广东 广州 511400）

动能与动能定理是高中物理机械能这一章的重点，也是力学的重点，高考的常考点.对于初学者来说，分析物体的受力情况与运动情况，应用动能定理求解多过程运动问题，往往存在一定的困难.在物体多过程运动过程中，往往存在着多个子过程，选择某一过程、多个过程还是选择全过程进行分析，这些都是学生比较纠结的，难以选择.如果能选择合适的过程，列出动能定理，可以事半功倍，反之，如果选择的过程比较繁琐，给解题带来很大的困难，在考场上就事倍功半，收不到好的效果.

如何搭建台阶，给学生带来学习的喜悦，这是教师的教学任务.深度学习理论指出在教师引导下，学生积极主动地参与教学活动，[1]往往围绕着某一挑战性的主题开展学习，基于问题解决的应用性和迁移性的学习方式，形成积极的情感、态度与价值观.[2]深度学习区别于浅层学习的一种学习方式，但是两者不相斥，是统一的.深度学习不仅关注学生获取知识，同时关注培养学生的模型建构能力、分析理解与综合应用的能力，更关注培养学生的高阶思维.为此，笔者通过创设情境，搭建台阶，通过变式练习，以实现一题多解，一题多变，由浅入深，循序渐进，[3]引导学生开展进阶式教学，促进学生深度学习，培养学生模型建构的科学思维，引导学生开展探究活动，掌握必备知识与关键能力.[4]

1 创设情境，巧选规律

情境呈现.质量m=10 kg的物体静止在水平桌面上，它与桌面之间的动摩擦因数为μ=0.2，物体在水平恒力为F=30 N作用下开始运动，发生位移为2 m时撤去该恒力，问物体还能运动多远？

分析：本题属于物体多过程直线运动问题，分两个阶段，即撤去水平恒力之前与撤去水平恒力之后两阶段均作匀变速直线运动.以物体为研究对象，画出受力分析与运动分析草图，如图1所示.可应用牛顿第二定律与运动学公式、分过程列动能定理与全过程列动能定理等三种方法解题.

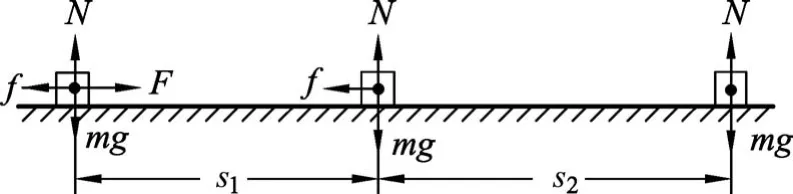
图1

解法1：运用牛顿运动定律和运动学公式求解.撤去水平恒力前，对物体，由牛顿第二定律得F-μmg=ma1，由运动学公式得v12=2a1s1，联立解得v1=2 m／s.撤去水平恒力后，对物体，由牛顿第二定律得μmg=ma2，由运动学公式得v12=2a2s2，联立解得s2=1 m.

解法2：分过程列动能定理求解.可将物体运动分成撤去水平恒力前与撤去后两个阶段进行分析，对物体，从开始到撤去水平恒力前的过程中，由动能定理得，从撤去水平恒力后到停下来的过程中，由动能定理得，联立解得s2=1 m.

解法3：全过程列动能定理求解，可将物体运动的全过程看作一个研究过程进行研究.对物体的运动全过程，由动能定理得Fs1-μmg（s1+s2）=0-0，代入数据解得s2=1 m.

点评：本题情境来源于生活实际，物体的运动分成两个阶段，即撤去恒力前与撤去恒力后两个过程，考查学生的模型建构与科学推理的科学思维.解决本题的方法很多，可以运用运动学公式、动能定理、功能关系等，显然对全过程列动能定理是最简洁、高效的，体现动能定理的优越性.在实际教学中，教师可以进一步引导学生总结优先使用动能定理的情况，即若物理过程中不涉及加速度、时间的时候或者有多个物理过程且不需要研究整个过程中的中间状态的时候都可以优先考虑动能定理.同时，教师总结应用动能定理的解题技巧.首先，建立模型建构，选择一个、几个或全过程进行研究；注意关注过程与过程的连接状态的受力情况与运动情况的变化；分过程或全过程进行研究，列出动能定理方程.

2 变式训练，熟悉规律

变式1.条件同上，当发生位移为s1=2 m时撤去该恒力，此时物体恰好进入右侧顺时针转动的传送带，传送带的速度为v0=4 m／s，传送带高为h=2 m，与水平地面的夹角为α=30°，如图2所示，已知物体与传送带间的动摩擦因数求：（1）试分析物体在传送带上的运动情况；（2）物体从传送带底端运动至顶端的过程中，摩擦力所做的功.

图2

分析：本题属于物体多个直线多过程运动问题，由原来在水平桌面上的直线运动，变式为水平桌面上的直线运动与传送带上的运动.就需要利用牛顿第二定律与运动学公式分析物体的运动情况.

第1问中，可选取物体为研究对象，在传送带上受力分析，由牛顿第二定律得μ2mgcosαmgsinα=ma，得a=μ2gcosα-gsinα=2.5 m／s2.由运动学公式得v02-v12=2as，解得s=2.4 m＜4 m.由于μ2mgcosα＞mgsinα，说明物体先做匀加速直线运动，运动了2.4 m与传送带达到共同速度4 m／s后，做匀速直线运动.第2问中，对物体从传送带底端到顶端运动过程中，由动能定理得，变形后代入数据得

点评：本题情境来源于生活，将第2阶段的运动情境改成物体在传送带运动，考查多个直线运动问题与传送带模型，涉及3个不同的运动过程.若要分析物体在传送带上的运动情况，则必须运用牛顿运动定律与运动学公式去判断，培养学生模型建构与科学推理的科学思维.通过变式训练，学生掌握了利用动能定理求解多个直线运动问题的方法，可以选择一个、几个或全部子过程作为研究对象，特别注意重力的功取决于物体的初、末位置，与路径无关，而摩擦力的功等于力的大小与路程的乘积.[5]

变式2.如图3所示，质量m=10 kg的物体静止在高h=1.15 m的粗糙桌面上，物体与桌面之间的动摩擦因数μ=0.2.现对物体施加一水平推力F=30 N，物体产生位移l1=2 m时撤去推力，物体又滑动了l2=0.5 m后飞离桌面求物体落地速度.（g取10 m／s2）

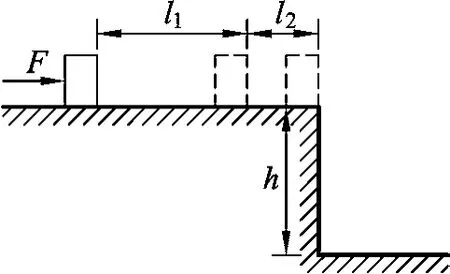
图3

分析：本题属于直线运动与曲线运动结合的多过程运动问题，由3个子过程组成，分别为有水平推力作用下的直线运动、撤去推力后的直线运动与平抛运动.

我是一个70后，从走进教师这个行业、担任班主任工作开始，负面情绪就始终存在。生活中的压力，工作中的烦恼，总是容易让人忧郁、焦躁、不安、易怒。既然不可避免地会与负面情绪相遇，与其逃避躲闪，不如正确面对、合理解决。听读与我随行，帮我减压、给我灵感，让我做回自己情绪的主人。

解法1：选取物体为研究对象，设撤去F时物体的速度v1，飞出桌面时物体的速度为v2，落地时物体的速度v3.全过程由3个子过程组成，即匀加速直线运动、匀减速直线运动和平抛运动.对每一过程，分别列动能定理得，联立以上各式解得v3=5 m／s.

点评：本题设计意图是让学生熟悉应用动能定律解决多过程运动的各种情境，包括直线运动与曲线运动等，考查学生模型建构能力与综合分析能力，锻炼学生科学思维能力.通过变式训练，学生熟悉了利用动能定理求解直线与曲线运动结合的多过程问题，知道了需要适当选取运动过程，列出相应的动能定理，并结合曲线运动知识求解.

变式3.条件同上，如图4所示，物体（可视为质点）离开桌面后，刚好经过圆弧上的M点，并沿着切线方向进入粗糙竖直圆弧轨道，NP为圆弧竖直直径，其中N为轨道的最低点，P为最高点，∠MNP=60°，轨道半径R=0.1 m.若桌面高度未知，不计空气阻力，g取10 m／s2.（1）求物体运动到M点时速度的大小；（2）若物体恰好能通过圆弧的最高点P，求在竖直轨道上摩擦力所做的功.

图4

分析：本题进一步一题多变，抛出后的物体做平抛运动，然后进入粗糙圆弧轨道，这里包括匀变速直线运动、平抛运动、圆周运动等4个运动过程.需要结合平抛运动的规律与动能定理求解，尤其是物体在圆周运动上运动时，需要应用动能定理求变力的功.

第1问中，对物体，在M点，由平抛运动规律得.第2问中，若物体恰好通过最高点P，在最高点P处，由牛顿第二定律得.物体从M到P点的过程中，由动能定理得代入数据联立解得Wf=-20 J.

点评：本题将直线运动与曲线运动再次结合起来，创设“滑一滑”“抛一抛”“转一转”等物理情境，用能量观念来解决实际问题.考查了学生的模型建构、科学推理与科学论证的科学思维核心素养.[4]当求解M的速度时，由于不知道桌面与A点的高度差，无法应用动能定理求解物体运动到M点的速度，但借助平抛运动规律得知若能求出物体飞出桌面时的速度即可，于是应用动能定理求解飞出桌面的速度大小.

图5

分析：本题属于物体往复多过程运动问题，小物体先做匀加速直线运动，撤去外力后做匀减速直线运动，接着冲上斜面后返回，来回运动，最终停在某一位置.应优先考虑动能定理解题，此外，要计算时间间隔，则必须应用牛顿第二定律与运动学公式来求解.

第1问中，由于PQ为光滑斜面轨道，小物体冲上斜面后必定会原路返回，即小物体最终会停止在水平轨道NP上.对小物体的全过程，由动能定理得Fl1-μmgx=0-0，代入数据解得x=6.5 m.故小物体最终停止的位置距N点的距离d=x-2l=1.5 m.第2问中，对小物体，从N到P过程中，由动能定理得，解得vP=4 m／s.小物体在斜面上运动时，由牛顿第二定律得mgsinθ=ma，小物体从P点到最高点再返回到P点，由于斜面光滑，故上滑与下滑均做匀变速直线运动，于是有，联立解得 Δt=1.33 s.

点评：本题情境来源于滑雪、滑板或轮滑运动，从一侧运动到另一侧，不停地往复运动.考查学生的模型建构与科学推理的科学思维，分析与综合能力.若选取从N到P、斜面PQ上往返、从P到N、斜面MN上往返，接着从N到P运动，从而判断到某点停下，显然，这样十分繁琐.若选取全过程，则很简便，应用动能定理只需关注物体的初、末状态而不需考虑运动过程的具体细节，对全过程列动能定理即可解决问题，充分体现了动能定理的优越性.在学习动能定理后，学生在解题时优先考虑动能定理，但是实在不符合，如像本题需要求解时间等，则必须借助牛顿第二定律与运动学公式.在教学中，教师可以根据情境设置递进式变式训练，让学生在训练中掌握必备的知识与关键能力，适当开展深度教学，培养学生的高阶思维能力.

3 小结

本文以应用动能定理解决多过程运动问题为例，通过创设物理情境，一题多解，一题多变，巧妙地给予学生搭建台阶，让学生形成必备知识与关键能力，开展深度教学，培养学生高阶思维能力.