智能车辆多信号灯路口快速节能车速规划*
2021-11-04冷江昊
冷江昊,孙 超,卢 兵
(北京理工大学,电动车辆国家工程实验室,北京100081)
前言
节能车速规划是指基于车辆的能耗模型合理规划出行驶过程中的车速,降低行驶的能耗。尤其是在城市工况下,车辆由于交通路口的红灯必须减速或停止,无意义的制动和怠速现象增加了能耗[1]。随着智能网联汽车技术的不断发展,V2X技术和具备自动驾驶功能的智能车辆已经逐渐涌现并迈向成熟,它们使得节能车速规划的部署更具现实性。在充满信号灯路口的城市中进行车速规划,需要结合交通信号灯信息,使得车辆通过信号灯路口时恰好处于绿灯相位。多信号灯路口节能车速规划能够有效降低车辆行驶过程的能耗,提升城市道路整体通行效率[2]。
近年来,众多学者对节能车速规划问题进行了广泛研究。Lim等[3]设计了一个基于路程的分层车速规划系统,包括上层的基于序列二次规划(SQP)的优化和下层的基于模型预测控制(MPC)的局部自适应。近似地,Huang等[4]使用遗传算法(GA)求解上层优化车速,局部自适应则采用内点法求解。Ozatay等[5]则使用动态规划(DP)在云端求解最优车速发送给目标车辆。上述研究没有考虑信号灯相位时刻(SPaT),难以适应城市内的多信号灯路口的实际路况。
在一些考虑多信号灯路口的研究中,道路限速和SPaT构成了节能优化问题的主要约束条件。Nguyen等[6]以CO2排放量构建代价函数,求解考虑SPaT的能耗优化问题。Huang等[7]使用SQP优化SPaT问题并用DP进行了最优性验证。Sunc等[8]考虑有效红灯时间,基于DP设计了一个鲁棒数据驱动的SPaT车速规划系统。Zhang[9]使用结合GA和DP的方法优化插电式混合动力巴士的全局参考车速。
由于SPaT约束的存在,多数学者采用DP或启发式搜索优化算法进行优化求解,造成了巨大的计算负担。上述方法虽然能够找到最优解,但难以达到实时应用,从而丧失了实车部署的潜力。对此,一些学者在降低车速规划问题的计算负担上进行了深入研究。De Nunzio等[1]提出了一种选取绿灯通行区间的方法,采用Dijkstra算法求解有向无环图。Guo等[10]使用广义残差最小算法求解信号灯约束最优车速。Homchaudhuri等[11]构建了一种基于fast⁃MPC的多信号灯通行车队燃油经济控制策略。Wu等[12]将SPaT问题转化为多阶段最优控制问题,并考虑了路口信号灯车辆等待队列的影响。然而,上述方法在追求计算实时性的同时一定程度上牺牲了能耗最优性。目前,兼顾能耗最优性和计算速度的节能车速规划方法依然处于探索阶段。
本文提出了一种考虑道路限速和信号灯相位时刻信息的快速节能车速规划方法,如图1所示。基于经济巡航车速分析,构建出基于能耗的有向无环图,应用DP对有向无环图进行求解,得到最优绿灯通行周期;进一步地,基于联立策略约束优化问题表达形式,将最优控制问题转化为非线性优化问题,采用内点法迭代求解;将DP求出的有向无环图最优解作为内点法优化迭代的初始解,进一步提高迭代收敛速度。
1 系统建模
本章介绍系统建模,包括车辆建模和信号灯相位时刻(SPaT)建模。
1.1 车辆建模
本文的目标车辆为燃油车,其纵向动力学和油耗模型[11],[13]可以表示为

式中:Fu.el为总燃油消耗率;ḟcruise为巡航燃油消耗率;ḟaccel为加速燃油消耗率;Fd为制动和怠速时的燃油消耗率;b0、b1、b2、b3、c0、c1和c2为能耗系数;a为车辆加速度;v为车辆速度;M为车辆质量;Cd为风阻系数;ρa为空气密度;Aν为车辆迎风面积;μ为滚动阻力系数;g为重力加速度;u为控制量,具体指车辆单位质量的驱动力或制动力;ζ为一个0-1变量,1代表制动或怠速,0代表其他情况;忽略道路坡度的影响因素。本文目标车辆的详细参数[11-13]如表1所示。
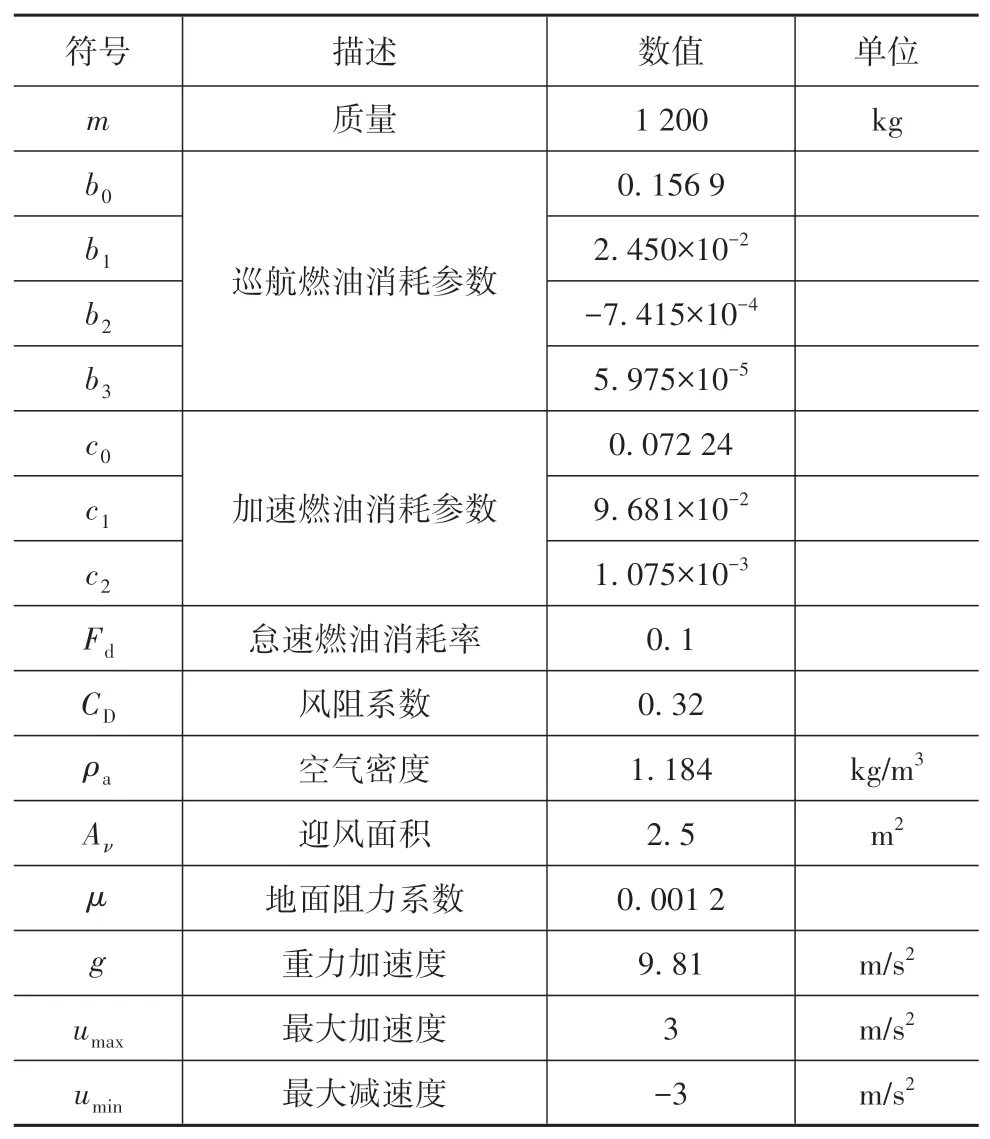
表1 目标车辆参数
1.2 信号灯相位时刻建模
一个信号灯周期分为红灯相位和绿灯相位,如图2所示。信号灯相位时刻的数学模型[1][8,11]可以表示为

图2 信号灯相位时刻模型
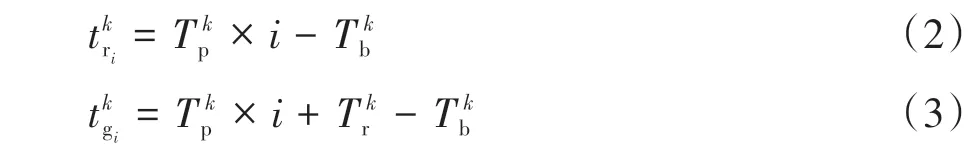
式中:k代表第k个信号灯路口;i代表第i个周期代表第k个信号灯路口的第i个周期的红灯开始时刻i代表第k个信号灯路口的第i个周期的绿灯开始时刻为第k个信号灯路口的周期时长为第k个信号灯路口每个周期的红灯时长为第k个信号灯路口的时间偏置。
2 快速节能车速规划
本章介绍快速节能车速规划方法,分为经济巡航车速分析、选取通行周期和非线性优化3部分。
2.1 经济巡航车速分析
在多信号灯车速规划问题中,智能车辆通过信号灯的周期数会对最终能耗产生较大影响[1]。为了求取通行周期,从全局的角度出发,假设车辆匀速通过各信号灯路口,忽略车辆起步和怠速消耗的能量,构建一个能耗与巡航车速的关系。

指定行程的到达时间为tarrive,则车辆的巡航车速vˉ可以表示为式中s代表整个行程的位移。在车辆匀速行驶时,驱动力和阻力相平衡,因此,单位质量的驱动力uˉ可以表示为

式(1)第1式的车辆油耗仅剩巡航项ḟcruise。

单位距离的油耗φ可以表示为

由式(7)可以看出,φ(vˉ)是一个仅与巡航车速vˉ相关的单变量函数(图3),φ(vˉ)为2.2节的基于能耗的有向无环图的构建提供了基础。
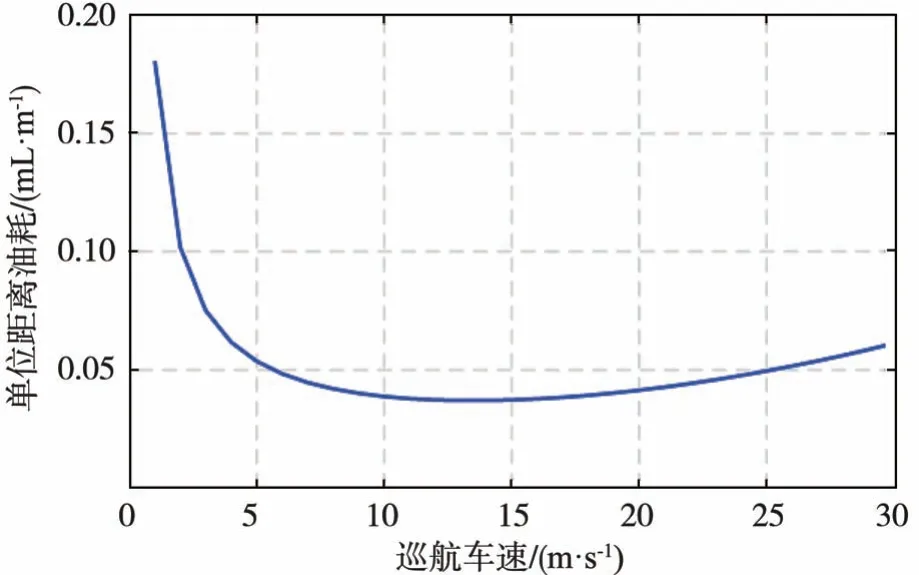
图3 车辆模型单位距离油耗φ与车速vˉ的关系
2.2 通行周期选取
本节基于式(7)构建出有向无环图,如图4所示,并采用DP求出该有向无环图的最优解。

图4 基于能耗的有向无环图建立过程
2.2.1 候选周期
假设车辆不考虑信号灯约束匀速行驶至终点,得到车辆通过每个信号灯路口的时刻tk(tk代表第k个信号灯路口的到达时间),在每个信号灯路口扩充3个离tk最近的周期P1、P2、P3。
2.2.2 候选时刻点
针对每个信号灯路口,在每个候选周期P1、P2、P3内分别采样n个均匀分布的候选时刻点,假定车辆匀速巡航行驶,基于式(7)构建出一个有向无环图,每条边的代价与巡航过程产生的能耗有关。

式中Jkm代表第k-1个和第k个信号灯路口的第m条边的代价。若vˉkm违反了限速约束,则其对应的边将会成为不可行边,与之对应的Jkm将会设置为+∞。
2.2.3 动态规划求解
采用DP对有向无环图进行求解,针对第k个信号灯路口,得到其最优通行时刻点m*k所在的周期,以及每两个信号灯路口之间的巡航车速vˉk*。
2.3 非线性优化
本节将多信号灯路口的节能最优控制问题转化为基于N个离散网格点的非线性优化问题。
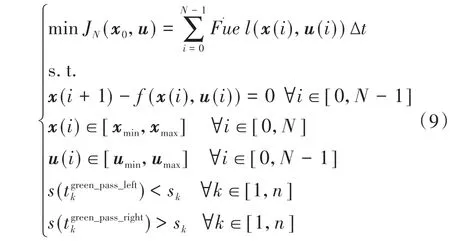
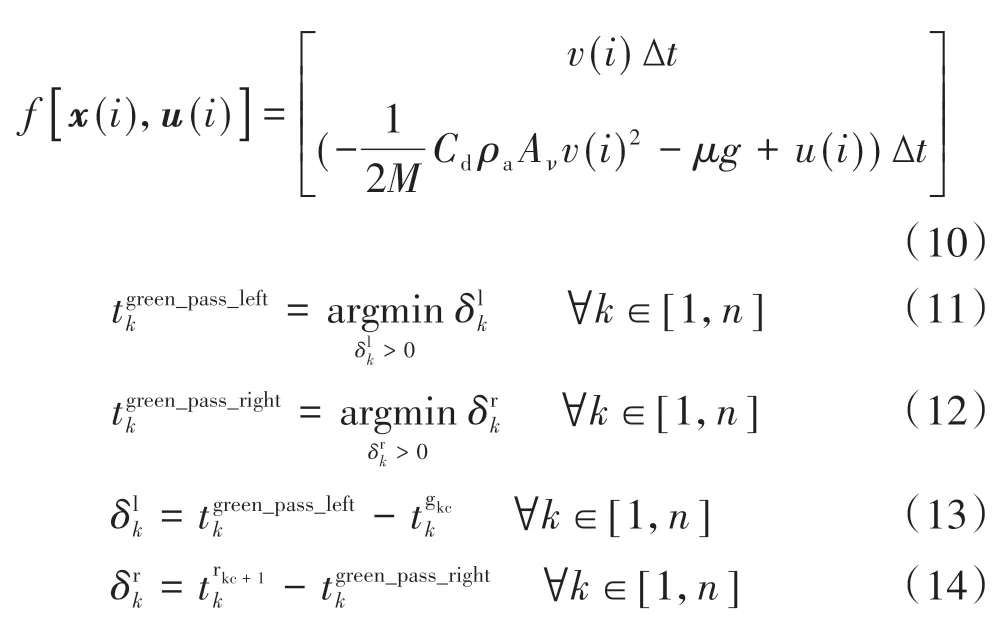
式中:xmin和xmax分别代表状态变量的下限和上限,xmin=[0,0]T,xmax=[smax,vmax(s)]T;smax为整段行程的位移;vmax为道路限速;umin和umax分别为控制量的下限和上限。此外,还必须满足2.2节求出的信号灯相位时刻约束分别代表第k个信号灯路口的第kc个周期下的绿灯开始时刻和第k个信号灯路口的第(kc+1)个周期下的红灯开始时刻分别为绿灯开始时刻与离散点之间的距离、红灯开始时刻与离散点之间的距离分别代表离绿灯开始时刻最近的离散点、离红灯开始时刻最近的离散点。上述约束保证了车辆到达第k个信号灯路口的时刻位于第kc个周期的绿灯相位范围内。
2.2节DP求出的有向无环图的最优解已经接近非线性优化的最优解。因此,将DP所得的有向无环图的最优解直接作为内点法优化过程的初始迭代值,提升收敛速度。
3 仿真验证
3.1 改进的智能驾驶员模型(MIDM)
本文中使用改进的智能驾驶员模型(MIDM)[8]作为基准,与本文提出的方法进行对比。智能驾驶员模型(IDM)是一种跟随前车的模型,基于前车的距离计算自车的加速度[8]。与IDM相比,MIDM将前车替换为信号灯路口,MIDM可以表示为

式中:dsf为当前位置与下一个信号灯路口的距离;alimit代表最大加速度,本文设为3 m/s;vlimit为一个小于道路限速的车速上限;dpreview代表驾驶员前视距离,本文设为100 m。
3.2 仿真场景构建
本文中构建了一个包含多个信号灯路口的仿真场景,信号灯路口的SPaT信息和各段道路的限速信息如表2所示。仿真环境为Matlab2019b,CPU Intel i7⁃8750H,RAM 16GB。

表2 仿真场景
3.3 方法对比验证
将本文提出的方法的平均车速设置为6、7、8、9和10 m/s。图5展示了依照2.2节方法DP所求的有向无环图的最优解,每个信号灯路口的每个候选周期内采样5个候选时刻点,从中可以看出,DP选取了合适的通行周期。基于DP求解有向无环图的计算时间为微秒级,与后续非线性优化相比可以忽略。
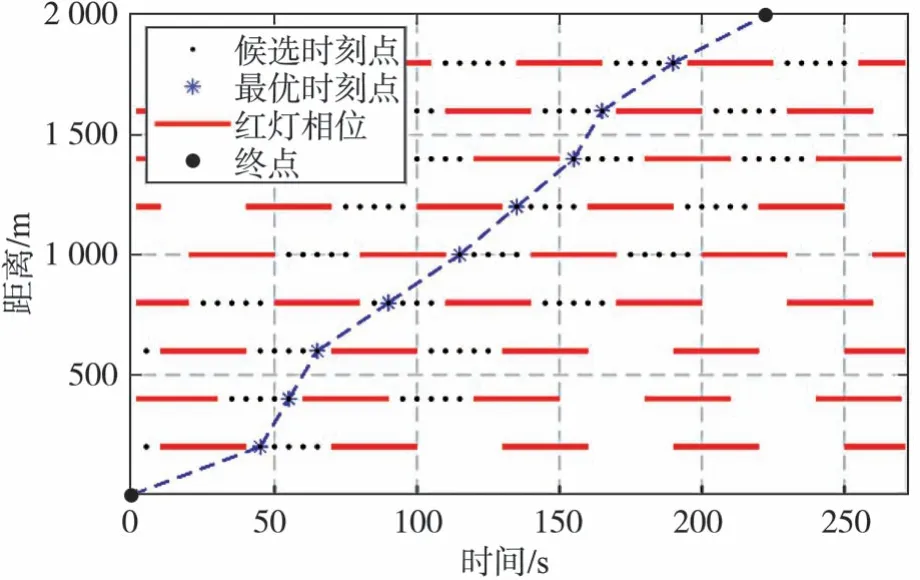
图5 基于能耗的有向无环图求解(平均车速9 m/s)
在得到车辆通过每个信号灯路口的最优通行周期后,基于2.3节将最优控制问题转化为非线性优化问题,网格间距设定为5 m。使用OpenOCL[14]进行求解,OpenOCL是一个基于Ipopt优化求解器[15]和CasADi自动差分框架[16]的算法库。其中,Ipopt基于内点法求解大规模非线性优化问题。此外,将DP求得的有向无环图的解作为非线性优化的初始解。
图6 展示了本文方法在平均车速9 m/s下的仿真结果。从中可以看出,DP求得的有向无环图的解非常接近最优解。将DP求得的有向无环图的解作为优化迭代的初始解,加速了内点法优化的迭代收敛过程。此外,与最大车速16.67 m/s的MIDM相比,本文提出的方法具备一个更加全局的视角,防止车辆在到达信号灯路口时处于红灯相位,从而避免了车辆在信号灯路口的停车和减速;而MIDM虽然到达时间与本文方法相近,但速度曲线更激进,出现了在信号灯路口停车等待的现象,不利于能耗降低。
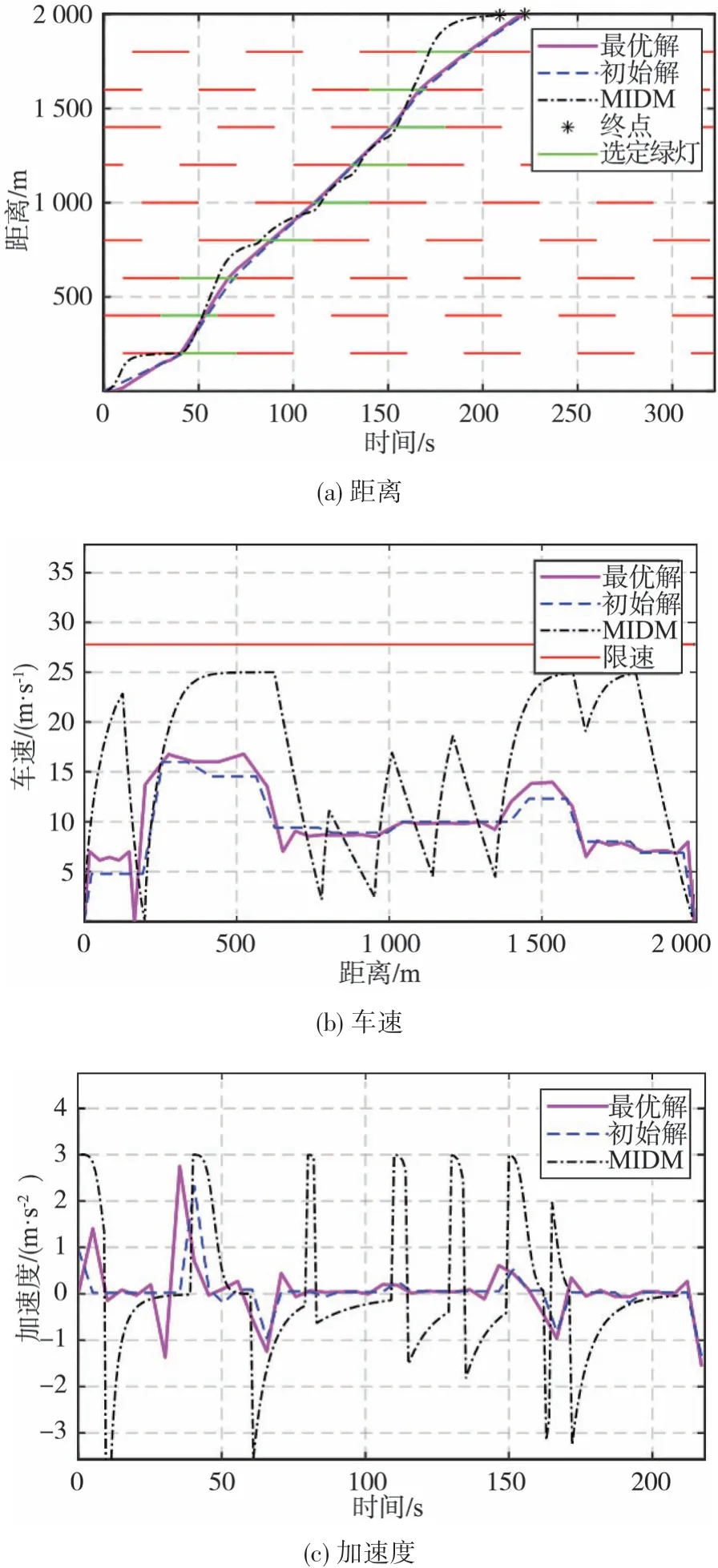
图6 非线性优化和MIDM的位移、车速与加速度(平均车速9 m/s,MIDM最大车速16.67 m/s)
仿真验证的关键评价指标有两项,即能耗和计算时间,其中能耗由1.1节车辆建模的油耗模型进行计算。表3、表4和图7给出了仿真验证的结果。与MIDM相比,本文提出的方法降低能耗30%以上,同时保持了高实时性的计算速度。此外,将DP求出的有向无环图最优解作为内点法优化的初始解,加快了收敛速度。与OpenOCL自带的基于规则的迭代初始值生成方法[14]相比,平均车速6、7、8、9和10 m/s的计算时间分别降低了50.41%、53.10%、52.93%、43.88%和55.66%。

图7 仿真结果对比

表3 油耗仿真结果

表4 计算时间仿真结果
4 结论
本文中提出了一种智能车辆多信号灯路口快速节能车速规划方法。基于巡航车速能耗分析,构建有向无环图,采用DP求解有向无环图,得到最优通行绿灯周期。进一步地,基于最优通行周期将最优控制问题转化为非线性优化问题,将DP求解的有向无环图的解直接作为内点法迭代的初始解,加快迭代收敛速度。仿真结果表明:(1)本文提出的方法较MIDM模型节能30%以上;(2)与基于规则的迭代初始值生成方法[14]相比,DP提供初始解提升了40%以上的计算速度。本文方法兼顾了节能效果和计算实时性要求,具备一定实时应用的潜力。
