LabVIEW软件设计的金字塔数独求解系统

三亚学院理工学院 缪克俊

三亚市第一中学 黄丽萍

三亚学院理工学院 汪 源 刘永旗

本文基于LabVIEW软件设计了一款求解9×9金字塔数独的系统。在对9×9金字塔数独解题规则分析的基础上，建立求解9×9金字塔数独的数学模型，在数学模型的基础上采用回溯排除算法设计一套求解金字塔数独的算法，并利用LabVIEW软件进行程序的设计，并得出9×9金字塔数独的求解结果。

数独起源于18世纪的瑞士，由著名数学家欧拉发明的拉丁方阵是数独前身，拉丁方阵中每一行和每一列都是由不重复的n个数字或者字母组成的，以拉丁方阵而变更出现在的数独，与现在的数独相比少了每一个宫不重复的规则。

标准9×9数独有6 670 903 752 021 072 936 960个组合，数独游戏难度的差异根据数独题目提示数量（N）以及提示数量（N）的摆放来决定的，每少一个提示数量（N），其出题难度会随之提高。根据权威机构认证，目前发现的最少提示数9×9标准数独为17个提示。并且在标准版数独以外，数学家们在数独本质不变的情况下，去对规则、表格进行变形创造出各种有趣的变形式数独，9×9金字塔数独就是其中一种，棋盘如图1所示。

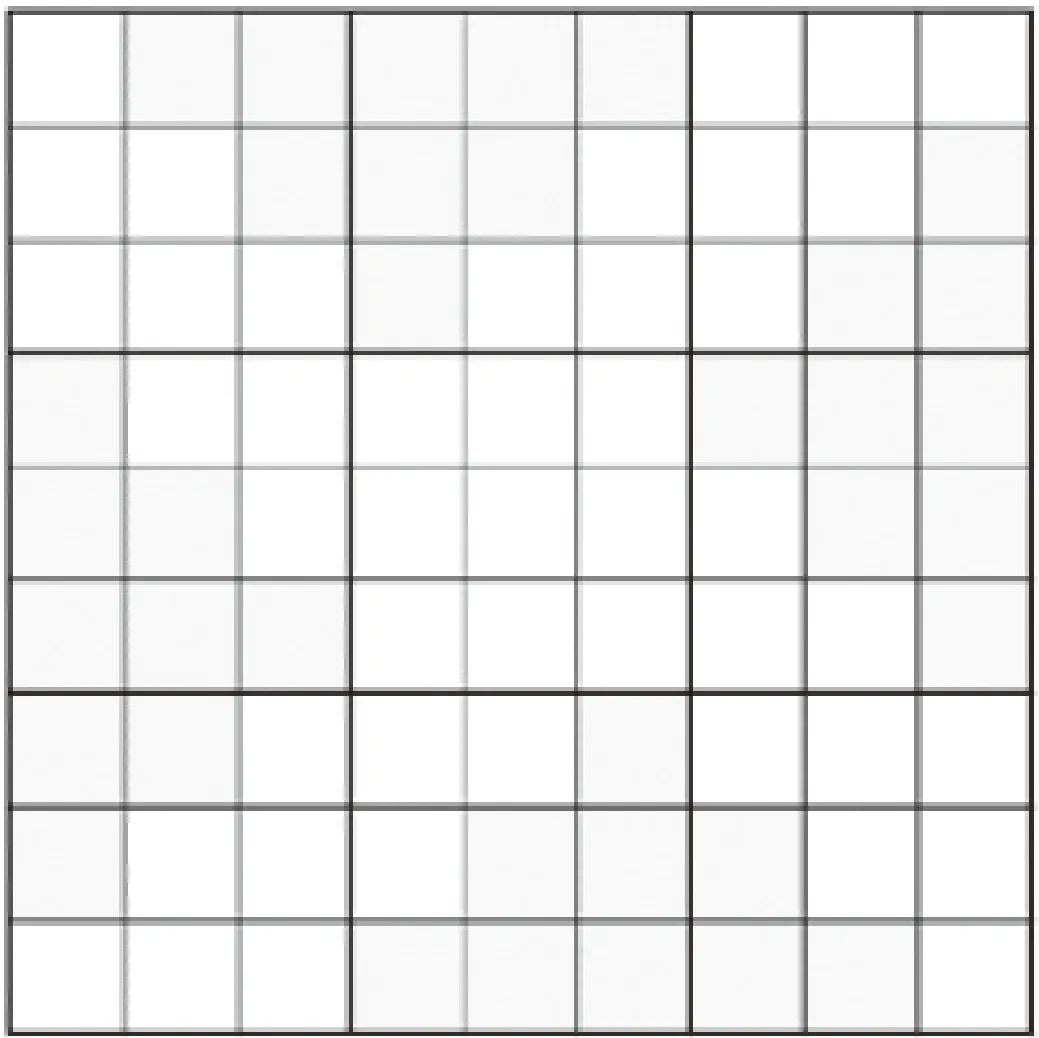
图1 9×9金字塔数独棋盘

本文利用图形化编程软件LabVIEW进行金字塔数独的求解，在金字塔数独解题规则分析的基础上，建立求解9×9金字塔数独的数学模型，在数学模型的基础上采用回溯排除算法设计一套求解金字塔数独的算法，并在LabVIEW软件中编程实现求解算法，让计算机自动进行9×9金字塔数独的求解。

1 设计方案

9×9金字塔数独棋盘如图1所示。其解题规则为：棋盘中每个3×3宫内填写1-9的自然数不重复；且棋盘中每一行填写1-9的自然数不重复；且棋盘中每一列填写1-9的自然数不重复；且棋盘中每个黄色金字塔区域（9个空）中填写1-9的自然数不重复。针对计算机快速运算的特点，本文采用回溯排除算法进行算法设计。

回溯排除法是一种搜索算法，其基本思路为：在一个问题中，根据题意给出的边界条件划定出所有可能解的范围，根据题意确定出约束条件。利用计算机程序顺次在所有可能解中利用约束条件进行排除不可能的解，搜索时按照深度搜索的方式进行。即在第1个需要填写的单元格[i,j](i,j=1,2,…,9)内选择满足约束条件的最小可能解Ai,j,1，然后以Ai,j,1为出发点，利用约束条件搜索第2个需要填写的单元格[k,l](k,l=1,2,…,9)的最小可能解Ak,l,2。如果搜索到Ak,l,2，则继续搜索第3个需要填写的单元格的最小可能解。如果第N个单元格没有满足约束条件的解，则返回第N-1个单元格，搜索比原最小可能解大且满足约束条件的最小可能解。依次类推，直到所有单元格的可能解都被找到，则得到了该问题的一个完整解。

对于9×9金字塔数独，约束条件包括“行排除”、“列排除”、“宫排除”和“金字塔排除”，其中“行排除”的具体条件是：当前搜索的单元格中可以填写的数字必须和该单元格所在行的其他8个单元格中已填的数字不重复。其他约束条件可以类似写出，不再赘述。其中需要强调的是，“金字塔排除”的约束条件只在搜索的单元格处于某个金字塔范围内时才使用。回溯排除法的算法流程图如图2所示。

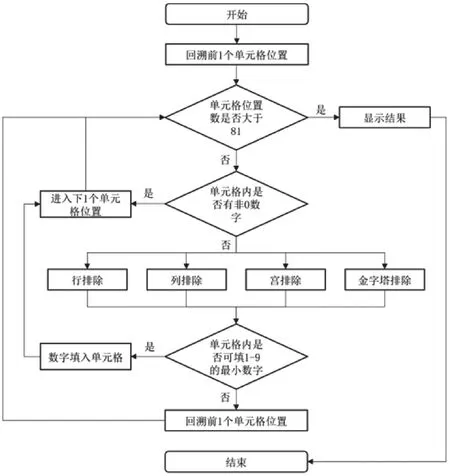
图2 回溯排除法设计流程图

2 LabVIEW程序设计

LabVIEW软件是通过数据流编程和图形化编程实现编程设计，数据流编程也被称为G语言，是一种数据流编程语言。通过导线连接不同功能的函数或节点，图形化的程序框图结构决定程序如何执行。LabVIEW的程序有三个组成部分：程序框图（Block Diagram）、前面板（Front Panel）和图标/连接器（Icon/Connector）。

标准数独表格一共拥有81个表格，从第1个单元格开始到最后1个单元格，需要将数独棋盘第1个单元格开始的每一个单元格内的数值进行识别，识别它是否为已填数字，已填用1表示，未填用0表示。若为1说明该单元格是有已填数字，执行“单元格+1”步骤，再进行下一单元格的判断；若为0说明该单元格是需要去填入数值的单元格，在该单元格使用“行排除法”、“列排除法”、“宫排除法”和“金字塔排除法”在整个数独内进行判断，来筛选可填入的1-9之间的最小数值。该单元格填入排除法筛选出可填入的最小数值，执行“单元格位置+1”步骤，再进行下一单元格的判断。若发生错误的情况，即该单元格无法填入1-9之间的任意数字时，可知该单元格的前序单元格中填入最小数字并不是这个数独的解，需要将往前推算，执行“单元格位置-1”步骤，并进行回溯来判断之前填入数字的正确性。依次类推，直到最后一个单元格可以填入1-9之间的某个数字，该结果即为该数独的解，但该解不一定是唯一解。

在LabVIEW程序中，数独由数组形式进行呈现，如图3所示。其中数组元素是“图片下拉列表”控件，控件中插入0-9的10张图片，索引数值分别为0-9的数字。其中9个红色线划分的区域即为9个宫，4个黄色线划分的区域即为4个金字塔。

图3 前面板中的数独

根据LabVIEW设计算法流程图可知，一个标准数独表格一共拥有81个单元格，以单元格位置小于81为条件建立求解是否完成的判断条件，单元格位置小于81即该数独还未破解；当单元格位置大于等于81时，即该单元格已经通过推算将81个单元格填入解题对应数字，数独求解过程完成，显示数独答案。

控件传输数据会从第0个单元格开始，因此对于每个单元格所需要去解析该单元格所在的行列进行分析。对单元格位置进行商与余数，公式如下：

在此基础上需要对未填入数字的单元格进行添加数字。初始状态下未填写数字的单元格内数字为0，先需要建立子VI来添加该单元格的数值，输入端为控件和行、列，输出端为控件，单元格所得到的行、列来确定该单元格位置，使用元素同址操作结构选定数独数组、数独数组单元格位置、该单元格的值。

根据该单元格所加的数值进行数独规则的判断，分别为“行排除法”、“列排除法”、“宫排除法”和“金字塔排除法”。下面以“宫排除法”为例进行说明。

宫排除法是需要选中该单元格所包含的宫（3×3）区域，因此先需要将控件所占的9x9区域调整为该单元格所包含的宫（3×3）区域。在行和列数值选择中，有着采集数独9个宫数据的区别，见表1所示。

表1 “宫排除法”单元格行列对应的宫

利用条件结构将行列所在的宫定义好宫第一个单元格，对单元格所对应宫进行数独数据采集，筛选出宫内没有出现的1-9之间的最小数，并结合“行排除法”、“列排除法”和“金字塔排除法”的结果，最终确定可以填入的最小数。

若一个单元格通过排除法所得1-9数值都无法填入，则是该单元格前面序列的单元格填入数值是错误的，需要以当前单元格位置往前推算，执行“单元格位置-1”步骤，并进行回溯来判断之前填入数字的正确性。依次类推，直到最后一个单元格可以填入1-9之间的某个数字。结果如图4所示。

图4 金字塔数独求解结果

在标准9×9数独求解的基础上，基于LabVIEW软件，设计一款求解9×9金字塔数独系统，达到求解数独的目的。在对9×9金字塔数独解题规则分析的基础上，利用回溯排除法进行了求解金字塔数独的算法设计，在设计算法的基础上利用LabVIEW软件进行程序的设计，通过对单元格进行“行排除法”、“列排除法”、“宫排除法”和“金字塔排除法”的判断，最终得出9×9金字塔数独的求解结果。