装配误差及交变温度对航天轴承套圈影响分析*
2021-11-03王兴东王郢瑞
王兴东,王郢瑞,唐 伟,高 鹏,汪 龙
(1. 武汉科技大学冶金装备及其控制教育部重点实验室,武汉 430081;2. 中国航天科技集团公司北京卫星制造厂,北京 100080)
0 引言
航天轴承是支撑机械臂运动的重要“关节”,在失重环境下其运转灵活性直接影响到动力传递的准确性以及系统工作的稳定性[1]。航天轴承实际装配中,由于薄壁壳体存在形位和尺寸等误差、轴孔装配轴线不重合的误差等,将导致装配体在装配完成后产生局部应力和变形。机械臂进入空间环境后,交变温度加重影响了配合件的配合精度和配合关系[2]。因此,研究装配完成的轴承装配体在空间环境等影响因素下的变形及应力,对于空间机械臂在轨寿命、精度、可靠性具有重要意义。
文献[3]在Hertz接触理论的基础上建立了考虑滚子尺寸误差与轴承内外圈滚道接触变形的计算公式;文献[4]对轴承的不规则几何尺寸模型的静态特性进行了分析,提出了一种基于轴承几何矢量描述的计算方法,却对于装配过程中的位姿误差影响鲜有描述;文献[5]分析了实心与空心圆柱滚子轴承接触变形,计算了其外部径向载荷、转速及空心率对轴承整体弹性变形的影响;文献[6]分析了单个滚子直径误差对滚子最大载荷和承载滚子数量的影响。以上学者用弹性力学及Hertz接触理论对带有几何误差的轴承进行了接触力、接触变形及轴承寿命分析,并通过有限元软件求解了载荷分布规律。对于轴承尺寸较大,变形量大,且制造装配过程中误差对的轴承圈道和游隙的影响研究较少。
文献[7]针对环境因素对航天机构可靠性的影响,提出了结构设计和材料选择建议以提高可靠性。文献[8]通过热学和变形协调关系分析了交变温度影响航天轴承过盈量和预紧力的规律。文献[9]针对空间机构工作环境工况下建立了轴承工作时的内部接触载荷与间隙数学模型,求解了全轴系的应力与变形解。文献[10]分析了温度变化对装配过盈或间隙量的影响,推导了预紧力和轴承游隙的关系。
上述文献对轴承装配误差及变形、交变环境轴系载荷和摩擦力矩变化进行了研究,但尚未建立同时考虑尺寸和装配误差的交变温度计算模型。为此建立同时考虑轴承装配位姿误差和交变温度的轴承游隙计算模型,分析装配形位误差在交变温度环境下对角接触球轴承游隙及性能的影响。
1 形位误差装配理论分析
空间精密轴系由输出轴、一对角接触球轴承、关节壳体、输出端轴承压板、输出轴承内环轴套等组成,图1为某空间机械臂关节模块,轴承与输出轴通常采用过盈配合,压装力始终恒定且平行于轴承座孔轴线,由于航空用轴承尺寸较大,且壁厚较薄,压装过程中,会使轴承内圈膨胀变形。轴承中轴线与输出轴的轴线不重合会导致在强制压装过程中轴线倾斜接触面应力过大的情况;由于圆筒的装配问题可简化为壁厚圆筒弹性范围内的平面应力解,在过盈联接时其轴向应力为0,轴向力只有恒定不变的压装力。为此可将过盈配合与同轴误差产生的应力-应变叠加求解。
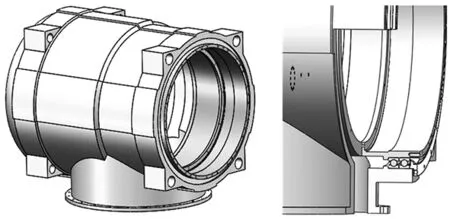
图1 三维模型
1.1 装配误差的影响
以内圈-输出轴为例,对于同轴误差的示意图如图2所示,倾斜接触面轴承内环和相应位置的滚动体接接触应力集中,造成局部变形过大引起轴承滚动体和运动套圈不规则转动,在较短的时间就会出现过度磨损,引起轴承过早疲劳损坏。可对其进行受力分析,如图3所示,压装力恒定不变为F的情况下,当轴线偏角为θ时,在结合面S处所受到的正压力可由结合面积S和摩擦系数f得出:
F轴=F压×cosθ
(1)
F=p×f×s
(2)
结合面所受的压力为:
(3)
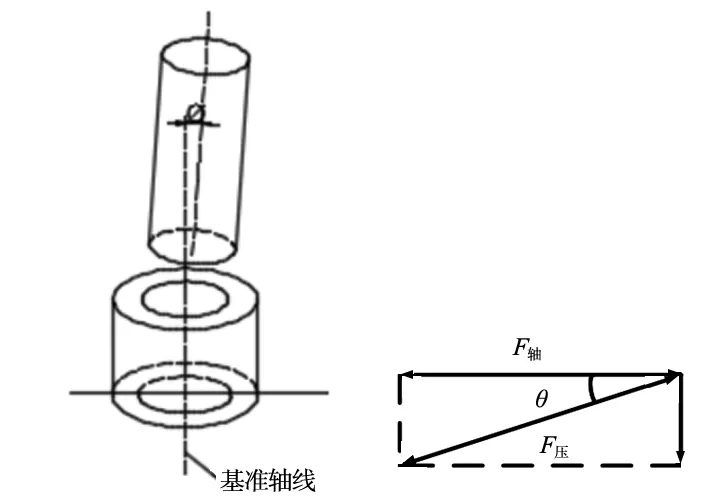
图2 同轴误差装配 图3 结合面受力分析
由上述分析可知,当作为配合件的输出轴固定时,轴承通过图4恒定的压装力装配时,同轴误差的影响可简化为偏移侧结合面压力增大的情况,通过求解增大的压力,可导致轴承内圈由于形位误差产生的额外应力与变形u,并叠加在过盈配合产生的变形中。
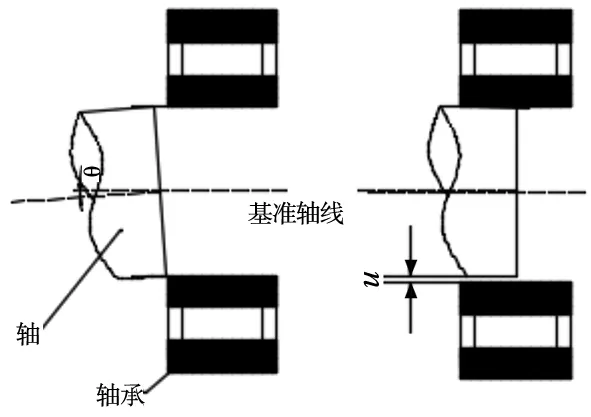
图4 误差装配图
1.2 过盈装配的计算分析
由于航天轴承及其配合件材料的弱刚性特性,在弹性范围内联接时会产生变形,存在同轴误差强制压装会导致一侧有较大的变形和应力,由弹性力学[12]圆筒的变形对于轴线的对称性,圆筒上任何一层均作圆形扩张,且筒上的任何一点也只会发生径向位移,而且等半径圆周上各点的位移相同,图5为作用于半径r处的单位长度单元体上的应力和应变。径向应力沿单元体的厚度dr由σ增加到σr+dr[13]。可得任意半径处径向应力表达式:
(4)
其中,P1为受到的内压,P2为受到的外压,r1r2分别为圆筒的内径和外径。
对于静力压装的轴承内圈而言,其只受来自输出轴的内压P轴,外压P2为0,将此边界条件带入式(4)中得此时由外压引起的径向应力为:
(5)
由内压产生的位移为:
(6)
式中,E为材料的弹性模量,μ为泊松比。
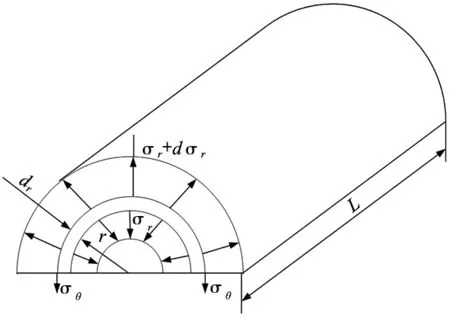
图5 单元体上的应力
1.3 交变温度对轴承的影响
在地面装配调试完成后,此时轴承内部的游隙为工作游隙,当工作游隙为微负值时,轴承的疲劳寿命最长但随着负游隙的增大疲劳寿命同显著下降。因此,选择轴承的游隙时,一般使工作游隙为零或略为正为宜。进入太空工作环境后,在交变温度作用下,主轴和轴承都产生相应的热变形。由于各组件材料不同,导致轴承配合处的过盈量变化,过盈量变化引起轴承结构参数的改变,影响航天轴承的传动精度和正常工作。
设交变温度的变化量为ΔT,首先在轴承内圈与输出轴配合处产生线性膨胀,热变形量Δds,ΔDi分别为:
Δds=αsdsΔT
(7)
ΔDi=αbDiΔT
(8)
由于变形处公称直径相等,由变形协调关系可知,由交变温度导致过盈量的变化ΔIi为:
ΔIi=(αs-αb)bΔT
(9)
进入深空环境后轴承内圈的变形总量Δu为:
Δu1=ΔIi+u
(10)
同理可得轴承外圈的总变形,因此轴承内外圈联立对轴承径向游隙的变化为:
Δu=Δu2-Δu1
(11)
2 装配体轴承刚度变化
2.1 装配引起的刚度变化
轴承刚度会直接影响到轴承对机械运转的效率。根据轴承受力与位移的关系,可得到其刚度[14]。
K=F/(δ1+δ2)
(12)
设轴承的工作游隙为u,其径向弹性位移为:
δ2=βδ0-u/2
(13)
式中,F为径向载荷,β为弹性变形系数,δ0为游隙为0时的弹性位移,δ1为轴承的径向弹性变形,δ2为轴承内圈与轴的接触变形。
本文以图4中轴承内圈相对位移的方向,将过盈装配产生的径向力和变形作为转子对轴承的径向作用力和位移,对不同过盈配合量的轴承内圈倾斜角影响下的轴承径向刚度进行了计算。
结果见图6,Kθ=0和Kθ分别表示未倾斜的角度和倾斜时的刚度,由图6可知:随着倾斜角的增加,径向刚度随之线性增加,这是由于轴承倾斜装配导致径向压力增大,当过盈量发生改变时,过盈配合接触面应力改变,引起轴承径向刚度改变,随着过盈量的增加刚度比增加。
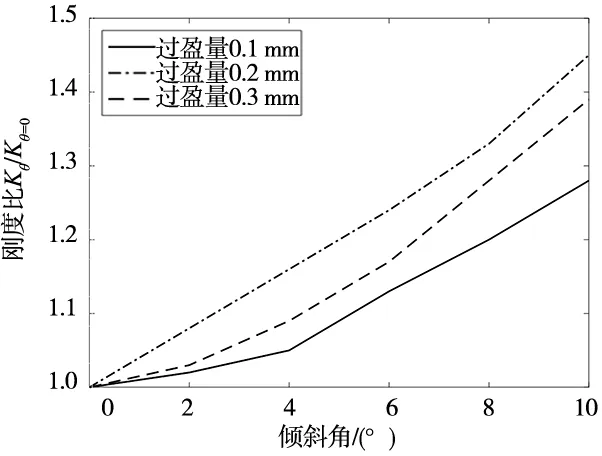
图6 倾斜角对刚度的影响
2.2 温度引起的刚度变化
为研究交变温度对装配完成后的轴-轴承的影响机理,以弹性力学、变形协调关系建立接触应力随交变温度变化的数学模型。在大幅交变温度环境中,精密轴系及相应的配合件发生热变形,温度应力和热膨胀变形均会影响轴承的刚度。
由于航天设备表面覆盖有热传递导管,因此将温度场设定为均匀温度场,无温度梯度。在完成装配后,由于协调变形条件,此时轴和轴承配合面应力相等。此时的温度应力为:
(14)
将温度函数带入式(10)可得温度产生的变形:
(15)
此时的式(12)中的F为温度应力σT,径向变形为温度产生的热变形ur。
随着温度的升高,轴承内圈的径向变形量增加,温度应力也线性增加,径向刚度上升幅度较少。温度应力对轴承刚度的影响不如过盈配合的大。
3 有限元验证
本文采用有限元方法对考虑形位误差的轴承-输出轴过盈安装等效应力及轴承径向变形量进行计算,以某空间机械臂关节角接触轴承为例,轴承内径为280 mm,外径为310 mm,轴承宽度为17 mm。为简化计算模型,忽略轴承保持架和滚动体结构的影响,把轴承简化成薄壁圆环,将数值分析计算的轴承内径的增量作为轴承径向游隙改变量,对装配完成的轴承-输出轴装配体施加交变温度场,模拟深空交变环境对轴承的影响。
3.1 模型的建立
模型的建采用SOLID185三维8节点单元类型,采用六面体单元进行实体划分,轴承内圈是重点分析的对象,将此部分的网格进行细化,划分结果如图7所示。由于轴承的内圈与输出轴的接触之间是一种接触非线性行为,需要对它们进行接触类型设置。考虑到过盈装配的摩擦行为,将接触类型设置为Frictional,对不同零件赋予材料,输出轴材料为TC4,轴承内圈材料为轴承钢材料,各材料参数如表1所示。根据轴-轴承的安装条件,对输出轴一端面固定约束,对轴承内圈施加第一个载荷步,绕其中心坐标系Z轴旋转一角度模拟形位误差,对轴承左端面施加一个位置载荷,模拟其压装的过程。

图7 输出轴装配模型 图8 模拟同轴摩擦

表1 各材料参数
3.2 装配分析
在理想装配时,轴承只受轴向的预紧载荷;在实际装配时,由于径向装配位置偏差即同轴误差引起径向偏载荷,强制压装开始时,轴线偏移侧接触应力明显增大,受载如图9所示,最大压力出现在轴线偏移侧轴承内圈内表面,也就是轴承的内沟道表面,最大等效应力为164 MPa,随着装配继续进行,内圈变形至输出轴与轴承轴线重合,此时的配合仅处产生间隙为1.53 mm。为研究不同角度的形位误差对装配体的应力影响,当角度发生改变时,最大等效应力随过盈量的增加而线性变化如表2所示,这意味在实体中,变形一侧的滚动体受压明显,会引起滚动体的轴线偏移,这也会引起滚动体与保持架圆周方向发生碰撞,加剧磨损和发热,容易导致保持架断裂。

图9 接触面压力 图10 接触面间隙

表2 不同倾斜角度下的压力与变形
3.3 交变温度场模拟
在装配完成后,为模拟太空交变温度的影响,对装配体施加一个随时间变化的温度函数,设定地面初始温度为22 ℃,在设备向阳面时,温度上升78 ℃~100 ℃,此时输出轴和轴承内圈配合面的等效应力和径向变形如图11所示。
在温度升高时,由于装配体不同组件之间材料不同,其热膨胀系数也不相同,导致在温度同时升高产生的热膨胀量也不相同,最大应力出现在轴线偏移侧为176.3 MPa,这是因为由于轴承内圈倾斜安装,导致局部变形,在温度应力的影响下应力增大;最大变形同样发生在轴线偏移侧为0.3 mm,内圈的变形增量对于轴承即轴承径向游隙的减少;在装配变形过后,温度升高,轴承内圈热膨胀大于输出轴,此时轴承和输出轴配合面产生间隙,装配失效,出现打滑甚至滚动体与内外沟道偏离的情况。

图11 温度升高的等效应力与变形
当设备背阳面时,温度下降72 ℃~-50 ℃,装配体各组件发生收缩,此时的轴承内圈收缩速度快于输出轴,最大等效应力如图12为222.9 MPa,轴承内圈的径向变形量为0.14 mm,即径向游隙的增加量;由于变形量的不同可导致安装变形处的收缩量不同,轴承内圈圆度出现误差,造成轴承传动时转动受阻,影响传动精度。

图12 温度降低的等效应力与变形
3.4 理想装配的温度场分析
为与带有形位误差的装配仿真进行比对,对轴承内圈-输出轴理想装配进行仿真,采用与之相同的安装过盈量以及材料参数,将轴承内圈与输出轴的轴线完全重合,进行压装模拟,施加-50 ℃~100 ℃的交变温度场,结果见图13。

图13 理想装配的温度场分析
可以看出,在温度升高时,带有形位误差的装配体比理想装配体等效应力多12.2 MPa,径向位移多0.19 mm;而在温度降低时,带有形位误差的装配体等效应力多71.5 MPa,径向位移少0.01 mm。
4 结论
(1)本文以某空间机械臂输出关节轴承端为研究对象,建立的装配模型可用来分析带有形位误差和交变温度下的径向游隙变化现象,该模型的最大特点是将装配应力耦合在交变温度场中,使有限元分析更符合工程实际。
(2)形位误差引起装配的变形随这倾斜角的增大而增加,到一定程度时达到最大保持不变,随着倾斜角的增加,径向刚度会随之增加,且伴随着过盈量的增加而线性增加。
(3)在交变温度场和形位误差装配的共同作用下,轴承内圈和相应的安装件都会发生热变形,且轴承内圈的变形量大于输出轴变形量,当变形量达到一定程度时内外圈的表面接触压力减小至0。此时的轴承会打滑致相对转动产生装配失效,当接触压力过大时,轴承摩擦力矩增大导致轴承锁死。故在航天轴承应用时可通过控制安装过盈量、设计轴承的初始径向游隙来控制轴承游隙的变化。分析结果可为该类轴承的应用提供参考。
