基于IBA-BP神经网络的物流中心选址研究

罗 东

（陕西服装工程学院，陕西咸阳 712046）

在新时代背景下，物流业越来越凸显其在社会经济发展过程中占有的不可或缺的战略地位［1-3］. 在整个物流网络运行过程中，物流中心作为供货点和需求点之间的沟通桥梁，在物流系统中有着极其重要的作用，因此选取合适的物流中心将对物流经济效益的提高产生重要影响. 我国物流行业存在起步较晚，物流系统存在结构不完善和企业经验少等诸多问题，特别是物流中心选址问题存在较多的弊端，为此，众多学者对其进行了相关探索和研究.

刘育玲［4］提出，根据各替代配电站的建设和运营成本以及产品损坏和腐烂成本的计算结果，构建了一种双层规划选址模型，为物流中心选址提供了一种新的方法；王刚［5］提出，煤炭物流中心选址看作一个复杂的系统性问题，存在多种目标和要求，文章研究了层次分析法、灰色模型和模糊评价法的成功之处，用多属性指标体系对目标进行综合性的评价；Yang等［6］针对生鲜农产品物流配送中心选址存在的不确定性，以预算成本参数为例，建立了基于主成分得分最大化的稳健模型，很大程度上改善了物流选址难的问题，提高了效率；陈姝宇等［7］针对呼和浩特市农产品物流配送的实际情况，根据交通条件、地理条件、地价、政策需求等八项影响因素构建农产品配送中心选址的评价指标体系.

以上方法虽然很大程度上对物流选址提供了一种方法，但这些方法存在一些问题. 首先，通过专家打分法来确定影响物流中心的权重，人为因素较为严重；其次，利用层次分析法确定物流中心选址问题，虽然可以弱化人为因素，但值得注意的是利用层次分析法的前提是要求影响物流的因素之间必须相互独立，但现实是指标之间往往存在相互依赖的关系；最后，学者利用模糊综合评判法时，影响物流中心的因素权重又无法具体给出. 由于智能算法拥有较好的寻优能力和求解精度，在物流中心选址问题研究过程中得到了较多学者的关注和青睐.

仇明艳等［8］提出一种基于DEA-GP方法来解决应急物流中心选址问题，将传统选址问题和DEA-GP 方法相结合，通过调整不同目标的优先级和目标值，帮助制定应急物流中心的选址决策；赵世安和屈迟文［9］采用基于适应度值排序的自适应方法改进基本布谷鸟算法的惯性权重，以平衡算法的全局开发能力和局部探索能力；韩庆兰和梅运先［10］利用BP神经网络模型对物流配送中心选址地点，从地质条件、运输、水文等八个因素入手进行合理决策，取得了较好的效果；夏晶和黄凯［11］将BP神经网络和模糊综合评价法相结合，建立了四级综合评估指标体系；刘娟和刘祥伟［12］提出一种改进的BP神经网络模型，基于8个指标建立了相对应的模糊评价矩阵，从定量和定性两方面进行，在10个方案中选出最优物流中心选址，验证了改进BP算法是科学有效的；倪卫红和陈太［13］采用免疫算法时单点交叉会产生超级个体以及固定概率会影响搜索能力的情况，分别以均匀交叉和自适应化的方法，在原算法上做出改进，为物流中心选址问题研究提供了一种更好的方法；张丹露［14］提出影响物流配送中心选址的因素存在很多，如何精确选址优化问题亟待解决，最后，文章中将免疫规划算法引入到物流配送选址优化中，证明了所提出的免疫优化算法来改善物流选址问题的有效性；汤杼彬［15］提出基于和声搜索算法的多层级物流中心选址问题，利用和声算法来优化物流中心选址问题，通过验证得到改进后的算法拥有更好的效果；徐小平等［16］提出求解物流配送中心选址问题的蜘蛛猴算法，改善了物流中心选址难的问题，提高了选址的效果；刘善球和樊兵鹏［17］借助遗传算法优化和改进快递物流配送中心选址，提高了算法的性能和节省了选址时间；赵江利［18］将改进蚁群算法应用到低碳物流配送中心优化选址系统中，通过仿真结果表明，基于改进蚁群算法的选址系统具有更强的收敛性能，指标碳排放更趋近于理论值；裴时域和李元香［19］提出一种改进的模拟退火算法，并和物流配送中心选址相结合，解决了物流选址困难的问题.

在以上学者研究的基础上，文章提出一种基于IBA-BP神经网络物流选址方法，从而在运行Matlab软件时，训练速度更快、误差更小，能更迅速准确地选取最优选址方案.

1 蝙蝠算法及其改进

1.1 原始蝙蝠算法

蝙蝠算法是学者Yang于2010年通过模拟蝙蝠发出声呐来寻找食物和躲避障碍物行为提出的一种新型智能算法［20］. 和其他智能算法一样，BA算法全局搜寻能力强、算法易实现、可用范围广，日益成为学者们研究的焦点.

蝙蝠算法原理：初始化每个蝙蝠个体的位置和速度，将每个蝙蝠位置作为求解最优化问题的解，求出每个蝙蝠个体所对应的适应度函数值，然后随着迭代次数的增加，通过调整脉冲速率和响度，蝙蝠朝着最优蝙蝠位置移动，最终寻找到全局最优解.

假设第i只蝙蝠在时刻t的位置为，速度是，那么在下一时刻蝙蝠的位置和速度更新公式为：

其中：Fi、Fmax和Fmin分别代表了第i个蝙蝠其在当前位置的频率、声波频率的最大值和最小值；β为0到1中的一个随机数；x*代表了当前最优解.

若rand＞R，最优蝙蝠会按照公式（4）生成新的局部解：

上述公式描述的是蝙蝠算法局部搜寻过程. 其中：R表示脉冲频率；xold代表了从当前最优解中随机选的一个；ε为-1到1的一个随机量；At代表了蝙蝠种群响度的平均值.

蝙蝠算法在觅食过程中，随着蝙蝠和猎物距离的接近，响度A(i)逐渐减小，但r(i)会随着接近猎物而提高. 蝙蝠i的响度和发射速率更新公式如下：

其中：0 ＜α＜1 和λ＞0 都是常量. 随着迭代次数的增加，蝙蝠与猎物的距离越来越近，蝙蝠发出的响度会逐渐降低到0，而脉冲发射速率会逐渐升高.

1.2 改进蝙蝠算法

拟蒙特卡罗方法的基本原理是通过确定性的超均匀分布来替换随机数序列. 由于其均匀性，将引用拟蒙特卡罗方法中的Hammersley序列对蝙蝠个体位置进行更为合理地初始化.

Hammersley序列是通过将给定的整数表示成某个素数的形式，下面为Hammersley序列的生成步骤.

1）对任一自然数n，都可以用设定好的素数p来表示：

2）用基数生成的表达式的系数{am,…,a2,a1,a0}，进行反序排列，并在前面加上小数点，求解

3）对于整数n，设置对应的维度d，可以得到d维空间的均匀序列值：

其中：p是根据维度确定的素数；p1是第一个素数；pd-1是所选的最后一个素数. 通过拟蒙特卡罗方法初始化的蝙蝠种群拥有更为合理的位置，提高了种群的多样性.

其次，针对原始蝙蝠算法飞行速度恒定不变，导致算法多样性较差、求解精度低的问题，因此提出一种新型自适应速度因子，根据算法迭代过程，自适应调整飞行速度. 在算法迭代前期，较大的速度可以增大解得搜索空间，在迭代后期，自适应减小算法的速度，以提高解的精度. 下面为自适应速度调整因子公式：

其中：t为迭代次数，tmax为最大迭代次数.

改进后蝙蝠算法步骤如下：

Step1 初始化蝙蝠算法参数，利用拟蒙特卡罗方法初始化蝙蝠种群位置，随机产生响度A和脉冲速率R；

Step2 初始蝙蝠位置，找出全局最优个体并记录最优位置；

Step3 在种群迭代过程中，蝙蝠调整频率仍为公式（1）进行调整，速度变化调整为公式（10）：

Step4 利用适应度来进行评测蝙蝠个体，更新最优值；

Step5 随机产生rand，若rand ＞R，则进行局部搜索，生成新解；

Step6 利用公式（5）和公式（6）更新A和R；

Step7 完成一次迭代，判断结果是不是达到最大迭代次数或者满足设定的求解精度，则输出最优位置以及最优值，否则转到Step3.

1.3 仿真实验

选取10个测试函数分别对BA、CS和IBA进行仿真实验，参数设置为：种群规模n=40，最大迭代次数为1000，最大脉冲音强A=0.25，搜索脉冲频率范围［-1，1］，最大脉冲频度R=0.5. 操作系统为Windows 10，测试平台为Matlab7.0，IBA、CS 和BA 均独立运行1000 次. 在固定最大迭代次数前提下，测试BA、CS 与IBA 的收敛速度、寻优精度. 测试函数定义及基本特征见表1，测试函数最优值变化趋势图见图1～图10，三种算法搜索到的最优值、最差值、平均值和算法搜寻时间见表2.

图1 Ackley函数迭代曲线图Fig.1 Iteration curves of Ackley function

图2 Bohachevsky函数迭代曲线图Fig.2 Iteration curves of Bohachevsky function

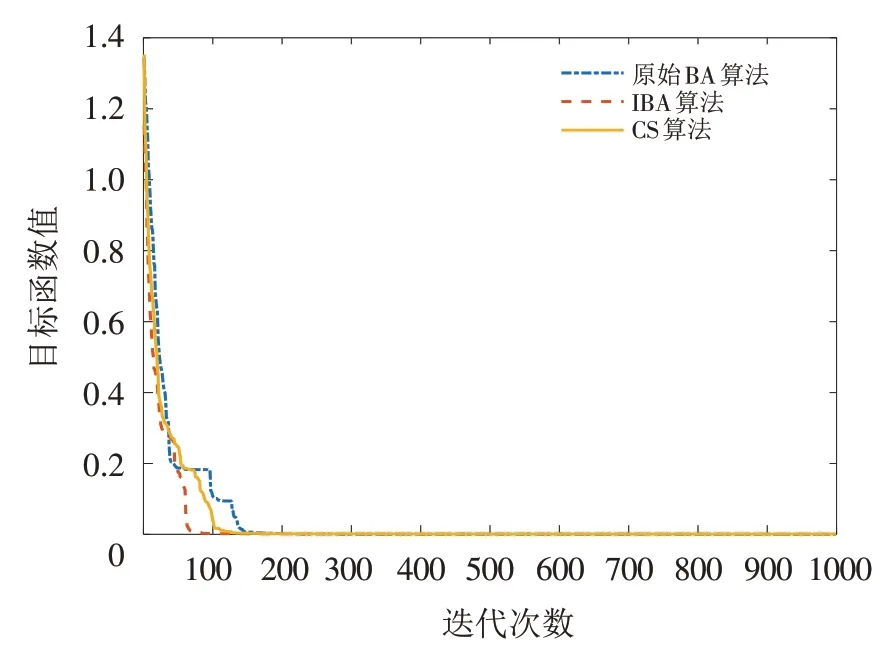
图3 Booth函数迭代曲线图Fig.3 Iteration curves of Booth function

图4 Griewank函数迭代曲线图Fig.4 Iteration curves of Griewank function

图5 Hump函数迭代曲线图Fig.5 Iteration curves of Hump function

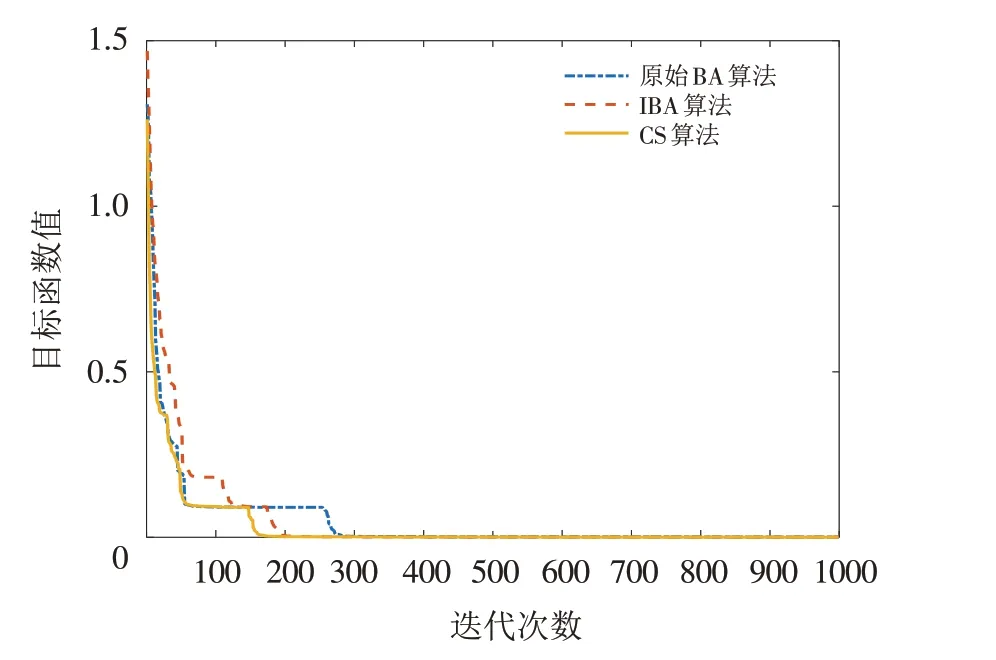
图6 Rastrigin函数迭代曲线图Fig.6 Iteration curves of Rastrigin function

图7 Rosenbrock函数迭代曲线图Fig.7 Iteration curves of Rosenbrock function

图8 Zakharov函数迭代曲线图Fig.8 Iteration curves of Zakharov function

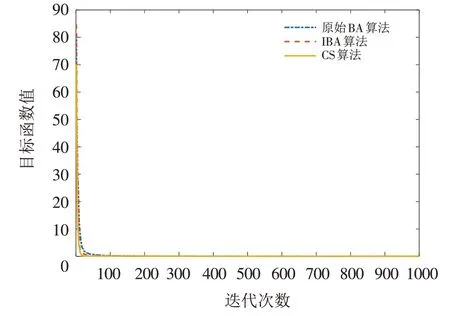
图9 Beale函数迭代曲线图Fig.9 Iteration curves of Beale function

图10 Matyas函数迭代曲线图Fig.10 Iteration curves of Matyas function

表1 测试函数Tab.1 Test functions

表2 IBA算法、CS算法和BA算法的求解精度对比Tab.2 Comparison of solution accuracies of IBA algorithm，CS algorithm and BA algorithm

为了展示改后算法的性能，已将效果最好算法进行加粗处理. 由表2 可知，一方面，对于Ackley 函数、Bohachevsky 函数、griewank 函数、Hump 函数、Beale 函数和Matyas 函数，IBA 算法搜索到的最优值、最差值和平均值均收敛于测试函数本身的最优解，这说明IBA算法在求解精度上更加优于BA算法和CS算法；对于其他函数，IBA算法在收敛精度上优于BA算法和CS算法；同时，通过收敛速度可知，就Booth函数而言，CS算法和IBA算法收敛速度相同，对于Matyas函数而言，CS算法收敛速度比IBA算法要快，对于其余8个测试函数，IBA算法收敛速度明显优于BA算法和CS算法. 另一方面，对于Hump函数而言，BA算法和IBA算法收敛时间相同，均为9 s，对于其他函数，IBA算法收敛时间均比BA算法和CS算法要短.

由图1可知，在迭代1000次的条件下，原始BA算法收敛速度较慢，在迭代200次时收敛，CS算法在迭代次数为550 次时收敛，改进后的蝙蝠算法在迭代初期收敛速度就非常快，在第20 次出现拐点，进入局部最优，然后跳出局部最优，在迭代100 次时收敛到最小值，收敛速度远远优于原始蝙蝠算法和布谷鸟算法；由图2可知，原始BA算法收敛速度较慢，在300次时才收敛到最小值，改进后的蝙蝠算法和布谷鸟算法收敛速度较快，但二者相比，IBA算法收敛速度仍快于CS算法；由图3～图7可知，IBA算法和CS算法的收敛速度均优于BA算法，但通过对比收敛到最优解的程度，IBA收敛精度远远优于BA算法和CS算法；从图8～图10中可以看出，IBA算法、CS算法和BA算法在算法迭代初期，收敛速度均非常迅速收敛到最优解，通过对比三者的收敛精度，可以看出IBA算法拥有更好的算法性能.

2 IBA-BP神经网络的物流模型

2.1 BP神经网络

BP神经网络是一种应用最为广泛的人工神经网络，其学习分为两部分：正向传播和反向传播，其主要原理是通过对输入样本数据进行训练，通过不断修正网络连接权值等参数使误差函数沿着负梯度方向下降，进而达到逼近期望输出的目的. BP神经网络采用误差反向传播学习算法，网络结构由输入层、隐含层和输出层组成. 输入层和输出层都只有一层，隐含层可以为一层或多层，同层的网络节点之间没有连接. 其中，在BP神经网络中，以单隐层的BP神经网络为最多. 单隐层的BP神经网络结构如图11所示.

图11 单隐层神经网络结构Fig.11 Structure of single hidden layer neural network

2.2 IBA-BP神经网络物流中心选址模型

下面利用改进的蝙蝠算法来搜索BP神经网络的初始权值和阈值，从而对BP神经网络进行优化. IBA-BP算法步骤如下.

步骤1：利用拟蒙特卡罗方法随机生成m个蝙蝠位置x(t)=[x…,]T，并使用每个蝙蝠位置作为一组初始连接权值和阈值，并通过BP网络权值和阈值进行排序. 蝙蝠位置的维度为：输入层的节点数目×隐层节点数目+隐层节点数目+隐层节点数目×输出层节点数目+输出层节点数目. 将权值和阈值解码，计算每组蝙蝠位置的预测误差，得到当前最优位置(i=1,2,…,n)以及最好的适应度值；步骤2：根据改进的蝙蝠飞行速度更新如下式：

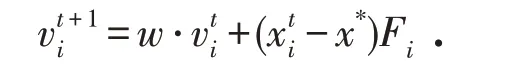
其中：w为速度因子，在蝙蝠位置更新过程中引入动态变异机制，位置变化调整为公式变异概率机制进行调整，当rand ＜p(t)时，则执行公式：

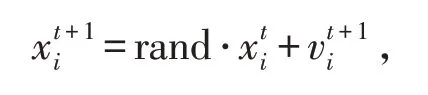
对其他蝙蝠位置进行更新，其中，将新的位置与原始蝙蝠位置进行比较，留下适应度较好的位置，得到一组较好的蝙蝠位置；

步骤3：在BA算法的局部搜寻过程中，如果rand ＞R，则更新新的解决方案；

步骤4：判断搜寻到的最优值的误差是否达到所需精度或者达到最大迭代次数，若满足，则停止搜寻，输出最优值，否则返回步骤2继续迭代；

步骤5：对蝙蝠算法搜寻到的最优解进行解码处理，并作为BP网络的最优初始参数.

2.3 建立模糊评价矩阵

物流中心的选取，一般要遵循经济性原则、适应性原则和战略性原则. 影响物流中心的因素有很多，主要分为以下几类：自然因素、交通运输条件、经营环境、政府支持、公共设施等几大类. 通过查阅相关文献和历史资料，经过细化得到以下八个影响物流中心选址的指标：地质条件、交通运输、水文条件、候选地地价、经营环境、通信条件、候选地面积、道路设施. 为了建立评价指标和评价结果间的模型，采用模糊评价法，根据以上八个影响指标对物流中心的影响程度，采用不同的隶属度函数，来得到相对应的模糊评价矩阵，如表3所示.

表3 模糊评价矩阵Tab.3 Fuzzy evaluation matrix

表3中的方案1～10是已经运营的企业数据资料，文章将此作为BP神经网络的训练数据，方案11～20作为物流中心选址的测试数据，利用MATLAB 软件分别建立BP神经网络算法、BA-BP 算法、IPSO-BP 算法以及IBA-BP算法. 网络参数确定：BP神经网络算法的网络层数为3，传递函数为logsig和purelin算法，训练目标为e=0.000 01，学习速度为0.15，训练次数为500，蝙蝠算法迭代次数为1000. 同时运用专家赋值法给予每种方案评价，其中方案1为最好的中心选址方案. 通过对方案1至方案10的训练可以看出IBA-BP神经网络运算的结果与专家赋值法的结果相同，可以通过此算法迅速选出最好的方案.

利用MATLAB7.0软件进行编程训练，利用BP网络算法、BA-BP网络算法、CS-BP神经网络算法和IBA-BP神经网络算法对方案1 至方案10 进行训练，得到如图12～图15 所示的神经网络误差曲线，通过对比可知，IBA-BP神经网络算法收敛速度最快，精度最高.

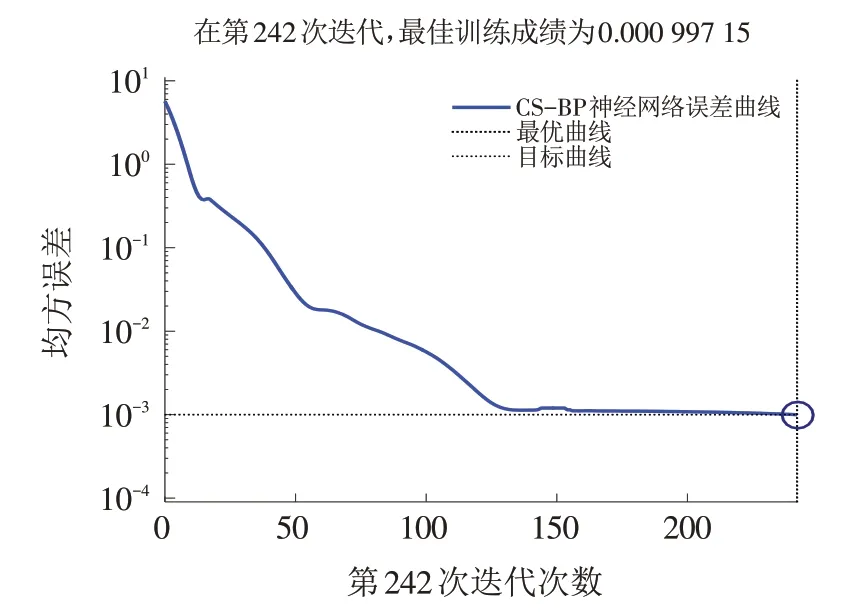
图12 CS-BP神经网络算法误差曲线Fig.12 Error curves of CS-BP neural network algorithm

图13 BA-BP神经网络算法误差曲线Fig.13 Error curves of BA-BP neural network algorithm

图14 IBA-BP神经网络算法误差曲线Fig.14 Error curves of IBA-BP neural network algorithm

图15 BP神经网络算法误差曲线Fig.15 Error curves of BP neural network algorithm

运用训练样本对网络进行训练，分别采用BP网络算法、BA-BP网络算法、CS-BP神经网络算法和IBA-BP神经网络算法对测试结果进行检验，结果如表4. 通过表4可以看出，与BP网络算法、CS-BP算法和BA-BP算法相比，基于IBA-BP神经网络算法相对误差最小，寻优精度最高，预测误差最小.

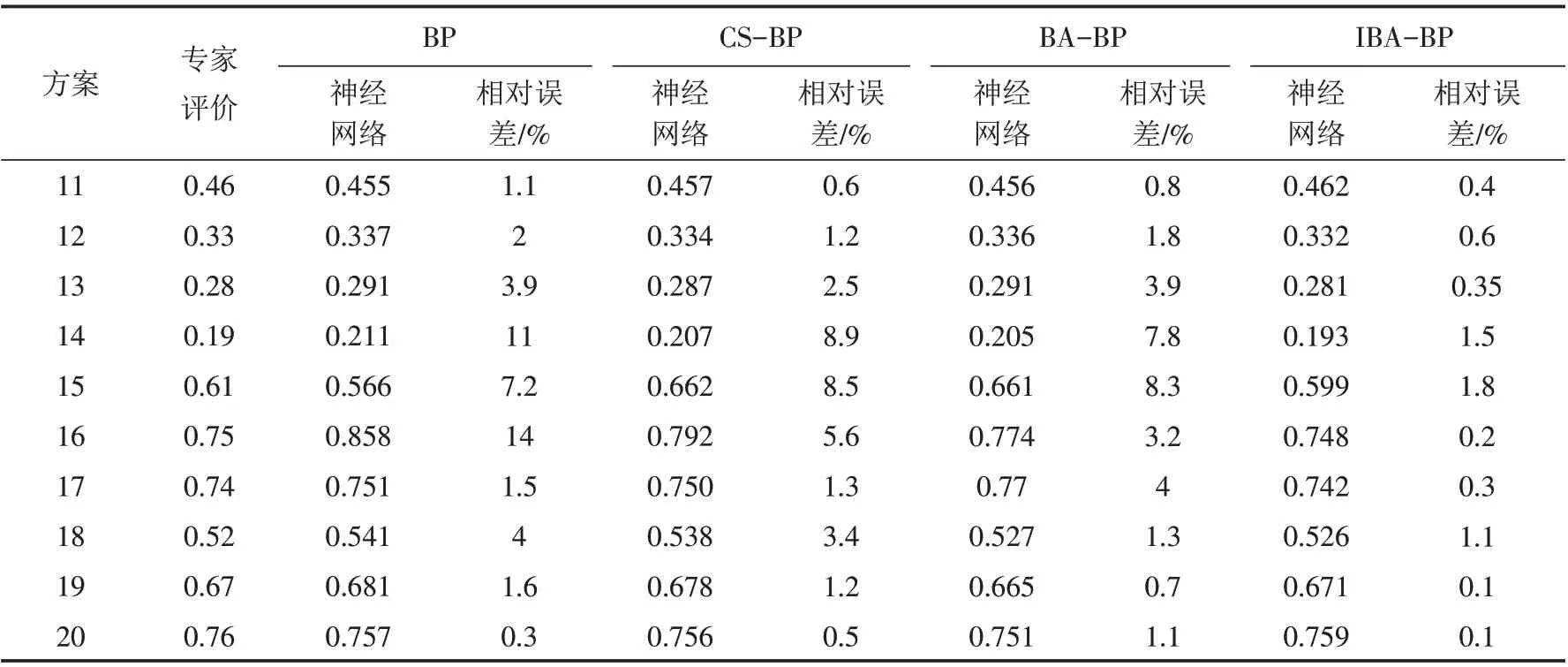
表4 BP网络、CS-BP网络、BA-BP网络与IBA-BP网络评价Tab.4 Evaluation of BP network，CS-BP network，BA-BP network and IBA-BP network

3 结论

本文以物流中心的选址作为研究对象，就物流中心影响因素构建评价指标体系，得到以下结论：为了保证指标选取的科学性，文章运用了BP神经网络算法、CS-BP神经网络算法、BA-BP神经网络算法和IBA-BP神经网络算法，通过横向对比，在MATLAB 软件中运行时可以很大程度上减少训练的误差并提高算法运行速度，解决了BP神经网络严重依赖初始权值和阈值的问题，因此，选用IBA-BP神经网络算法进行预测具有更大的优越性.