一类空气温度的随机微分方程模型
2021-11-03徐明明田德生
徐明明, 田德生
(湖北工业大学理学院, 湖北 武汉 430068)
对于温度问题的研究,主要有气象学和统计学两类方法。气象学的方法是通过对气象云图以及其他气象资料进行分析,综合太阳辐射、大气环流等因素进行分析预测。统计学的方法则通过收集历史数据,然后从这些数据中找出规律。统计学研究的常用方法和模型有最优子集回归,均生函数模型[2]等。随机微分方程自20世纪中叶发展起来到现在,其理论得到了快速发展,研究成果已经在金融、物理、生物、控制论、信息学等学科都有着广泛的应用,如金融经济学中的短期利率模型和二叉模型[1]、物理学中的布朗粒子逃逸问题等。本文拟研究全球气温的变化问题,根据气温变化的特点和大趋势,尝试建立相应的随机微分方程模型,并对其进行分析。
在1850年之前,地球的平均温度是相对稳定的。但在1860年之后,尤其是进入了工业社会以后,人类大量使用煤、石油等矿物燃料,排放出大量的CO2等温室气体。温室气体的排放是导致全球气候变暖的主要因素。从气象学的角度来说,温度的变化主要受太阳照射、地理位置、海拔高度等自然因素的影响,同时,气温也受到人类活动因素的影响,如近几十年温室气体的大量排放导致温度的持续上升,之后在各国的共同努力下低碳减排,尤其是联合国气候变化框架公约和《巴黎协定》等政策性文件的签订,使得全球气温的增长变慢。这说明全球气温的变化还是有规律可循的。
全球气温的频繁变化对生态环境和动植物的生存,乃至人类的生存都有较大的影响。在历史的长河中,全球气温就是一个时间序列,其变化既受到确定因素的影响(表现为增减趋势),又受到不确定因素的影响(表现为随机的波动性)。这种表现在理论层面上,与随机微分方程解的表现有些相似。因此,本文通过研究全球气温变化特点,建立关于气温的随机微分方程模型。
1 预备知识
1.1 维纳过程和伊藤微积分
维纳过程是一个无后效性的独立增量过程,其在大于t时刻的概率特性只与t时刻所处的状态有关,而与t时刻之前的状态无关。维纳过程也称为布朗运动(Brown)过程。我们把满足以下条件的随机过程称为维纳过程或Brown运动:
1)B(0)=0;
2)B(t),t≥0是独立增量过程且具有平稳增量;
3)对于任意的t>0,B(t)是均值为0,方差为δ2t的正态随机分量。
特别地,当δ2=1时,我们称这个过程为标准维纳过程[3]或标准布朗运动。
引理1 (重对数律[4]) 对于维纳过程B(t)有
其中,sup表示上确界,a.s.表示几乎必然。
伊藤(Ito)微积分是由日本学者伊藤清在1951年首次提出的,其目的是通过引入伊藤微积分解决随机过程微积分问题。伊藤微分公式的计算规则如下:
dt·dt=dt·dB(t)=
dB(t)·dt=0,dB(t)·dB(t)=dt
考虑随机微分方程
dX(t)=f(t,X(t))dt+g(t,X(t))dB(t)
(1)
其中:f(x,y),g(x,y)是二元连续函数,B(t)是一维维纳过程。解的形式的随机过程如下:
此时方程的解X(t)称为Ito过程,或扩散过程。
引理2 (Ito公式[5])设ξ为Ito过程,即
dξ=b(t)ξdt+σ(t)ξdB(t)
如果实值函数h(t,x)对x二次连续可微。此时,η(t)=h(t,ε)也是Ito过程。有
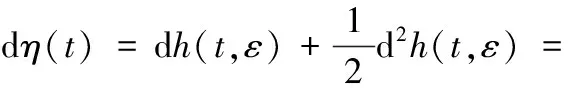
(2)
且根据伊藤微分计算规则有(dξ)2=σ2(t)dt。
假设函数H(t)是一个左连续(适应的)局部的有界过程。令Δ>0,N=t/Δ,ti=iΔ,0≤i≤Δ,此时从0到时间t,函数H(t)关于维纳过程B(t)的Ito积分是一个随机变量
由随机微分方程的相关知识可证,该极限依概率收敛。且该随机变量的期望满足
1.2 平凡解的稳定性
考虑自治的随机微分方程问题[6]
(3)
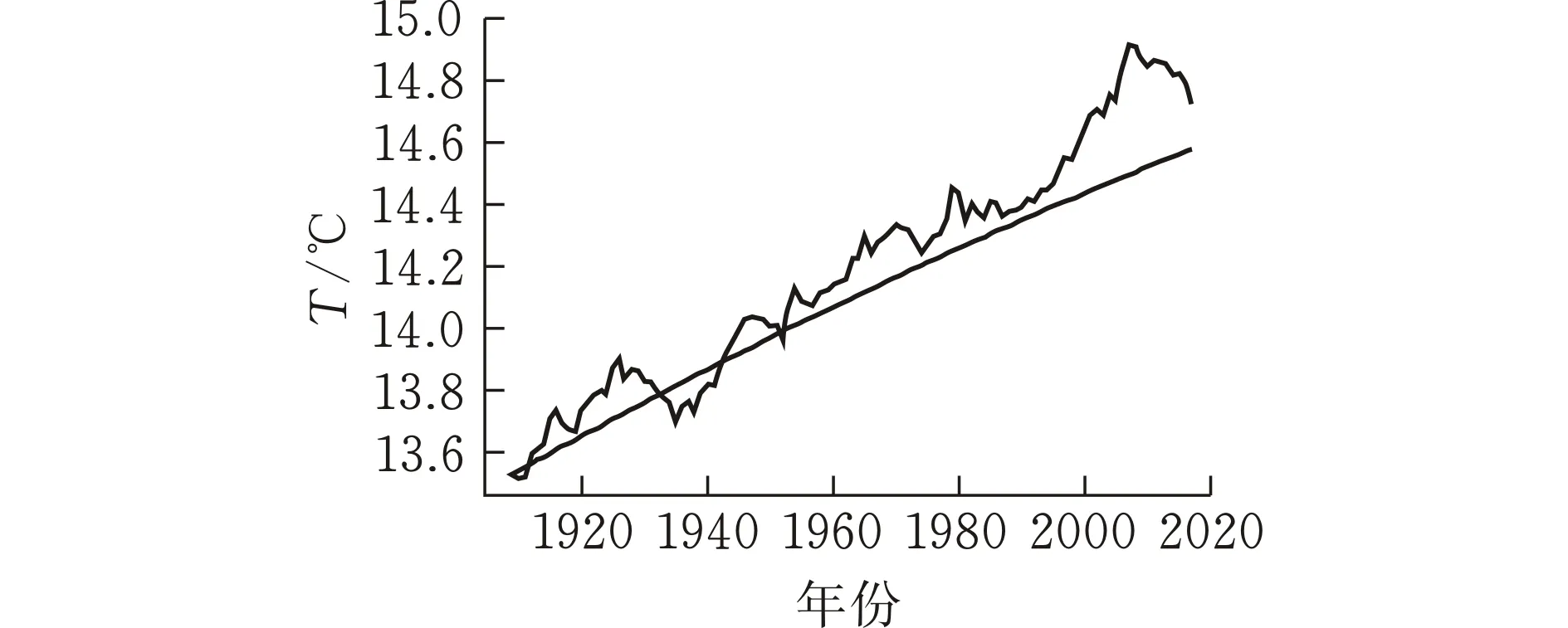
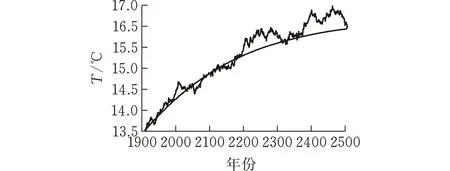
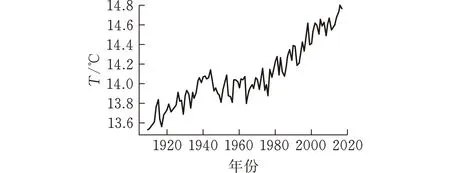
其中b(x),σ(x)是两个连续可微的函数,且满足线性增长条件。若同时满足条件|b(x)|+|σ(x)| 随机微分方程的数值计算方法有很多,其中比较经典的两种分别是Euler法和Milstein法。这里主要介绍一下最简单也是运用最广泛的Euler法。 对方程(1)的解在区间[t0,T]上进行离散化处理,然后利用Euler法构造方程(1)的连续解,其Euler显示迭代公式如下 X(tn+1)=X(tn)+f(tn,X(tn))(tn-tn-1)+g(tn,X(tn))(B(tn)-B(tn-1)) (4) 设总体ξ具有分布函数F(x,θ1,θ2,…,θk),其中θ1,θ2,…,θk为未知参数,x1,x2,…,xn是取自总体ξ的一个样本,又假设该总体的k阶原点矩μk=Eξk存在,则有矩方程组 (5) 世界各地的人类活动在不同时间段是不确定性的,导致全球气温改变的随机性。一般地,当前的气温值往往会影响下一时刻的温度变化。以T(t)表示t时刻的全球大气温度,这是一个时间序列。全球气温的变化只与当前时刻有关而与之前的时刻无关,即假设T(t)是一个维纳过程。因此,可用随机微分方程来描述全球气温模型。设f(t,T)表示人类活动量引起的温度T随时间t变化率,于是,可得如下的随机微分方程模型 (6) 其中:B(t)表示一维标准维纳过程;g(t,T)表示扩散系数。 收集1909年-2017年的全球平均温度数据,单位为作图1。 数据来源:美国宇航局戈达德研究所地球政策研究所图 1 1909年-2017年的全球平均温度 由图1可见,温度变化总体上呈现不断波动和增长势态。因此,结合式(6),以下式来描述全球平均温度模型 (7) 式中:r表示内禀增长率,α表示噪声系数。记1909年为t=0时刻,该年的平均温度为T0,即 T(0)=T0 (8) 又记方程(7)满足初始条件(8)的解为T(t;T0)。 证明 方程(7)的系数连续可微且满足线性增长条件,因此方程(7)满足初始条件(8)的解T(t;T0)存在且唯一。 对于式(7),由引理2Ito公式有 根据Ito微分计算规则,结合式(7),可得 (9) 积分式(9),并由初始条件(8)得 即 (10) 由式(10)可知,当T0>0时,恒有T(t;T0)>0,∀t>0。 证毕。 T(t;T0)的期望反映了全球平均温度的变化情况,其方差往往反映了温度的波动。下面分别讨论T(t;T0)的期望ET(t;T0)和方差VarT(t;T0)。 定理2 对于方程(7),有 ET(t;T0)=T0exp(rt),VarT(t;T0)= 证明方程(7)的解可写为如下的随机过程 对该随机过程两边取期望,并结合引理3,有 等式两边对t求导可得 因此,对方程进一步求解可得 ET(t;T0)=T0exp(rt) 对T2(t;T0)由引理2Ito公式可得 dT2(t;T0)=(2r+α2)T2(t;T0)dt+2αT2(t;T0)dB(t) 其随机过程为 等式两边取期望有 同理,等式两边对t求导,再进一步求解可得 证毕。 考虑方程(7)的参数估计。令lnT(t;T0)=x(t),记lnT0=x0。 则式(9)变为 (11) 对于Δt>0,以等距时间点列0,Δt,2Δt,…,nΔt。 离散化方程(11)可得 其中εi(i=1,2,…,n)是独立且均服从标准正态分布。因此由矩方程组(5)可设 解这个方程组,并且注意到有 因此 所以,有 其中,Ti表示第i(i=0,1,2,…,n)年的平均温度。 由定理2知,当t→∞时,有ET(t;T0)→∞(t→∞), 即随着时间的推移,温度会无限增长。显然这与实际情况不符,因为自然资源毕竟有限,有限的环境条件会对温度的增长起到阻滞作用,全球温度的上升会逐渐变慢并最终会在某个温度附近波动。基于此,建立一个关于温度的随机阻滞增长模型 (12) 其中Tm表示环境容纳量,即自然资源,环境条件所能容纳的最高温度。根据引理2Ito公式有 再将式(12)代入,可得 (13) 仍记方程(12)满足初始条件(8)的解为T(t;T0),对式(13)积分有 (14) 证明当初始值T0>0时,根据式(14),显然有T(t;T0)>0。再对式(12)进行变形,有 (15) 则根据式(15)有T(t;T0) 证毕。 受到自然资源等各种客观因素的限制,环境容纳量的值是一定的,因此,借助R语言软件中的deSolve包对Tm值进行估计,得到的结果为Tm=16.6224。对于方程(12)其Euler显示迭代公式为 T(tn)=T(tn-1)+rT(tn-1)· αT(tn-1)[B(tn)-B(tn-1)] 由此可以模拟得到含随机扰动项和不含随机扰动项的模型拟合效果(图2)。 图 2 模型拟合效果 图2中,直线表示不含随机扰动项的阻滞增长模型,曲线表示模型(11)所拟合的效果。由于内禀增长率r值较小,因此,不含随机扰动项的模型增长缓慢,在短期内图形呈直线增长。显然本文拟合的随机阻滞增长模型更加合理。 进一步,对全球平均温度进行了一定量的预测(图3)。 图 3 全球平均温度预测 由图3可以看出,在未来的很长一段时间内,全球平均温度还是会呈现缓慢、波动的上涨趋势。通过数据拟合得到的环境容纳量为16.6224℃,也就是说最终在上升了2℃左右温度将趋于稳定。温度首次达到这一数值的时间t=2395,也就是再过375年左右全球平均温度才会趋于稳定,达到环境容纳值。 全球平均气温上升2℃也是我们人类可以承受的极限。2015年11月30日在巴黎举办的联合国气候大会指出:如果到21世纪末,人类还无法将全球平均气温增幅控制在2℃以下,会导致海平面上升、森林火灾、水资源缺乏等一系列灾难性后果。这个结果也与2014年联合国政府间气候变化专门委员会(IPCC)在德国柏林发布的第五次评估报告的研究结果相同。这说明本文拟合出的环境容纳量的值是准确有效的。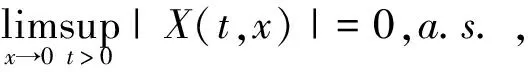
1.3 随机微分方程的数值计算
1.4 矩法估计
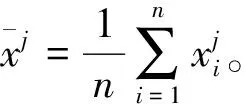
2 模型的建立与分析
2.1 气温变化的随机微分方程模型
2.2 气温变化的随机指数增长模型
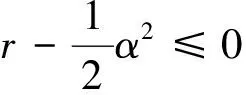
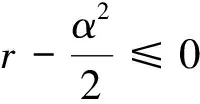
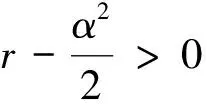


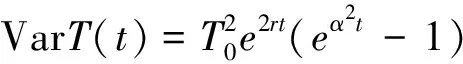
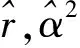
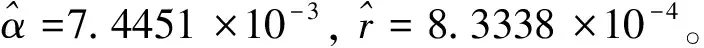
2.3 全球气温的随机阻滞增长模型
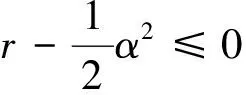
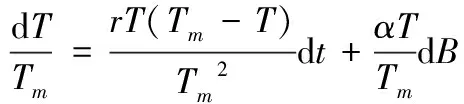
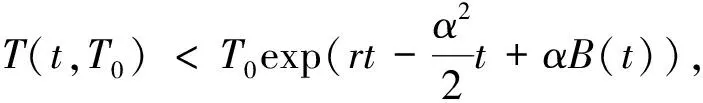
3 数值模拟