依据BP神经网络的机载LiDAR数据估算林分平均高1)

周蓉 赵天忠 吴发云

(北京林业大学，北京，100083) (国家林业和草原局调查规划设计院)

激光雷达(LiDAR)是通过激光扫描仪发射的激光脉冲测定发射器与目标物之间的距离的一种主动式遥感技术。由于激光脉冲对森林冠层的穿透性，LiDAR技术被广泛应用于森林结构参数获取。林分平均高不仅是评价森林生产力、反映林木的生长状况、判断林分立地质量的重要指标，也是反演森林生物量及蓄积量、研究森林碳储量等其他森林参数的基础[1-3]。

以机载激光雷达为技术依托，结合机载LiDAR点云数据和样地实测数据对林分参数进行估测已取得大量的研究进展，从点云数据中提取相关特征参数对林分平均高估测，是目前基于LiDAR技术获取森林树高的研究热点。ERIK et al.[4]提出基于样地尺度的点云数据，提取不同分位数上的高度和密度变量，并以此构建各种林分因子的线性回归模型；焦义涛[5]、庞勇[6]、尤号田[7]、穆喜云[8]、顾海波等[9]基于高程归一化的样方内植被点云数据，分别构建了以植被点云高度阈值平均值、上四分位数处高度值、90%分位高度值、75%分位高度值、高度变量与强度变量多变量组合为自变量的林分平均高树高线性回归模型，实验结果均表明模型对林分平均树高的估测有较好的表现，且不同的树种之间表现形式有一定的差异性。

虽然线性回归模型具有简单易懂的优点，但要求样本数据满足正态性、独立性等一定的假设限制，而实际数据往往难以满足上述假设条件，同时线性回归法也不能全面的解释各数据之间的关系，因此将非参数的估测方法引入森林结构参数反演中[10-11]。鲁林等[12]基于机载雷达点云数据提取了高度分位数变量及点云统计特征值等变量，结合实测林分平均高数据，验证了随机森林模型估测林分平均树高的可靠性；LEE et al.[13]采用3种机器学习算法—SVR、RF、RT分别建立了林分平均高模型，试验表明3种机器学习都能适用于崎岖地形和树木种类复杂的森林；ALBERTO et al.[14]以巴西的火炬松为研究对象，结合机载LiDAR点云数据与地面实测数据，采用K邻近法构建了林分平均高及优势高的回归模型，模型估测精度均在90%以上；TOMPALSKI et al.[15]为了验证模型的通用性及可转移性，基于不同点云特征变量，分别采用线性回归、随机森林、KNN 3种算法构建了不同区域的断面积加权平均高模型；赵勋等[16]采用随机森林回归和支持向量机回归两种机器学习方法，建立了广西壮族自治等区高峰林场实验区的随机森林平均高模型、支持向量机平均高模型、随机森林+支持向量机平均高模型，结果表明两种机器学习方法结合的组合模型对数据的泛化及预测能力最佳；郝红科[17]基于归一化点云数据中提取的43个变量，分别采用逐步回归法、支持向量机、快速人工神经网络方法，构建了林分平均高模型，结果表明机器学习算法的模型精度均优于线性模型；MONNET et al.[18]对比了支持向量机和最小二乘法之间的差异性，实验结果表明，支持向量机方法构建的林分优势高模型精度更佳。因此，以机载LiDAR点云数据为基础，进行森林平均高的反演具有一定的可行性，且机器学习方法能够在一定程度上弥补传统回归方法带来的不足，更好地挖掘多种点云特征变量之间的关系，为森林参数的进一步探究提供了研究思路。

但这些研究均直接采用断面积加权法得到的林分平均高作为样地实测平均高，未设置参照组对比分析；且忽略了同一种机器学习算法之间不同训练函数的差异性。综上所述，本研究以东北虎豹国家公园北部区域为研究区，分析林分加权平均高和林分算术平均高之间的差异性，在对比传统线性回归方法与机器学习算法之间优劣性的基础上，研究分析同一种机器学习算法中不同训练函数之间的差异性，以此探讨不同算法在机载LiDAR点云数据反演林分平均高模型中的适用性。

1 研究区概况

本文以东北虎豹国家公园范围内针叶纯林为研究对象，东北虎豹国家公园跨吉林、黑龙江两省，东起吉林珲春林业局青龙台林场，西至吉林省汪清县林业局南沟林场，南自吉林省珲春林业局敬信林场，北到黑龙江省东京城林业局奋斗林场，总面积共计146.12万hm2，其中森林面积130.66万hm2，森林覆盖率达89.42%，森林蓄积量1.6亿m3。研究主要范围为大兴沟、天桥岭、穆棱、东京城4个林业局及地方林场(43°20′～44°3′N，129°20′～129°55′E)，气候属大陆湿润性季风气候，地貌多为山地，年平均气温4 ℃，降水量400～800 mm，受海洋气候影响，环境湿润水系发达。植被类型属长白山植物区系老爷岭亚区，基本林分类型为温带针阔叶混交林，有野生植物约3 890种，其中主要树种为红松(Pinuskoraiensis)、云杉(Piceaasperata)、落叶松(Larixgmelini)、椴树(TiliatuanSzyszyl)、杨树(Populus)等。

2 研究数据

2.1 机载LiDAR数据获取及预处理

2018年9月，采用搭载RIEGL VQ-1560i机载三维扫描系统获取LiDAR数据，飞行实验于晴朗、无云、无风的日期开展，根据研究区的地形起伏将整个摄区分为2个区域，飞行绝对航高分别为2 300、2 100 m，最大激光脉冲频率为1 000 kHz，最大扫描频率为207 Hz。整个飞行过程的旁向重叠度控制在21%左右，点云密度约为4个/m2。

本文以LiDAR 360软件为数据处理平台，对点云数据进行去噪、地面点分类、植被点分类等预处理工作，如图1所示为预处理后样地尺度的点云数据三维效果图。从预处理的点云数据中提取与点云高程值相关的统计变量，如表1所示为提取的32个垂直结构特征变量，包括22个高度相关统计变量和10个点云密度相关统计变量。

2.2 地面调查数据获取及预处理

地面调查实验于2018年9月开展，在研究区内分别设置32块冷杉样地、43块云杉样地、53块落叶松样地，共计128个纯林样地。首先观察周围林分状况，确定圆形样地的中心点，采集中心点GPS处坐标，并记录样地的基础信息；其次在设置的半径为15 m，面积为0.07 hm2的圆形样地内进行每木检尺，获取单木的胸径、树高、枝下高、冠幅等测树因子，采用胸径尺获取每株单木1.3 m处的胸径，采用VL5激光超声波测高测距仪获得了每木树高、枝下高信息，采用皮尺测量获得了树木的东西、南北冠幅信息；最后通过差分GPS解算获得样木坐标。样地实测样木信息统计如表2所示。

图1 预处理后样地点云数据效果

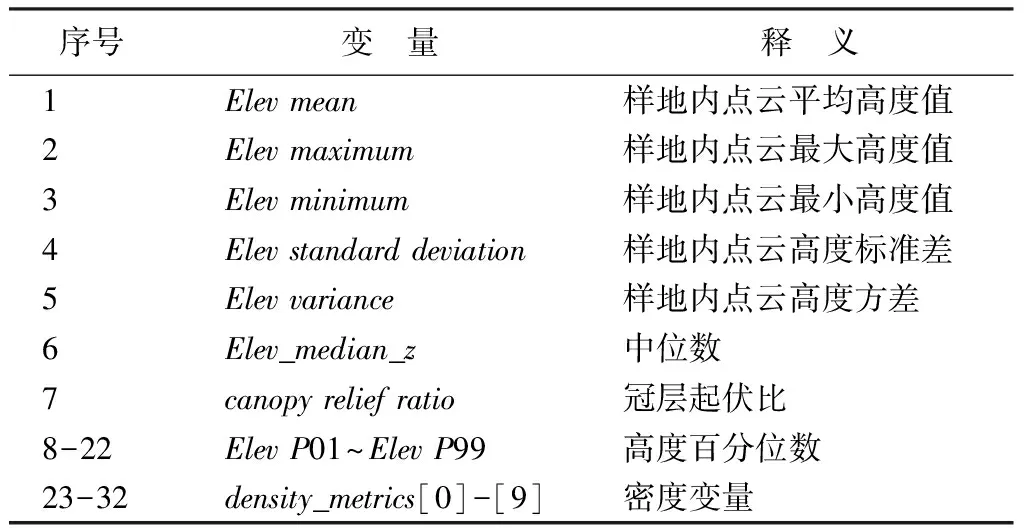
表1 32个点云特征变量统计

表2 样木调查因子统计

本文拟探究各样地的算术平均高、加权平均高之间的差异性是否会影响林分平均高反演模型的估测精度。根据公式(1)计算得各样地算术平均高，林分加权平均高采用胸高断面积加权法计算得到，计算公式如公式(2)所示。

(1)

(2)

式中：Ha为算术平均树高；Hd为加权平均高；hi为第i株立木的树高；Gi为第i株立木胸高断面积；n为样地内的立木总数。

3 研究方法

3.1 基于机载LiDAR估测林分平均高基本原理

LiDAR系统通过激光扫描仪发射激光脉冲，测量主波射出与地面采样点激光回波脉冲之间的时间间隔ΔT[19]，根据公式(3)可测算地表各点距传感器发射点之间的距离，并通过LiDAR系统自身的GPS信息确定目标物的三维坐标信息。当搭载激光雷达系统的有人机在森林上空作业时，激光雷达系统发射的脉冲信号穿透植被冠层，并接收森林树冠层、树干、地表等地面物反射的激光能量，通过计算地面和树冠顶部的激光回波的距离即能获得树高[12，20-21]。

(3)

式中：L为传感器与目标物之间的距离；C为光速；ΔT为发射主波从传感器到目标物的往返传输时间。

3.2 逐步回归模型构建

本研究基于SPSS平台开展逐步回归模型的构建，随机选择104个样本数据进行模型的构建，剩余24个样本数据作为测试样本验证模型精度。根据逐步回归算法的数学特性，分别优选了不同的变量参与林分算术平均高、林分加权平均高模型反演研究，如表3所示，给出了优选后参与模型构建的变量及具体释义。

表3 优选后参与逐步回归模型构建的因子

3.3 BP神经网络构建模型

BP神经网络是一种误差逆向传播的多层前馈神经网络，由输入层、隐含层、输出层构成，本研究中BP神经网络拓扑结构图如图2所示。分别采用贝叶斯正则化算法和L-M算法对BP神经网络进行训练，L-M算法使得模型在具有全局收敛性的同时也具有局部收敛性[22-24]；贝叶斯正则化训练算法能够有效改善拟合曲线的误差[25-28]。具体的模型构建过程如下：

(1)数据划分及归一化。本文引入验证样本数据对模型构建过程中的参数进行调整，训练样本∶验证样本∶测试样本为6∶2∶2。为了避免数据偏移分布带来的无法收敛，采用mapminmax函数对输入因子和输出因子进行归一化处理，将数据分布映射到[-1,1]区间。

(2)网络结构确定。输入层节点为32，输出层节点数为1，根据公式(4)确认隐含层范围为7～16，确认当隐含层数为7时，模型拟合效果最佳，因此确认BP神经网络模型结构为32∶7∶1。

(4)

其中：S为隐含层节点数;n为输入层的节点数;o为输出层节点数;m为1～10之间任意整数。

(3)传递函数及参数确定。设置tansing函数作为隐含层的传递函数，以线性传递函数作为输出层的传递函数；设置学习速率为0.01，最大迭代次数为1 000，目标精度为0.001，最大验证失败次数为10次。

3.4 模型评价标准

为了便于直观分析模型的精度，采用R2决定系数、P树高估测精度[5-8，12]作为本研究的模型精度评价指标，具体计算方法见公式(5)、(6)。

(5)

(6)

图2 BP神经网络拓扑结构图

4 结果与分析

4.1 逐步回归模型

当采用24个检验样本数据验证逐步回归法构建的林分平均高估测模型精度时，各模型的估测值与实测值相关关系如图3所示。

其中林分算术平均高模型，以单变量elev_median_z为自变量，图3(a)表示了该模型估测的林分算术平均高与实测算术平均高的相关关系，其决定系数R2为0.809，具体表达式为：

Ha=3.201+0.847×Elev_median_z。

林分加权平均高模型是以ElevP70、density_metrics[4]为自变量构建的，图3(b)为模型的估测值与实测值的相关关系，决定系数R2为0.858，具体表达式为：

Hd=1.884+0.819×ElevP70+1.125×density_metrics[4]。

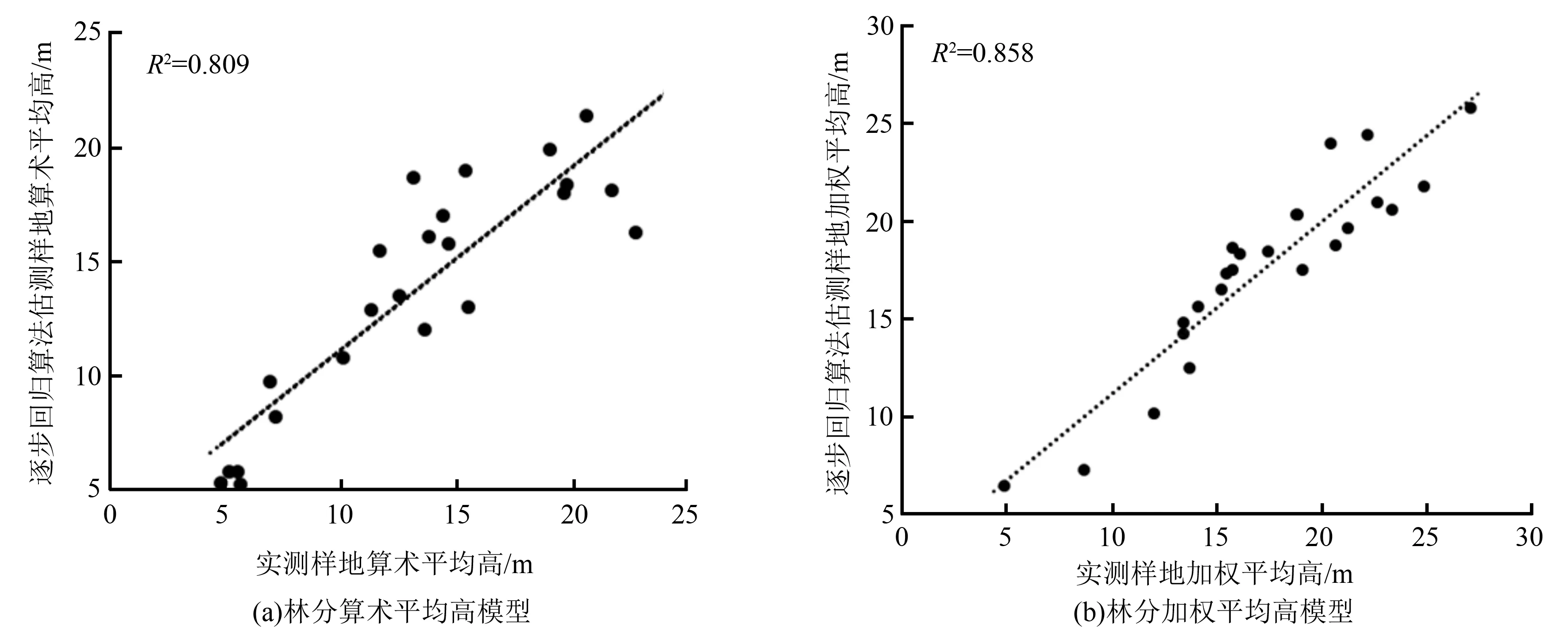
图3 基于逐步回归法估测的林分平均高与实测树高对比图

4.2 BP神经网络模型

根据获取的BP神经网络模型，分别对样地算术平均高、样地加权平均高进行预测。为检验模型的预测精度，采用24个检验样本数据进行平均高的估测，并分析了估测值与实测值的相关关系。图4为基于L-M算法构建的林分平均高模型的估测值与实测值的相关关系，其中图4(a)为林分算术平均高模型，其决定系数为0.882；图4(b)为林分加权平均高模型，其决定系数为0.919。

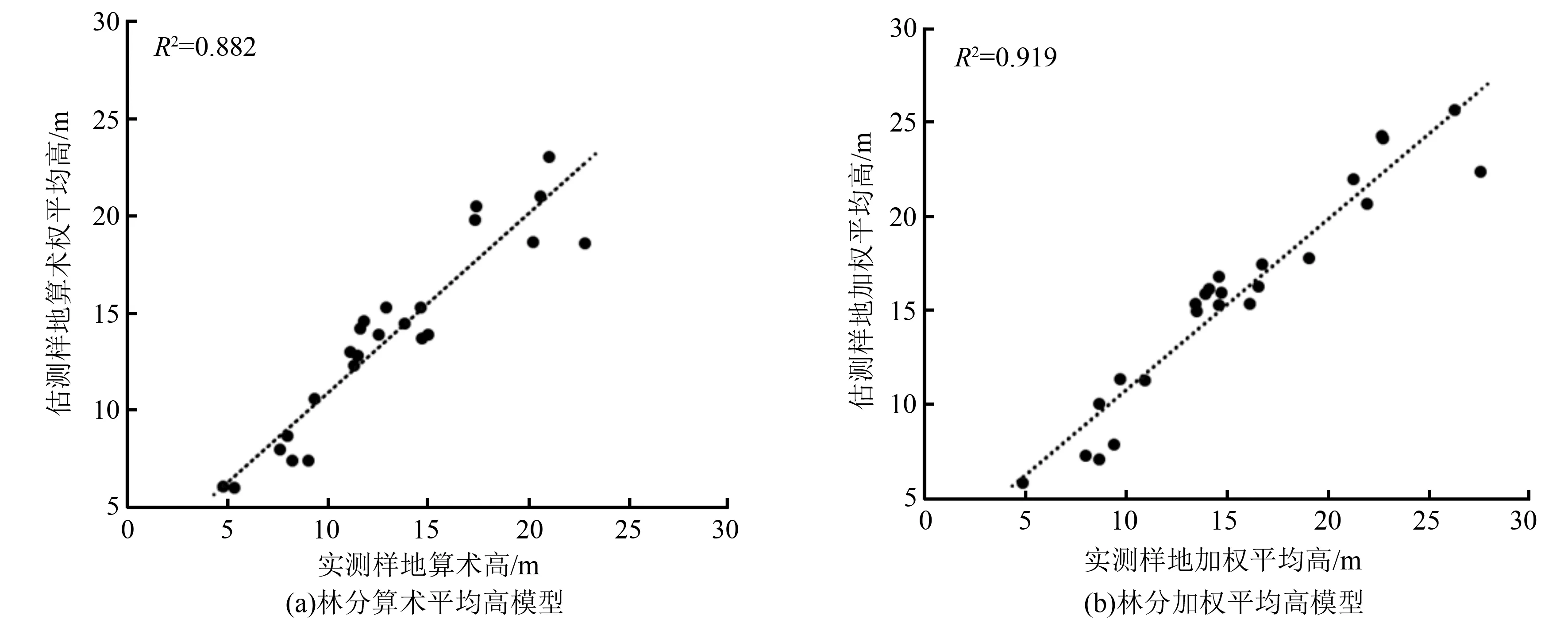
图4 基于L-M算法估测的林分平均高与实测树高对比图

如图5(a)、图5(b)所示，分别为采用贝叶斯正则化训练算法构建的林分算术平均高模型、林分加权平均高模型的预测值与实测值的相关关系，其决定系数分别为0.874、0.908。

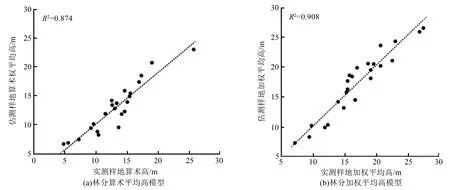
图5 基于贝叶斯正则化算法估测的林分平均高与实测树高对比图

4.3 模型结果对比分析

为了更加直观的体现实测林分平均高与各模型预测值之间的差异性，首先据公式(6)计算得各样地的树高估测精度P，且将各模型的决定系数、最高估测精度、最低估测精度、平均估测精度整理得表4；其次图6描述了逐步回归法、BP神经网络L-M算法、BP神经网络贝叶斯正则化算法分别构建的林分算术平均高模型、林分加权平均高模型估测的林分平均高预测值和样地实测值的差值。结合表4及图6对模型结果进行对比分析，具体如下。

表4 不同算法构建的林分平均高模型精度评价

(1)BP神经网络算法对数据的探究能力、模型的拟合效果优于逐步回归法。如图5所示，样地预测误差最大为逐步回归法构建的算术平均高模型中的第15号样地，其误差达到6.78 m；从表4进行分析可知，与逐步回归法对比，L-M算法平均精度提升了6.7%、贝叶斯正则化算法平均提升了5.75%。

(2)林分加权平均高模型整体拟合精度优于林分算术平均高模型。分别采用逐步回归法、BP神经网络L-M算法、BP神经网络贝叶斯正则化法反演林分平均高模型时，加权平均高作为目标值反演的模型R2比算术平均高作为目标值时分别提升了4.9%、3.7%、3.4%。

(3)对BP神经网络来说，L-M算法、贝叶斯算法在实验中表现无明显差异。L-M算法与贝叶斯正则化算法相比，其构建的模型的平均R2仅高出0.95%。

(4)检验样本数据的树高估测精度P最高为99.4%，最低为56.5%，总体平均估测精度均在85%以上，实测值与预测值无显著偏离差异，在各模型的预测值与实测值的散点图中验证了该结论。

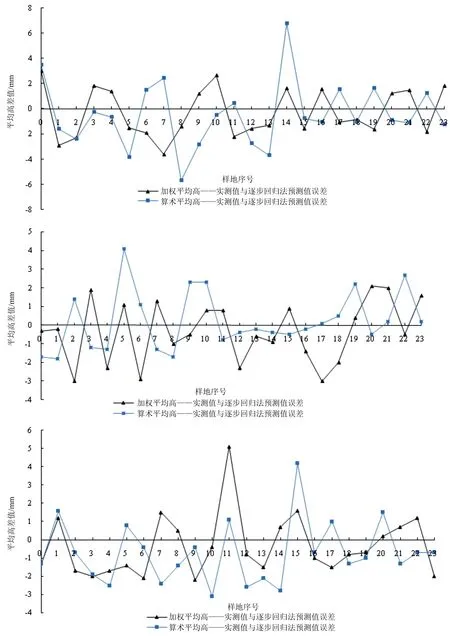
图6 各算法下估测不同林分平均高的样地实测值和预测值的差值对比图

5 结论与讨论

本文结合研究区内128块圆形样地的机载LiDAR点云数据、野外实测的样地算术平均高数据、样地断面积加权平均高数据，提取了样地区域内的32个LiDAR点云特征变量，使用逐步回归法、BP神经网络L-M算法、BP神经网络贝叶斯正则化算法对东北虎豹国家森林公园范围内的针叶纯林的林分平均高进行预测。

基于BP神经网络算法构建的林分平均高估测模型的估测精度较高，优于逐步回归法构建的林分平均树高估测模型。采用24个检验样本对BP神经网络模型进行评价，模型估测值与实际值的相关性较强，相关系数R2均在87%以上，高于逐步回归法构建的林分平均树高估测模型。可以验证该算法对林分平均高估测的可行性。BP神经网络不同的训练算法对林分平均高的估测结果具有一致性。研究比较了贝叶斯正则化训练函数与L-M训练函数的性能，在不同目标值情况下，两种不同训练方法构建的模型均能较好的预测林分平均高，虽然不同训练算法的评价精度略有差异，但整体相差较小。各样地的断面积加权平均高更适用于林分平均高估测模型的建立。对比逐步回归法及BP神经网络算法构建的估测模型发现，采用样地加权平均高作为实测值时，模型的精度提升了3.4%～4.9%。

本研究所构建的模型虽然能够较好的估测林分平均高，但由于数据量的限制，未开展区分树种的研究；且LiDAR数据与其他光学遥感数据源相结合获取相应的林分参数变量也有待进一步实验。以机载LiDAR点云数据为依托，开展其他林分结构参数的研究是笔者今后的努力方向。