一类具有恐惧和合作狩猎捕食系统的全局分析
2021-11-03刘俊利刘白茹
吕 潘,刘俊利,刘白茹
(西安工程大学 理学院, 陕西 西安 710048)
0 引 言
1948年,LESLIE在文献[1]中首次介绍了一种捕食者的生长功能反应不同于捕食者的捕食功能反应的捕食者-食饵模型,其中捕食者是逻辑增长的,受环境因素的影响,捕食者的增长依赖于捕食者与食饵的比例。从生物学的角度来看,在严重缺乏食饵的情况下,捕食者只能选择捕获其他物种作为食饵来源的一部分,但其数量的增长将受到抑制[2]。到1960年,LESLIE与GOWER改进了文献[1]中的模型,引入了功能反应项p(x)描述食饵物种受到捕食作用的影响[3]。
近年来,很多学者分析了相互作用的捕食者-食饵模型的动力学行为,并研究了Leslie-Gower模型。 NINDJIN等将时滞纳入修正后的Leslie-Gower捕食者-食饵模型,并使用构造Lyapunov函数的方法[4]研究了时滞系统的整体稳定性和持久性[5];HUANG等讨论了一个具有广义Holling III型功能反应的Leslie型捕食者-食饵系统的分岔情况[6]。
物种之间的合作是生物学中一个快速发展的研究领域,合作狩猎是物种间合作最广泛的形式[7-8]。捕食者不仅可以通过直接捕食影响食饵的物种数量,也可以间接地影响食饵的行为和生理特征[9]。与直接捕食相比,因担心被捕食而导致的行为和生理变化具有更强的持久性。研究表明,食饵对捕食者的恐惧会导致食饵的繁殖率减少,从而影响生态系统的种群动态[10-11]。很多学者分别研究了合作狩猎[12-13]和恐惧效应[14-17]对捕食系统的影响。2019年,PAL等研究了一个具有合作狩猎和恐惧效应的捕食模型,证明了解的有界性、持久性,并分析了平衡点的稳定性,Hopf分岔的存在性和分岔的方向,以及Bogdanov-Takens分岔[15]。研究结果表明,恐惧效应和合作狩猎都对捕食系统有着重要的影响。在文献[15]的基础上,本文将考虑环境因素对捕食系统的影响,并假设系数全部为ω>0的正周期函数,研究一类非自治的模型。
1 预备知识
1.1 定义与引理
考虑方程
(1)
其中p(t)、l(t)是连续的ω-周期函数,∀t∈R有l(t)≥0。定义ω-周期函数f(t)的时间平均值、最大、最小值分别为
则由文献[18]中的引理1可得如下结论:
引理1系统(1)有唯一的非负ω-周期解g*(t),且当t→∞时,g(t)-g*(t)→0,并且有
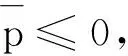
1.2重合度
设X和Y为Banach空间,L:DomL⊂X→Y为线性映射,N:X→Y是连续映射。若dim KerL=codim ImL<+∞,ImL∈Y是封闭的,则算子L是零指标的Fredholm算子;若L为零指标的Fredholm算子,连续映射P:X→X,Q:Y→Y满足ImP=KerL,ImL=KerQ=Im(I-Q),则
L|Dom L∩Ker P:(I-P)X→ImL

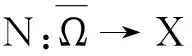
(ⅰ) ∀λ∈(0,1),x′∈∂Ω∩DomL,有Lx′≠λNx′;
(ⅱ) ∀x′∈∂Ω∩KerL,有QNx′≠0;
(ⅲ) deg{JQN,Ω∩KerL,0}≠0。
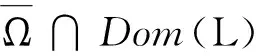
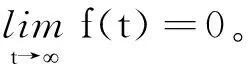
2 模型的建立
在文献[15]的基础上,假设捕食者的增长函数不同于捕食者的捕获项,而是依赖于捕食者与食饵的比率,则有如下模型:
(2)
式中:x(t)、y(t)分别为t时刻食饵与捕食者的总数;r(t)为食饵的出生率;k(t)为食饵对捕食者的恐惧程度;d(t)为食饵的自然死亡率;b(t)为食饵的种内竞争率;α(t)为每个捕食者对食饵的攻击速率;a(t)为捕食者间的合作程度;s(t)为捕食者的内禀增长率;n(t)衡量了食饵能量转化为捕食者能量的程度;m(t)为与捕食者的替代食物有关的正周期函数。以上参数均为正的连续周期函数,且有共同的周期ω>0。
3 非负性和有界性

证明∀β∈Γ,定义H(t,β)=(H1(t,β),H2(t,β))。
则H(t,β)是连续的,并且在R×Γ的每个紧子集上关于β是利普希茨的。显然,当β≥0且βi=0,i=1,2时,Hi(t,β)≥0。由文献[21]可得系统(2)过点β∈Γ的解在其最大存在区间[0,σ)上是存在的、唯一的,且为非负的。由式(2)知
由引理1可得
f1(0)>0
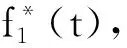

(3)
由式(3)可得,当t>T1时,有
由引理1可得
f2(0)>0


因此,∀ε2>0,∃T2>T1,使得∀t≥T2,有
综上可得,系统(2)的解是最终有界的,则σ=+∞。
4 周期解的存在性
定理2若系统(2)满足条件:
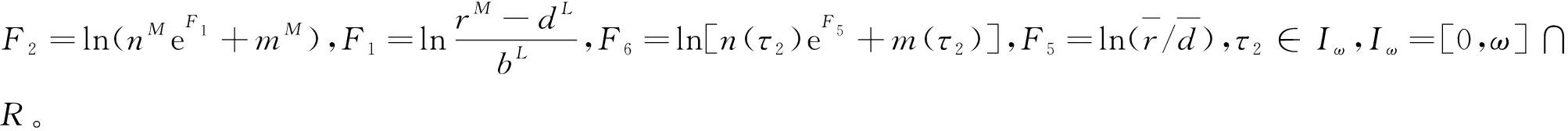
证明令x(t)=eu(t),y=ev(t),则系统(2)变为
构造集合
X=Y={z(t)=(u(t),v(t))T∈
(R,R2):z(t+ω)≡z(t)}
定义范数
‖z‖=‖(u(t),v(t))T‖=

显然,集合X和Y是赋予范数‖·‖的Banach空间。算子L,P,Q定义如下:
其中DomL={z∈X:z(t)∈C1(R,R2)}。定义N:X→Y为
容易得到
是集合Y上的闭子集;dim KerL=codim ImL=2<+∞,且P,Q都是连续映射;ImP=KerL,KerQ=ImL=Im(I-Q)。则L是一个零指标的Fredholm算子。L的广义逆算子Kp:ImL→KerP∩DomL为
所以
式中:
d(ρ)-b(ρ)exp(u(ρ))-
(α(ρ)+a(ρ)exp(v(ρ)))exp(v(ρ))
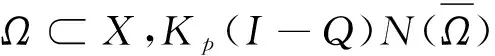
为了运用引理2分析系统(2)的周期解,需要找到合适的有界开集Ω。考虑算子方程Lz=λNz,λ∈(0,1),
(4)
由于(u(t),v(t))T∈X,则∃ξi,ηi∈[0,ω],i=1,2,使得
显然u′(ξ1)=u′(η1)=v′(ξ2)=v′(η2)=0。由式(4)可得
(5)
(6)
由假设A0易知,rM-dL>0。由式(5)可得
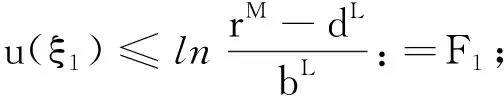
exp(v(ξ2))≤nMexp(F1)+mM
则v(ξ2)≤ln(nMexp(F1)+mM):=F2。
由式(6)的第一个式子得
则
由式(6)的第二个式子得
exp(v(η2))≥nLexp(F3)+mL
则v(η2)≥ln(nLexp(F3)+mL):=F4。
综上可得,∀t∈[0,ω],有
F3≤u(η1)≤u(t)≤u(ξ1)≤F1
F4≤v(η2)≤v(t)≤v(ξ2)≤F2
令D1=max{|F1|,|F3|},D2=max{|F2|,|F4|},D=D1+D2+D0,其中D0充分大。代数方程
的解为(u*,v*)∈R2,且满足
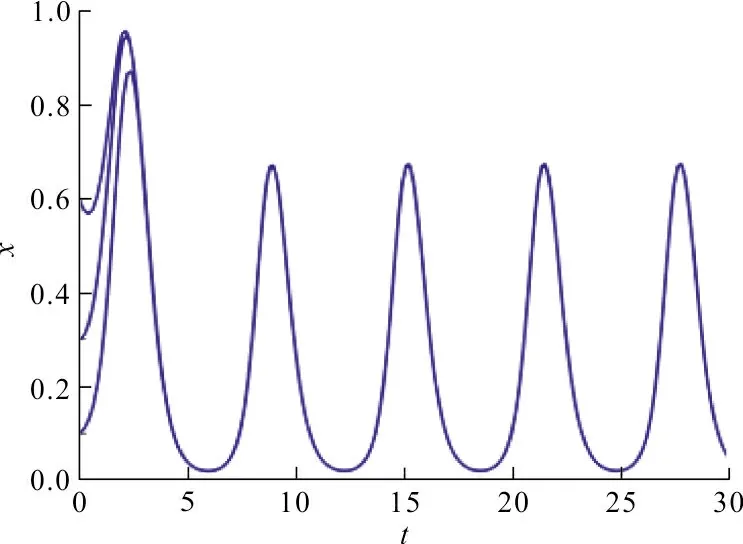
‖(u*,v*)T‖=|u*|+|v*| 显然D与λ无关。令 Ω={z=(u(t),v(t))T|z∈X,‖z‖ 当z=(u,v)T∈∂Ω∩KerL=∂Ω∩R2时,z=(u,v)T是R2中的一个常数向量,且 ‖z‖=‖(u,v)T‖=|u|+|v|=D 因此 故引理2的条件(ⅱ)成立。 由QN(z)的表达式可得,存在点τi∈Iω,i=1,2,Iω=[0,ω]∩R,使得 定义同构映射 J:ImQ→KerL,Jz≡z 且 P:DomX×[0,1] 其中μ是参数,则∀(u,v,μ)∈(∂Ω∩KerL)×[0,1],P(u,v,μ)≠0。否则,存在z=(u,v)T∈∂Ω∩KerL,μ∈[0,1]且|u|+|v|=D,使得P(u,v,μ)=0,即 (7) v≥ln(n(τ2)eF7+m(τ2)):=F8 因此, |u|+|v|≤max(|F5|,|F7|)+ max(|F6|,|F8|) (8) 当(u,v)T∈∂Ω∩DomL时,有‖z‖=|u|+|v|=D。但由式(8)可得,Lz=λNz,λ∈(0,1)的解为 则当z∈∂Ω∩DomL,λ∈(0,1)时,Lz≠λNz,即引理2的(ⅰ)成立。通过计算可得 满足引理2的条件(ⅲ)。综上可得,系统(2)至少有一个正的ω-周期解。 定理3在定理2的条件下,若系统(2)满足条件: λM+2aMeF2 F4=ln(nLeF3+mL),则系统(2)的正周期解(x*(t),y*(t))T是全局吸引的。 证明由定理2可得,系统(2)的周期解(x*(t),y*(t))T满足 eF3≤x*(t),x(t)≤eF1 eF4≤y*(t),y(t)≤eF2 假设(x(t),y(t))T是系统(2)的任意正解,定义Lyapunov函数为 V(t)=|lnx(t)-lnx*(t)|+ |lny(t)-lny*(t)| (9) 式(9)沿着系统(2)的Dini导数(D+)为 由条件B1、B2可得,存在正常数p、q,使得 D+V(t)≤-p|x(t)-x*(t)|- q|y(t)-y*(t)| (10) 则V(t)在[0,+∞)上不增。对不等式(10)积分可得 y*(t)|dt≤V(0)<+∞,∀t>0 由引理3可得 故可得系统(2)的正周期解(x*(t),y*(t))T是全局吸引的。 对于具有恐惧效应和合作狩猎功能反应的Leslie-Gower捕食者-食饵模型,在定理2和定理3的条件下,该模型存在正周期解并且在可行域内是全局吸引的。通过给参数赋值进行数值模拟,验证本文的结果。给出如下参数值: 得到系统(2)中捕食者y与食饵x关于时间t解的图形,如图1、2所示。 图 1 食饵x关于t的周期解Fig.1 Periodic solution of prey x with respect to time t 图 2 捕食者y关于t的周期解Fig.2 Periodic solution of predator y with respect to time t 图1显示系统(2)中食饵在不同的初始值之下收敛到同一个周期解,图2表明系统(2)中的捕食者也在不同的初始值之下收敛到同一个周期解,故系统(2)存在全局吸引的2π周期解,即系统(2)出现周期震荡。 本文在文献[15]的基础上,研究了一个具有恐惧和合作狩猎功能反应的Leslie-Gower捕食者-食饵模型。理论分析表明,系统(2)在一定条件下至少存在一个正周期解,并且该正周期解是全局吸引的;数值分析同样表明,系统(2)存在全局吸引的2π周期解,验证了理论结果。可见,食饵对捕食者的恐惧、捕食者之间的合作狩猎,以及环境因素都会影响捕食者与食饵的物种数量。若将这些影响因素控制在一定值内,则捕食者与食饵的数量会保持稳定。 因此,加入恐惧效应及合作狩猎对于保护野生动物,维持生态平衡有很重要的意义。
5 全局吸引性


6 数值模拟

7 结 语
