非对称氮化多孔石墨烯纳米带的电输运性质
2021-11-03夏蔡娟唐小洁
夏蔡娟,唐小洁
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
多孔氮化石墨烯纳米带(C2N-h2D)具有1.96 eV的直接能隙,是一种极具研究价值的纳米材料。作为一种典型的二维原子结构,石墨烯由于其独特的理化性质吸引了人们的关注[1-3],如高电荷迁移率、较好的灵活性和良好的导热性等[4-5]。然而,石墨烯的零带隙(Eg=0 eV)结构限制了其在纳米电子学与光电子学中的应用,尤其是在场效应晶体管(FETs)中的应用[6-9]。2015年,MAHMOOD等采用一种简单的湿化学反应,通过六氨基苯(HAB)三盐酸盐与六酮环己烷(HKH)八水合物,合成了一种新型二维材料,即多孔氮化石墨烯(C2N-h2D)[10]。该材料有着与石墨烯类似的蜂窝状结构,具有均匀分布的氮孔、晶体质量极高。通过计算和实验分别证明了该晶体拥有直接能隙,分别约为1.70 eV和1.96 eV。用该材料制作的场效应晶体管(FETs)器件的开关比高达107[11-14]。切割单层 C2N-h2D,可以分为锯齿形纳米带zC2N-h2D 和扶手椅型纳米带aC2N-h2D。大量实验表明,aC2N-h2D是具有半导体性质,而zC2N-h2D 具有金属性特质[14-16]。可见,当C2N-h2D用于分子电子学领域时,具有显著的性能和广阔的应用前景。
在对石墨烯结构的研究中,人们发现了许多吸引人的特性,包括整流特性[17-18]、NDR效应[19-21]、开关行为[22-23]、自旋滤波[24-25]等。此外,对称性在锯齿形石墨烯纳米带 (zGNRs)的电子输运中起着重要的作用[26]。例如:对称的zGNRs(带有偶数个碳原子的锯齿形链,显示一个σ镜面,沿纳米带的周期方向将纳米带平分)由于费米能级(EF)周围存在带隙而呈现非常小的电流;而非对称的zGNRs(具有奇数个碳原子的锯齿形链,没有σ镜面)表现得像具有线性电流-电压(I-U)关系的传统导体。一般通过打破σ镜像对称,可以得到具有特殊电子输运现象的zGNRs结构[27-29]。YA等设计了具有不同台阶宽度的非对称阶梯状锯齿形石墨烯纳米带(zGNRs),表现出了NDR效应和整流效应,但是其峰谷仅1.38,整流比也仅为2.78。本文选用性质更稳定的锯齿形氮化多孔石墨烯纳米带(zC2N-h2D),设计了3种非对称式阶梯状结构,系统地研究了3种非对称式结构的电输运性质。结果表明:非对称式结构的C2N-h2D纳米带的峰谷比高达272.3,最大整流比高达到17.8×103,其输运性能明显优于zGNRs。表明非对称式结构的C2N-h2D纳米带可用于开发纳米级整流器和NDR器件。
1 器件几何结构及计算方法
图1(a)所示为不同宽度(W=1.0、1.5、2.0)的锯齿形氮化多孔石墨烯纳米带(zC2N-h2D)结构图。在本文的工作中,基于zC2N-h2D结构,建立了3种非对称式的阶梯状的纳米带器件结构,如图1(b)所示。图1(b)中,WL、WR分别表示左右电极宽度,左右阶梯带宽比例分别WL∶WR=1.5∶1.0,WL∶WR=2.0∶1.0和WL∶WR=2.0∶1.5。为便于区分,将其分别命名为M1,M2和M3。构建的分子器件分为半无限长的左、右电极区域和有限长的中心散射区。
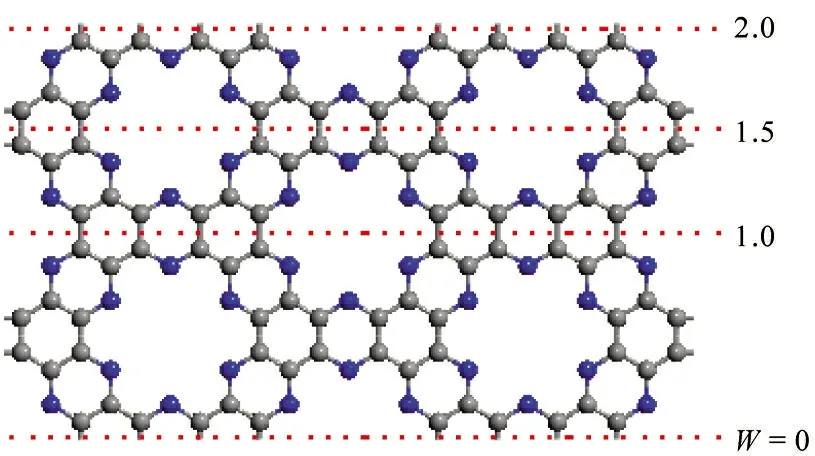
(a) zC2N-h2D纳米带的结构
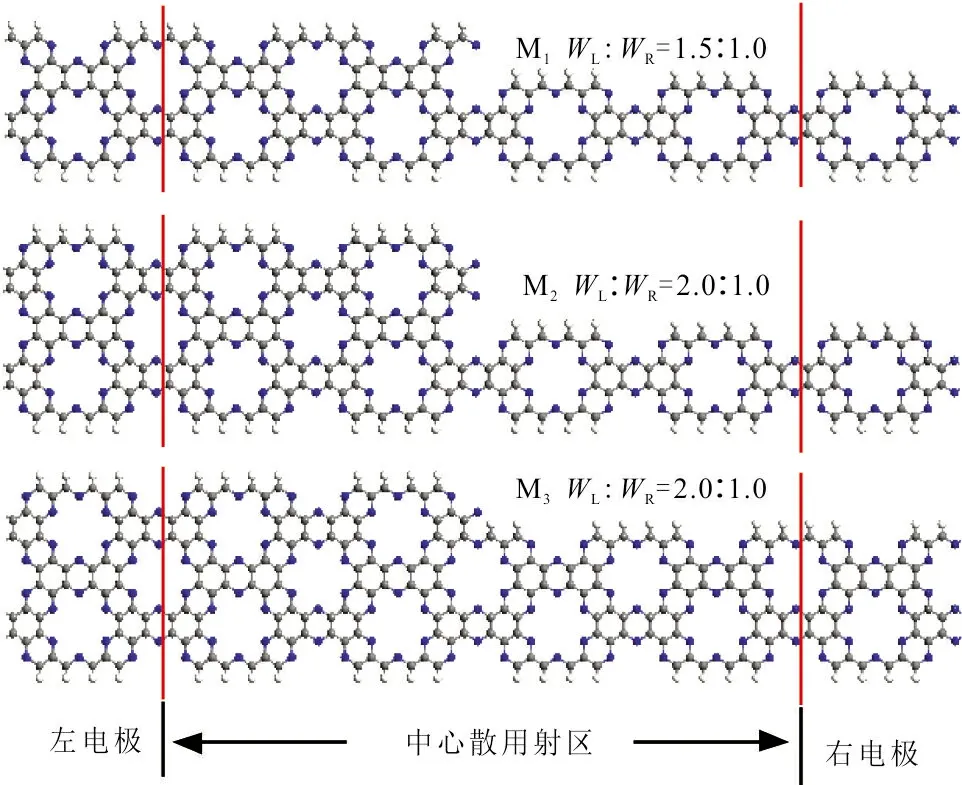
(b) 器件几何结构示意图图 1 zC2N-h2D纳米带的结构及器件几何结构Fig.1 The stracture and device geometry of the zC2N-h2D nanoribbon
通过在Atomistix Toolkit(ATK)实现NEGF+ DFT的第一性原理方法,完成所有分子器件的结构优化和电子输运计算[30-31]。结构优化时,施加到每个原子上的力不超过 0.05 eV/Å,使计算可达到良好的收敛精度。选取ζ-SZP作为相应的价电子轨道基函数,缩短模型计算过程中的收敛时间;选择150_Ry的网格截止能量,以实现计算效率和精度之间的平衡,减小误差幅度。第一布里渊区(BZ)的K点设为(1,1,100)。在进行结构弛豫和电子结构的计算中,电子交换关联泛函采用广义梯度近似(GGA)修正的 PBE 泛函,能更好的考虑到真实体系电子密度的不均匀性。器件的电流-电流特性曲线由Landauer-Büttiker公式[30]计算得出,即
T(E,Ub)dE
(1)
式中:Ub是施加的偏置电压;f和h分别表示费米-狄拉克函数和普朗克常数;μL=Ef±|e|(Ub/2)是电化学势。透射系数T(E,Ub)为
T(E,Ub)=TR[ΓL(E,Ub)·GR(E,Ub)·
ΓR(E,Ub)·GA(E,Ub)]
(2)
式中:GR/A表示格林函数,ΓL/R是电极耦合函数。
2 计算结果与讨论
图2给出了3种阶梯状zC2N-h2D结构的I-U曲线。由图3可以看出:3种结构的I-U曲线趋势具有一定的一致性,正负偏压下的曲线不对称且都存在明显的NDR效应。其中M1的电流值最大。对于M1,随着偏压增加,电流随之增大,直到0.27 V时达到最大电流6.33 μA; 之后随着电压继续增大,电流逐渐减小到接近于0 μA。对于M2、M3,随着电压增加,电流随之增大。在0.19 V和0.1 V时,分别达到最大电流值2.27 μA和1.82 μA; 之后随着电压增加,电流逐渐减小到接近于0 μA。可见,阶梯状zC2N-h2D会改变锯齿形C2N-h2D结构的性质,不同的阶梯宽度呈现出不同的电输运特性。
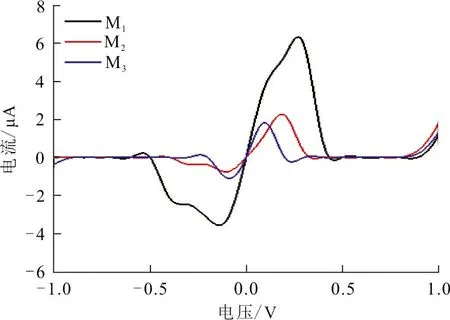
图 2 M1、M2和M3的电流-电压特性曲线Fig.2 The I-U curves of M1,M2 and M3
为了分析模型出现这种I-U特性的原因,计算并作出了3个模型在Ub=0 V时的透射谱-能量曲线,如图3所示。从图3可知,不施加偏压的情况下,3个模型在费米能级(即EF=0)附近都出现了透射谱。说明在施加偏压后,势垒很低,对电子的阻碍非常小,即说明3个模型的结构是合理的。除此之外,在费米能级附近,M1的透射透射谱与能量轴的积分面积明显大于M2和M3的。相比M2和M3,M1导致了更小HOMO-LUMO gap(HLG),进一步说明了M1的电流会比M2和M3大。
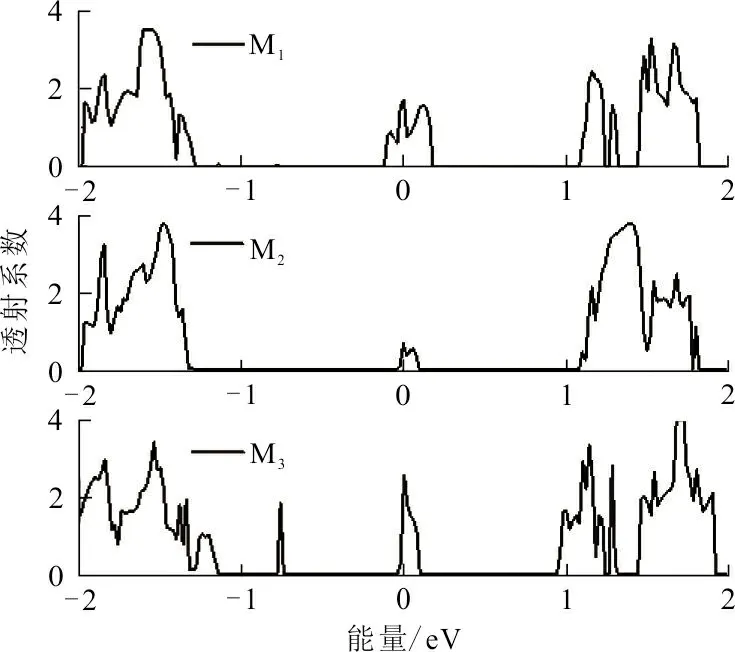
图 3 M1、M2和M3的透射谱-能量曲线(Ub=0 eV)Fig.3 The transmission coefficients-energy curves of M1,M2 and M3
为了解释模型中出现的NDR效应,分别做了3个模型在出现NDR效应电压区域的透射谱3D图,见图4。图4中红色虚线代表偏压窗为[-Ub/2,Ub/2]。
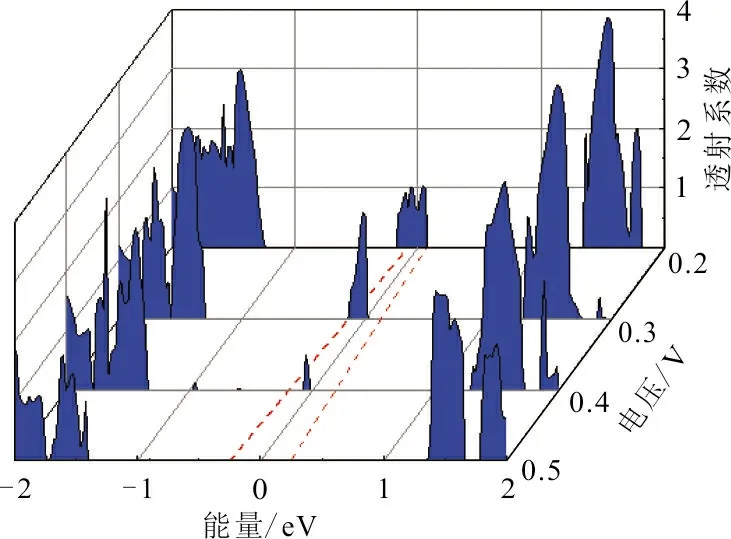
(a) Ub为0.2、0.3、0.4和0.5 V时,M1的透射谱
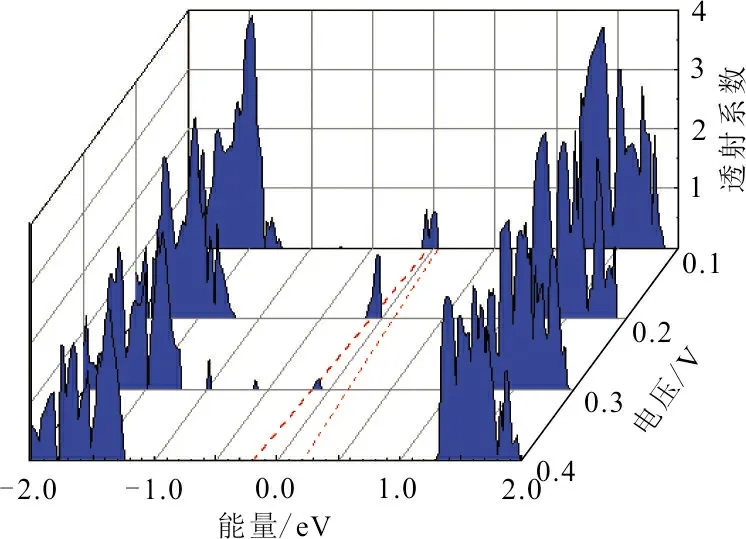
(b) Ub为0.1、0.2、0.3和0.4 V时,M2的透射谱
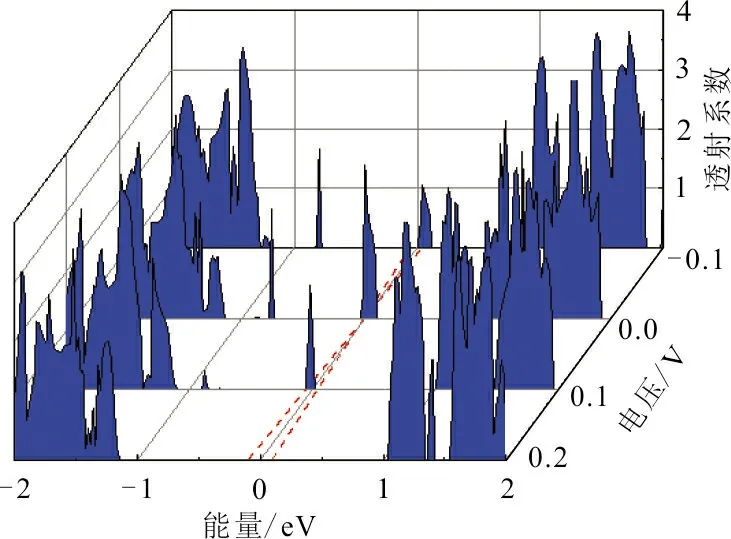
(c) Ub为-0.1、0、0.1和0.2 V时,M3的透射谱图 4 M1、M2和M3在各个偏压下的透射谱Fig.4 The transmission spectra of M1,M2 and M3 at different biases
如图4(a),计算了M1在Ub=0.2、0.3、0.4、0.5 V时的透射谱。从图4(a)可以看出,Ub=0.2 V时偏压窗内的透射系数小于Ub=0.3 V时的透射系数,而在偏压为Ub=0.4 V和Ub=0.5 V时,偏压窗内的透射系数逐渐减小。即随着电压的增加,透射系数呈现一种先增加后减小的趋势。这就解释了M1在图2中表现出的电流先增后减的现象,亦解释了M1曲线上出现的NDR现象。如图4(b),计算了M2在Ub=0.1、0.2、0.3、0.4 V时的透射谱。显然,进入BW [-Ub/2,Ub/2]的电子透射谱随着施加的偏置电压从Ub=0.1 V到0.4 V过程中,呈现先增加后减小的现象,与图2中M2的I-U曲线趋势完全吻合,解释了M2出现NDR效应产生的原因。如图4(c),计算了M3在Ub=-0.1,0,0.1,0.2 V时的透射谱,透射系数的变化趋势与M1和M2类似,在Ub从-0.1 V增至0.2 V过程中,呈现出先增后减的现象,这就解释了M3在该区域出现的NDR现象的原因。
在图2中,M1、M2和M3在正负偏压下的I-U曲线并不是对称的,表明正负偏压下电荷是不对称分布的,即3组模型均存在整流效应。据此,计算并做出了3组模型的整流比-电压曲线,如图5所示。通过计算,M1在Ub=0.2 V时达到最大整流比Rmax=17.824×103,M2在Ub=0.2 V时达到最大整流比Rmax=16.662×103,M3在Ub=0.3 V时达到最大整流比Rmax=1.852×103。
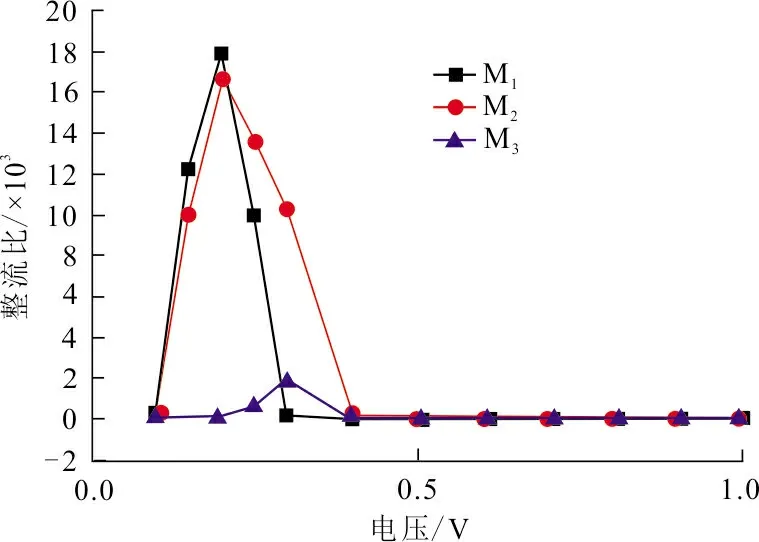
图 5 M1、M2和M3的整流比-电压曲线Fig.5 The rectification ratio-bias voltage curves of M1,M2 and M3
为了解释M1、M2和M3出现的整流比变化的原因,计算了3组模型在特定偏压下的透射谱和MPSH,结果如图6所示。图6中红色虚线代表偏压窗为[-Ub/2,Ub/2]。从图6(a)和图6(b)可以看出,M1和M2在Ub=0.2 V偏压下的偏压窗内透射系数大于Ub=- 0.2V偏压下的偏压窗内透射系数。这就解释了M1和M2正负偏压曲线不对称的现象,同时也可以说明M1和M2在Ub=0.2 V时出现最大整流比。为了更进一步验证结果的准确性,还做出了M1、M2和M3在Ub为±0.2 V或±0.3 V时的MPSH-HOMO和MPSH-LUMO,结果如图6(d)。从图6(d)可以看出:在Ub=0.2 V时,M1的HOMO及LUMO电子云分布非常密集,是离域的,对电流值有很大的贡献。因此,电子可以很轻易的越过势垒,穿越中心散射区,导致了M1在该偏压下具有较大的电流值。在Ub=-0.2 V时,M1的HOMO及LUMO电子云主要分布分子结的左侧,是局域的,而中心区域和右电极上没有轨道分布。因此,当模型的承受的电压为Ub=-0.2 V时,传输通道并不能顺利的打开,或者说打开得很小,极大地阻碍了电子的运动,导致了M1在Ub=-0.2 V时的电流值较小。同时,也解释了M1在0.2 V处出现较大整流比现象。如图6(e)所示,给M2施加Ub=0.2 V的正偏压时,HUMO的轨道空间分布在中心散射区域和右电极,而LUMO的空间轨道分散在整个分子结,所以LUMO轨道对M2在Ub=0.2 V时的电流值有很大的贡献。当施加Ub=-0.2 V偏压时,HOMO和LUMO轨道都局限于左电极,导致了较小的电流。如图6(f)所示,对M3施加Ub=±0.3 V的偏压,其HOMO和LUMO轨道都是离域分布的,导致了M3在Ub=±0.3 V下的电流值都比较小。值得注意的是,M3在Ub=0.3 V偏压时的HOMO轨道分布在左电极个中心散射区,LUMO轨道分布在中心散射区和右电极;而在Ub=-0.3 V时,HOMO和LUMO轨道仅仅分布在分子结的左电极。也就是说,M3在Ub=0.3 V时的MPSH-HOMO和MPSH-LUMO轨道的离域程度是高于M3在Ub=-0.3 V偏压时的。这也说明了模型M3中电荷是不对称分布的,以及在Ub=0.3 V时出现最大整流比的原因。
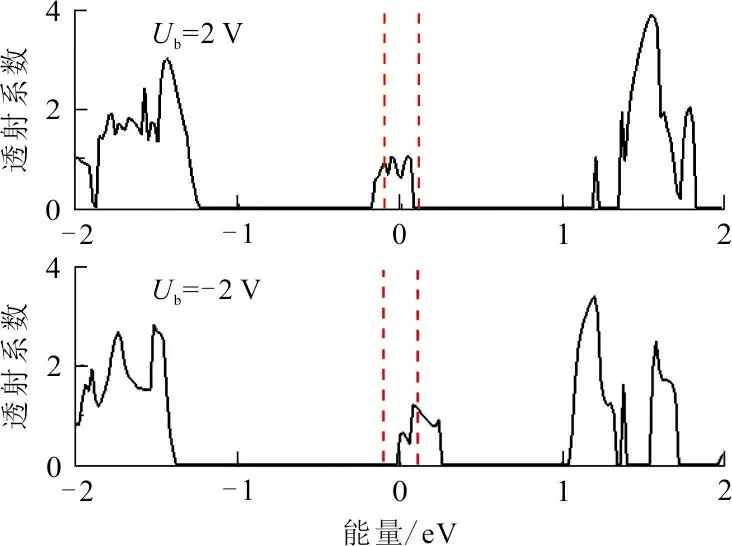
(a) Ub =±0.2 V时,M1的透射谱
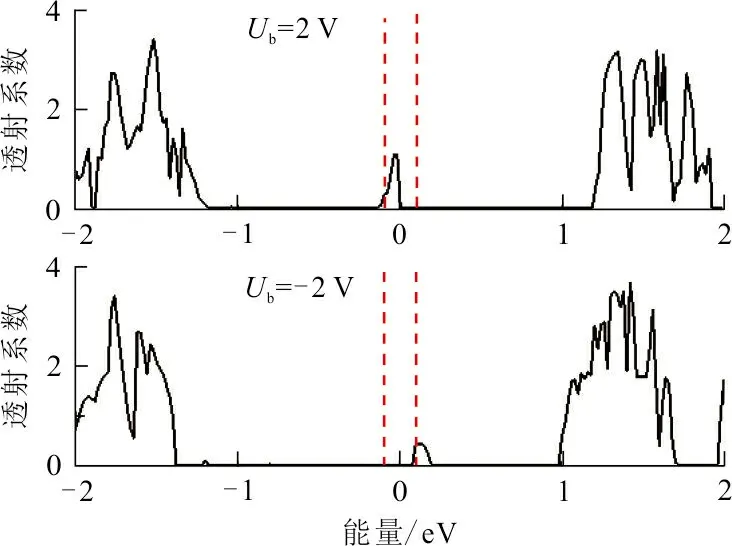
(b) Ub =±0.2 V时,M2的透射谱
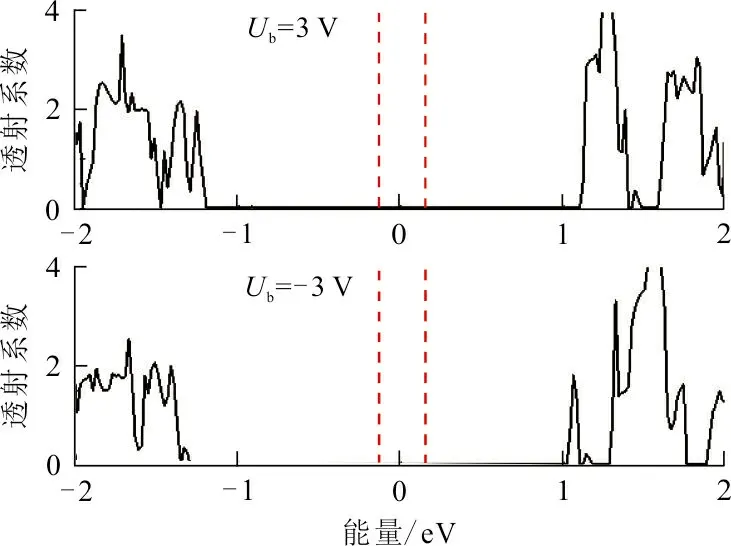
(c) Ub =±0.3 V时,M3的透射谱
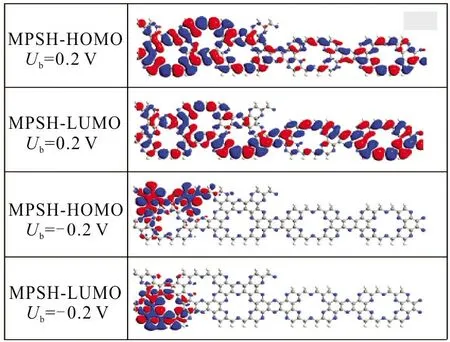
(d) Ub =±0.2 V时,M1的MPSH
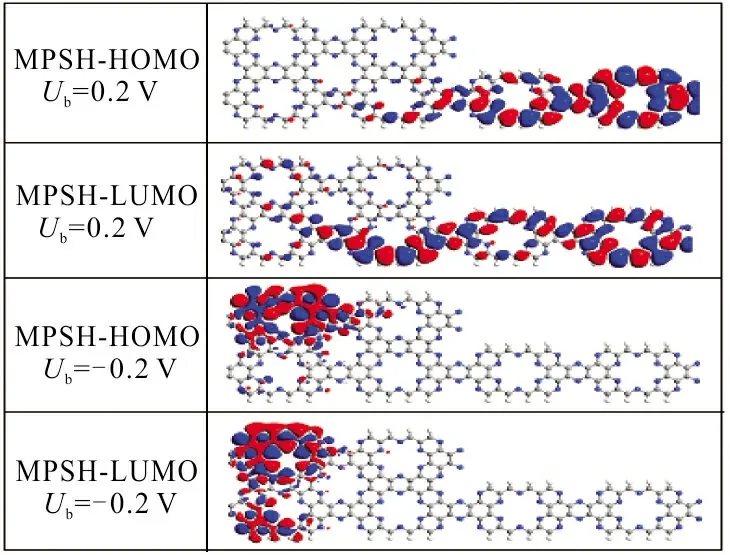
(e) Ub =±0.2 V时,M2的MPSH
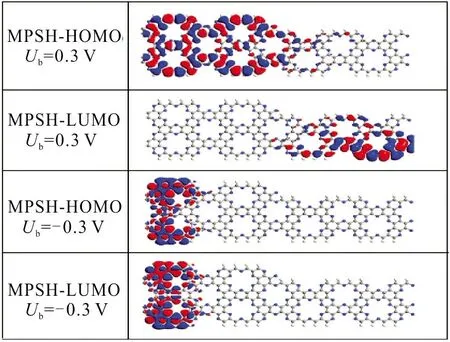
(f) Ub =±0.3 V时,M3的MPSH图 6 M1、M2和M3在各种偏压下的透射谱和MPSHFig.6 The transmission spectra and MPSH of M1,M2 and M3 at different biases
3 结 论
1) 非对称式结构会改善C2N-h2D纳米带的电输运机制。经计算,3组非对称式的纳米带均呈现出显著的NDR效应和整流特性。
2)WL∶WR=1.5∶1.0结构下的输运性能最优,其电流的峰谷比高达272.3。在Ub=0.2 V时,最大整流比为Rmax=17.824×103。
3) 当台阶加宽,带宽比为WL∶WR=2.0∶1.0和WL∶WR=2.0∶1.5时,电流值渐渐减小,整流比值降低。
4) 这些结果为设计和制备基于C2N-h2D纳米带的纳米级NDR器件和整流器件提供了一定的理论指导。
