证券市场中庄家与散户间的确定性微分博弈
2021-11-03潘素娟李时银赵佩
潘素娟, 李时银, 赵佩
( 1.福建商学院 信息工程学院, 福州 350012; 2.厦门大学 数学学院, 福建 厦门 361005 )
在现实的博弈决策中,由于时间是不间断的,因此博弈的参与者必须时刻作出决策.研究表明,可应用确定性微分博弈来分析连续时间的决策行为.例如: Dominika等[1]针对竞争细分市场给出了一种商誉模型的开环均衡解存在的充分条件; Zhou等[2]将Pontryagin最大值原理作为最优性条件,研究了参与者不断更新的合作微分对策; Puduru等[3]在事件树上给出了约束线性二次动态博弈的反馈和开环纳什均衡解;程粟粟等[4]利用动态博弈的方法研究发现,在战略合作下博弈参与国捕获和封存的二氧化碳数量最多; Abraham等[5]根据广义纳什博弈理论,给出了在离散时间动态博弈(DTDG)中存在开环纳什均衡条件的一种新的求解方法.众所周知,在证券市场中庄家和散户的博弈对证券市场的走势具有重要的影响.但目前为止,尚未见到将确定性微分博弈理论应用于庄家和散户间的连续时间博弈的研究中.为此,本研究运用动态博弈理论中的确定性微分博弈对专家和散户之间的博弈行为进行分析,得到了庄家和散户博弈的开环纳什均衡策略和反馈纳什均衡策略.
1 微分博弈的动态系统
1.1 动态博弈理论
1) 假设在一个微分博弈中,每位参与者的目标函数为:
(1)
其中n为总人数,gi(·)≥0,φi(·)≥0.目标函数(1)的值取决于如下的确定性动态系统[6]:
(2)

2)将ηi(·) (i∈N)定义为一个集合函数,并表示为:
(3)
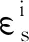

(4)
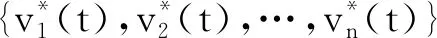

1.2 资讯结构的类型
1.2.1开环资讯结构(OLIS) 如果在博弈的开始时刻即可确定整个博弈过程的策略,则该资讯结构是开环的[9].开环资讯结构下每个参与者i的资讯结构为ηi(s)={x0},s∈[t0,T].参与者的策略是由当前时间点s和开始状态所决定的,即{ui(s)=ψi(s,x0),∀i∈N}.由上述可知,开环资讯结构存在一旦选定策略就无法做出改变的局限.
1.2.2闭环完美状态(CLPS) 如果每个参与者的策略是由开始到当前的状态和时间确定的,则可将该资讯结构视为闭环完美状态.闭环完美状态下参与者在博弈的过程中所采用的策略为ηi(s)={x(t),t0≤t≤s}, 现实中大部分的资讯结构都属于这一类.
1.2.3无记忆完美状态(MPS) 如果每位参与者的策略都是由开始状态、当前时间和当前状态所决定,则可将该资讯结构视为无记忆完美状态[10].无记忆完美状态下每个参与者i的资讯结构为ηi(s)={x0,x(s)},s∈[t0,T].此时参与者的策略是当前时间点s、开始状态x0和当前状态x(s)的函数,即{ui(s)=ψi(s,x(s)x0),∀i∈N}.在无记忆完美状态下,参与者的策略与过去的资讯(开始时刻除外)无关,只与开始时刻和当前的资讯有关.
2 证券市场的微分博弈
2.1 庄家与散户间博弈的模型假设
1)将股票市场中的散户投资者作为一个整体与庄家进行博弈,即博弈参与双方为庄家和散户.
2)庄家和散户均为理性人,每个博弈参与者都能对自己和其他人的行为有正确的预期.庄家和散户在采取任何策略之前,都会考虑截至目前的历史股价走势,并预期自己的行为对随后决策所造成的影响.
3)博弈的结构和完全理性对每个参与者而言都是常识,博弈中一方的增持必然意味着另一方的减持.
4)庄家和散户间的博弈信息是不完全和非对称性的.由于庄家能够密切了解上市公司的动态和宏观政策的变化,所以在预测股票价格的变动时,庄家通常比散户具有更及时、准确的信息.
2.2 证券市场微分博弈的动态系统
由于庄家和散户都希望最大化一段时间内的投资回报,因此庄家和散户的目标函数可分别表达为:
(5)
(6)
其中:T表示庄家在这只股票上的持股时间;状态x(t)表示庄家在时间点t的持股率,即该股票在时间点t的庄家控盘系数; 1-x(t)为散户投资者在时间点t的持股率;qi表示持股率对投资者i收益的短期边际影响,即股票瞬时收益率;ci是交易成本率;r为贴现利率;Si是持股结束时持股率对股票收益的边际影响;ui(t)为t期庄家或散户净买卖股票的数量;ui(t)>0表示净买进的股票数量;ui(t)<0表示净卖出的股票数量;r、qi、ci和Si对于i∈{1,2}都是正常数.
在庄家的决策中,假设每个时间点的净买卖股票数量就是庄家的策略空间,由此庄家持股率的变化(博弈的动态系统)可表示为
(7)
将式(5)—(7)联立即可构成庄家与散户间的确定性微分博弈模型.庄家和散户根据当前时间和持股率决定最优策略.在每个时间点t, 如果一方的净买卖股票数量已经确定,则另一方在确定最优策略时,不仅需要考虑持股率变化对自己在当前时刻的瞬时支付(收益)的影响,还要考虑持股率变化对将来收益的各种影响.
3 确定性微分博弈的求解过程
应用开环纳什均衡和反馈纳什均衡的方法即可求解由公式(5)—(7)联立所构成的确定性微分博弈模型.
3.1 专家和散户的开环纳什均衡解
根据开环纳什均衡的解法,对上述确定性微分博弈模型进行求解可得如下定理1:
定理1在确定性微分博弈中,庄家和散户的开环纳什均衡策略为:
(8)
其中A1(t)和A2(t)的值不仅取决于市场利率、交易成本、持股率对投资收益的短期和长期边际影响,而且还受到A1(t)和A2(t)的互动影响.A1(t)和A2(t)依赖如下的动态系统和边际条件:
A1(T)=S1,A2(T)=-S2
(9)
证明由于定理1的证明属于标准最优控制问题,因此可用Pontryagin的最大化原理[11]来证明.根据开环纳什均衡解法可得:
Λ1(T)=exp(-rT)S1,Λ2(T)=-exp(-rT)S2.
(10)
由式(10)可知,庄家和散户根据各自的持股率和交易成本,在保证理性的最优化收益的情况下,其在每个时间点净买卖的股票数量分别为:
(11)

(12)
Λ1(T)=S1exp(-rT),Λ2(T)=-S2exp(-rT).
(13)
求解式(12)和式(13)所组成的微分方程组可得
Λ1(t)=A1(t)exp(-rt),Λ2(t)=A2(t)exp(-rt).
(14)
将式(14)代入式(11)即可证得定理1.
由上述开环纳什均衡策略可以得到以下结论:
1)在最初开始时刻,最优状态与博弈的开始状态相同,而最优状态在当前的变化取决于当前的状态、时间以及专家和散户的最优策略;
2)如果专家和散户中的一方采用自己的最优策略,则另一方在选择最优策略时,除了要考虑自己在当前状态的瞬时支付,还要考虑自己在未来状态的所有支付;
3)假设专家和散户都采用自己的最优策略,且他们的最优策略都只依赖于开始状态和当前时间,则专家和散户的共态函数就可以反映出最优状态给他们的未来支付所带来的影响.
3.2 专家和散户的反馈纳什均衡解
为了避免在推导纳什均衡时能够碰到资讯非唯一性的问题,本文假设专家和散户的资讯结构都为无记忆完美状态(MPS)或闭环完美状态(CLPS).根据反馈纳什均衡解法,对上述确定性微分博弈模型进行求解可得如下定理2:
定理2在连续时间下,庄家和散户在确定性微分博弈中的反馈纳什均衡策略为:
(15)
证明根据Bellman的动态规划,微分博弈的反馈纳什均衡解应满足以下Issacs - Bellman偏微分方程组:
V1(T,x)=exp(-rT)S1x,V2(T,x)=exp(-rT)S2(1-x).
(16)
其中Vi(t,x)是参与者i的价值函数,Vi t(t,x)、Vi x(t,x)分别是Vi(t,x)对t和x的一阶偏导.
1)求解公式(4)—(9)中的最大值,由此得到如下最优策略:
(17)
V1(T,x)=exp(-rT)S1x,V2(T,x)=exp(-rT)S2(1-x).
(18)
3)求解方程组(18),得如下庄家和散户的价值函数:
V1(t,x)=exp(-rt)[A1(t)x+B1(t)],V2(t,x)=exp(-rt)[A2(t)(1-x)+B2(t)].(19)
其中:A1(t)和A2(t)的值不仅取决于市场利率、交易成本、持股率对投资收益的短期和长期的边际影响,而且还受A1(t)和A2(t)互动的影响;而B1(t)和B2(t)的值不仅取决于市场利率和交易成本,还取决于A1(t)和A2(t)的值.A1(t)、A2(t)、B1(t)和B2(t)依赖如下动态系统:
(20)
A1(t)、A2(t)、B1(t)和B2(t)的边际条件为:
A1(T)=S1,B1(T)=0,A2(T)=S2,B2(T)=0.
(21)
4)用式(19)中的价值函数V1(t,x)和V2(t,x)分别对x求偏导,将所得结果代入式(17)即可求得庄家和散户的反馈纳什均衡策略.
由上述反馈纳什均衡策略可知,庄家和散户根据当前状态和时间选定最优策略时,专家和散户的价值函数将随着时间的改变而改变,其中价值函数在每一瞬间的改变量相当于状态的最优变化为价值函数所带来的转变与它的瞬时支付之和.另外,庄家和散户在最后时间点T时的支付(收益)等于其在博弈的终点支付.
4 结论
本文利用动态博弈的方法和多种资讯结构类型,针对证券市场建立了一种庄家与散户在证券市场中的确定性微分博弈模型,并分别运用开环纳什均衡和反馈纳什均衡的方法求解出了博弈双方较为完美的反馈纳什均衡策略和开环纳什均衡策略.本文研究结果可以为金融监管部门监管证券市场和证券市场投资者买卖股票提供参考.本文在研究过程中未能考虑到随机因素对博弈模型的影响,因此在今后的研究中我们将用随机微分方程理论描述国内外机构投资者和散户群体所参与的博弈,以此进一步提高本文模型的适用性.
