基于维修大数据的飞机结构故障预测

田家豪， 宋庭新

(湖北工业大学机械工程学院， 湖北 武汉 430068)

早在1990年代，国外航空领域就提出了故障预测与健康管理系统(PHM)的概念。在欧美航空技术发达国家，PHM技术已经得到了行业及研究机构的充分肯定，正朝着更加全面、标准化、智能化的方向发展。PHM技术在美国的联合攻击战斗机(JSF)项目首次得到实际应用。开发这个项目是为了提高JSF的飞行安全性，显著降低作战和保障成本，并将飞机兵团老化的的影响降到最低[1]。英国将PHM技术开发成发动机健康管理系统，以监测其性能并提供维护趋势信息[2]。目前，国内对于飞机结构故障的预测研究已有报道，但基于数据驱动的故障预测方法在飞机维修方面的应用才刚刚开始。沈阳飞机设计研究所在飞机PHM系统设计方面开展了大量的理论与方法研究，设计并验证了一种数据驱动视角下飞机PHM系统[3]。空军工程大学张凤鸣等人对现有机载PHM系统方案进行了总结，提出了一种层次化、集成化的机载PHM体系结构，并对其结构、信息传输和外部逻辑接口等功能进行了描述[4]。虽然我国在飞机维修与结构故障预测方面获得了一定的进展，但与发达国家相比，整体性上还存在一些问题，需要继续加强研究。

本文针对某型飞机维修数据，采用Fisher判别法和ARIMA时间序列模型，对飞机结构故障进行预测，解决了传统的故障诊断推理方法难以充分使用大量数据实现飞机维修保障的问题。

1 数据挖掘算法和故障预测模型

目前飞机的维护维修手段主要通过定期检查或是事故发生之后再进行维修。这种被动的维护维修手段不仅效率低下、维护成本高，而且无法利用系统现状和历史数据预测未来状况，一旦出现故障，很有可能引起坠机等毁灭性事故。现代飞机的系统结构复杂，单一的解析模型无法对故障进行确切分析，不能满足飞机的健康管理需求。因此对大量维修数据的潜在价值进行深度挖掘为飞机结构故障预测给出了新的解决方案。目前使用的数据挖掘方法主要包括聚类分析、判别分析、关联分析和预测分析等，针对的是各种不同的预测分析需求。考虑到飞机结构故障的实际预测需求，本文选取Fisher判别法对故障发生位置进行预测，使用ARMA模型对故障发生时间进行预测。

1.1 Fisher判别法

Fisher判别法的理论基础为通过把高维度的数据点在低维度进行投影，在低维度得到更聚焦的数据点。假设输入序列为x，组数是i，指标数是p，系数向量为C，可得到通过方差分析法求出的判别函数

(1)

式中，当组内相差最小且组间相差最大时，可以确定参数ci。对标准化数据进行分类预测时，把p个指标逐个代入式(1)求出Fi值，然后将待分类数据分到最大值对应的组，从而判别数据类别即故障位置。与其他判别分析方法对比，Fisher判别分析方法的应用范围广，限制条件少，不需要较多的先验信息，更适用于飞机维修数据这种分布较散的情况。

1.2 时间序列ARMA模型

ARMA模型的理论基础是对历史数据序列的信息进行统计分析，根据统计得到的数据序列的相关关系来确定序列值之间的相关规律，拟合出可以描述这种关系的模型，并且使用模型分析预测序列之后时间的状况。

ARMA模型利用系统过去若干个时刻的状态以及过去若干个时刻噪声项进行线性组合，来对当前的状态做出估计和预测。将白噪声序列at输入线性的系统，输出为平稳序列xt，ARMA模型专门用于描述这种输入与输出之间的规律，即

xt=φ1xt-1+φ2xt-2+…+φpxt-p+at-θ1at-1-…-θqat-q

(2)

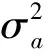
ARMA模型还需要参数估计。相比于AR模型，ARMA模型的参数估计较为复杂，由于同时涉及AR模型参数和MA模型参数，且二者的自相关正则方程是不同性质的，通常采用三步近似的方法来实现。

2 飞机结构故障预测方法

本文以某型飞机的故障和维修记录为例，在充分收集该飞机的各种数据和维修记录的基础上，使用Fisher判别法和ARMA模型，拟合出能够预测飞机结构故障的算法模型，找到飞机结构故障和维修数据之间的影响关系。

2.1 维修数据的预处理与标准化

飞机具有较为复杂的下级系统分类，在查询相关标准的基础上，将飞机分为控制系统、燃油系统、液压系统、电气系统、气压系统、环境控制系统、应急系统、旋转翼系统和其他系统，通过分类分析可以确定故障件所属的具体系统。目前飞机的维修记录大多根据维修人员的经验记录为描述性语句，因此无法直接对维修记录进行拟合处理，需要对维修记录进行量化分析和预处理(即标准化)。首先，选择影响故障分布的指标。在分析飞机结构故障的维修记录时发现，与故障分布相关的数据众多，从中可以择取相关的因变量。分析维修数据后，本文选出9个对飞机故障预测产生影响的变量(故障时间、飞机修后工作时间、故障件修后时间、故障件翻修次数、换上件工作时间、发现时机、专业、故障部位和故障责任)。其次，将数据标准化。对飞机维修数据进行标准化处理需要制定规则，用量化指标代表部分非结构化数据，为后面的大数据分析处理平台提供有效数据源。除开故障件翻修次数直接使用数值，其余各类时间时次运用区间分类，自然语言表述赋予对应值进行区分。本文编写Python脚本语言对飞机质控数据和故障记录进行扫描，提取出选定的指标信息，根据数据统计结果，对出现的自然语言描述进行赋值，标准化结果如表1所示。

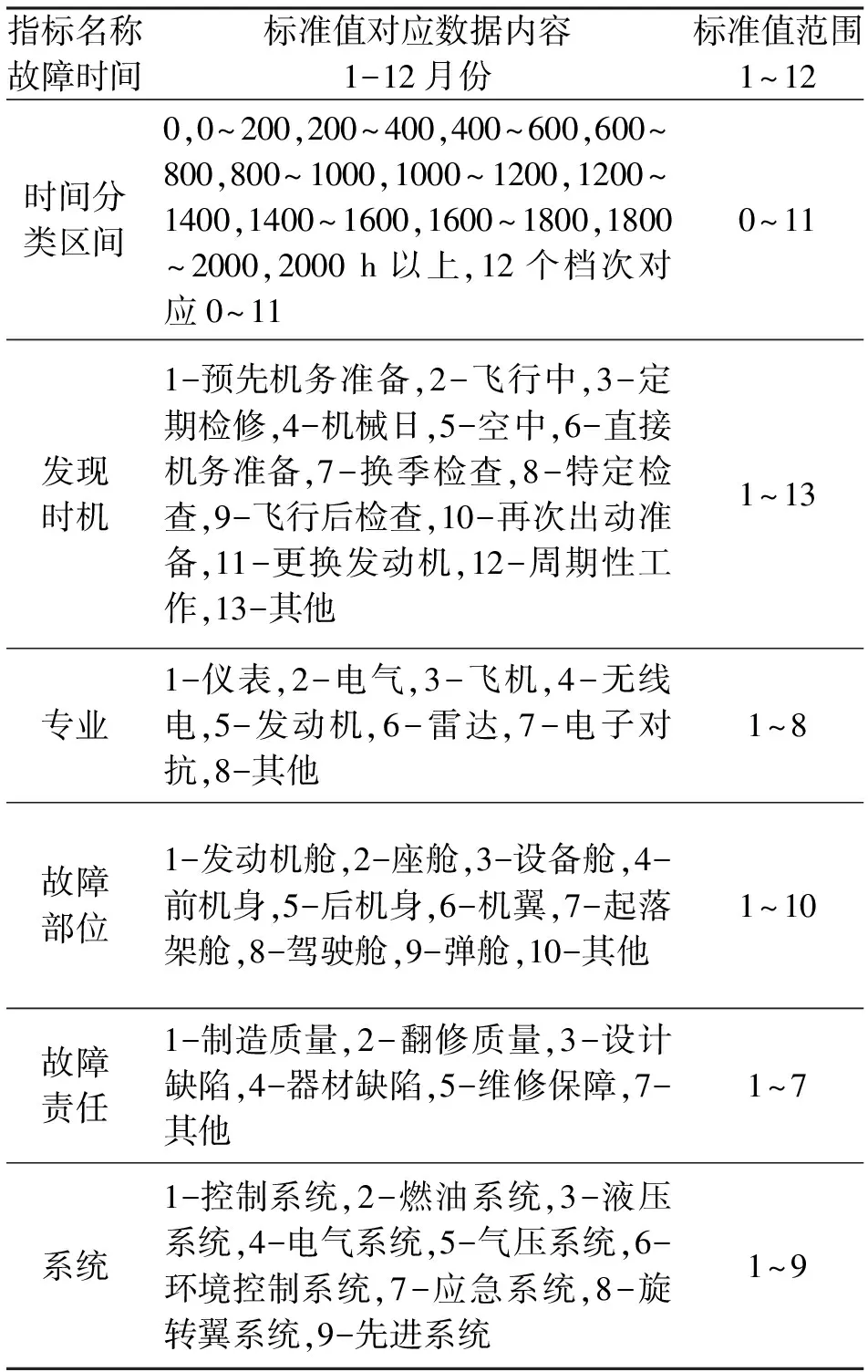
表1 数据标准化结果

在初步制定的量化指标基础上，编写Python脚本语言对维修数据进行大规模清洗，将数据标准化，为后续分析预测做准备。

2.2 基于Fisher判别法的故障预测模型

2.2.1影响指标筛选影响飞机故障的指标很多，需要借助分析方法对一些不重要的指标进行排除，拟合出更为简约的模型以节省算力。通过数据预处理程序计算得到组平均值的同等检验表(表2)。表2中统计量的含义如下：威尔克Lambda表示相应因素对模型的影响，其数值越小，影响越大，取值范围为0～1；F表示模型的适应性，即是否适合分析影响指标，F值越大，模型越合适；自由度，自由度1+自由度2=N，其中N是训练样本数量。

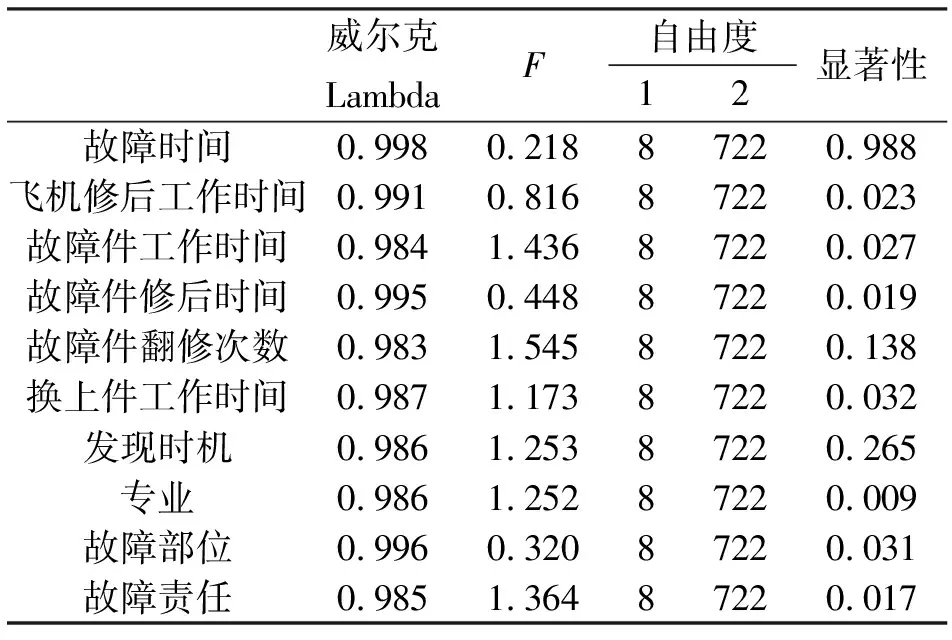
表2 组平均值的同等检验表

通过分析表2中显著性指标的值能够对影响指标进行初步筛选。从表2中可见，故障时间、故障件翻修次数、发现时机的显著性超过了0.05，若以0.05作为显著水平的标准分界(此时能够解释方差99.8%的比例)，说明三者的均值不存在显著性差异，在后续的分析预测中可予以排除。

为验证标准化处理后的数据集适合Fisher判别法进行分类，把筛选过的数据输入到SPSS中，得到典则判别函数摘要，如表3、4所示的分析结果。

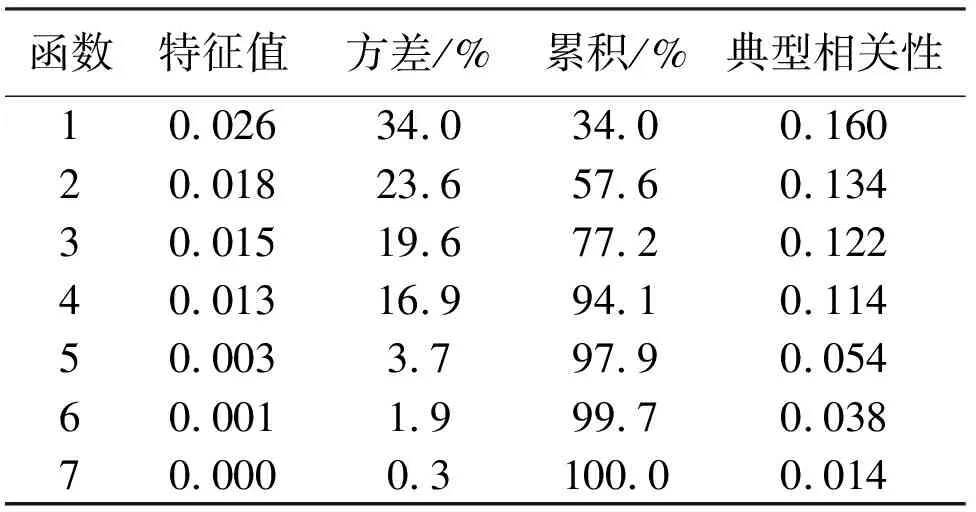
表3 特征值

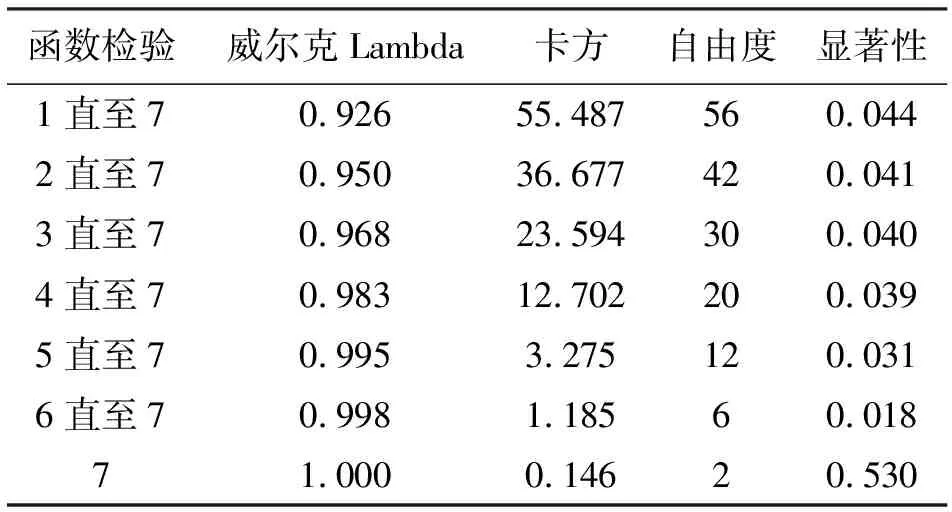
表4 Wilks Lambda

从表3、表4可以看出，数据集可以通过7个Fisher典型判别函数来完成分类。前6组函数检验的显著性均小于0.05，这代表着他们在0.05显著水平上存在显著差异，对于数据集的分类有明显积极作用。根据检验结果可以说明Fisher判别法适用于对当前数据集的分组，能够进行下一步的建模分析。

2.2.2系统分组模型的建立Fisher判别法是一种求组间差异最大且组内离差平方和最小的线性判别函数。其中多组Fisher判别函数系数的求解方法为[5]：设有k组G1，G2，…，Gk，它的均值和协方差矩阵为μ1,μ2,…,μk和∑1,∑2,…，∑k，从组中提取有p个指标的样本，在方差分析的基础上建立的判别函数

C(Y)=C1Y1+C2Y2+…+CpYp=C′Y

(3)

其中，系数C1，C2，…，Cp确定的前提是组间差最大，且组内差最小。

在上述算法的基础上，使用聚类分析功能对模型进行拟合训练，输入训练样本数据进行分析得到分类函数系数如表5所示。

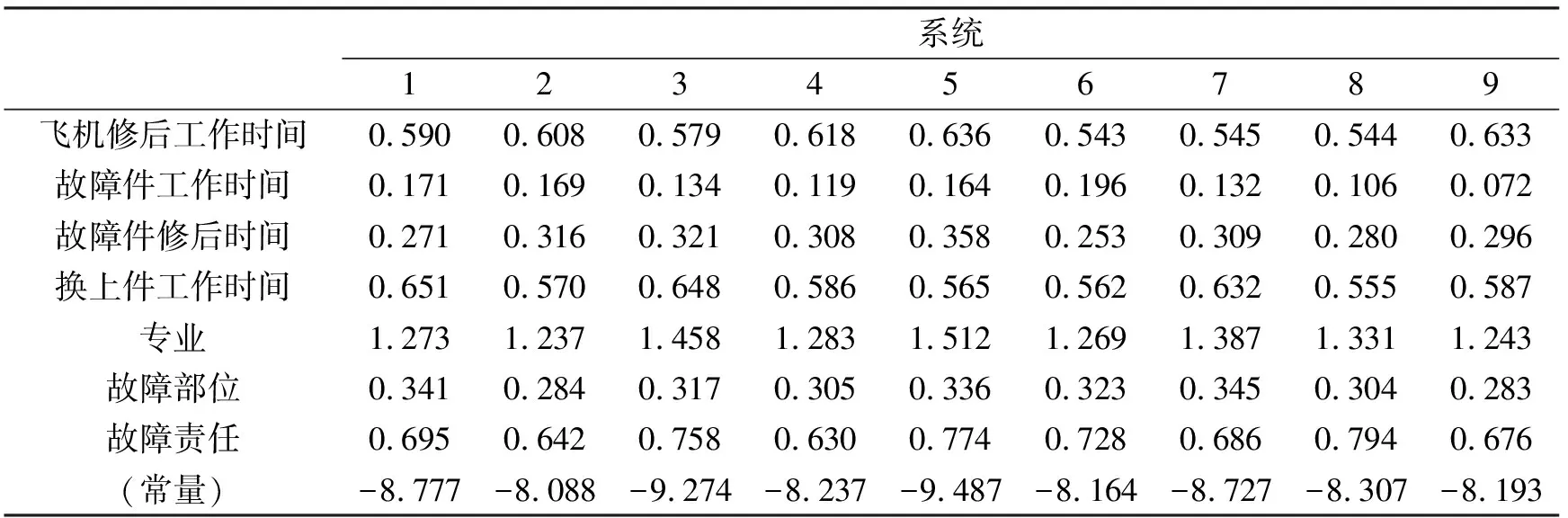
表5 分类函数系数

由表5可得9个系统判别函数为：

F1=0.59x1+0.171x2+0.271x3+0.651x4+ 1.273x5+0.341x6+0.695x7-8.777F2=0.608x1+0.169x2+0.316x3+0.57x4+ 1.237x5+0.284x6+0.642x7-8.088F3=0.579x1+0.134x2+0.321x3+0.648x4+ 1.458x5+0.317x6+0.758x7-9.274F4=0.618x1+0.119x2+0.308x3+0.586x4+ 1.283x5+0.305x6+0.63x7-8.237F5=0.636x1+0.164x2+0.358x3+0.565x4+ 1.512x5+0.336x6+0.774x7-9.487F6=0.543x1+0.196x2+0.253x3+0.562x4+ 1.269x5+0.323x6+0.728x7-8.164F7=0.545x1+0.132x2+0.309x3+0.632x4+ 1.387x5+0.345x6+0.686x7-8.727F8=0.544x1+0.106x2+0.28x3+0.555x4+ 1.331x5+0.304x6+0.794x7-8.307F9=0.633x1+0.072x2+0.296x3+0.587x4+ 1.243x5+0.283x6+0.676x7-8.193

其中：x1为飞机修后工作时间；x2为故障件工作时间；x3为故障件修后时间；x4为换上件工作时间；x5为专业；x6为故障部位；x7为故障责任。

根据上述分类方法，在数据集中抽出一条维修数据进行验证分析。该故障的飞机修后工作时间为346.65 h，故障件工作时间为707.34 h，故障件修后时间为131.26 h，换上件工作时间为647.56 h，专业为仪表，故障部位为座舱，故障责任为制造质量。将上述维修数据进行标准化处理，得到表6参数。将参数带入判别函数组，计算出各组函数值(表7)。

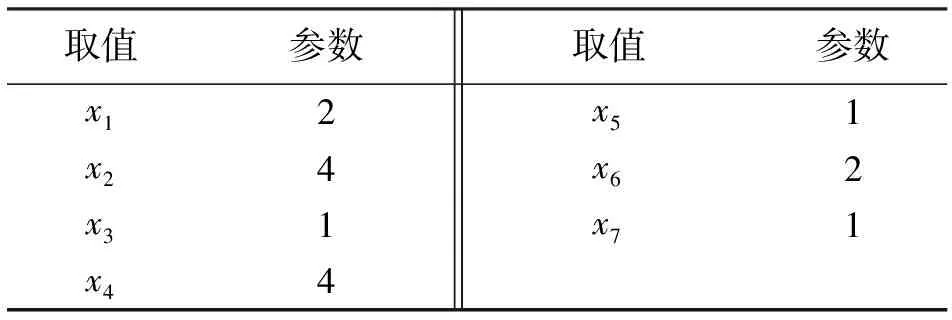
表6 参数取值

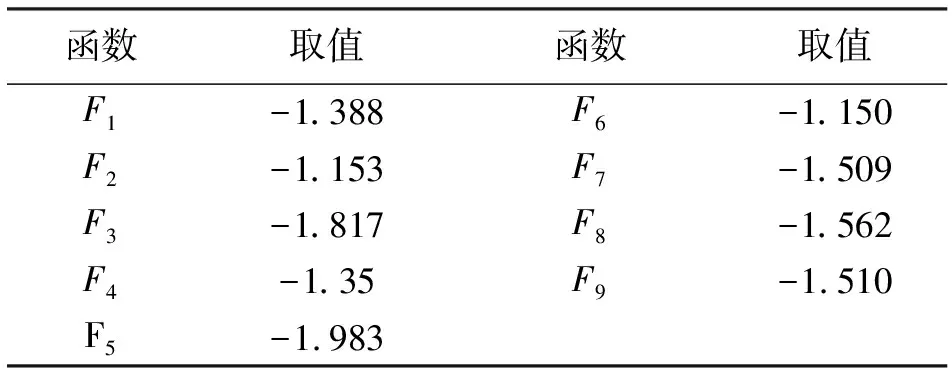
表7 函数取值

根据Fisher判别法的判别标准，发现在9个F值中F6最大，说明经过分析，该故障属于系统6，即该故障最可能出现在6-环境控制系统。

依据上述算法，将飞机质控系统中导出的维修数据代入进行预测分析，3次随机选取100组预测结果进行分析，准确率约为43.2%。编写接口再将预测后的数据加入训练样本进行反复训练，在训练样本条数14372条的情况下，三次随机选取100组预测结果进行分析发现，准确率约为65.4%。通过与某型飞机的实际维修记录进行对比，发现Fisher结构故障系统分类预测模型对于故障位置预测的正确率可达到70%以上，而在相同情况下，采用传统的多元线性回归预测模型是41.7%。研究发现，样本数据越多，正确率越高，说明在分析处理海量数据时，Fisher结构故障系统分类预测模型的正确率更高，效果更好。

3 基于ARIMA模型的故障时间预测

Fisher判别法实现了对飞机故障发生的系统或位置的预测，但对于故障发生时间和次数的预测则采用ARIMA模型更为合适。

3.1 数据的预处理

选用某型飞机2000年1月至2018年12月之间的维修数据作为数据来源。数据源中共有机型、飞机编号、故障日期、故障件名称等属性65个。将该数据作为训练集，需要对数据进行预处理。首先除去季节性异常值，使用插值补充缺失值，通过数据平滑处理，得到飞机维修数据的时序(图3)。

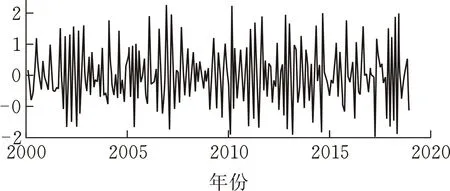
图 1 已处理数据时序

3.2 模型判断

就ARIMA模型来说，常见的有3种模型分支.为了选出适合的ARIMA模型，引入了序列的自相关图ACF和序列的偏相关图PACF。假设偏相关系数是p阶，自相关系数为q阶，在自相关系数拖尾时，应该选用p阶段截尾的AR(p)模型；在偏相关系数拖尾时，应该选用q阶截尾的ARMA(q)模型；如果自相关系数和偏相关系数都出现拖尾，则应选用ARMA(q，p)模型[6]。在选定模型的基础上，对模型的适用性进行验证。本文对预测模型输出的残差进行分析，发现其满足均值为0的正态分布，说明在滞后阶数无论为何值的情况下，残差的自相关系数均为0，即拟合的模型适合对该数据集进行预测分析。

函数计算选定ARIMA模型的参数为p=2、d=l和q=1。使用R语言编程，将参数输入ARIMA模型，能够在可视化界面得到预测图(图6)。

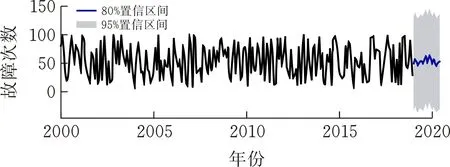
图 2 月故障次数预测

经过多次试验，发现预测结果对于数据处理要求较高，如果出现错误或噪声数据过多，预测结果也会出现明显的偏差，需要足够的数据量进行训练，才能得出可靠的预测结果。

4 结束语

本文以飞机结构故障预测为目标，充分利用维修大数据进行分析研究，采用基于Fisher判别的量化分析方法和基于时间序列分析的ARIMA模型，对飞机结构故障位置和故障发生的时间次数进行了预测。研究结果对飞机维修数据记录不准确而迫切需要降低飞机结构损伤的矛盾给予了行之有效的解决方法，即将维修数据进行量化处理，使用容易理解和应用的算法和预测模型。实验证明，基于大数据分析的Fisher结构故障系统分类预测模型和时间序列ARIMA模型对于故障发生位置和故障发生时间的预测准确率可达到70%以上。对于飞机结构故障的准确预测，会大大降低飞机安全事故，降低维修成本，避免飞机由于结构故障原因而造成不必要的损失。