基于大数据分析和多模型融合的交通拥堵高效预测技术
2021-11-02林立春洪东刘华
林立春 洪东 刘华


文章利用可变系数加权优化方法对交通大数据进行聚类分析,并为了适用于常发性和偶发性拥堵,采用改进的两级加权优化ELM对分类进行模式识别,以期提高拥堵预测的精确度。同时,引入了上下游关联的拥堵传导模型,进一步提高拥堵预测的关联性。当预测到或已检测到交通拥堵时,在拥堵诱导上采用路网局部最优化模型为出行者规划路线,路网全局最优化模型则为管理部门使用并为未来规划提供辅助决策。仿真实验结果表明,多模型融合技术能预测较长时间后的拥堵情况并维持较高的准确率,为构建高效、经济、安全和便捷的现代化综合交通体系提供科技支撑。
大数据;交通拥堵;预测;多模型;拥堵传导
U491.1+13A421515
0 引言
伴随着我国人民生活水平的稳步提高和社会的快速发展,机动车保有量迅速增加,居民出行总量提高,交通拥堵问题越来越严重,成为影响和制约城市发展以及饱受民众诟病的热点。在现今“互联网+”和大数据发展的时代,利用大数据分析以及合适的技术,可以科学地预测道路的拥堵程度,为出行合理规划路线,提高出行效率,减少安全事故隐患,降低城市排放污染,释放城市发展潜能。本文的重点在于拥堵的预测,创新贡献点主要有:(1)可变系数加权聚类优化模型;(2)两级加权并自适应权重模型以全面应对常发性和偶发性拥堵;(3)将两级加权与极限学习机(下称ELM)结合,使其既保持快速又能适用于平衡数据集和不平衡数据集,达到快速与准确并存;(4)采用拥堵传导模型,考虑上下游情况,进而能够从全局角度观察,辅助管理决策;(5)预测到拥堵后采用路网总成本最优化模型实现交通诱导,以提高城市的整体通行能力。
1 架构的提出
交通拥堵从成因上来划分一般可归纳为常发性交通拥堵和偶发性交通拥堵。详见文献[1]。常发性交通拥堵具有一定规律可循,大数据分析上具有明显特征。而诸如交通事故、交通违法、道路施工、极端天气、大型活动、特殊路段等动态因素影响而发生的偶发性交通拥堵随机性大,规律不甚明显。为此,本文提出建立含有常发性和偶发性拥堵规则库及动态影响数据库,当偶发性拥堵发生时,通过两级加权优化模型侧重于偶发性拥堵规则,常发性拥堵规则只做辅助参考,并通过预测时刻到来时的实时数据的验证对加权进行自学习(自适应),以期收敛和准确,同时丰富规则库。当无偶发性拥堵因素时,则以常发性拥堵规则为主。
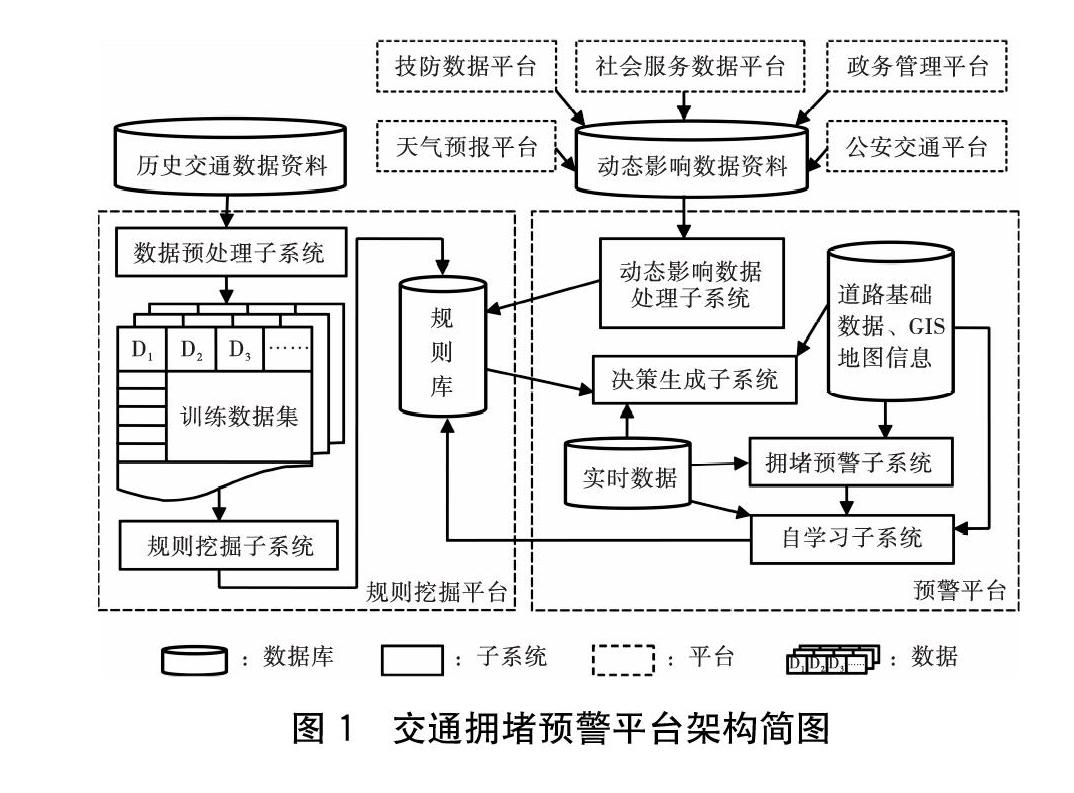
为此,提出基于大数据分析的多模型融合(Big Data Analytics with Multiple Mode Combination,BDA-MMC)交通拥堵预警平台,其架构简图如图1所示。架构的核心是融合多种模型来构建规则库,其优劣直接关系到预测精度。
2 关键技术
2.1 可变系数加权聚类优化模型
模糊C均值聚类(FCM)不同于传统的K均值聚类(K-means),它是一种柔性划分方法,划分结果是各个样本的隶属程度,而不是属于某类,正符合拥堵程度的划分需求。
但各路段本质特征又有区别,如车道数量、人行横道数量、红绿灯数量和占有率等,加之工作日、周末和节假日之间的数据特征也有一定差异,显然需要对不同维度上的特征予以区分。本文在FCM基础上提出了一种可变系数加权聚类优化模型及权重自学习方法。
令W={W1,W2,……,Wn}为n维特征的对应权值集合,定义第i个维度特征的可变系数为:
Vi=σiμi(1)
式中:μi=1n∑nj=1χij,σi=1n∑nj=1(χij-μi)2。再为第i维特征的可变系数加权:
Wi=Vi∑nj=1Vj
(2)
通过可变系数加权值求得对象xi到聚类中心vk的距离dki:
dki=∑nj=1Wj(xij-vkj)2
(3)
对应的隶属度计算公式为:
uij=∑Kk=1∑nhWh(xjh-vih)2∑nhWh(xjh-vkh)1m-1-1(4)
計算权重的修正量公式为:
ΔWi=-ηE(W)Wi(5)
式中:E(W)——极小评价函数;
η——学习率。
η通过下面公式计算:
EW1-ηE(W)W1,…,Wm-ηE(W)Wn=
minλ>0EW1-λE(W)W1,…,Wn-ηE(W)Wm(6)
当Wi+ΔWi>0时,更新权重Wi=Wi+ΔWi。
2.2 两级加权优化的ELM及自适应权重模型
通过聚类将大数据划分为若干类之后,另一关键技术就是分类识别获得与预测时段最相似的样本集和规则。极限学习机(Extreme Learning Machine,ELM)在处理大数据问题时以快速著称,适用于拟合、分类和模式识别等问题[5]。但缺点是当有“噪声”——数据集里存在离群点时,性能会受到影响。为弥补这一缺点,本文对ELM进行改进,进行两级加权优化。因为偶发性拥堵相对于历年的海量常发性拥堵来说占比极小,相当于噪声,但在现实中却无疑会引发拥堵,只是程度不同而已。故此,当偶发性拥堵发生时,不仅不应让这些少数类被淹没,还要加大其权重,以期ELM在快速(时效性)的基础上又能提高预测准确度,还能使其同时适用于平衡和不平衡的大数据集合。
参考文献[4],给定预测样本xi,训练好的N个学习机的预测输出为f1(xi),…,fn(xi),…,fN(xi),其中fn(xi)=[f1n(xi),f2n(xi),…,fMn(xi)]T。首先进行一级加权优化,方法是计算每个学习机各个节点的概率输出,公式如下:
pmn(fmn(xi))=11+exp(-(fmn(xi))),m=1,2,…,M,n=1,2,…,N(7)
进一步对其归一化得到:
pmn(xi)=p(fmn(xi))∑Mt=1p(ftn(xi)),m=1,2,…,M,n=1,2,…,N(8)
再确定每个学习机概率输出的最大值:
pn=maxm=1,2,…,M{pmn(xi)}(9)
pn越大,该分类器在多模融合预测中的权值也应越大,一级加权定义为:
un=pn∑Nn=1pn(10)
最后进行二级加权wδ,计算样本xi在预测模型中的输出:
class(xi)=argmaxm=1,2,…,M∑Nn=1wδunpmn(xi)(11)
二级加权wδ取值范围为[0,1],在常发性拥堵——无动态影响因素时初始化为:
wδ=10.618Num(xi)>AVG(Num(xi))Num(xi)≤AVG(Num(xi))(12)
Num(xi)是指属于xi类的样本数目,当其大于平均数目时,既侧重于多数类,并有效抑制噪声。在偶发性拥堵时,wδ的取值则反过来,侧重于少数类。wδ以线性回归模型为基础,通过自学习动态在[0,1]之间改变。在t时刻预测t+1时刻拥堵程度,当到达t+1时刻,根据浮动车实时采集的数据来验证,通过验证的偏差来调整权重,以期准确和收敛。当该规则有效,则加入规则库。这种自适应权重既保持ELM的快速,还在一定程度上防止过拟合,且能提高模型的自适应能力,亦能克服普通的线性回归不能很好地反映交通的非线性变化和不确定性的缺点。
2.3 拥堵传导模型(上下游关联规则模型)
为了提高较长时长后的预测拥堵的准确性,还要考虑拥堵的上下游关联传导关系。因为交通拥堵的产生在时间上和空间上都是一个较复杂的过程。本文的拥堵传导模型既考虑路段在路网空间拓扑上的邻接关系,也考虑拥堵状态的传导在时间上的先后关系。
如图2所示,当前RC路段箭头所示为行驶方向(另一方向同理),如果RC发生拥堵,一般会引发上游的i1~i3在Δt时间后发生拥堵。这在大数据分析中较容易通过RC的拥堵程度和i1~i3的流量预测出Δt,这里不赘述。
反过来,当上下游路段发生不同程度的拥堵后,何时会传导引发RC发生拥堵,这样的因果关联性是本文研究的重点。为降低时空复杂度,本平台拥堵传导模型仅计算直接拥堵传导(临边),但整个路网的连通性已能反映出间接拥堵传导(相隔路段之间传导)。
对于RC,关联模型主要考虑上游三个流入路段的流量Q(vehs/h),即流入RC的量;还有下游三个流出路段的平均行驶速度V(km/h),即RC的排出速度。当采用路段平均速度为交通拥堵指数时,平均速度即是拥堵程度。若再简化模型,把上游的流量也改为拥堵程度时,虽然计算简化,但在实际应用中的预测精度有所下降。
首先,通过道路方向与车辆行驶方向之间夹角过滤掉无关方向的浮动车,再通过检测器得到上游三个驶入流量Qi,i=1,2,3,下游三个驶出路段的平均行驶速度为Vj,j=1,2,3。拥堵传导预测计算公式如下:
α∑ni=1(αiQi)-β∑mj=1(βjVj)+γVRc(13)
式中:n——上游临边数;
m——下游临边数。
如果是图2所示的十字路口,n和m都等于3,如果存在无关的单行线等限行路段方向应将其忽略。αi、βj为参数,根据拥堵程度和流量占比给出;
α,β,γ——影响因子;
VRc——RC自身当前的拥堵程度。
路段平均行驶速度定义为:
V=∑nk=1Lk∑nk=1(LkVk)(14)
Lk为该路段上第k条记录的行驶车辆所驶过的距离;Vk为其速度。
除了考虑偶发性因素外,在常发性拥堵中,如何较准确地预测从居民区和单位等地驶出的新汇入到道路上的车辆数——流量变数,是预测中的难题之一,也是能否较准确预测拥堵的关键因素之一。为提高较长一段时间后(例如超过20 min之后)的拥堵预测准确度,以时间序列上众路段拥堵传导模型的计算值为主,以大数据挖掘出的每天上下班高峰期的流量变数为辅进行调整。因为绝大多数人的上下班时间段是固定的,乃至周末出行均有一定规律可循,从大数据分析可以得出;其他变数可以通过交通事故上报平台、道路施工的市政平台、极端天气的天气预报平台、大型活动的社会服务平台等采集,这样即可实现预测较长时间后拥堵程度的高准确度。
2.4 路网总成本最优化模型
在出行路线选择上,出行者仅仅从自身考虑,往往选择路线最短、耗时最短路线或者主干道路线。在发出拥堵预警后,给出的优化路线要充分考虑城市路网整体最优均衡,即實现了一种交通诱导,充分利用次级道路,提高城市整体通行能力。平台在为出行者服务时,为提高时空效率采用局部最优方法,计算起点i到终点j的预选路径集合所覆盖的局部路网的总成本最小[6]。记起止(OD)点间路径集合为Pij={Pij(t):路网从点i到点j的第t条路径};M为其流量矩阵;L(Pij(t))为路径Pij(t)的长度;Cij(t)为Pij(t)的通行能力;Xij(t)为Pij(t)上待分配的交通量。则建立路网寻优模型:
min∑i≠j∑tXij(t)×L(Pij(t))(15)
s.t.∑tXij(t)=Mij
0≤Xij(t)≤Cij(t)
∑XklXij(t)Xij(t)≤Ckl,
最后一条约束表示多条路径都经过某kl路段,则流经重叠路段kl的交通量总和∑Xkl不超过kl段的通行能力。该模型同样适用于整体路网总成本最优(全局最优),为相应管理部门所用或对未来交通规划辅助决策。
3 仿真实验
实验在讯方大数据服务器(2个英特尔至强银牌4110-2.1 G-8 Core处理器,2×32G DDR4内存,2块1 200 GB SAS 12 Gb/s-10 K rpm硬盘,1块RAID卡)、客户端Windows 10计算机(处理器Intel Core i7-9700,内存16 G)上进行;实验软件使用Python 3.9;样本数据采用广西交通运输云数据中心和南宁市交警支队部分样本数据;测试路网为南宁市中心区域多条易拥堵路线,并选取了18:00有交通事故的情况;在8:00、12:00、18:00三个早中晚上下班高峰时段进行重点预测,并以当时的真实拥堵程度值进行验证。评价指标选取常用的平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE),将BDA-MMC与广义回归神经网络(GRNN)、ELM和支持向量机(SVM)等模型的预测性能进行比较,结果如表1所示。
从表1中可以看出,本文基于大数据分析和多种模型融合(BDA-MMC)的拥堵预测结果明显提高,且在18:00有交通事故的偶发性拥堵预测中结果稳定。
4 结语
本文介绍了交通拥堵预警的主要方法,对历史大数据进行可变系数加权优化聚类分析,在分类识别上,为综合考虑常发性和偶发性交通拥堵,提出两级加权优化ELM和自适应权重模型,同时引入上下游关联的拥堵传导模型,进一步提升预测的准确性和关联性。在拥堵诱导上采用局部最优模型,充分发挥各级道路的作用以提高城市的整体通行能力。通过仿真实验证明,多模融合技术的交通拥堵预测方法不仅能够给出短时拥堵预测,还能够给出长时拥堵预测,并且均能维持较高的准确率。
预测交通拥堵的作用和意义重大,可以提前预防,如同治未病思想,而不是已经发生了拥堵甚至造成了事故才去弥补损失。在如今节奏越来越快的城市生活当中,时间是最宝贵的,拥堵预警从节约时间、绿色环保、高效通行和提高管理水平的角度出发是必需的,是引领智能出行的关键,也是建设交通强国,助力交通科学治理的技术支撑和强有力的手段。
但是,由于历史和信息安全等因素的约束,公安交通网络一般与互联网等网络是隔离的,交通实时数据对外共享较困难。建议将交通系统数据中有必要对外开放又不涉及隐私和信息安全的数据进行映射,对外共享。可采取授权访问的方式进行管理,商业化的要合理收费。同时,应逐步推进行业间大数据接口的标准,形成如图1中所示各部门之间有关交通大数据的相互对接和信息共享,加快信息产业的升级,使之更好地服务于社会。
[1]林立春,刘 华,洪 东.基于大数据分析的交通拥堵预测技术[J].西部交通科技,2020(9):138-141.
[2]沈 晴.面向交通擁堵预测大数据的神经网络群组快速学习[D].北京:北京科技大学,2017.
[3]周辉宇.基于大数据规则挖掘的交通拥堵治理研究[J].统计与信息论坛,2017,32(5):96-101.
[4]邓万宇,郑庆华,陈 琳,等.神经网络极速学习方法研究[J].计算机学报,2010,33(2):279-287.
[5]Lichun Lin,Shi Tong.Automatic Spatial Annotation of Image Based on Object Recognition [J].Journal of Information and Computational Science,2013,10(18): 5 829-5 847.
[6]薛倚明.整体优化路网交通量分配的系统思想[J].运筹与管理,2000,9(2):79-83.
