MAP译码器的免归一化处理信息更新算法*
2021-11-02王璇,杜军
王 璇,杜 军
(1.南京信息职业技术学院 电子信息学院,南京 210023;2.中兴光电子技术有限公司,南京 210012)
0 引 言
数据传输的可靠性是无线通信系统设计中一个非常重要的指标。Turbo编码[1]可以获得逼近香农信道容量的译码性能。Turbo码的解码[2-3]通常以迭代方式完成,一个译码器处理过的信息被迭代地馈送到另一个译码器,直到达到一定程度的收敛为止。
译码器中实现解码有各种各样的方法,其中基于BCJR(Bahl,Cocke,Jelinek and Raviv)算法的最大后验概率(Maximum A Posteriori Probability,MAP)译码算法[4]被广泛采用。MAP算法的目的是使得输出正确码字的概率最大化,包括系统信息和外信息的概率。在进行下一次迭代期间,其他译码器会用到外信息。这种算法采用的是迭代的译码过程,外信息在两个分量译码器之间进行迭代,以逼近香农极限。虽然采用MAP算法的Turbo 码的性能指标已经接近了最优[5],但采用MAP算法具体实现的集成电路还存在着两个主要问题:时延和存储需求。在每一次迭代中,来自另一个分量译码器的外信息以累积的形式呈现在当前译码器状态信息和外信息更新中。为了降低译码器状态信息和外信息保存的存储开销,MAP译码器的状态信息和外信息都采用有限字长来表示;为了避免在累加过程中有限字长出现溢出的情况,MAP译码器可以采用归一化来进行处理。归一化方法就是通过寻找更新后的状态信息的最大值,并将该最大值作为基准进行归一化处理。因此,这种算法会带来一定的处理时延和计算复杂度。
本文提出了一种免归一化的MAP算法,避免了传统算法中最大值搜索和处理的相关过程及计算[6]。利用二进制补码的基本原理,将有限字长的二进制补码表示的数值映射到一个归一化圆上,这样以二进制补码表征的状态信息和外信息也映射到该归一化圆上。利用二进制补码运算的基本原理,MAP算法中的状态信息和外信息的更新计算过程转换为相关数值点在圆周上的运动。如果能够通过这些数值在该圆周上的相对位置关系,获得这些数值的相对大小关系,根据MAP算法的基本原理,就可以获得正确的概率信息,且没有性能的损失。这就是免归一化MAP算法的基本思想。本文还给出归一化圆半径的确定方法。性能仿真和电路实现验证了本文所提出的算法不会损失译码性能;与传统方法相比关键路径时延降低了17.4%,复杂度降低了36.2%。因此,本文提出的算法能有效地改善MAP译码器的时延和复杂度。
1 MAP算法原理及其归一化处理
为了便于陈述,表1列举出了本文使用的一些主要符号和其定义。

表1 本文所用符号汇总
Turbo编码器将信息符号及根据码约束关系获得的校验符号一起发送出去。接收器接收到发送过来的带有噪声的数据后,MAP译码器从头至尾扫描接收到的数据来识别前向可能的译码路径关系,然后又从尾到头获得后向可能的译码路径关系;最后根据大量前向和后向的搜索结果,从所有可能的路径中寻找出最佳的译码路径。最优路径是对所有输入数据的最佳推测。例如,一个长度为 15 的数据帧被送入MAP译码器,Turbo码的状态空间S为8,译码路径如图1所示。

图1 译码路径
译码过程中,αk=(αk(0),αk(1),…,αk(s-1))从前向由αk-1获得,βk=(βk(0),βk(1),…,βk(s-1))从后向由βk+1获得。根据MAP算法,状态信息表示从一个步骤到下一个步骤的状态转移概率,表示状态信息的字长或者位宽在实现过程中会受到一定的限制。如果在状态信息变化过程中发生溢出,就会产生误码,而且误码会扩大,导致MAP译码器无法正常工作。因此,状态信息必须归一化[7]。
αk和βk-1的计算方法如下:
(1)
(2)
当s∈S-1、s′∈S时,γk(s′,s)这样定义:
γk(s′,s)=p(sk=s/sk-1=s′)=
(3)
这样,外信息的计算方法是
(4)
为了简化计算,在大多数实现中采用了log_MAP算法[8-9],将乘法和除法转换为加法和减法。简化计算如下:
(5)
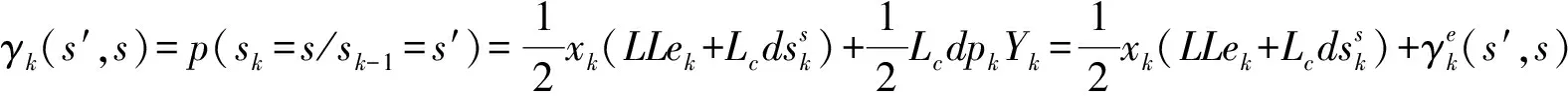
ln(ea+eb)=LOG_SUM(a,b)=
max(a,b)+ln(1+exp(-|b-a|))。
(6)
在实现过程中,ln(1+exp(-|b-a|))可以通过查表法来实现。根据之前的研究,大小为8的表就可以提供足够的精度。
Log_MAP中的归一化可以修改为
(7)
(8)
在Log_MAP中,外信息是
(9)

因此在执行归一化算法时每一步都要做S-1次比较和S次减法。如果在归一化期间不需要估计状态信息的最大值,那么在译码器实现过程中就会降低解码延迟并减小计算复杂度,达到提高计算速度的目的。
本文提出的免归一化算法,目的就是省略在归一化中寻找最大状态信息的过程。因为在MAP译码算法中,重要的不是获得各状态信息的绝对值,而是正确计算和表征各状态信息之间大小的相对关系,即在迭代过程中,具有相对大的状态信息比相对小的状态信息对于算法的正确收敛贡献更大。
2 免归一化MAP算法
根据Log_MAP算法的思想[6],每一步更新后的状态信息是一组介于0和负无穷(实际上是0到负数的界限)之间的数字。如果一种状态信息越趋近于0,那就表明该状态越有可能在最优译码路径上的状态是正确的。假如αk(s)是最大值,αk(s)=0,那么s就是在前向搜索的第k步中概率最高的正确状态。假如βk(s)是最大值,βk(s)=0,那么s就是在后向搜索的第k步中概率最高的正确状态。
在公式(9)中,{αk-1(s′)}的最大值和{βk(s)}的最大值对LLek起主要作用。如果在编码器的输出端dsk=+1 并且解码器的推测是正确的,则LLek为正;如果在编码器的输出端dsk=-1并且解码器的推测是正确的,则LLek为负。如果LLek的绝对值越大,那么在第k步的推测可信度就会越高。如果状态信息的最大值远大于状态信息的次最大值,则LLek将更快地收敛于正确的推测。因此,在译码过程中知道哪个状态具有最大的状态信息对我们来说很重要,但最大值是否必须为0并不重要。


图2 归一化圆

如果状态信息更新期间发生溢出,则投影点将从上半圆逆时针移动到下半圆;如果发生下溢出,投影点将逆时针从下半圆移动到上半圆;如果归一化圆的半径,即表示状态信息的位宽足够大,每个计算步骤的所有状态信息都可以保持在同一个半圆中。也就是说,从最小状态信息到最大状态信息的弧上逆时针运动扫过的角度小于π。
我们可以将αk看作比赛中的跑步者,用比较通俗的描述来解释该原理。如果所有跑步者间的距离始终在半圈内(竞争非常激烈的比赛),则很容易确定谁是领先者。因此,如果αk之间的差值总是小于归一化圆的一半,可以不用去管圆上的绝对位置就能很容易地找到αk的最大值。
在免归一化算法中,可以通过二进制补码加法器和减法器来实现模运算。假设免归一化中使用的二进制补码数据范围为(-C,C),根据Log_MAP算法中的公式(7)和(8),如果满足以下关系,则说明已经进行了归一化:
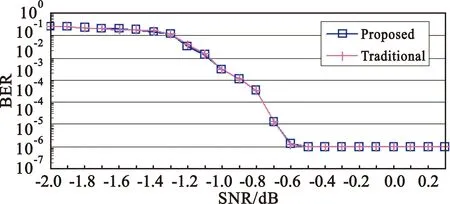
maxAk(s)-minAk(s) (10) maxBk(s)-minBk(s) (11) 免归一化算法的Log_MAP中的归一化修改为 (12) (13) 图3 免归一化处理的实现框图 如果用免归一化方法得到{αk-1(s′)}和{βk(s)},则{αk-1(s′)}的最大值和{βk(s)}的最大值的作用将会得到体现。与公式(9)结果相同,如果使用二进制补码进行计算,当 则会满足以下关系: (14) (15) (16) 因此,我们不需要寻找状态信息的最大值,Log_MAP的计算过程在每一步都得到了简化,也加快了信息更新。由于译码器的样点位宽和信道信噪比是预先定义的,就确定了最大状态信息和最小状态信息之间的差异。因此,即使本文的算法发生溢出时,在Log_MAP计算期间也可以保持状态信息之间的正确关系。可见,免归一化算法对于不同状态信息的更新和外信息的更新效果与传统的Log_MAP 译码算法相同。因此,本文算法在保证不损失译码性能的情况下,能加快状态信息的更新速度并降低计算的复杂度。 本文的免归一化算法的不足之处是在执行模块归一化时需要增加额外的比特位。免归一化MAP算法的位宽可以通过Log_MAP算法中的|maxP+-maxP-| 采用仿真实验来分析免归一化算法的性能。仿真中采用了符合LTE(Long Term Evolution)标准的Turbo码,仿真参数如表2所列。 表2 仿真参数 仿真实验中我们将传统的Log_MAP算法与免归一化算法进行了比较,结果如图4所示。图4(a)显示了Turbo译码器在AWGN通道上译码器的数据帧长度为1 146时的性能,图4(b)显示了Turbo译码器在AWGN通道上译码器的数据帧长度为3 066时的性能。Turbo码的译码有一个明显的特点,就是“瀑布”效益,即在信噪比(Signal-to-Noise Ratio,SNR)增量很小的范围内,如图4(b)中SNR在-1.3~-0.6 dB范围内,误码率(Bit Error Rate,BER)从10-1迅速降低到10-6。Turbo译码的另一个特点是有误码平层,当达到一定的误码率后,如图4(b)中SNR高于-0.6 dB后,BER性能基本保持稳定而不会提升。 (a)数据帧长度为1 146 (b)数据帧长度为3 066图4 不同数据帧长度下Turbo译码器在AWGN通道上的性能 从图4中可以看到,采用免归一化技术的Log_MAP算法的译码性能与传统算法的译码性能基本相同。 对于免归一化算法和传统算法,采用Synopsys公司的EDA工具来实现Log_MAP译码器,在综合仿真中进行了速度优化,表3列出了仿真结果。从表3中的数据发现,与传统方法相比,采用免归一化的Log_MAP算法可以降低36.2%的计算复杂度和17.4%的关键路径延迟。因此,译码器可以以比传统方法更低的复杂度和更高的速度运行。 表3 不同算法的仿真性能对比 本文提出的一种新技术——免归一化MAP算法,通过简化状态信息归一化过程来加速MAP译码器的状态信息更新,可以使Turbo译码器变得更快、更小。这种归一化算法可用于实现ASIC或FPGA技术中的Log_MAP和Max-Log-MAP译码器。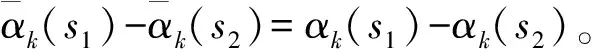

3 性能分析



4 结 论
