基于响应面法的大跨度悬索桥可靠度分析研究

陈绍军，张强，杨钧杰

（1.四川省公路规划勘察设计研究院有限公司,成都610041；2.北京建筑大学土木与交通工程学院,北京100044）

1 引言

近年来，大跨悬索桥不断兴建，其跨径也不断增加。目前，世界上跨度超过1 000 m的已建成的桥梁均为悬索桥，例如，土耳其的博斯普鲁斯一桥和二桥（主跨分别为1 074 m和1 090 m）、中国香港的青马大桥（主跨为1 377 m）、中国的润扬长江大桥南汊悬索桥（主跨为1 490 m）等。大跨悬索桥的分析与设计的理论研究也在不断地深入，这些研究大部分都只是采用传统的方法并基于结构的确定性参数进行确定性的静力分析。但是，显而易见，对于悬索桥这样一种大型、复杂的结构，包含了纷繁的不确定性，比如荷载、材料、几何尺寸的不确定性，这些不确定性必然会对悬索桥的可靠性产生很大的影响，同时，由于悬索桥是一种具有强几何非线性的结构形式，这也会大大增加可靠度分析的计算量。因此，需要发展一种准确而有效的悬索桥可靠度计算方法，这既是大跨悬索桥结构可靠度设计中需要解决的关键问题，也是大跨悬索桥结构健康监测与安全评估系统研究的基础理论问题[1，2]。

本文以某大跨度悬索桥的扁平钢箱梁结构为分析对象，研究扁平钢箱梁结构的可靠度分析方法。为了解决传统响应面方法在分析大型复杂结构可靠度时可能遇到的不收敛或误差较大的问题，通过对迭代步长取值的改进，提出了基于改进响应面的结构可靠度分析方法。在此基础上分别采用改进响应面法和基于响应面的蒙特卡罗法分析了钢箱梁的静力可靠度。最后，讨论了2种计算方法的有效性以及悬索桥结构的几何非线性对可靠度指标的影响。

2 改进响应面法

本文采用响应面法分析大跨悬索桥扁平钢箱梁结构的静力可靠度问题。取不含交叉项的二次多项式作为响应面函数，即：

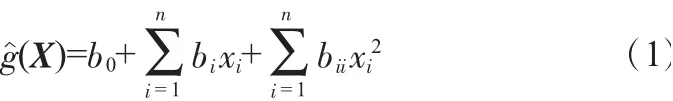
式中，X为相互独立的基本随机变量向量；b0、bi和bii为待定系数；xi为随机变量。

可靠度分析时，响应面法采用了向验算点逼近的迭代策略，即首先从变量均值点附近拟合响应面函数，经过多次迭代使得响应面函数逐渐逼近和吻合验算点附近的真实功能函数。

传统响应面法迭代的具体步骤为[3-6]：

1）假定初始点X(1)=(x1(1)，x2(1)，...，xn(1))，一般取均值点。

2）近似功能函数g(x1(1)，x2(1)，...，xn(1))以及g(x1(1)，x2(1)，...，xi(1)±fσi，...，xn(1))得到2n+1个点估计值。其中，σi为随机变量xi的标准差；f为迭代步长。通常第一步迭代时f可取2～3，此后的迭代过程中f可取为1。

3）利用2n+1个点估计值求解式（1）中的待定系数，从而得到当前迭代点处功能函数的近似极限状态方程。

4）求解近似极限状态方程的验算点X(k)以及可靠指标β(k)。其中，上标k表示第k步迭代。

传统响应面法存在收敛失败和计算误差大的缺点，起主要原因在于迭代步长f的取值。当迭代步长f较大时，由于多项式对实际功能函数的拟合度较差，导致响应面法无法收敛到真实验算点，而是在其附近陷入局部收敛解；当迭代步长f很小时，可以使响应面函数与实际功能函数在真实验算点吻合良好，计算精度较高。然而，对于非线性程度较大的极限状态方程，迭代步长f如果从迭代过程一开始就很小，将造成迭代过程发生不收敛的现象。因此，响应面函数的拟合空间应由大到小逐渐收缩到验算点附近较小的范围内。根据上述分析，本文对传统响应面法的迭代格式加以改进，即采用渐近迭代步长序列f的方法，称为改进的响应面法。也就是在传统响应面法的迭代步骤中，第一步迭代时f取为2，此后的迭代过程中f随迭代步数逐渐减小直至取为0.01。渐近迭代步长序列f的定义如下：

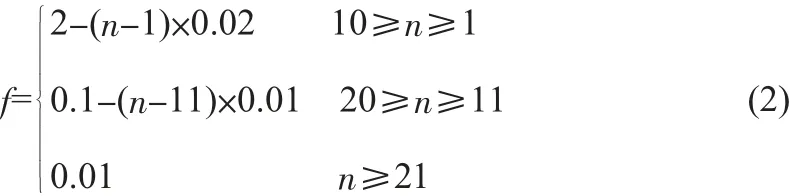
式中，n为迭代步数。

3 实桥可靠度分析

3.1 悬索桥有限元分析模型

该桥是由悬索桥和斜拉桥组合而成的特大型缆索支承型桥梁。其中，南汊悬索桥为主跨1 490 m的单跨双铰简支钢箱梁桥，为中国第一，世界第三。悬索桥桥塔高约210 m，桥主梁采用全焊扁平流线形封闭钢箱梁断面，主缆由平行钢丝索股组成，吊索采用预制平行钢丝束股（PWS），外包PE材料进行防护。

悬索桥结构分析常用脊骨梁模型，通常是将复杂的主梁简化为一根梁单元。但是，脊骨梁模型只考虑了截面的几何性质，没有考虑横向连接系对主梁刚度的影响，即脊骨梁模型不能考虑横隔板对主梁刚度的作用，对于拥有密集横隔板的扁平钢箱梁，模拟将严重失真。同时，悬索桥是一种具有强几何非线性的桥梁结构形式。这种几何非线性来自4个方面：（1）重力刚度，即恒载在主缆中产生的内力会抵抗后续荷载所产生的变形；（2）结构的大位移，即整个结构体系的平衡状态应建立在变形后的状态上；（3）主缆自重垂度，即主缆受力后的变形由弹性变形和自重引起的垂度变化组成；（4）主梁和桥塔的P-Δ效应（重力二阶效应）。在悬索桥结构的可靠性分析中这些非线性必须得到考虑。

根据上述分析，本文对该悬索桥的主缆和吊索采用多直杆法进行模拟，桥塔的模拟则采用三维梁单元。对于扁平钢箱梁，采取简化扁平钢箱梁纵向U形加劲肋的方法，将桥面板及其加劲肋采用网格划分尺寸较大的正交异性壳单元进行模拟，图1给出了该悬索桥的有限元分析模型。对于主梁中的横隔板，也采用板壳单元模拟，这样形成了横隔板、底板和腹板等组成空间箱形结构分析模型，采用空间箱形结构分析模型能准确地模拟扁平钢箱梁的截面特性和质量分布特性，同时可以真实地反映横隔板、横截面畸变和剪力滞后等对全桥响应分析的影响[7]。

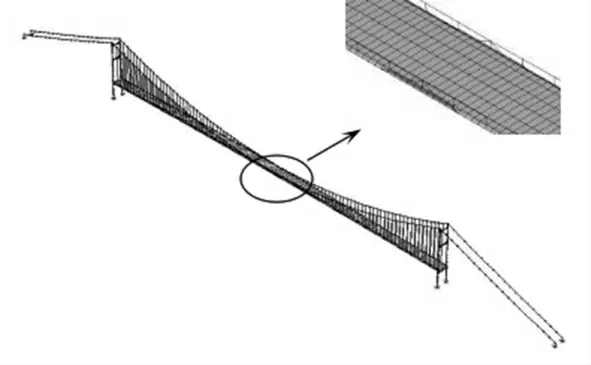
图1 悬索桥有限元分析模型

3.2 可靠度分析

本文考虑的随机变量有悬索桥结构的缆、索、主梁和塔的弹性模量Ei、材料重度γi，缆、索的截面面积Ai，简化的正交异性板的厚度Ti及活荷载q，随机变量总数目为20。变量定义如表1所示。

表1 悬索桥随机变量定义

基于前述悬索桥有限元分析模型及定义的随机变量，进行了悬索桥结构静力可靠度分析。根据JTG/T D65-05—2015《公路悬索桥设计规范》，在正常使用极限状态，悬索桥加劲梁由汽车荷载（不计冲击力）引起的最大竖向挠度值不宜大于跨径的1/250～1/300。本文取为1/300，[δ]=L/300=4 967 mm（L为主跨跨度）。以此建立极限状态方程：

式中，dmid为主跨跨中竖向位移；[δ]为容许竖向位移。

表2 分别给出了采用改进响应面法和基于响应面的蒙特卡罗法（RSM-MCIS法）[8]计算得到的钢箱梁跨中位移的可靠度指标。基于响应面的蒙特卡罗法的基本原理是：采用响应面法构造近似极限状态方程，在已获得近似的显式结构极限状态方程上，采用蒙特卡罗法得到可靠度指标。计算过程表明，由于改进响应面法改进了迭代步长的取值，从而提高了收敛精度。同时，若设定可靠度指标的迭代精度为0.001，则一般迭代2～3次即可收敛，计算时间能够满足实际工程的要求。从表2可以看出，采用改进响应面法可以较准确地计算悬索桥在活荷载作用下的静力可靠指标，而基于响应面的蒙特卡罗法则计算误差较大。另外，悬索桥的几何非线性对扁平钢箱梁的静力可靠度会产生较大的影响。注：RSM-MCIS法结果为抽样10万次分析得到。

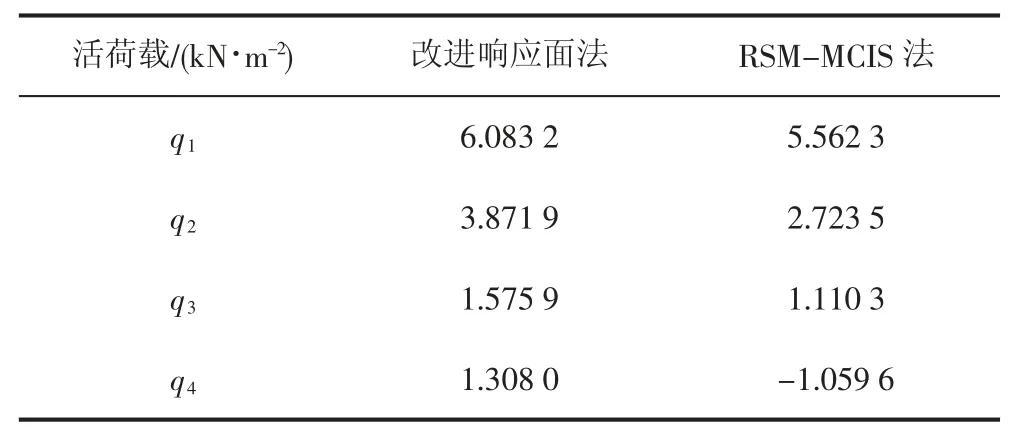
表2 钢箱梁跨中竖向位移可靠度指标

下面讨论2种可靠度分析方法在原理上的区别。响应面法的基本思想是通过一系列有限元数值计算来拟合一个响应面以代替未知的、真实的极限状态曲面。当极限状态曲面比较复杂的时候，这样一个简单的二次多项表达式是不能很好地描述一个复杂的多维曲面的，每一次迭代所得到的二次表达式仅仅只能反映迭代点附近的功能函数的情况，因此，要得到足够精确的验算点的坐标，必然是一个迭代的过程。响应面方法的实质是通过一系列的迭代得到具有一定精度的可靠指标，并不是为了得到结构的极限状态方程的实际表达式，实际上也是不可能的。本文所提出的改进响应面法并没有改变响应面法的基本思路，但通过对迭代步长f的改进，使得响应面法不收敛和精度差的问题得到了很好的改善，所以，采用改进响应面法可以适用于类似悬索桥这种大型复杂结构隐式极限状态方程的可靠度分析。

基于响应面上的蒙特卡罗法(RSM-MCIS)对采用响应面法拟合出的近似极限状态方程进行抽样，当实际的极限状态方程比较简单时，特别是当实际极限状态方程不含交叉项的二次多项式，RSM-MCIS法是精确且有效的。但是，当近似极限状态方程与真实极限状态方程误差较大时，RSM-MCIS法必然会产生较大误差。如表2所示，RSM-MCIS法的分析结果甚至出现了负可靠指标的情况，没有实际的物理意义。因此，对于复杂的悬索桥结构，采用RSM-MCIS法分析得到的可靠度结果是不合理的。

4 结语

本文以某大跨度悬索桥的扁平钢箱梁结构为分析对象，采用改进的响应面法开展了扁平钢箱梁的可靠度分析方法研究。分析结果表明：（1）采用改进响应面法能有效地解决传统响应面法存在的收敛失败和计算误差大的缺点，适用于大型复杂结构隐式极限状态方程的可靠度分析；（2）采用改进响应面法可以较准确地计算悬索桥在活荷载作用下的静力可靠指标，而基于响应面的蒙特卡罗法则计算误差较大；（3）悬索桥的几何非线性对扁平钢箱梁的静力可靠度会产生较大的影响。