弹性地基上龙门吊轨道基础计算
2021-11-02周淦成
周淦成
(中建三局第二建设工程有限责任公司,武汉430074)
1 工程概况
本工程位于南通市海门区境内,预制厂占地106 666.67 m2,主要生产预制箱梁、板梁及箱涵等中大型结构件。其中,最大预制箱梁构件跨径为40 m,重量为1 519 kN。根据工程地质勘测,拟建预制厂的场地,主要地质分布为粉土夹粉质黏土及粉砂夹粉土,视为弹性地基,土体的地基系数K取20 MPa。龙门吊基础长400 m,采用C30钢筋混凝土,倒T形截面尺寸。
预制箱梁采用单台龙门吊移梁,龙门吊型号为MEG90t+90t/5t-45m,额定起重量为1 800 kN(180 t),跨度45 m,起升高度9.5 m。为偏安全计算,考虑移梁时梁的一端距支腿最小可能距离为1 m,则支腿承受最大反力Fmax如式(1):

式中,G1为最大预制箱梁构件重量,取1 519 kN;L1为箱梁重心距支腿距离,取21 m;G2为龙门吊自重,取872 kN;S为行走轨距,取45 m。
大车每边支腿力由2组车轮传递至轨道,每组车轮作用在轨道的力最大轮压力Pmax如式(2):

根据以上所列基本条件,就可以进行基础的计算。
2 文克尔弹性地基假设
文克尔地基模型是由捷克工程师E·文克尔[1]提出,其假设地基表面任一点的沉降与该点单位面积上所受的压力成正比。这个假设把地基模拟为刚性底座上一系列独立的弹簧,弹簧彼此是独立的,忽略了土体之间的横向联系。
利用文克尔地基梁理论,可将地基上的梁分为短梁、有限长梁和无限长梁。根据相关理论分析,划分依据为:(1)荷载与地基梁两端的距离大于3L,为无限长梁;(2)荷载与地基梁一端的距离小于3L,与另一端距离大于3L,为半无限长梁;(3)荷载与地基梁两端距离均小于3L,为短梁。其中,L为地基梁的特征长度,与地基梁的刚度EI和土体的地基系数K有关。
本例中,Iy为截面惯性矩,取3.800 219×10-2m4;C30混凝土弹性模量E取3×107k N·m-2,则地基梁的特征长度L如式(3):

式中,β为特征系数,取0.257 m-1;K为土体的地基系数,取20 MPa。
对于龙门吊轨道,龙门吊一般距梁端最小距离应大于1 m,当龙门吊在距梁端0.5~11.7 m时,地基梁可视为半无限长梁,当龙门吊在11.7~376.6 m时地基梁可视为无限长梁,见图1。
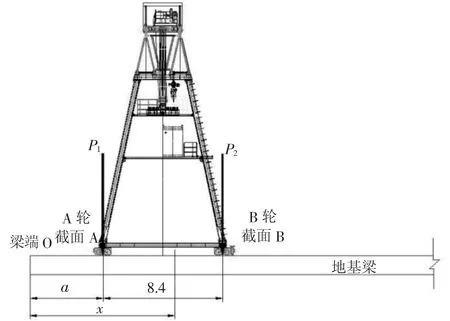
图1 龙门吊轨道受力简图
2.1 半无限长梁
设a为荷载距梁端O的距离,x为计算截面距梁端O距离。当龙门吊一端距梁端O的距离a=1m时,α为荷载至端点O的折算距离,α=βa,ξ为计算截面与端点O的折算距离,ξ=βx。P1与P2为龙门吊轮给轨道的压力,考虑因龙门吊运行过程中产生的动荷载系数γ=1.25,P1=P2=Pmax,则根据文克尔弹性地基梁理论可知以下内容。
在A轮的P1作用下,在截面A处产生的弯矩MA-A如式(4):

式中,φ1~φ4为构造函数;β为特征系数,取0.257 m-1;γ为动荷载系数;Pmax为每组车轮作用在轨道的力最大轮压力,kN。φ1(βx)、φ2(βx)、φ3(βx)、φ4(βx)为引入的构造函数,计算公式分别如式(5)~式(8):

同理,在A轮P1作用下,在截面B处产生的弯矩MB-A=-169.23 kN·m,在B轮P2作用下,在截面A处产生的弯矩MA-B=-10.31 kN·m,在截面B处产生的弯矩MB-B=699.97 kN·m。
因此,在P1、P2轮共同作用下,通过叠加原理可知A截面弯矩如式(9):
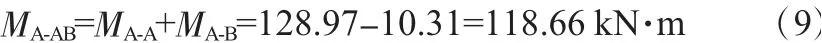
B截面弯矩如式(10):
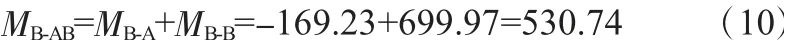
式中,MA-A为在A轮的P1作用下截面A处产生的弯矩,kN·m;MA-B为在B轮P2作用下截面A处产生的弯矩,kN·m;MB-A为在A轮P1作用下截面B处产生的弯矩,kN·m;MB-B为在B轮P2作用下在截面B处产生的弯矩,kN·m。
2.2 无限长梁
当地基梁为无限长梁时,根据文克尔弹性地基梁理论,A轮和B轮在截面A(或B)处产生的弯矩,每个集中力产生弯矩叠加可得式(11):

式中,MB-AB为在P1,P2轮共同作用下截面B弯矩,kN·m;为动荷载系数;Pmax为每组车轮作用在轨道的力最大轮压力,kN;β为特征系数,取0.257 m-1;xA-A为以A轮为坐标原点,截面A处X轴坐标轴,取0;当xA-A取0时,φ3取1;xA-B为以B轮为坐标原点,截面A处X轴坐标轴,取-8.4 m,xA-B取-8.4 m时,φ3取-0.16。
以上分析都只考虑活载的作用,未考虑梁本身自重的影响。实际上,地基梁沿梁长方向,重度是均匀分布的,可知轨道梁自重只会使梁与弹性地基之间产生刚性位移,不会使梁自身产生内力。且梁自重线集度相比龙门吊活载,基本可以忽略。因此,一般不会考虑梁的自重。
3 Mi das/Ci vi l建模
Midas/Civil是广泛使用的桥梁通用有限元分析软件,界面友好,使用方便,广泛用于各类结构的内力分析。通过软件首先定义本文要求的梁截面尺寸和材料,按梁单元建立400 m长地基梁模型,将梁等分成间距1 m单元,利用节点间弹性链接模拟地基的弹性作用.输入龙门吊荷载后,对模型进行计算,最终将计算结果输出分析。由Midas/Civil建模过程可知,软件实际上是把无限超静定结构转换成有限次超静定结构进行分析。
3.1 半无限长梁
利用Midas/Civil建立模型分析后,在龙门吊B轮荷载处存在最大弯矩Mmax=M’B-AB=556.77 kN·m,在龙门吊2个轮之间存在最小弯矩Mmin=-448.11 kN·m。MB-AB与M’B-AB相差26.0 kN·m。由此可知,从弯矩上分析,龙门吊引起的弯矩在整个轨道所影响的范围是比较小的,主要集中在龙门吊大车轮的两侧2倍轮距内。
3.2 无限长梁
在龙门吊B轮荷载处,存在最大弯矩Mmax=M’B-AB=M’A-AB=583.73 kN·m,在龙门吊2个轮之间存在最小弯矩Mmin=-201.28 kN·m。MA-AB与M’A-AB(MB-AB或M’B-AB)相差0.4 kN·m,基本是相等的。同样的,从弯矩上看,龙门吊引起的弯矩在整个轨道所影响的范围是比较小的,最小负弯矩在龙门吊2轮中间处。
4 地基梁的配筋
经过以上分析可知,在梁端附近存在比较大的负弯矩,在地基梁中间部分存在最大的正弯矩。以无限长梁的计算结果进行承载能力极限状态的正截面受弯配筋,取最大正弯矩Mmax=583.73 kN·m及最大负弯矩Mmin=-201.28 kN·m进行配筋计算。
截面尺寸参数为:截面高度h=800 mm,截面宽度为b=550 mm,受拉翼缘宽度bf=1 600 mm,受拉翼缘高度hf=500 mm,受拉区钢筋合力作用点至受拉边缘aS=50 mm。
C30混凝土参数为:抗压强度设计值fc=14.30 N/mm2,抗拉强度标准值ftk=2.01 N/mm2,抗拉强度设计值ft=1.43 N/mm2。
HRB400钢筋参数为:抗拉强度设计值fy=360 N/mm2,弹性模量Es=2.0×105N/mm2。
因此,截面的有效高度h0=h-aS=750 mm,相对界限受压区高度ζb=0.5176。受压区高度x计算式见式(12):
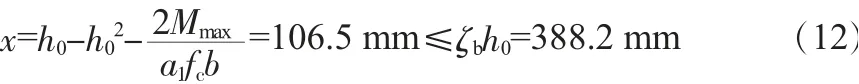
式中,h0为截面的有效高度,mm;Mmax为地基梁最大正弯矩,kN·m;α1为与混凝土抗拉强度标准值有关的系数,取1.00;fc为C30混凝土抗压强度设计值,N/mm2;b为截面宽度,mm;ζb为相对界限受压区高度。
根据α1fcbx=fyAs,As为受拉纵向钢筋的截面积,mm2;可得式(13):

式中,α1为与混凝土抗拉强度标准值有关的系数,取1.00;fc为C30混凝土抗压强度设计值,N/mm2;b为截面宽度,mm;x为受压区高度,mm;fy为HRB400钢筋抗拉强度设计值,N/mm2。配筋率的计算公式如(14):

式中,As为受拉纵向钢筋的截面积,mm2;b为截面宽度,mm;h为截面高度,mm;bf为受拉翼缘宽度,mm;hf为受拉翼缘高度,mm。
根据混凝土结构设计原理要求,可得ρmin如式(15):

式中,ft为C30混凝土抗拉强度设计值,N/mm2;fy为HRB400钢筋抗拉强度设计值,N/mm2。
由所得出的数值可知,配筋率满足要求。
因此,在本工程的实际配置中,需10根公称直径20 mm的HRB400钢筋,实际配置纵向受拉钢筋截面积As=3 142 mm2。同样可以计算在负弯矩下的配筋。
5 结语
运用理论计算法和有限元分析软件计算了弹性地基上的龙门吊轨道梁的内力,并通过弯矩值进行配筋计算。比较后可知,有限元法在无限长梁上的计算结果与理论法是非常一致的,在半无限长梁上的计算误差也非常小,可以直接运用有限元分析软件进行简便的建模计算。龙门吊基础不同于一般的梁,它是由无限个支座支撑的,属于无限超静定结构,无法通过一般的梁理论进行计算。通过上述的弹性地基假设并运用理论和有限元分析软件结合,可以进行很好的模拟计算。
