一种非分段阈值函数的小波去噪算法

梁 伟，陆安江，邹 倩

（贵州大学大数据与信息工程学院，贵阳550025）

1 引言

信号在采集和传输过程中受到采集仪器和传输环境的影响，不可避免会加入一些噪声信号，对目标信号识别和检测的性能造成影响。在信号的分析过程中，首先要滤除目标信号的噪声。信号经传统的傅里叶变换后，有用信号和噪声的频谱在频域中重叠在一起，小波去噪克服了此种不足，使其在信号分析、图像处理和信号去噪等方面得到了广泛的应用。近年来，由于以往的硬阈值函数在阈值处的不连续性及软阈值函数中信号的原始小波系数与估计的小波系数之间存在恒定偏差，影响了去噪效果[1]。为达到更好的去噪效果，目前对于阈值函数的研究也越来越多。然而，在目前的阈值函数的改进方法中，大多文献都是基于参考硬软阈值函数的分段函数进行修改。这些改进的阈值分段函数在一定程度上可以改善去噪效果，但对于原始小波的系数小于阈值系数的舍去和大于阈值系数的保留，没有一定的延缓，如果当阈值选择不好时，可能直接将有用信号滤掉或将噪声信号保留下来。

针对此类问题，提出一种基于反正切函数的非分段阈值函数，该函数在阈值处具有连续性和以硬阈值函数为渐近线，克服了硬软阈值函数的不足，同时具有简化的结构和参数可调节功能。

2 小波阈值去噪原理

一个含噪声信号的数学表示为：

式中，s(t)为目标信号；x(t)为净信号；σε(t)为纯噪声；σ为噪声的强度。

对目标信号s(t)的去噪处理，即是抑制对应的纯噪声信号σε(t)，从而得到净信号x(t)。在信号滤波过程中，在频域对信号进行滤波时，根据净信号与纯噪声信号在频域中所处的频谱分布的位置不同进行分离，从而对噪声进行抑制或滤除[2-3]。然而，当信号频谱和噪声频谱在频域重叠时，在频域中将不能把净信号和纯噪声信号分开，在此种情况下，基于频域的滤波是无效的[4]。而对有用信号进行小波变换后的系数，和对噪声信号进行小波变换后的系数，是根据它们在小波变换域中的幅值来区分的。在通常情况下，经过小波变换处理后，净信号比纯噪声信号的系数幅值小[5]。

经典的阈值处理函数有硬阈值分段函数和软阈值分段函数两种，定义如下：

硬阈值分段函数：

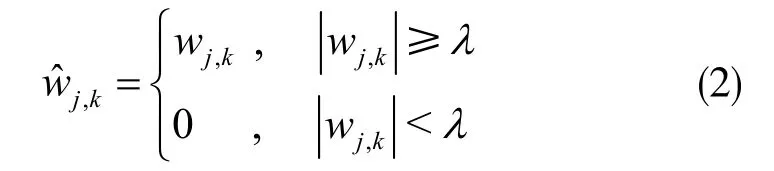
软阈值分段函数：

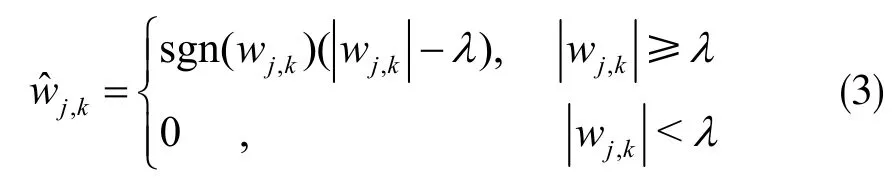
式中，wwjj,k,k为在小波域中的原始小波系数为在小波域中经过处理后的估计小波系数；sgn为符号函数；λ为阈值。硬阈值分段函数和软阈值分段函数的函数图像[6]如图1所示，此处取阈值λ=2。

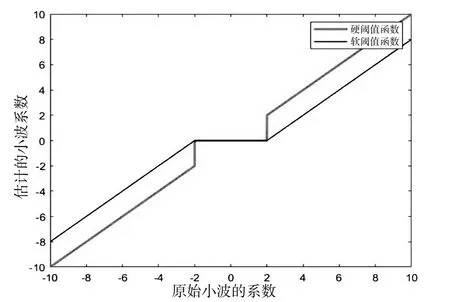
图1 硬阈值及软阈值函数图像

由图中可见，硬阈值分段函数由于在λ处不连续，使重构后的信号存在伪吉布斯效应及振铃现象；软阈值分段函数尽管在λ处是连续的，但是在系数大于阈值绝对值的地方，原始小波系数和估计小波系数存在恒定偏差，对滤波效果存在影响[7]。

3 非分段阈值函数设计

针对硬、软阈值函数的不足，目前，大多数文献都是参考硬、软阈值函数的分段函数形式进行设计，直接将估计小波系数中小于原始值的系数舍去，这对阈值选取的精度提出了要求[8-9]。而此处提出的非分段函数在阈值处是将系数进行缩小一半处理，在阈值左右的系数进行一个逐渐缩放系数的方法进行过渡，从而对阈值选取的精度要求降低了；另外，本非分段函数引入参数，可以通过调节参数来实现在硬、软阈值函数之间的切换，以及调整在阈值附近的系数的缩放程度，并改进硬阈值函数在阈值处的不连续性和软阈值函数的恒定偏差等问题。

反正切函数的数学表达式为：

在数学上，此函数关于原点对称，且具有两条渐近线。在此引入参数m，使函数表达式变为：

其中m可以影响曲线的弯曲程度，m值越大，曲线越弯曲。在此，利用反正切函数图像的特点，结合函数的平移和伸缩变换设计如下非分段阈值函数：

从式(6)中可以分析得到该非分段阈值函数具有的三个特性：

①该阈值函数在定义域是连续的，即函数在阈值处是连续的;

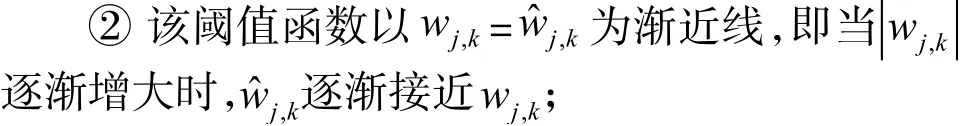
③该函数曲线的弯曲程度受引入参数m影响，m越大，曲线的弯曲程度越大，且该阈值函数图像越来越靠近硬阈值函数图像，当m向0.2由大到小靠近时，该阈值函数图像越来越靠近软阈值函数图像，即该函数可以在很大程度上兼顾硬、软阈值函数的优点，并且可以在它们之间进行调节。

不同参数m下的不同非分段阈值函数图像如图2所示。

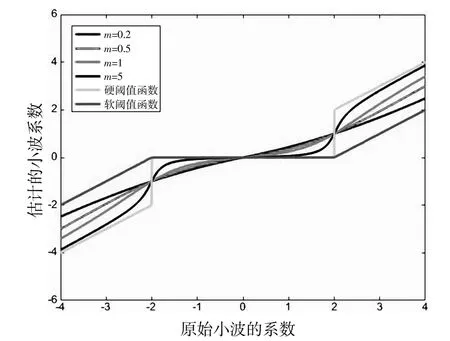
图2 不同m下的分段阈值函数曲线

4 非分段函数的阈值设计

在小波阈值去噪算法中，阈值的选取十分重要，将直接影响信号的去噪质量，实际的阈值应该是恰好大于噪声信号的幅值小波系数时，滤波效果才最好。此处所设计的非分段函数对阈值精准度要求并不那么严格，因其在阈值附近对小波系数处理的方式不同，采取系数压缩的方式进行逐渐过渡，从而可以压缩保留阈值附近的有用信号的小波系数和削减阈值附近的噪声信号的小波系数，达到更好的去噪效果[10-11]。

小波去噪算法的阈值选取方法有很多种，例如无偏估计、启发式阈值、固定式阈值、极大极小阈值、全局阈值等，其中最为经典的是全局阈值，其表达式为：

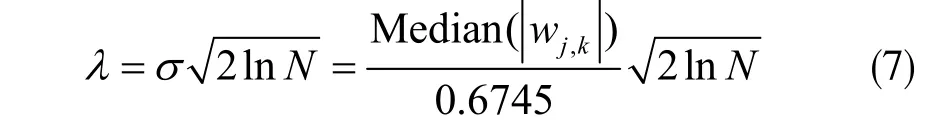
式中，σ为估计的噪声标准方差；Median(|wj,k|)为第一次小波变换后高频系数绝对值的中值；0.6745为噪声标准方差的调整系数；N为信号长度[12]。

5 MATLAB去噪仿真

为验证该非分段阈值函数的有效性，利用MATLAB进行去噪仿真实验。仿真使用的目标信号为blocks高斯白噪声信号和bumps高斯白噪声信号。滤波效果评价指标为性噪比（SNR）和均方根误差（RMSE），SNR越高、RMSE越小，则表明滤波效果越好[13-14]。

分别用硬、软阈值函数、文献[4]、文献[5]和非分段阈值函数进行去噪仿真。仿真使用式(7)中的阈值λ。在文献[4]中的阈值函数为分段函数且对于系数小于阈值的绝对值的函数没有进行压缩，直接让其为零；在文献[5]中的阈值函数为分段函数在阈值附近的系数进行了一定程度的压缩，但是压缩幅度没有式(6)中的阈值函数的压缩度大；文献[4]和文献[5]的阈值函数对阈值处的系数进行完全的保留和完全的压缩处理。仿真测试中的小波基函数均为db8且分层数均为5层。仿真效果如图3和图4所示，详细数据结果由表1给出。

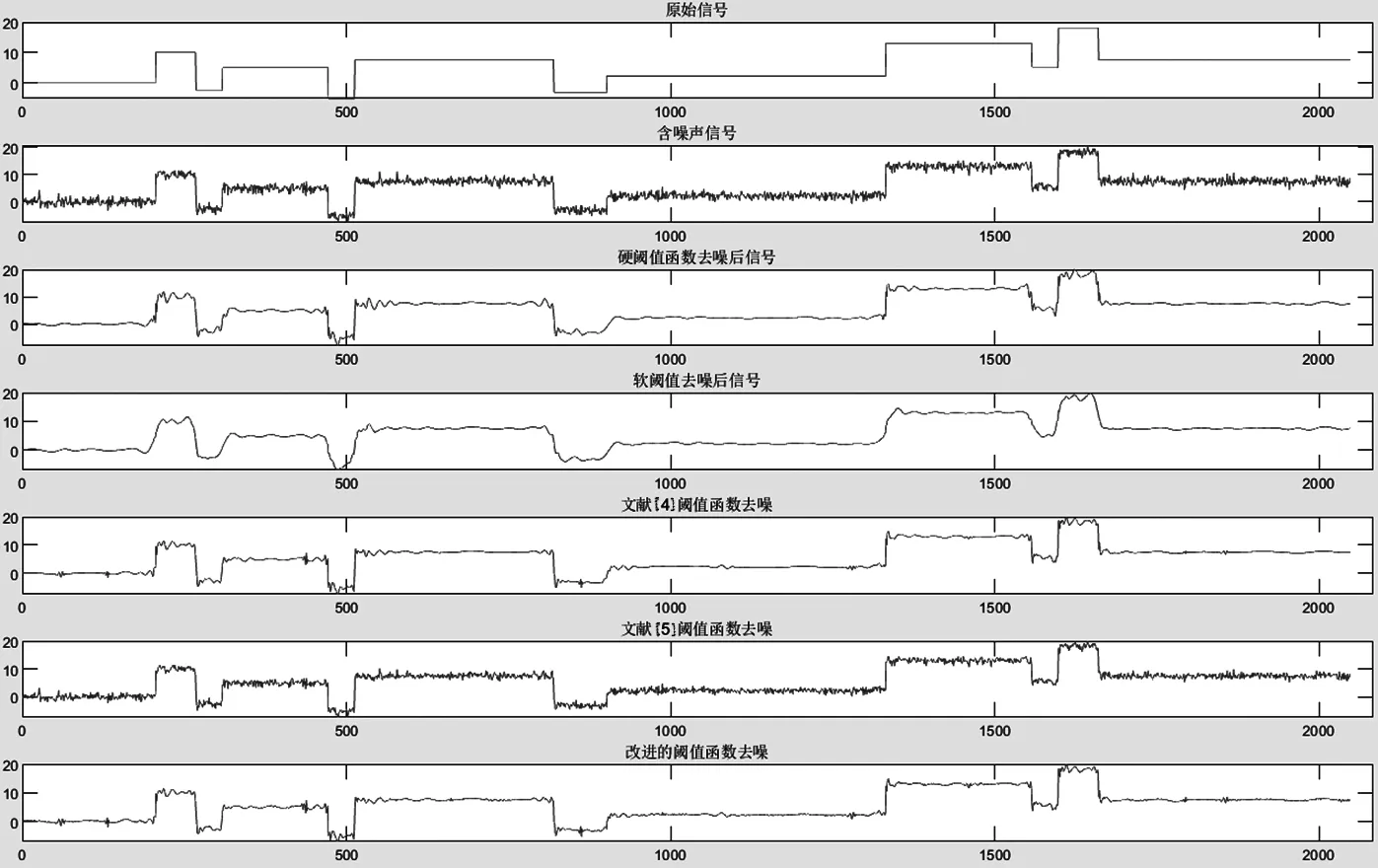
图3 blocks信号去噪效果仿真结果

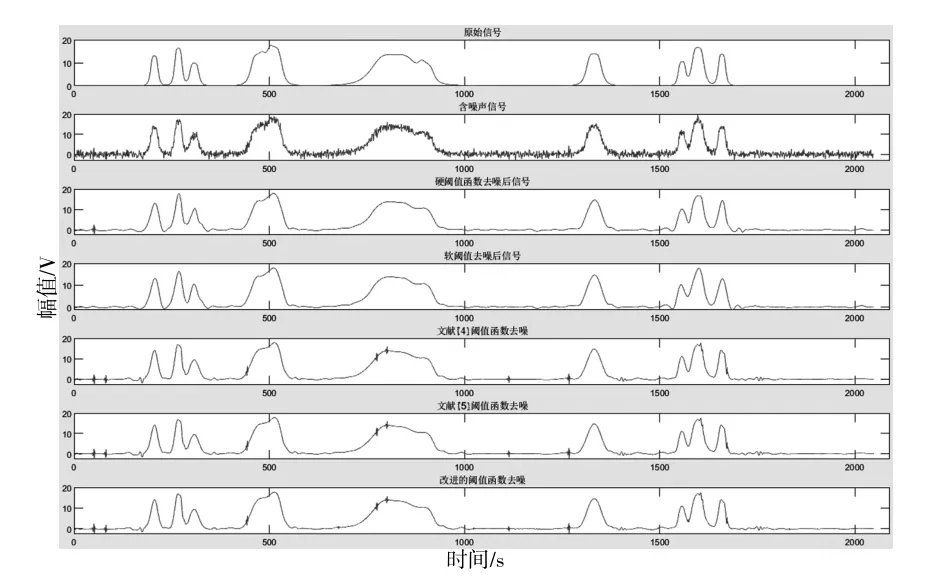
图4 bumps信号去噪效果仿真结果

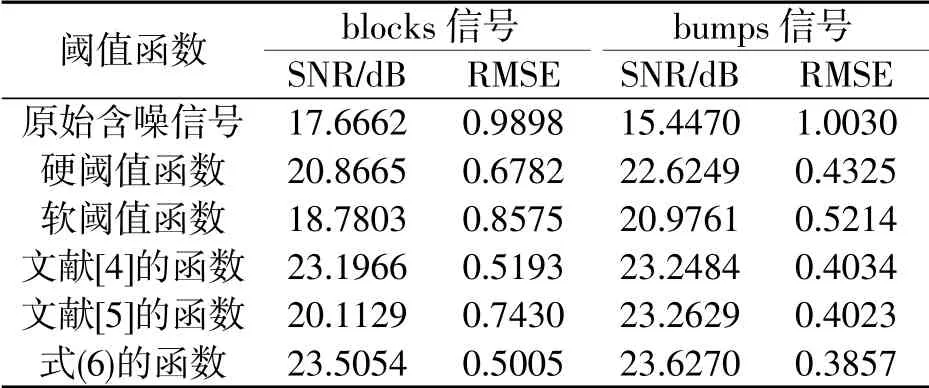
表1 不同阈值函数下的SNR与RMSE

从上述仿真结果可知：

对于两种不同的含噪信号，新函数去噪效果都比传统的硬、软阈值函数的要好，信噪比分别提高了18.57%和8.38%；均方误差分别降低了34.82%和19.13%。

相比文献[4]中的阈值函数，对于不同含噪信号，信噪比分别提高了1.33%和1.63%，均方误差分别降低了3.62%和4.39%。

相比文献[5]中的阈值函数，对于不同含噪信号，信噪比分别提高了16.87%和1.57%，均方误差分别降低了48.45%和4.13%。

相比文献[4]中不同类型的阈值函数，去噪效果相差不是很大，但对于文献[5]中有相同趋势的阈值函数在对blocks含噪信号上有很大的提升。

6 结束语

通过全面分析传统小波去噪的硬、软阈值函数及现有改进的阈值函数的特征及其优缺点，结合反正切函数图像的特点，提出了一种区别于其它阈值函数的非分段阈值函数，并且在非分段阈值函数中引入了参数，以便调节参数大小来达到最好的去噪效果。通过对两种含噪信号使用不同的阈值函数进行去噪，对比仿真数据，所提出的非分段阈值函数的有效性及特有的优点得到了验证。