基于BP神经网络的灌区取水流量在线监测研究
2021-11-02佟强
佟 强
(沈阳市辽中区农业技术推广与行政执法中心,沈阳 110200)
0 引 言
为了解决水资源短缺问题,水资源管理制度得到严格落实,水资源监测能力越来越受到重视。在水资源开发利用中,农业灌溉是占比较大的一部分。做好农业灌溉取水流量的测量计算[1],掌握水量监测数据,对水资源监测具有重要的影响[2]。灌区取水流量在线监测将水量信息提供给管理部门,管理部门根据灌溉用水总量数据,通过管理制度和专业人员分析,达到水资源的合理调配。这个过程中监测方式的合理选择,以及检测技术的准确应用,可以直接影响最终的取水流量数据计算结果。灌区取水流量在线监测方法需要针对不同类型的灌区取水状态,选择不同的流量监测方法[3]。目前,广泛应用的灌区取水流量在线监测方法都存在一些弊端,如成本比较高、后期维护频繁等。在测算过程中,传统方法很容易受到渠道内水草、泥沙等外界因素的干扰[4],影响最终监测数据测量精度。为了使灌区取水流量达到更好的监测效果,实现灌区水资源的统一调度,所以取水流量值的计算是最为重要的环节之一。
本文以BP神经网络为基础,设计灌区取水流量在线监测方法。利用传感器采集灌区水位信息,以传统水流量计算方案为基础,构建基于BP神经网络的计算模型,借助水位信息和计算模型得到灌区取水流量数据。通过水位值和流量软测量模型获取水流量监测数据[5],可以保证监测过程中受到较小的干扰,稳定可靠地实现灌区取水流量在线监测工作[6]。
1 灌区取水流量在线监测方法设计
1.1 采集灌区取水流量信息
文中设计的灌区取水流量在线监测方法[7],是以水位信息采集为基础,结合现场RTU、远程控制端共同完成。水流量监测过程中,采用水位计读取水位信息,并利用现场RTU接收水位值并对数据进行处理。文中设计将两个水位计安装在水流平稳上下游渠道内,并保证二者之间的距离为500 m左右。采用RS485总线实现上游水位计、现场RTU终端的数据传递。针对下游水位计和RTU终端的信息传递,选择433 MHZ短距离通讯。具体的水位计数据传输过程见图1。
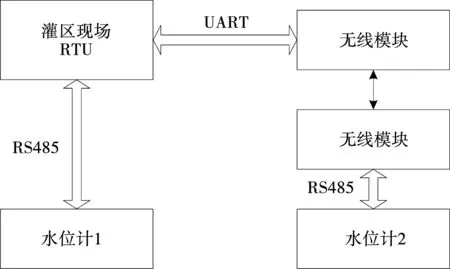
图1 水位计数据传输示意图
由图1可知,在灌区范围内,通常会安装现场终端RTU,承担着数据采集、信息传递的作用。水位计采集的数据通过现场终端RTU进行传递,所以数据的发送方式、数据通信、传输组网的应用都会对最终监测效果产生较大影响。由于灌区内各种外界因素影响,数据的传输不采用有线通信方式。常用的几种无线通信方式及其相关特性对比见表1。

表1 常见通信方式及其特性
通过表1的无线通信方式对比可以发现,GPRS通信方式以数据量为依据进行计费,通过分析发现该方式适用于远程传输工作。文中采用此方式完成RTU与控制端服务器的通信,上下游水位传感器将采集信息传递给灌区现场RTU,然后通过GPRS远程发送到监测平台。最后利用BP神经网络构建的软测量模型[8],基于水位值完成水流量值的计算。
1.2 基于BP神经网络构建计算模型
以BP神经网络为基础构建的计算模型属于软测量建模方法之一,在线性或非线性问题处理中可以发挥极大作用[9]。尤其是人工智能算法的结合,推广了软测量模型在各个领域的应用。该方法与应用过程中,可以将模型中的辅助变量作为输入信息,从而获取输出变量。近年来,基于BP神经网络构建计算模型开始被提出[10],并在应用中提升了数据计算精度。文中针对灌区最常见的自然流梯形渠进行计算模型设计。利用BP神经网络拟合水位-流量关系,通过灌区现场的水位和流量值完成神经网络的训练,将灌区现场采集的数据输入到神经网络中,完成取水流量值的计算[11]。模型构建中应用到最小二乘法,其核心概念是极小值思想。针对比较复杂的函数f(x)和给定的函数p(x),促使其对n个实际数据的误差E=f(xi)-p(xi)对应最小的平方和误差。选择流量计算公式时,若进行最小二乘法的曲线拟合,需要采用水位-流量法对应的水文公式为:
Q=KXM
(1)
式中:Q为断面的流量;X为水位;K和M分别为两个参数。
根据式(1)可以形成拟合曲线图,见图2。
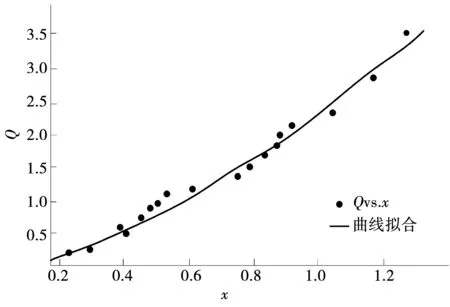
图2 水位-流量函数拟合曲线图
基于BP神经网络构建计算模型后,采用BPNN作为算法核心,结合神经网络模型[12],建立基于拟合曲线的计算模型。针对灌区现场数据,通过仿真对比的方式验证文中设计算法的精确性[13]。BPNN网络拓扑结构见图3,通过3个连接层组合而成,在神经元接受前一级的同时,并将结果向下一级输出。
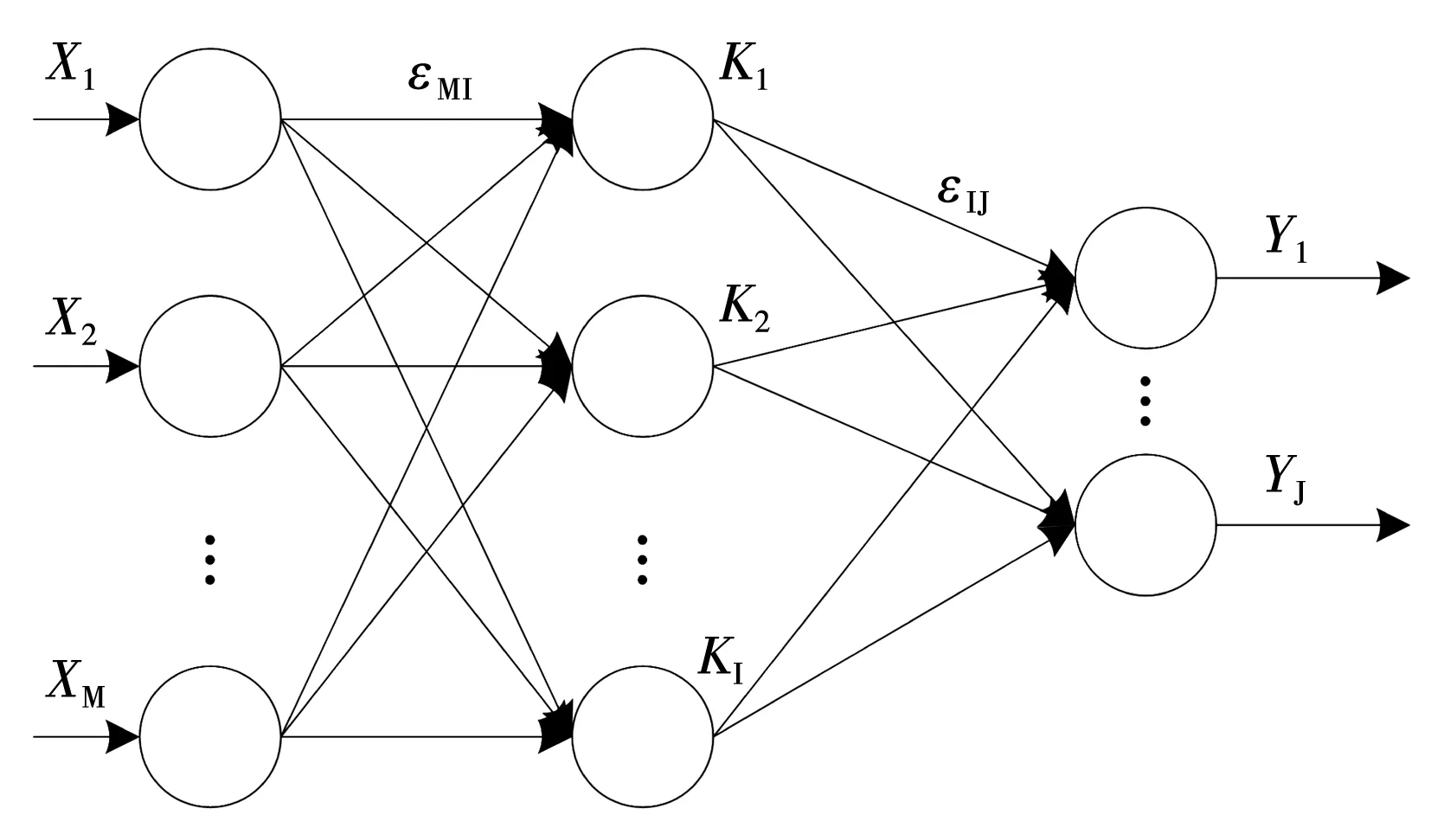
图3 BPNN的网络拓扑结构
图3中XM以输入值存在于神经网络中,输出值用YJ来表示。M和J分别表示输入、输出层神经元的个数。而I表示隐含层神经元数量。用εMI来表示XM到KI的连接权值,εIJ表示KI到YJ的连接权值。应用基于BP神经结构建立的水位-流量测流模型中,包含两个变量信息。变量数据为上游、下游的水位数据,输出的就是渠道流量信息。在模型计算过程中,需要进行n次的迭代计算,该次计算对应的隐含层第i个神经元输入公式为:
(2)
其输出为:
(3)
式中:I为隐含层节点数;V为上一层输出信号;f()为激励函数。
此外,在计算过程中总是存在一些误差的。为了保证计算结果误差降到最小,可以采用最速下降法调整权值,公式为:
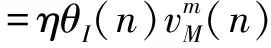
(4)
式中:η和θ分别为学习率、局部梯度。
1.3 确定灌区取水流量计算参数
针对基于BP神经网络构建的计算模型,计算参数的选择直接影响着最终计算结果[14]。在计算模型开始应用之前,依据计算样本的特征信息、模型计算的精确度、模型训练周期,选择并处理建模数据。文中设计的模型以断面的水位值为输入数据,获取输出的取水流量值[15]。将灌区常见的梯形断面明渠作为研究地点,在渠道中选择两个过水断面作为测量点。
计算模型所应用的数据需要从罐区现场来获取,其参数包括水位、流量值等。在断面上选择5~8条测速垂线,将每条垂线中设置3个不同深度的测量点。通过测量点的数据获取垂线的流速,然后依据流速获取对应的水流量信息。在神经网络构建的模型中,应用实际数据进行训练。训练数据选择50组,其余数据当作测试样本。因为在神经网络计算模型中输入的样本大部分不是一个量纲,所以在模型应用之前将需要的数据采用归一化方法处理,确保神经网络计算模型的应用效果。数据归一化处理公式为:
(5)
式中:xi为输入值;ximax为输入参数中的最大值;ximin为最小值;xj为归一化后的无量纲值。
因为输入参数数量有限,采用单隐含层神经网络,并结合sigmod函数进行计算。除此之外,在BP神经网络中,没有一定的标准来确定隐含层的节点数,这一点往往需要通过实际情况来判断。具体的判断结果可以通过以下公式来决定:
(6)
式中:l为隐含层个数;m、n分别为输入层和输出层节点数目;a为常数,其取值范围0~10。
为了实现良好的训练结果,通过MATLAB仿真方式,分析应用不同的隐含层节点数产生数据误差,选择最优节点数目。通过节点个数改变观察数据均方误差、隐含层节点的关系,见图4。
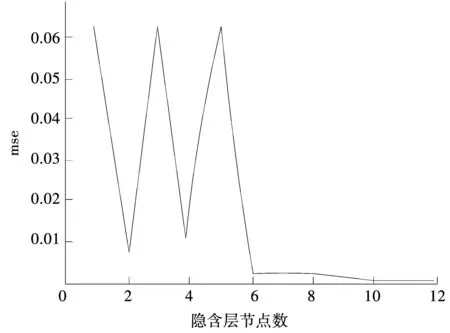
图4 训练节点mse变化图
通过图4可以发现,随着隐含层节点数量的增长,训练数据均方误差处于不断变化的状态。直到节点为6的时候,误差瞬间减少,随后保持比较稳定的状态。因此,将测流模型的隐含层节点数选择为6。
1.4 实现取水流量在线监测
灌区取水流量在线监测中应用的软测量模型需要提前确定完成,在离线时通过实际数据进行仿真建模处理。在检测过程中,将基于BP神经网络构建计算模型保存到远程控制中心,将GPRS传递过来的水位信息输入模型,并在模型的作用下计算灌区取水流量值。具体的数据处理及其模型计算流程见图5。
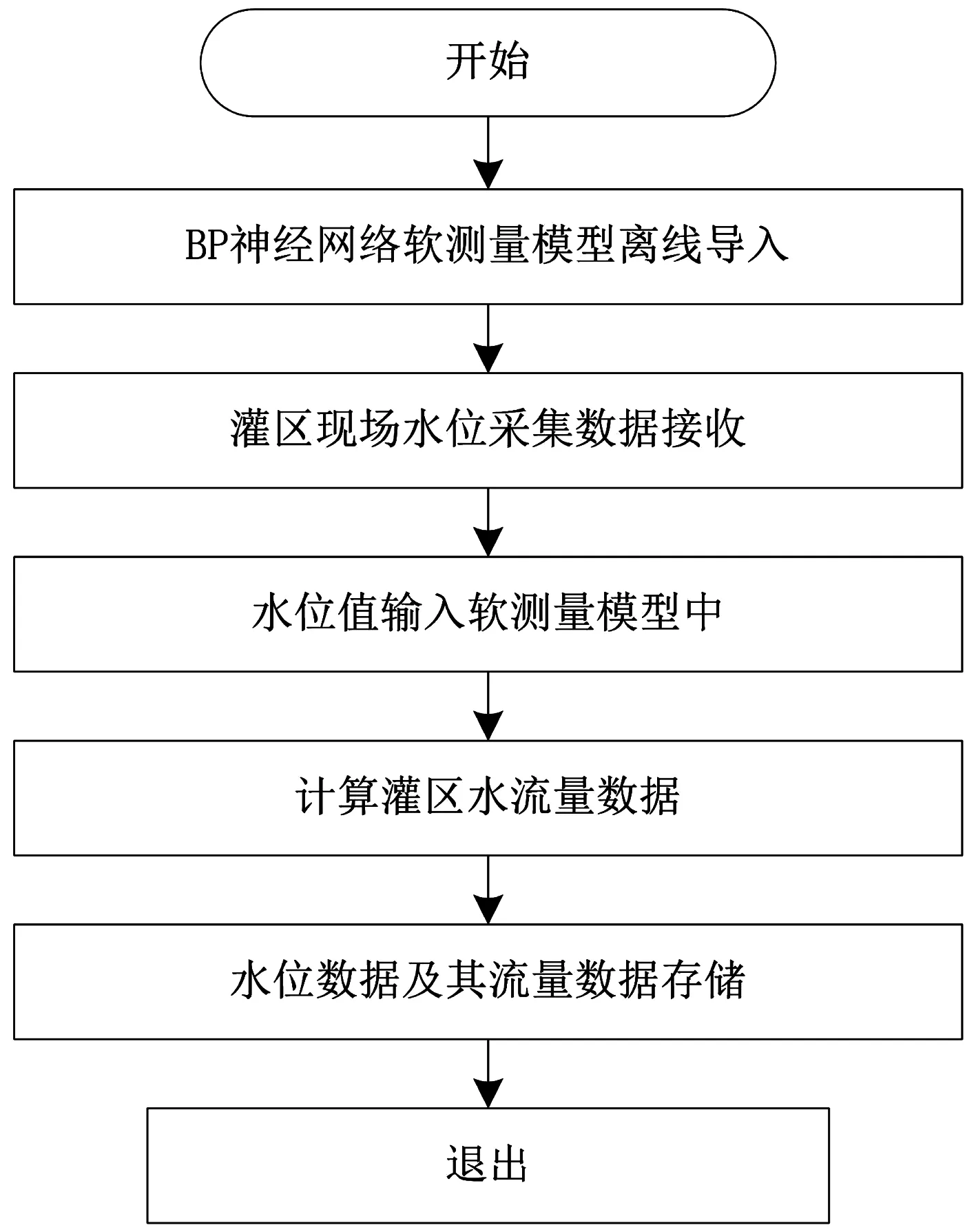
图5 数据处理及模型计算的流程图
将计算后的监测数据通过C/S与B/S结合的上位机架构进行存储。基于B/S模式设计外部服务器,通过客户端浏览器将灌区水位和流量信息的监测数据呈现在工作人员面前。文中采用VS2010的.Net平台,作为监测的显示服务器。
针对灌区监测方法所需要的功能进行设计,在取水流量在线监测实现过程中,需要的基本功能包括读取并显示灌区现场的水位数据、导入测量模型、输入水位数据、计算实时流量值、显示取水流量值变化、保存监测数据等。此外,以报表的形式将数据进行存储,工作人员通过Web登录完成取水流量在线监测,并通过监控点的选择,查询现场水流量监测数据。
除此之外,在取水流量在线监测工作中,监测方案的确定需要以现场实际环境为基础。与现场情况相结合,适当修改监测设备与方法。在取水流量监测时,还需要考虑供电系统稳定性,分析其对监测数据产生的影响,采取相应解决措施,以保证监测数据的误差降到最小。
2 实 验
2.1 实验准备
为了验证文中设计的取水流量在线监测方法具有良好的应用效果,特进行实验。地点选择某一农业灌溉区域,根据调查可知,该区域每年从4月份开始进行取水灌溉,直至8月份结束灌溉工作,属于比较稳定的灌区。将本次测试期限设置为一周,每天对灌区取水流量实际值进行测量,同时应用文中设计的在线监测方法进行在线监测,分析二者数据之间的差异,获得文中设计检测方法的相对误差。为了加强实验结果的说服力,采用两种传统监测方法同时进行监测,对比3种方法的误差,从而判断文中取水流量在线监测方法的可靠性。根据统计,一周期限内灌区取水流量人工测量结果见图6。
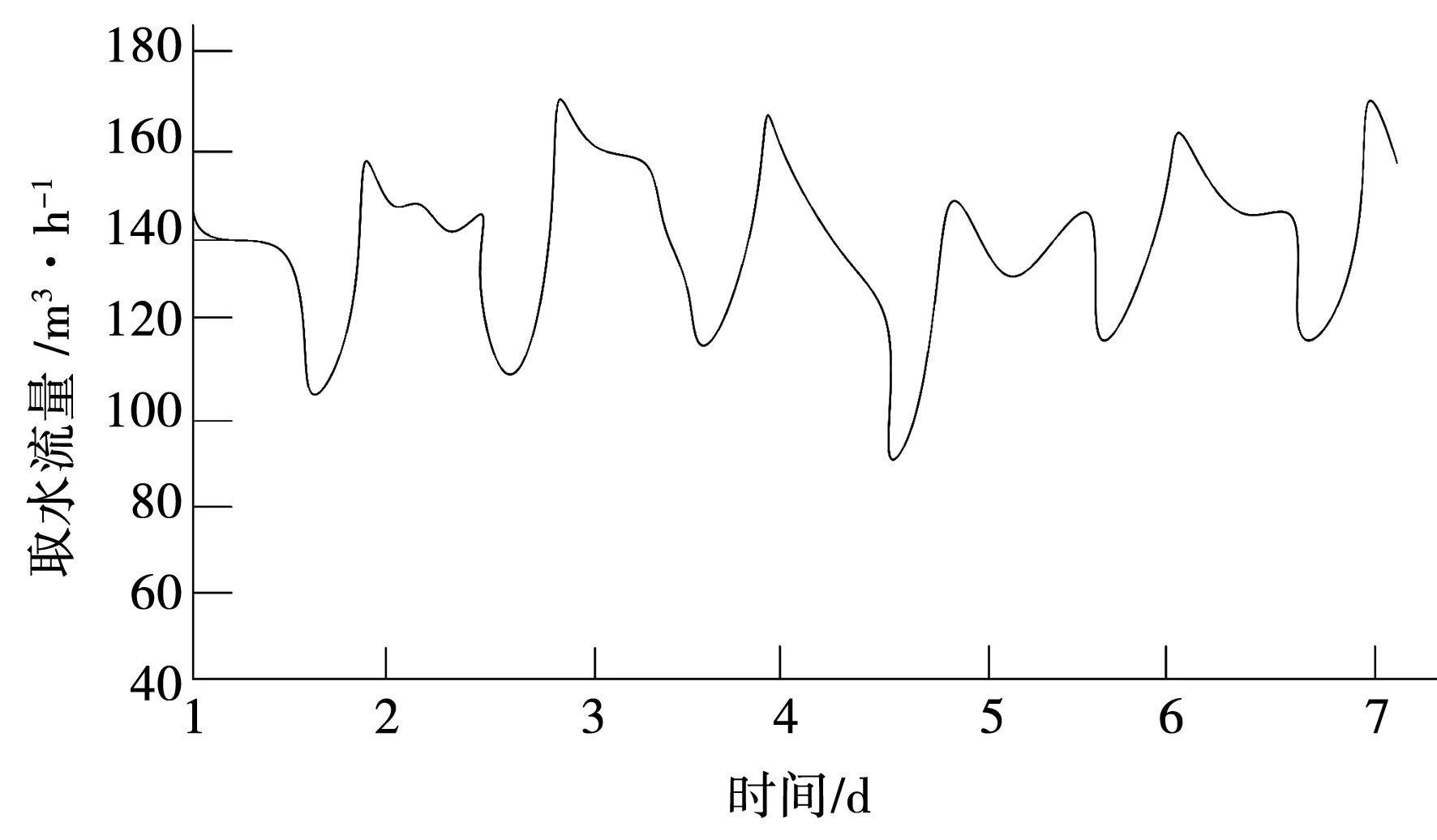
图6 灌区取水流量实测数据统计图
以图6中水量实测数据为基础,进行检测方法相对误差的分析。
2.2 结果与分析
应用3种方法同时进行灌区取水流量在线监测,经过统计后,取水流量监测显示数据见表2。
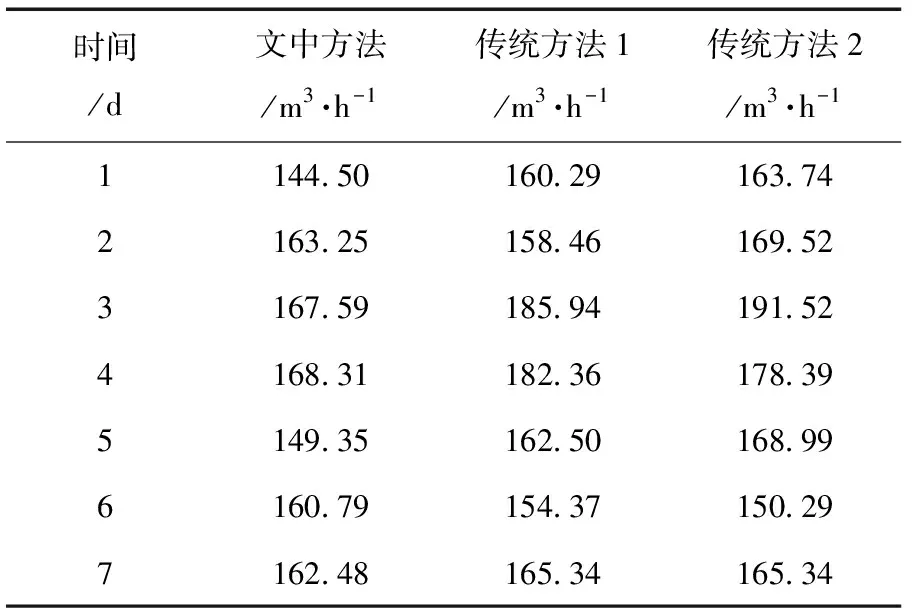
表2 3种方法灌区取水流量监测数据
针对表2中数据进行分析可以发现,运用3种监测方法可以获取灌区每日取水流量数据,但所获取的数据相对实测数据来说包含一定误差。并且随着监测方法的不同,产生的误差大小也不相同。在与实测数据对比分析后可知,文中设计的灌区取水流量在线监测方法所获取的数据是3种方法中误差最小的,最贴近实测数据。而两种传统方法中,传统方法1误差小于传统方法2。将每日取水流量监测数据与实测数据进行对比,绘制相对误差对比图,见图7。
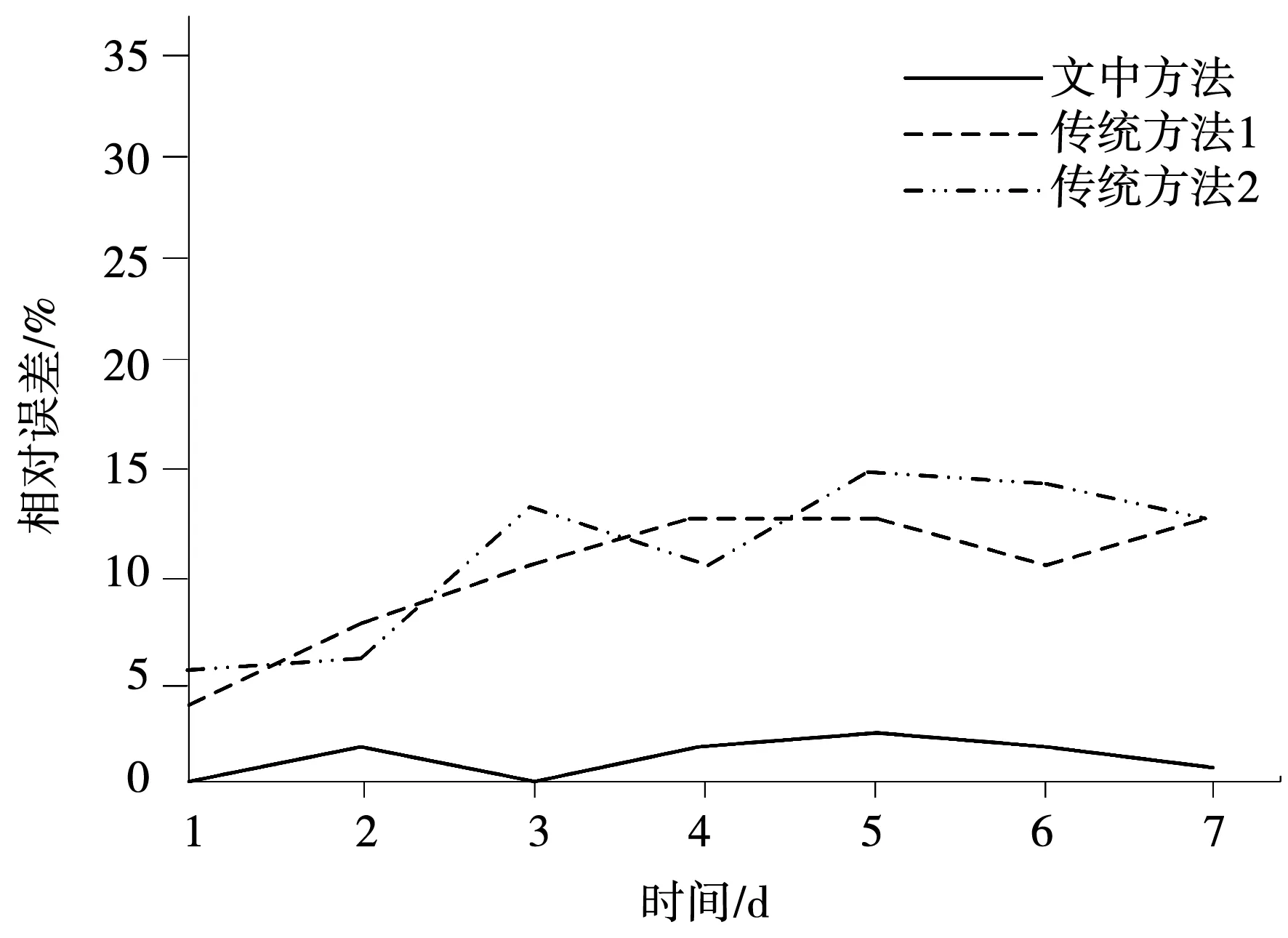
图7 3种监测方法误差对比图
由图7可知,文中设计监测方法其相对误差最高仅为2.31%,并且某些时候可以使得监测数据和实测数据保持一致。而传统方法1和传统方法2的最高相对误差分别为12.59%和15.68%,甚至相对误差最低为4.02%和5.98%。通过计算可知,文中设计监测方法的平均误差为1.52%,相比两种传统方法,将平均误差分别降低8.53%和9.54%。因此,将文中设计的在线监测方法应用于灌区取水流量监测中,可以有效降低监测数据的相对误差,从而提高在线监测的可靠性,发挥更加良好的效果。
3 结 语
本文以BP神经网络为基础,设计了取水流量在线监测方法,通过人工智能技术的应用,促进了灌区水流量监测对水资源管理调度工作的重要意义。本文研究在实际应用中达到良好的预期效果,增强了在线监测的可靠性。但是文中的研究仅仅针对监测数据精度进行研究,未来针对水流量监测方面还可以进行深入研究。从灌区信息化监测平台的设计上来看,还可以进行全方面设计。添加流量软测量模型,以及接收水位采集信息板块,提升信息灌区取水流量在线监测的效率,并加入异常警报等功能,提升取水流量监测方法的性能。
