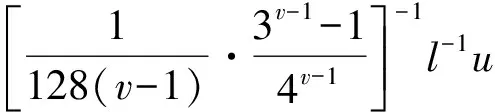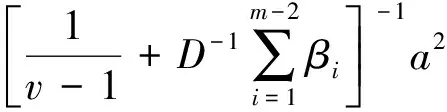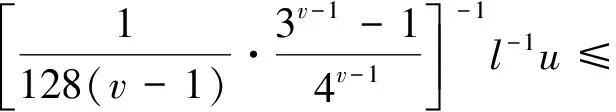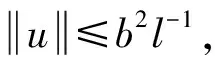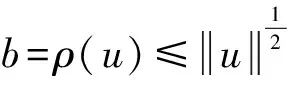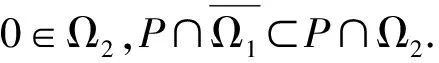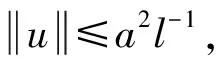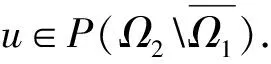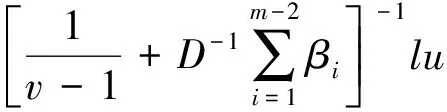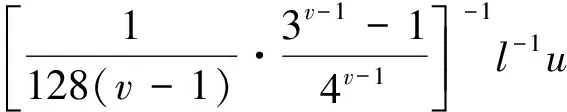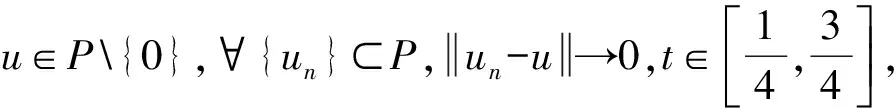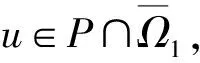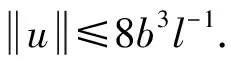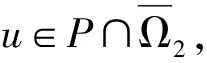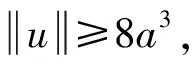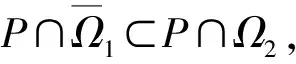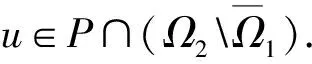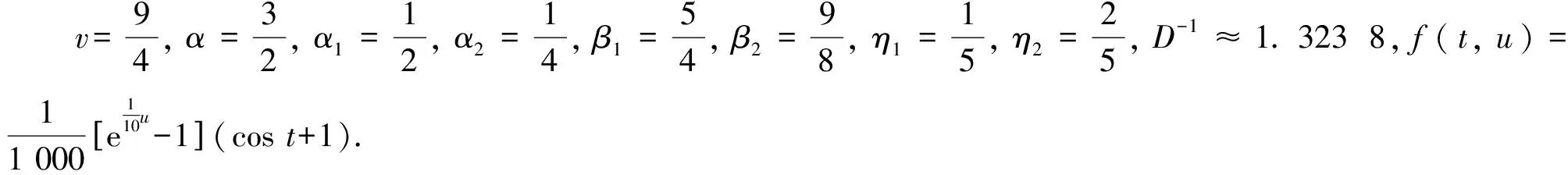一类具有适型分数阶导数的分数阶微分方程m点边值问题的正解
2021-11-02赵微
赵 微
(大庆师范学院 数学科学学院, 黑龙江 大庆 163712)
近几十年来,关于分数阶微分方程边值问题的研究受到了许多学者的关注,详见文献[1-5].Tian[1]运用Leggett-Williams不动点定理,研究了一类Riemann-Liouvill分数阶微分方程边值问题,得到了多个正解存在的结果.王永庆等[2]运用锥拉伸与压缩不动点定理,研究了一类Riemann-Liouvill分数阶微分方程m点边值问题,得到了正解的存在性.Khali等[3]定义了一种新的分数阶导数定义,称为“适型分数阶导数”,Adbel等[4]进一步深入研究了这种适型分数阶导数的相关性质.董晓玉等[5]讨论了上面这种具有“适型分数阶导数”的两点分数阶微分方程边值问题,得到了相关问题正解的存在性.上述文献大多采用锥拉伸与锥压缩不动点定理或者Leggett-Williams解定理,得到了分数阶微分方程边值问题正解存在的结果.费祥历等[6]引入了一种新定义的泛函,其中凹泛函、凸泛函都满足这种泛函的定义.并在此基础上,建立了关于这种泛函形式的锥拉伸与锥压缩不动点定理,推广或改进了己有的许多结果.如薛益民等[7]运用的范数形式的锥拉伸与压缩不动点定理,包含在这种新的泛函形式中.因此该定理的应用范围更广泛一些.
受上述文献的启发,本文研究如下m点适型分数阶导数定义下的分数阶微分方程边值问题:
Dvu(t)+h(t)f(u(t))=0, 0 (1) u(0)=u′(0)=0 (2) (3) 式中:Dv、Dα、Dαi是适型分数阶导数,0<αi<α≤2 为方便起见,首先给出一些必要的定义和引理,推导出相应的分数阶微分方程的格林函数,并给出格林函数的一些性质. 定义1[5]连续函数f∶(0,+∞)→R的α∈(n,n+1]阶适型分数阶导数定义为 由适型分数阶导数的定义,可知α=1时,适型分数阶导数就是传统的一阶导数的定义. 定义2[5]连续函数f∶(0,+∞)→R的α∈(n,n+1]阶分数积分定义为 其中:In+1是n+1重积分算子. 引理1[5]设α∈(n,n+1],u∈C(0,+∞)具有α阶适型分数阶导数,则 IαDαu(t)=u(t)+C0+C1t+…+Cntn 其中:Ci∈R,i=0,1,2,…,n. 引理2给定y∈C[0,1],则关于问题Dvu(t)+y(t)=0,0 其中 证明由引理1,可得上述问题的通解如下: 根据式(2)可知,c0=c1=0.另一方面,参考文献[10]中Dα(tp)=ptp-α,则可从式(3)中得到 经过计算可得 于是有 引理3令G(t,s)为引理2中所给,这里称其为格林函数.则它满足: 证明1) 当0≤s≤t≤1时, 当0≤t≤s≤1时, 由k(ηi,s)≤1,则可得 为方便,做如下假设: (H2)f∶[0,+∞)→[0,+∞)是连续的. 定义算子: 引理4设条件(H1),(H2)满足,则A∶P→P全连续. 证明由引理3及算子A的定义,有 且 则显然知A∶P→P全连续.如果A有不动点u≠0,则u是问题(1~3)的正解. 定义3(Property A)[6]称P上非负连续泛函ρ∶P→[0,+∞)满足PropertyA,如果 ρ(λx)<ρ(x),∀x∈P{0},λ∈[0,1) 显然,ρ(0)<ρ(x),∀x∈P{0}. 注1由上述定义3可知,凹泛函、凸泛函、次线性泛函都满足Property A[6].因此这类定义的泛函范围更广一些. 2)ρ(Tx)≥ρ(x)且Tx≠x,∀x∈P∩∂Ω. 则必有i(T,P∩Ω,P)=0. 定理1假设(H1,H2)满足,如果存在常数a和b,0 ∀b2l≤u≤b2l-1 ∀u≤a2l-1 则问题(1~3)至少存在一个正解. 证明根据定理条件,注意到u≤b2l-1,则有 令 于是ρ∶P→[0,+∞)是非负连续泛函且ρ(u)=0⟺u=0,当u∈P{0}时, λ∈[0,1) 说明ρ满足PropertyA. 取Ω1={u∈C[0,1]|ρ(u) 因此,有 根据引理6可以得到 i(A,P∩Ω1,P)=0 (4) 如果u∈P∩Ω2,则有 假设A在P∩∂Ω2上没有不动点. 如果u∈P∩∂Ω2,根据引理3,有 根据引理5可知: i(A,P∩Ω2,P)=1 (5) 由式(4)和式(5)易得 定理2假设(H1),(H2)满足,如果存在常数a和b,0 ∀u≤8b3l-1 ∀8a3l≤u≤8a3l-1 则问题(1~3)至少存在一个正解. 证明根据定理条件,注意到 8b3l-1<8l2a3l-1=8a3l 令 于是ρ∶P→[0,+∞)是非负泛函且ρ(0)=0. 上述意味着ρ∶P→[0,+∞)是非负连续泛函. 进一步可以得到ρ(u)=0⟺u=0,且 ∀u∈P{0},λ∈[0,1) 说明ρ满足PropertyA. 假设A在P∩∂Ω1上没有不动点,则由引理5得 i(A,P∩Ω1,P)=1 (6) 再根据引理3有 假设A在P∩∂Ω2上没有不动点,则根据引理6有 i(A,P∩Ω2,P)=0 (7) 注2本文应用了两个不同的满足Property A的泛函.通过计算不动点指数,得到了适型分数阶微分方程边值问题(1~3)至少有一个正解存在的结果.值得指出的是,在定理1中所用的泛函既非凸泛函也非凹泛函,这类泛函较以往所用的范围更广.如薛益民等[10]运用的Guo-Krasnosel’skii’s不动点定理,是非负连续泛函,就包含在这种新定义的泛函中,也可以用本文中提到的这类新泛函不动点定理来证明解的存在性. 例1考虑如下的分数阶微分方程:1 准备工作
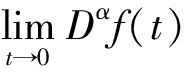

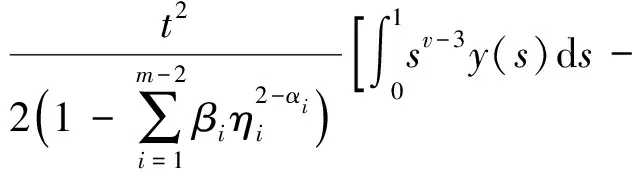
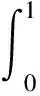
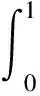
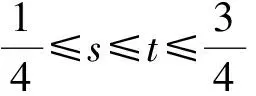
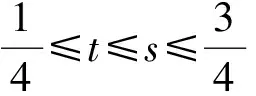




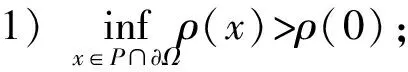
2 主要结论