轻量级的三维点云识别方法

欧阳宁，陆兆能，林乐平

(1.桂林电子科技大学 认知无线电与信息处理省部共建教育部重点实验室，广西 桂林 541004； 2.桂林电子科技大学 信息与通信学院，广西 桂林 541004)

0 引 言

近年来，卷积神经网络(convolutional neural network，CNN)在图像识别[1]、图像去模糊[2]、图像分割[3]等领域取得的突破性进展已经影响到了三维点云识别领域。斯坦福大学的Qi等[4]提出将CNN直接应用于不规则点云的开创性方法，该方法利用CNN强大的特征学习能力来逐点地提取点云高维特征，提高点云识别性能。然而，该方法没有考虑点云的局部结构特征，限制网络识别细粒度特征的能力。因此，许多学者通过设计多层级或多尺度的网络结构来获取丰富的局部结构特征，以提高网络模型的识别准确率。然而，点云信息量有限，多层级或多尺度的网络结构会提取大量的冗余信息，导致网络模型时间和空间复杂度高的问题。

针对以上问题，本文提出一种轻量级的三维点云识别方法(LPCR-Net)。该方法通过在点云空间构建一种高效的K近邻图来获取点云的局部结构信息，以保证网络模型取得高识别准确率的前提下降低计算复杂度。首先，使用最远点采样法[5](farthest point sampling，FPS)从原始点云中获取采样点，以采样点作为K近邻图的节点，能够大幅度减少冗余的局部结构信息，同时降低计算复杂度。其次，使用注意力机制[6]来突出局部区域不同K近邻点的重要性，以增强局部结构特征的表达能力。然后，利用分组卷积[7]提取高层次的局部结构特征的同时减少卷积层的参数量。最后，在保证网络模型取得较高识别准确率的前提下减少全连接层的层数与节点数，以减少全连接层的参数量。实验结果表明，本文方法的识别准确率达到当前主流方法同等或更优水平，并且网络模型的时间和空间复杂度大幅度降低，同时保持较高的鲁棒性。

1 相关研究

在计算机三维视觉中，三维点云识别是一项重要的任务。在基于深度学习的三维点云识别中，由于三维点云具有无序性和稀疏性，通常需要转化为规则的体素[8,9]或多视图[10]后才能够使用CNN进行特征提取。但是这些转化过程都会导致点云几何信息的丢失，同时需要较大的内存开销。因此，直接使用CNN提取原始点云特征的方法成为当前研究的重点。

Qi等[4]提出将CNN直接应用于不规则点云的开创性方法，该方法使用1×1的卷积逐点地提取点云的特征，并使用最大池化层作为对称函数来获取具有排列不变性的全局特征。为了能够降低网络模型的计算复杂度，Bai等[11]在PointNet的基础上设计了一个轻量级实时点云识别网络LightPointNet，在保证识别准确率不低于PointNet的同时，模型参数量大幅度降低。但是，这两种方法都没有考虑点云的局部结构特征，使得网络的识别能力受到限制。为了解决这个问题，Qi等[5]提出多层级局部特征特征提取网络PointNet++，该网络首先对点云进行采样和分组来构造两个不同大小的局部结构，然后使用PointNet逐层提取局部结构特征，从而提高网络识别细粒度特征的能力。Liu等[12]提出多尺度特征融合网络Point2Sequence，该网络首先构建点云空间局部区域的多尺度结构并提取相应的尺度特征，然后利用具有编解码结构的循环卷积网络来学习局部区域多尺度特征之间的相关性，获取更具有鉴别能力的局部结构特征。

受到图卷积神经网络能够有效处理非欧几里德数据的启发，Wang等[13]提出用于点云识别的动态图卷积神经网络DGCNN，该网络在点云逐层的特征空间中构建K近邻图，使用边缘卷积提取每个点的边缘特征，并使用最大池化层来聚合所有边缘特征以获取局部几何结构特征。在DGCNN基础上，Zhang等[14]移除空间变换网络，同时引入密集连接的方法将DGCNN不同层级的特征连接起来，以提高网络的识别准确率和减少模型参数。Cheng等[15]采用多头部的图注意力机制来获取丰富的局部结构信息以及增强网络的稳定性。

当前，基于深度学习的三维点云识别方法已取得突破性进展。许多研究工作表明，点云的局部结构特征获取对于网络的识别准确率的提升尤其重要。为了获取更具有表达能力的局部结构特征，在网络结构设计上采用多层级或多尺度的结构。然而，点云信息量有限，多层级或多尺度的结构会提取到大量的冗余信息，使得网络的识别准确率提升有限，并且会大幅度提高网络的时间和空间复杂度。其次，在使用K近邻图获取点云的局部结构信息的方法中，直接使用原始点云的所有点来构建K近邻图也会大幅度增加网络的计算复杂度。

基于前人的研究基础上，本文提出一种轻量级的三维点云识别方法，在保证良好的识别准确率的前提下降低网络模型的时间和空间复杂度，以满足移动端、嵌入式设备等实际应用需求。

2 轻量级的三维点云识别模型

2.1 网络模型整体结构

本文设计的网络模型由4部分组成，如图1所示。第一部分，使用最远点采样法(FPS)对原始点云进行采样，获得采样点云；第二部分，以第一部分获得的采样点云和原始点云作为图注意力模块的输入，计算点云的局部结构特征；第三部分，由两个卷积层和两个分组卷积模块组成，用来进一步提取高层次的局部结构特征；第四部分，使用最大池化层(MaxPool)作为对称函数提取具有排列不变性的全局特征，并使用全连接层与Softmax层对全局特征进行分类得到点云的类别概率输出。

图1 网络模型整体结构

第一部分，网络模型的输入为原始点云X={xi∈R3,i=1,2,…,N}，输出为采样点云X′={xj∈R3,i=1,2,…,M}，其中N为原始点云数，M为采样点云数，每个点包含三维坐标(x,y,z)。使用FPS对表示椅子的原始点云进行采样，采样点云的可视化如图2所示。其中，图2(a)为具有1024个点的原始点云，图2(b)和图2(c)分别为具有512个点和256个点的采样点云，通过点云可视化图可知，采样点云保留了原始点云较为完整的几何结构信息。

图2 点云可视化

第二部分，本文设计的图注意力模块使用K-NN图表示点云的局部结构，以采样点作为图的节点，采样点与其K近邻点的差作为图的边。使用卷积核大小为1×1的卷积层提取节点和边缘的特征，并根据节点和边缘的特征计算得到注意力系数，使用注意力机制来突出局部区域不同K近邻点的重要性，以增强局部结构特征的表达能力。局部结构特征的获取，有助于提高网络模型的识别准确率和鲁棒性。

第三部分，局部结构特征经过通道数为128的卷积层、两个堆叠的分组卷积模块以及通道数为512的卷积层逐步提取高层次的局部结构特征。由于图注意力模块输出的低层级局部结构特征维数较低，因此第一个卷积层不使用分组卷积。在随后的两个分组卷积模块堆叠能够有效提取高层次特征，并减少卷积层的参数量。

第四部分，输入点云具有无序性，因此使用MaxPool作为对称函数提取排列不变性的全局特征。全连接层由一个具有256个节点的隐藏层和40个节点的输出层组成，并与Softmax层构成的分类器，对全局特征进行分类得到点云所属类别的概率输出。

2.2 图注意力模块设计

本文设计的图注意力模块输入为原始点云X={xi∈R3,i=1,2,…,N}以及采样点云X′={xj∈R3,i=1,2,…,M}，输出为点云的局部结构特征，其中N为原始点云数，M为采样点云数。使用K-NN图G=(V,E)表示点云的局部结构，其中V表示所有图的节点集合，E表示所有图的边缘集合；使用采样点xj作为图的节点，并且根据每个采样点xj的K近邻点xji生成图的边缘eji，边缘eji=xj-xji，xji表示在采样点xj处使用K近邻(K-NN)算法从原始点云xi中搜索到的近邻点。K-NN图结构如图3所示。

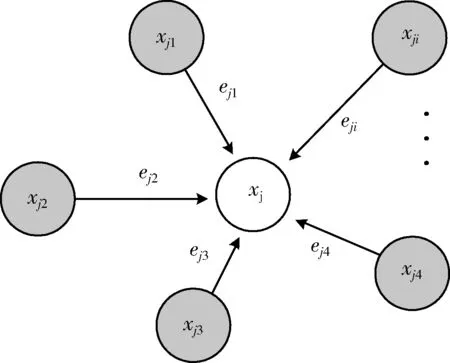
图3 K-NN图结构

如图4所示，使用特征矩阵表示K-NN图输入和输出，K-NN图的输入为N×1×3维的原始点云以及M×1×3维的采样点，输出为M×K×3维的图边缘。为了增强局部结构特征的表达能力，使用注意力机制来突出不同K近邻点的边缘特征的重要性。

图4 图注意力模块

注意力系数由以下几个计算步骤得到。首先，使用卷积核大小为1×1的卷积层提取K-NN图的节点和边缘的高维特征，其计算公式如下

x′j=R(B(Conv{xj,θ}))

(1)

e′ji=R(B(Conv{eji,θ}))

(2)

其中，R为非线性激活函数Relu，B为批次归一化，θ为卷积层的权重。卷积层的输出通道数为F时，计算得到的节点和边缘特征维数分别为M×1×F、M×K×F。其次，使用输出通道为1的卷积层对节点和边缘特征计算得到节点xj的自注意力系数和邻域注意力系数，并将其融合，其计算公式为

bji=LR(R(B(Conv{x′j,θ}))+R(B(Conv{e′ji,θ})))

(3)

其中，LR为非线性激活函数LeakyRelu。最后，使用Softmax函数对bji进行规范化处理，计算公式为

(4)

通过以上几个步骤得到边缘特征的注意力系数aji，其维数为M×1×K，并将其与边缘特征向量e′ji进行矩阵乘法计算得到局部结构特征x″j，计算公式为

(5)

本文设计的图注意力模块具有以下几个优点：①相比使用原始点云中的所有点作为图的节点，使用采样点作为图的节点能够减少大量冗余的局部结构信息，并降低了计算复杂度以及提高网络模型的计算速度；②使用注意力机制对K-NN图的边缘特征进行聚合，为每个边缘特征都分配一个注意力系数，能够自适应学习不同K近邻点的边缘特征对局部区域的重要性，从而减少噪声点的干扰以及增强局部结构特征的表达能力。

2.3 分组卷积模块设计

本文设计的分组卷积模块由特征通道分组、分组卷积层、特征融合、特征通道混洗组成，旨在能够提取高层次局部结构特征的同时减少卷积层的参数量。

分组卷积模块如图5所示，该模块输入特征的维度为M×1×Fin，输出特征的维度为M×1×Fout，其中M、F分别表示点云数量、相应的特征通道。首先，输入特征被划分为特征通道数相等的两条支路，第一条支路的特征使用分组卷积层进一步提取更深层次的特征，第二条支路的特征则直接与第一条支路输出的特征按照通道拼接的方式进行融合。其次，将融合后的分组特征进行特征通道混洗，以加强分组特征之间的信息交流。

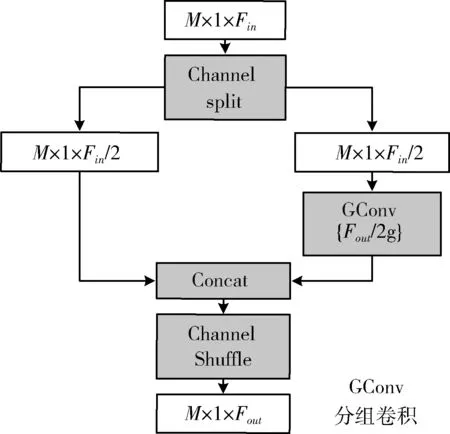
图5 分组卷积模块

分组卷积模块输入和输出特征的通道数相等，其参数量以及计算复杂度的计算公式如下所示

(6)

(7)

由以上公式可知，分组卷积模块与没有使用分组卷积的卷积层相比，当特征提取支路的特征通道划分为g组时，其参数量和FLOPs减少了1/4g。分组卷积模块总共进行了两次特征分组，极大减少了卷积层的参数量。由于过多的分组使得每一组输出的特征只与输入特征相应的分组特征有关，分组特征之间没有信息交流会导致提取的特征表达能力不足。因此将融合后的分组特征通过通道混洗的方式，可以让分组特征获得所有来自不同组的特性信息，使其在下一层级特征分组时分组的特征具有更丰富的信息。此外，在第一次分组中，将一条支路的分组特征采用特征复用方式与另外一条支路提取的特征进行融合，以增强相邻层之间的特征。

3 实验结果与分析

为了验证本文所提出算法的有效性，实验从以下两个方面进行分析：①进行消融实验，全面分析本文网络模型的不同组成部分对实验结果的影响；②将本文提出的方法与当前主流方法分别从识别准确率、时间和空间复杂度以及鲁棒性3个方面进行详细比较。

实验环境。本文实验所采用的硬件环境为Intel Xeon E5-1650、GTX 1080Ti GPU，软件环境为Ubuntu14.04、Python2.7、Tensorflow1.7。

数据集。采用普林斯顿大学公开的数据集ModelNet40，这个数据集是当前三维点云识别主要采用数据集。ModelNet40数据集总共有12 311个三维模型，分为40个类别，如杯子、书架、椅子、汽车等，将数据集划分9843个用于训练，2468个用于测试。每一个模型均被均匀采样1024个点并归一化到单位球中，每个点使用三维坐标(x,y,z)表示。

实验参数设置。本文实验采用交叉熵作为损失函数；网络使用ADAM优化器，学习率为0.001，批次大小为32，Epoch=250，批次正则化率为0.5。采样点数M为512；图注意力模块中的K近邻点取值为20，特征维数F取值为16。输入的点云通过旋转、缩放、抖动的方法实现数据的扩增。

3.1 消融实验分析

在相同的实验条件下使用ModelNet40数据集进行消融实验，分析采样点数、图注意力模块、分组卷积模块以及全连接层分别对网络模型性能的影响。

3.1.1 采样点数分析

本节实验分析采样点数对网络模型的识别准确率、识别时间以及计算复杂度的影响。在表1中，采样点数1024表示原始点云数量，计算复杂度使用十亿次浮点运算量(giga floating point operations，GFLOP)来评估。从表1可见，随着采样点数的减少，网络模型识别一个点云模型的时间和计算复杂度也逐渐减少。采样点数512与1024相比，网络模型的识别准确率提高了0.42%，识别速度提高了42%，计算复杂度降低了50%。但采样点数低于512时，获取的局部结构特征不足，使得识别准确率下降。实验结果表明，本文使用FPS从原始点云中选取一定数量的采样点作为K-NN图的节点，能够获取更有效的局部结构信息，从而能提高网络模型的识别准确率和识别速度，并且能够大幅度减少模型的计算复杂度。

表1 采样点数对网络模型性能的影响

3.1.2 图注意力模块分析

本节实验分析本文所设计的图注意力模块对识别准确率的影响。实验分别从K-NN图中的K值选取、聚合边缘特征的方法以及移除图注意力模块进行分析。如表2所示，K个近邻点分别取值为10、20、30、40得到相应的识别准确率，当K为20时识别准确率最高，表明在K=20时图注意力模块可以更好获取局部结构特征。

表2 K近邻点数对识别准确率的影响

本节实验分别使用注意力机制、最大值池化、求和池化来聚合K-NN图的边缘特征，对应的识别准确率见表3。实验结果表明，本文采用注意力机制聚合K-NN图的边缘特征，通过在局部区域内不同K近邻点的边缘特征分配一个注意力系数以突出不同边缘特征重要性的同时减少噪声点的干扰，能够增强局部结构特征的表达能力，从而获取更高的识别准确率。

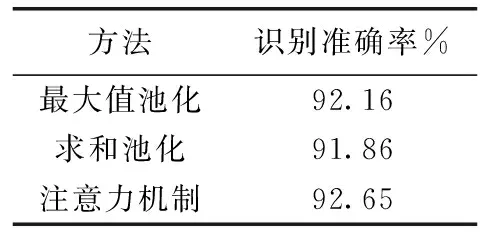
表3 不同边缘特征聚合方法对识别准确率的影响

最后，移除最远采样法和图注意力模块后的网络识别准确率为89.6%，相比未移除前的网络识别准确率低了3%。实验结果验证了图注意力模块能够获取点云的局部结构特征，从而提高网络模型识别细粒度特征的能力。

3.1.3 分组卷积模块分析

本节实验分析分组卷积模块使用不同的分组数对网络模型识别准确率和参数量的影响。每个分组卷积模块的输入和输出通道数均为128。分组数g=0表示不使用分组卷积模块，而是直接使用通道数为128的卷积；分组数g=1表示分组卷积模块只进行一次分组，分组卷积支路的卷积层输出通道数为64；分组数g=2表示分组卷积支路的特征均匀的分为两组。从表4中可知，与不使用分组卷积模块相比，使用分组卷积模块只进行一次分组时，网络模型的识别准确率提高0.17%且参数量更少。然而，随着分组卷积支路的分组数增大，模型参数量逐渐减少，但识别准确率变低，这也说明了特征通道数过小会使得每组的特征信息量不足。

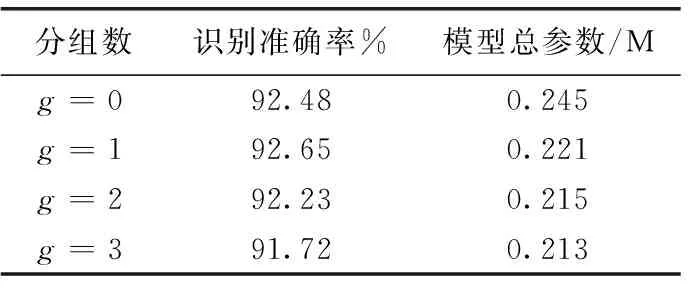
表4 不同分组数对网络模型性能的影响

3.1.4 全连接层分析

全连接层是网络参数集中的地方，所占总参数的比例较高。主要原因有两点：①输入到全连接层的特征维数高；②全连接层的层数与每一层的节点数过多。本节实验为了能够降低网络模型的参数量，在保证网络模型取得较高识别准确率的情况下选取最佳的全局特征维数和全连接层参数。如表5所示，全连接层在输入全局特征维数为512，具有节点数为256的单层隐藏层，网络模型获取最高的识别准确率。实验结果表明，过高的全局特征维数以及更多的全连接层数和节点数并不能有效提高网络的识别准确率，反而会增加网络的参数量。因此，全连接层的输入全局特征维数设置为512，单层隐藏层的节点数设置为256。

表5 全连接层的参数对识别准确率的影响

3.2 对比实验分析

3.2.1 识别准确率对比分析

在ModelNet40数据集上将本文所提的LPCR-Net与当前一些主流方法进行比较，利用平均准确率和总体准确率来评估网络模型的识别性能。如表6所示，本文所提出的LPCP-Net与采用局部结构多尺度特征的Point2Sequence相比，总体准确率相当，但平均准确率低了0.6%；与采用多层级局部结构特征的PointNet++和DGCNN相比，总体准确率分别提高了1.9%和0.4%；与没有利用点云的局部结构特征的LightPointNet和PointNet相比，总体准确率分别提高了3.1%和3.3%，这表明LPCP-Net充分利用局部结构特征能够有效获得点云更为全局的特征描述，从而大幅度提高了网络的识别性能。实验结果表明，本文所提出的LPCR-Net在识别准确率上仍能达到当前主流方法同等或者更优水平。

表6 ModelNet40数据集上的识别性能对比

3.2.2 时间和空间复杂度对比分析

本节实验使用ModelNet40数据集将所提出的LPCR-Net与当前具有代表性方法的时间和空间复杂度进行对比分析。时间复杂度通过训练时间和测试时间进行评估，测试时间为网络模型识别测试集2468个样本的总时间。空间复杂度通过训练完成后所保存模型的大小进行评估。以下实验结果均在本文所搭建的软硬件环境平台下根据原作者公开的源代码进行实验所得。由于Point2Sequnce和PointNet++训练时所占用的显存过大，为了保证在相同条件下进行对比，因此将不同方法的批次输入均设置为10。如表7所示，LPCR-Net的训练时间为1.7个小时、测试时间为3.2 s，明显优于其它主流方法；与PointNet++、Point2Squence和DGCNN相比，LPCR-Net的网络模型参数量分别减少了84.7%、87.8%和87.8%。PointNet使用两个空间变换网络分别实现数据和特征的对齐，空间变换网络由多个卷积层和全连接层构成，因此该网络的参数量最高。PointNet++使用多层级的结构提取点云的局部结构特征，每个层级都均用多层卷积计算，导致模型参数量高。DGCNN的每个层级都需要在特征空间中计算高维特征之间的距离，使得该网络的计算复杂度较高，训练时间长。Point2Sequnce采用多尺度的结构，其计算复杂度最高，训练时间和测试时间最长。然而，本文提出的LPCR-Net使用计算复杂度较低的图注意力模块来获取有效的局部结构特征，并且使用分组卷积来减少卷积层的参数以及优化了全连接层的参数，使得网络模型的时间和空间复杂度远低于以上几种主流方法。实验结果表明，本文所提出方法的网络模型具有时间和空间复杂低的优点。

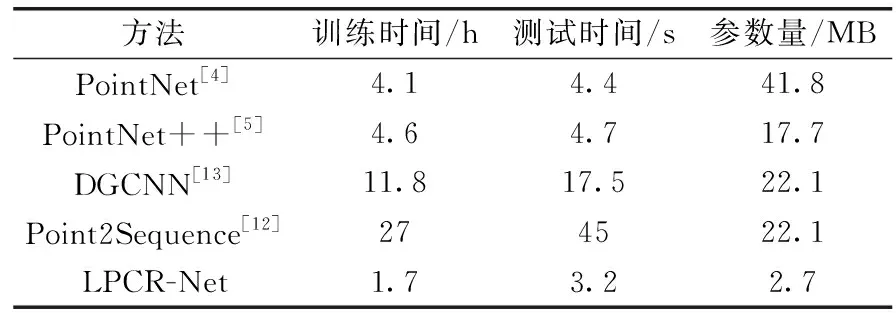
表7 不同方法的时间和空间复杂度对比

3.2.3 鲁棒性对比分析

本节实验分析本文方法对输入点云数量大小的鲁棒性，并与当前主流方法进行对比。如图6所示，LPCR-Net的识别准确率随着输入点云数量减少而降低，在1024个点时识别准确率最高，在1024与256个点之间缓慢下降，但在256个点仍能达到91%的识别准确率；与PointNet++相比，鲁棒性相当，但总体识别准确率更优；DGCNN和PointNet的鲁棒性较低，当输入点云数量低于512时，其识别准确率大幅大降低。实验结果表明，本文方法的识别准确率和鲁棒性都保持较高水平。

图6 不同方法的鲁棒性测试

4 结束语

本文针对当前三维点云识别方法的时间和空间复杂度高的问题，提出一种轻量级的三维点云识别方法。该方法提出的图注意力模块能够充分地提取点云的局部结构特征，并且能够大幅度降低计算复杂度。另外，引入分组卷积提取高层次的局部结构特征的同时减少卷积层的参数量。此外，在保证网络模型取得较高识别准确率的情况下减少全连接层的层数与节点数，以减少全连接层的参数量。实验结果表明，本文方法的识别准确率达到当前主流方法同等或更优水平，并且网络模型的时间和空间复杂度大幅度降低，同时保持较高的鲁棒性。