基于通道剪枝和量化的卷积神经网络压缩方法

徐 晓，蒋志翔，张 杨

(中国航天科工集团第二研究院706所，北京 100854)

0 引 言

辅助维修技术是一种电子的实时维修指导过程，能够提高操作者的作业准确度和维修效率。这一技术在维修过程中将计算机提供的维修指导信息，通过手机、AR眼镜等一系列设备实时叠加到操作者的视野中，给予实时的维修指导。目前辅助维修中的物体识别技术，使用的算法通常为模板匹配和特征点检测，这两种方法在目标简单的应用场景中效果很好，但在实际工程应用时面对机箱、配件等复杂的目标物体，同时出现环境因素的干扰时，如光照、遮挡、阴影等，特征点的检测以及模板与目标物体的匹配度都会受到很大的影响，导致识别精度不高。

随着卷积神经网络技术的不断发展，其在计算机视觉领域取得了很好的识别效果。计算机硬件性能的提升使得高性能图形处理单元被大规模的应用到神经网络的训练中，其具有的并行计算的能力能够快速训练其中的参数，新的深度神经网络框架也不断被提出。但是，随着神经网络框架的深度和尺寸的增长，其参数规模和计算时间也在成倍增加，这已经成为了神经网络向嵌入式平台发展的阻碍，在实际工程应用过程中受到了很大的限制。为了在嵌入式平台上部署神经网络，研究者们也提出了很多方法对深度神经网络进行简化，如HAN S等提出的神经网络压缩方法[2]、谷歌提出的轻量级的神经网络结构Mobile Net[3]等，他们在神经网络的冗余结构、卷积层设计、模块化和激活函数等方面都进行了一定的优化。

这些应用于嵌入式平台的轻量级卷积神经网络，虽然相较于深度神经网络极大地降低了网络的计算量，但是仍难以满足工程中的实时性需求。因此，本文提出了一种基于通道剪枝和量化的综合卷积神经网络压缩方法，压缩网络结构与参数矩阵，提升神经网络的计算效率，满足辅助维修技术在实际工程中的应用需求。

1 设计流程

为实现辅助维修中的实时物体识别任务，提升其在嵌入式平台上的实时性，以将其部署在例如手机、AR眼镜等资源有限的移动设备中。本文提出了如下的方案设计流程。对训练好的神经网络进行一定程度的压缩，使其识别精度保持在一定水平的情况下，降低网络的结构复杂度，减小参数矩阵，降低其占用的存储空间，设计流程如图1所示。

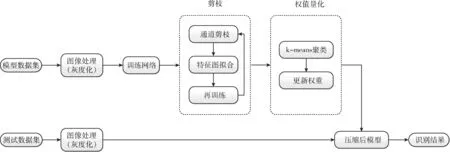
图1 卷积神经网络压缩流程

在神经网络的训练阶段，①需要创建可供网络进行训练的数据集。在已有模型数据集的基础上，对其进行处理，剪裁、翻转、添加光影效果等操作可以扩大数据集的容量，灰度化操作可以避免模型纹理和颜色产生的训练误差。②使用处理后的数据集对网络进行训练，获得训练好的原始网络。③对神经网络进行通道剪枝操作。首先，添加L1/2范数对权重矩阵进行约束，稀疏矩阵使得大部分的权重值为0。同时，在剪枝过程中使用最小二乘法对剪枝后特征图与原特征图进行拟合，删除对网络影响较小的通道。然后，对剪枝后的网络进行再训练，恢复保留连接的权重值。实现对神经网络结构的精简及计算的加速。④对剪枝后的权重进行k-means聚类，采用每个聚类的中心值作为类内共享权重值，减小权重所需的存储空间，实现神经网络占用存储空间的压缩。

在神经网络的测试阶段，对测试数据集进行灰度化处理，减少纹理和光影等产生的识别误差。使用压缩后的模型对处理后的数据集进行测试，得到最终的识别结果。

2 卷积神经网络通道剪枝策略

2.1 通道剪枝策略

剪枝是对卷积神经网络结构进行精简的有效方式，可以有效的对其进行压缩和加速。剪枝操作主要有非结构化剪枝和结构化剪枝两种。非结构化剪枝操作使用阈值判断神经元之间的连接是否有效，对失效的连接进行剪枝，这种剪枝策略在理论上具有较高的神经网络加速能力，但由于剪枝操作可以应用于任何一个神经元节点，导致剪裁后的神经网络形状不规则，不利于实现。结构化剪枝则是对整个卷积核进行剪枝，从大型矩阵中消除整个行或者列。通道剪枝也是结构化剪枝中的一种，通过对通道的剪裁，直接减少特征图的映射宽度，缩小网络结构，同时保持各个卷积层形状的统一，不但能够很好压缩网络结构，还能减少大量矩阵运算所消耗的计算时间。

图2所示的就是本文提出的通道剪枝策略。图中所示的矩阵A表示原始的输入特征图，矩阵B表示原始的输出特征图，矩阵A’ 表示剪枝操作后输入的特征图，矩阵B’ 表示剪枝操作后输出的特征图，W表示维度为c×kh×kw卷积核，卷积核的个数为n，kh和kw表示卷积核的大小，c表示特征图A的通道数，其中

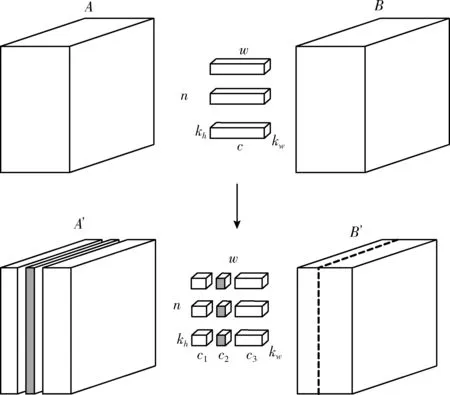
图2 通道剪枝策略

c1+c2+c3=c

(1)

通道剪枝的目的是对特征图A中的冗余通道进行剪裁，删除学习特征较少的特征图，减少网络的整体计算量。对A中的通道进行剪裁，相当于对卷积核W中与冗余通道对应的卷积核进行剪裁。卷积神经网络在图像识别任务中需进行大量的矩阵计算，减少卷积核的个数可以极大地减少网络中的矩阵计算次数，显著减少网络的计算时间。

对于给定训练集图像

D={(x1,y1),(x2,y2),…,(xm,ym)},xi∈R,yi∈R

假设其输入数据是H×W×C的三通道图片，由大小为k×k的卷积核对其进行特征提取操作，可以得到大小为H′×W′的特征图。当步长为1时

H′=H-k+1

(2)

W′=W-k+1

(3)

在第l个卷积层具有Sl个卷积核，输入为Hin×Win×Cin的特征图，则该层能得到大小为Hout×Wout×Cout的特征图。那么，模型中单个卷积层的时间复杂度为

T～O(Hout×Wout×k2×Cin×Cout)

(4)

卷积神经网络的整体时间复杂度为

(5)

可见，卷积神经网络的时间复杂度由输出特征图的大小、卷积核大小及输入输出通道数决定。因此，对卷积神经网络中的通道数进行剪枝能够极大地减少模型的时间复杂度，对模型的计算时间进行加速。

剪枝操作需要选择出对神经网络识别性能影响最小的通道，对其进行删除。在神经网络结构中，删除一个卷积层中的通道可能会显著改变下一层的输入，导致剪枝带来的误差逐层传播，所以在剪枝时需要对通道进行选择衡量，以保证删除的通道是冗余的，对网络的识别精度影响不大。

对于给定的训练集,Xi表示第i个输入，Yi表示第i个输出，Wi表示第i个卷积核。那么，神经网络的损失函数为

(6)

为对需要剪枝的通道进行选择，给定一组向量β={β1,β2,…,βm}，对其进行求解，βi的取值为0或1。βi是判断该通道是否要进行剪裁的一个向量，当βi的值为0时，则意味着需要对该通道进行剪裁。通道选择问题就是向量β的求解问题，因此转化为式(7)的优化问题

(7)

其中，W表示维度是n×c×kh×kw的卷积核，所以n表示的就是输出特征图的通道数；X表示输入的m个维度为c×H×W的训练样本。因此当卷积核W与输入样本X进行卷积时，得到的就是大小为(W′×H′)×n的输出Y，W′和H′为每个特征图的长乘以宽。因此，相当于把二维的特征图转换为一个向量，这样也得到了一个二维的输出Y。

但是，上述优化问题的公式是无法直接求解。为得到向量β的最优解，在公式中添加正则子对β进行约束，正则子也称为范数，不同的范数会导致不同的求解结果。L0范数表示的是数据中非0元素的个数，它的稀疏化结果能使参数的非零元素最少，但是由于L0范数难以求解，是一个NP难问题，因此难以应用在算法的求解问题上。L1范数表示的是向量中各个元素绝对值之和，也叫“Lasso回归”(Lasso regularization)，它不仅能得到与L0范数近似的稀疏化结果，而且比L0范数容易求解，因此得到了很好的应用和发展。L2范数也叫“岭回归”，它能够很好改善网络的过拟合问题，但是对不能对数据进行很好的稀疏。

本文提出的通道剪枝算法中，为了能得到比L0范数容易求解同时比L1范数更为稀疏的正则化结果，提出使用L1/2范数对所求的公式正则化。L1/2范数是向量各元素绝对值根号和的平方，其在求解过程中的回归速度比L1范数更快，而且能得到更稀疏的正则化结果。因此，关于β求解公式为

(8)

其中，正则参数λ用来对向量β中非零值的数量进行控制，λ越大，β中的非零值越少，这样网络结构的压缩率也越大。对此公式不断进行迭代优化，直到向量β中非零值的数量满足通道剪枝的需要。

2.2 最小二乘法拟合特征图

剪枝操作在删除网络结构冗余通道的过程中，会导致原始网络训练出的特征图发生损失，特征图损失增加的误差使得网络的识别精度降低。为了在精简网络结构的同时仍然保持网络原有的识别精度，需要在剪枝过程中对特征图进行拟合，使得剪枝后的网络特征图与原始网络之间的差异尽可能的小，保留神经网络学习到的图像特征信息。

在进行通道选择时，使用了向量β对其进行约束，通过不断的迭代优化对向量β的取值进行了更新，但以剪枝数量为目的的选择会显著降低网络的识别精度。为在剪枝的同时减少特征图的损失，本文使用最小二乘法优化向量β，通过迭代计算最小化剪枝后网络输出的特征图与原始特征图之间的误差，达到较优的剪枝效果。对向量β进行更新的公式如下

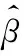
3 权值量化

在对神经网络进行了剪枝操作后，网络中只保留了对网络影响重要的权值，为了进一步减少权值占用的存储资源，需要对其进行量化压缩，通过让值相近的权重共享同一权值，实现网络压缩的目的。使其在保证神经网络识别精度的同时，不但加快计算效率，还减少所需的存储空间。

为实现权重量化，对神经网络中的权重进行k-means聚类。设所需的聚类数量为k，则需要log2k个比特位来对该类进行表示，然后采用每个聚类中心点的值作为该类内共享的权值。这样，只需要对每个权重所属的类别进行存储，每一类占用log2k个比特，以及每一类的中心点的值，大大减少了存储的数值量。k-means聚类的公式为

(10)

其中，W={w1,w2,…,wn}为n个原始权重的集合，C={c1,c2,…,ck}是将原始权重划分为的k个类，对向量C进行求值使得每个类内的平方和最小化。如图3所示。

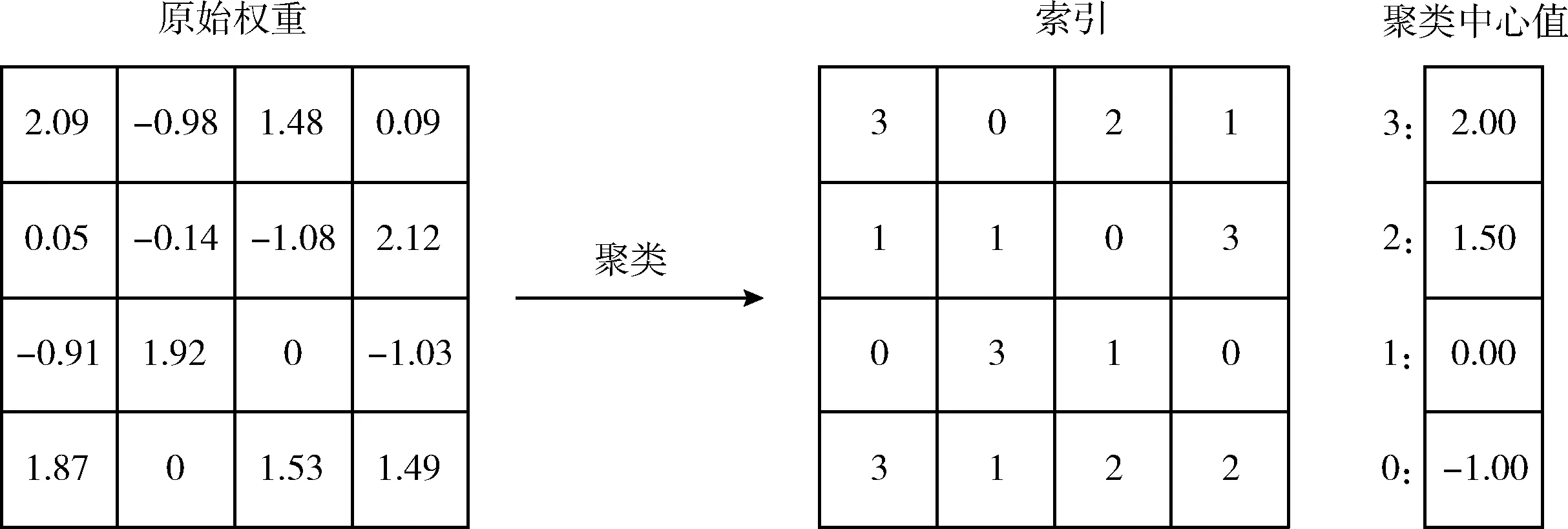
图3 k-means聚类过程

4 实验和结果分析

为验证本文提出的基于通道和量化的综合卷积神经网络压缩方法，在嵌入式平台上实现实时目标机箱识别任务的可行性，以及该方法对神经网络的加速能力。以物体识别正确率P、神经网络压缩率及每秒处理的图片帧数fps作为评价指标，嵌入式平台(CPU为Snapdragon 845,GPU为Andreo 630)作为测试平台，基于Keras框架对Mobile Net V3及压缩后的网络进行实验，对其识别性能进行评估。

4.1 训练数据集

本文使用的数据集由公共数据集Pascal Voc中的部分数据及目标机箱数据组成，以验证本文提出神经网络压缩方法的有效性及在辅助维修实际应用场景中的实时性。Pascal VOC数据集是一套计算机视觉的标准数据集，从中提取出与应用场景相关的训练数据，如桌子、椅子、电视、电脑等类别。同时，以标准数据格式增加目标机箱数据，对神经网络进行训练及测试。

为扩充数据样本，本文使用了Imgaug图像处理库对样本图像进行处理，主要处理技术包括两大类：空间几何变换和像素颜色变换。空间集合变换是对图像进行翻转、剪裁、旋转、缩放、形变等操作。像素颜色变换是叠加噪声、图像模糊、对比度变换、颜色扰动、随机擦除、超像素法、锐化和浮雕等。在样本数据中覆盖在实际场景中可能覆盖的特征要素，如光照、遮挡、倾斜等。如图4所示的是部分数据集的图像样本。

图4 机箱数据集图像样本

4.2 神经网络压缩结果分析

MobileNet V3是谷歌发布的轻量级神经网络结构，分为大小两种版本，大版本具有20层结构，包含了4个卷积层、1个池化层和15个MobileBlock块结构，参数量为5.4 M。小版本具有16层结构，包含了4个卷积层，1个池化层和11个MobileBlock块结构，参数量为2.9 M。轻量级的神经网络结构原始的参数大小相较于深度神经网络已经减少了很多，删除了参数量较大的全连接层，但是其在嵌入式平台上还是难以保证物体识别的实时性，因此可以采取神经网络剪枝和量化策略进一步的减少其中的冗余结构，实现对结构和参数的压缩。

对MobileNet V3 Large神经网络结构进行压缩，以物体识别正确率P、神经网络结构的压缩率作为评价指标，验证本文提出的基于通道的综合网络压缩方法的有效性。

物体识别正确率P，以物体识别精度IoU为基准进行定义。IoU是模型所预测的检测框和真实检测框的交集和并集之间的比例，如图5所示。

图5 物体识别精度IoU

物体识别精度IoU的定义如下式

(11)

目标物体的大小对识别精度IoU的影响较大。在识别像素值较小的物体时，相等预测检测框偏移量会导致IoU的取值较低。在本文的辅助维修场景中，主要面向机箱面板进行识别，在识别完成后与建立好的面板模型进行匹配，因此训练集中的目标物体像素值都在80×100以上。当偏移量在8像素以内时，IoU的取值约为80%。因此，规定当IoU大于80%时，视为物体识别正确；当IoU小于80%时，则视为识别错误。定义物体识别正确率P为

(12)

其中，T为测试集的数据总数，T′为识别正确的数据总数。

同时，定义压缩率c如下式

(13)

其中，W为原始参数量，ΔW为减少的参数量。

压缩率的大小会影响神经网络的物体识别精度，随着对神经网络结构中通道的剪裁，神经元节点的连接情况和参数矩阵也在不断改变。如图6所示的是压缩率对识别正确率的影响。从图中可以看出，随着压缩率的不断上升，其识别正确率在逐渐下降，在压缩率为0.7时，神经网络的识别精度并没有显著下降，可以满足辅助维修的现场作业精度需要，精度为92.4%。但如果进一步压缩网络，则会导致网络学习到的特征向量被破坏，出现识别精度的显著下降，无法满足应用需求。

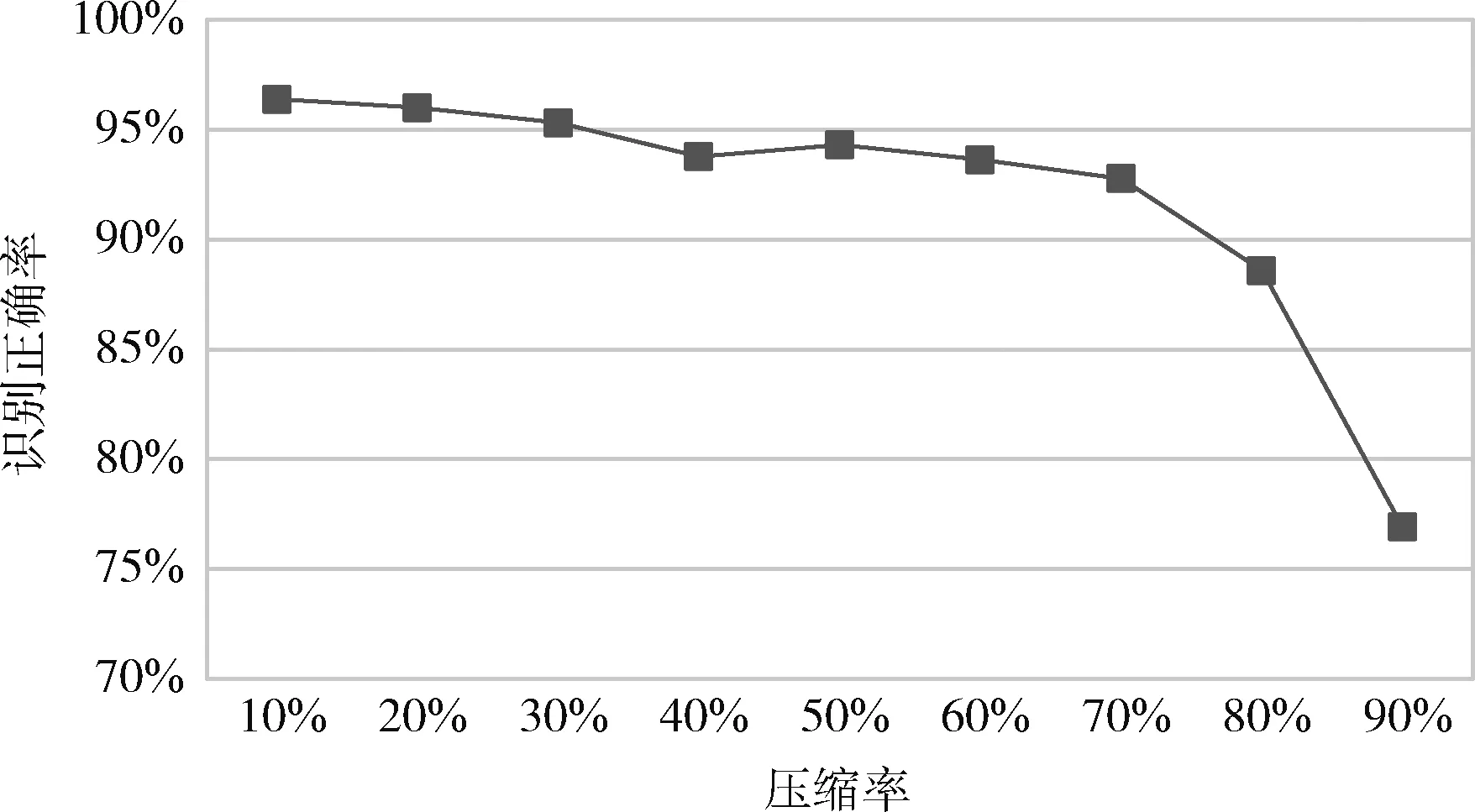
图6 神经网络压缩率对识别精度的影响

表1中对各个神经网络结构的剪枝压缩率都为70%，从表中可以看出，3种轻量级网络的原始参数大小在几兆，在压缩和量化后可以显著减小参数矩阵所占用的存储空间，减少网络的计算量。

表1 神经网络压缩结果

在对网络结构进行压缩后，3种轻量级网络和VGG-16的识别精度都产生了一定程度的下降。深度神经网络VGG-16的原始识别精度最高为98.8%，但在压缩后低于MobileNet V3-large的精度，可见结构复杂的深度神经网络结构可以学习到更多的图像特征，由于其参数矩阵的庞大且相对稀疏，在进行通道剪枝操作时，会由于网络的稀疏性剪裁掉部分特征数据，导致识别精度的下降。MobileNet V3-large的识别精度相较于原始网络降低了4.2%，可见通道剪枝策略能够有效剪裁掉冗余数据，实现参数矩阵的低损压缩。

4.3 神经网络运算速度

为对压缩后的神经网络运算速度进行测试，以物体识别正确率P及每秒处理的图片数量fps作为评价指标，验证本文提出的基于通道的综合网络压缩方法对于神经网络运算速度能力提升上的有效性。

神经网络在对图像进行处理时，所需的大量时间都集中在参数矩阵的卷积计算中，GPU所具有的并行计算能力，能够极大加快参数矩阵的计算速度。在对神经网络结构进行压缩后，参数量大大降低，减少了神经网络所消耗的计算资源，提高了数据处理速度。

表2所示的是神经网络压缩对运算速度。以人眼的可视帧数达到每秒24帧就可以捕捉到不闪烁的画面，满足实时性的需求为基准。在压缩前，轻量级网络MobileNet V3-small的识别速度能够达到37 fps，满足物体识别任务实时性的要求，但是其识别正确率与MobileNet V3-large相比低了12.7%，识别能力差距很大。在对网络进行压缩后，MobileNet V3-large达到了26 fps，满足了实时性的需求，同时其识别正确率保持在90%以上，可以满足辅助维修的工程应用需求。可见本文提出的神经网络压缩方法对神经网络在嵌入式平台上的部署，以及实现实时物体识别能力提供了较为有利的支撑。

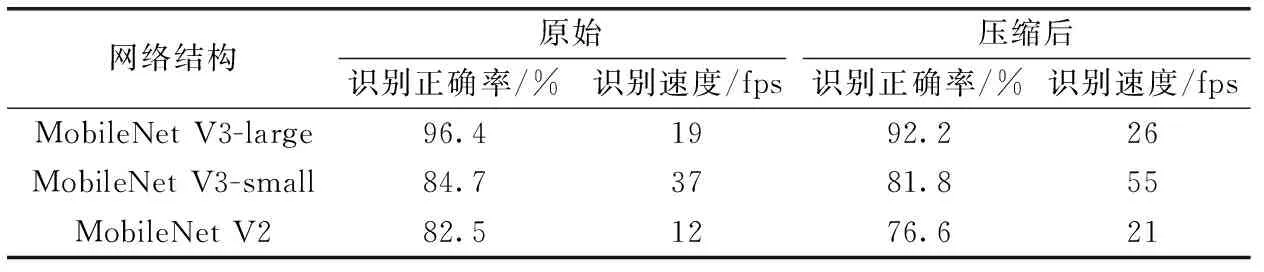
表2 神经网络运算速度

4.4 机箱数据集识别效果

在辅助维修任务中，需对视野内的机箱面板进行识别，以进行模型对准工作，为进一步的向操作者提供辅助的电子维修信息。使用机箱数据集对轻量级神经网络MobileNet V3-large进行训练，并压缩其网络结构，将其部署在嵌入式平台，进行机箱数据集识别效果的验证。验证结果如图7所示，可以看出场景中的机箱面板存在光照、相似背景干扰的影响，但是神经网络准确的对其进行了定位同时正确的将其分类。可见本文提出的神经网络压缩方法在实际工程应用的数据集上也得到了很好的验证。

图7 机箱数据集识别效果

5 结束语

随着人工智能时代的到来，越来越多的领域都在尝试使用神经网络去解决智能任务，神经网络的发展不能只停留在台式机、服务器上，也需要在诸如手机、平板、AR眼镜等一系列移动设备上进行部署使用。目前，大多数的深度卷积神经网络模型都因为尺寸太大而不能很好应用于移动端，一些已提出的轻量级神经网络也难以在计算资源有限的嵌入式平台上满足实时性的要求，因此对神经网络模型进行压缩和加速是非常具有意义的研究方向。

本文针对卷积神经网络的压缩方法进行了一定的研究，并对神经网络卷积层的通道剪裁算法进行了优化，通过一系列的实验结果，验证了本文算法在神经网络的压缩率、识别精度和处理速度上都有了一定的提升。首先通过对神经网络的权重使用L1/2正则子进行约束，以稀疏的权重矩阵指导每层神经网络的剪枝策略。同时，使用最小二乘法在剪枝过程中对特征图进行拟合，保证其不变性。最后，通过k-means聚类算法，将权重进行压缩存储。

本文对神经网络结构的压缩算法做了探索性的研究，使其具备了在嵌入式平台进行辅助维修的实时性。在实际应用过程中，本文识别的目标物体为机箱面板，然后使用已知面板模型与其进行匹配，定位面板上的其余细小部件。机箱面板的像素值较大，识别准确率较高，而本方法在面对小目标，如螺丝、按键等，进行识别时效果不佳，不具备辅助维修过程中的通用性。因此，在后续的工作中，需要进一步对小目标物体的精确识别方法进行研究，再结合实际硬件平台进行部署，实现工程通用性应用的目标。