爆炸场中三波点对冲击波压力测试的影响研究*
2021-11-01徐春冬王良全
徐春冬,王良全
(南京理工大学 机械工程学院,江苏 南京 210094)
0 引 言
弹药爆炸过程中会产生诸多毁伤元,如冲击波、破片、热流、地震波等都会对目标产生一定的毁伤作用,其中冲击波超压大小是其最主要的毁伤参量之一[1]. 在实际工程测试中,传感器的安装位置和三波点的高度会直接影响冲击波超压测试的准确性,因此,研究爆炸冲击波三波点的位置对于准确获取爆炸冲击波超压大小具有非常重要的意义[2].
目前,国内外对于爆炸冲击波三波点位置高度的研究较多,国外对于冲击波的理论研究起步较早. 1974年,美国人Baker[3]对空中爆炸理论及爆炸相似律进行了非常详细的论述,并对空中爆炸实验及参数测试方法进行了研究和总结. 他还指出,冲击波作用到墙体时发生绕射,在此过程中会产生涡流和稀疏波,并对相关实验进行了分析. 1983年,德国人Held[4]对自由场冲击波进行了研究,他指出大药量炸药爆炸产生的自由场冲击波的超压值和正相压力比冲量能用简单的方程近似计算出来,并给出了一些拟合公式. 之后西方国家开始积极地研制温压弹,并进行了深入的研究,其中包括温压弹爆炸产生的冲击波传播规律研究等. 2016年,法德圣路易斯研究所的Ehrhardt等[5]在研究爆炸场冲击波压力预测模型时,利用高速摄影对C-4炸药在5种不同当量(200 g,500 g,1 kg,2 kg,5 kg)和3种爆心高度(33 cm,66 cm,133 cm)条件下的三波点轨迹规律进行了研究,发现随着爆心高度的增加及TNT药量的减小,三波点的轨迹逐渐接近地面,且在三波点轨迹上方测得的冲击波压力曲线会先后出现2个压力峰值,分别为入射压和地表反射压.
近年来,我国对冲击波传播规律的研究取得了较大发展. 段晓瑜等[6]利用AUTODYN软件对含铝炸药的三波点变化规律进行了仿真计算,结果表明,基于爆热当量的经验图表法不适用于含铝炸药三波点高度的计算,而采用数值模拟方法可以获得准确的含铝炸药三波点高度. 谷鸿平等[7]采用数值仿真的方法研究了起爆方式对炸药爆炸冲击波场的影响,研究结果表明,在5倍比例距离范围内,起爆方式可改变炸药爆炸冲击波场的局部分布形态,在不同的方向和距离会对冲击波场产生不同的影响趋势. 郭炜等[8]研究了爆炸冲击波传播过程中三波点的轨迹和在三波点上下不同位置测量结果的区别以及与在地面测量冲击波压力的关系,对比分析了两种测量方法的相对标准差,得到了不同测量方法对测量不确定度的影响. 庞春桥等[9]研究了在一定爆高条件下,高原静爆冲击波参数的计算方法,建立了冲击波参数预测模型并进行了试验验证. 王锋等[10]采用数值仿真的方法研究了侵彻弹爆炸场三波点高度的变化规律,研究结果表明,侵彻弹爆炸场三波点位置高度低于同药量裸装炸药或普通弹药,并随传播距离的增加,侵彻弹爆炸场三波点位置高度逐渐增加. 张学伦等[11]利用AUTODYN软件,对爆炸冲击波传播过程中三波点的轨迹进行了仿真计算,并将计算结果与试验数据进行了比较,发现在中远场的仿真计算结果与实测数据误差相对较小,对于战斗部在一定装药对比高度条件下的三波点高度预测以及冲击波超压测试点的布设具有一定的借鉴意义. 杜红棉等[12]从空中和地面冲击波传播方面分析了近地爆炸冲击波的传播规律并给出了经验公式,根据文献数据拟合仿真出近地爆炸冲击波马赫杆的三维三波点马赫波轨迹图,并通过实测数据和理论仿真结果对比分析验证了空中和地面冲击波传播特性,为冲击波压力的测点布置和数据分析提供了一定的理论依据. 童晓等[13]对不同传感器安装方式与周围流场的相互作用,不同安装方式下传感器敏感面的压力值,以及不同传感器安装方式适用的冲击波压力测量范围进行了仿真分析,设计了一种易于现场安装的楔形传感器安装结构.
本文采用AUTODYN对实测爆炸场环境建立数值模型,在不同位置处设置高斯测点,获取爆炸冲击波压力时程曲线,并对实测自由场压力和地面反射压冲击波数据进行对比,分析了三波点的位置对爆炸冲击波超压测试的影响.
1 爆炸冲击波三波点轨迹
战斗部近地爆炸时,冲击波最早在爆心投影的地面发生正反射,然后以逐渐增大的入射角α0在地面发生斜反射. 根据冲击波强度和入射角,斜反射又分为双波结构的正规反射和三波结构的非规则反射(又称马赫反射). 从整个冲击波的剖面来看,入射波是以爆心为圆心的部分被截去的圆,反射波则是从爆心投影点升起的圆弧,其反射角为α1,这就是正规反射的图像,如图 1 所示. 随着冲击波继续向外传播,当α0大于临界角后进入非规则反射,一个为入射波,一个为与地面垂直的合成波(马赫杆),另一个是与地面成一定角度的反射波,三个波会聚于一点,称为三波点,三波点随着冲击波向外传播逐渐升高,即为马赫反射,如图 2 所示[14].

I—入射波;R—反射波

I—入射波;R—反射波;M—合成波
2 数值仿真模型建立
本文按照实际靶场测试方案进行数值仿真模型建立. 模型中可见空气域的大小为24 m×4 m,TNT装药量为10 kg,形状为圆柱形,其长径比为1∶2,起爆方式为中心起爆,在距离爆心 4 m、6 m、8 m、10 m、12 m、14 m、16 m、18 m、20 m、22 m和24 m处的地表和距离地面3 m的空中设置22个高斯监测点,用于地面反射压力和空中压力的监测. 其中沙土厚度为1 m,空气厚度为4 m,TNT爆心高度为3 m,爆炸场的长度为25 m. 沙土采用材料库自带的SAND材料,基于ALE模型进行计算,炸药采用TNT材料,空气采用AIR材料,二者均基于EULER模型进行计算. 此外,为了模拟真实的爆炸场情况,分别在沙土域的底部和空气域的顶部及左侧施加无反射边界条件,保证冲击波可以流出爆炸场,从而避免不必要的反射. 爆炸数值仿真模型如图 3 所示.
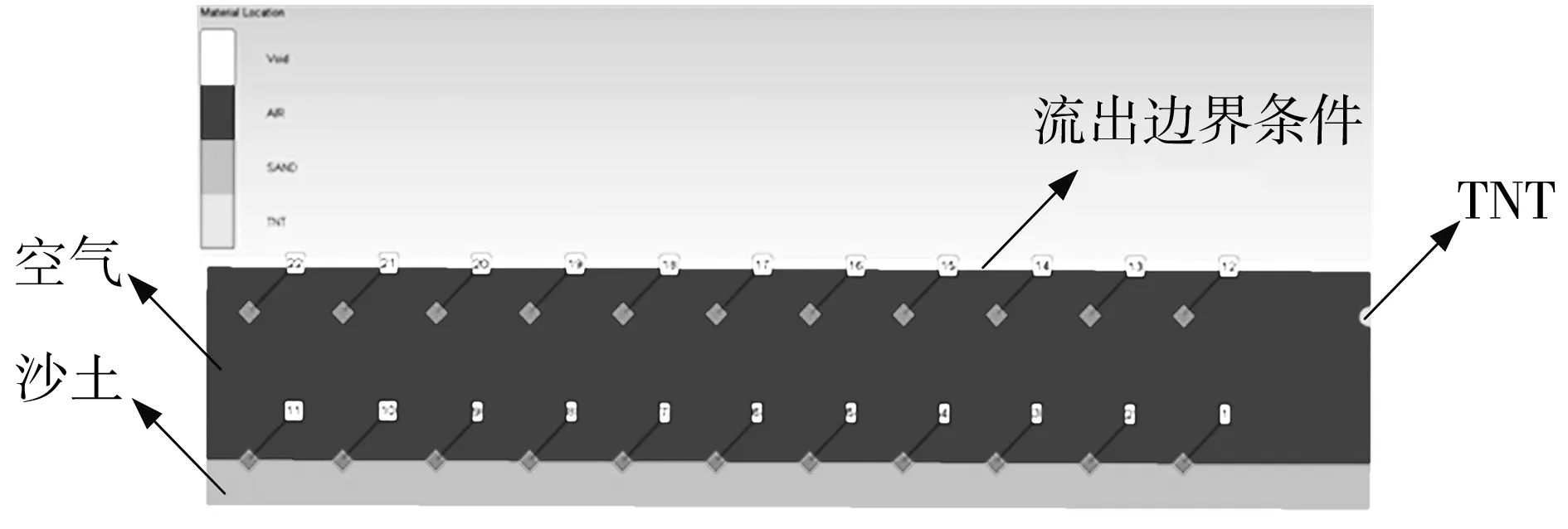
图 3 TNT爆炸场数值仿真模型
在上述模型中,空气为理想气体,密度为0.001 225 g/cm3,E=4.29×106J/kg,JWL状态方程为

(1)
式中:P为压力;V为体积;E为内能;A和B为材料参数;R1,R2和ω为常数参数. 根据实际试验测试研究分析,材料各个参数的具体取值如表1 所示.

表1 TNT中JWL状态方程参数
3 数值仿真结果分析
3.1 仿真数据分析
利用上述模型进行数值仿真,仿真完成后对数据进行提取处理,得到不同测点位置处的爆炸冲击波压力时程曲线如图 4 所示.

(a) 10 kg TNT不同测点处地面反射压

(b) 10 kg TNT不同测点处空中压力
如图 4 所示,在仿真过程中发现同一测点距离下,空中高斯监测点测得的压力比同样地面处的冲击波压力峰值小,在距离爆心8 m处测得冲击波压力存在2个压力峰值,在距离爆心大于 8 m 时测得的压力只有1个压力峰值. 根据上述冲击波压力传播规律的理论分析,可得产生该现象是因为高斯监测点和三波点相对位置的不同所造成的.
当TNT在爆炸场中爆炸时,爆心高度往往有限,三波点的高度随着到爆心距离的增加而逐渐增加. 当监测点位于三波点轨迹之上时,测得的先是入射波压力,后是反射波压力;而当监测点在三波点之下时,测得的则是马赫杆波阵面的压力. 为了验证上述猜想,对仿真结果进行进一步分析,得到了当量为10 kg的TNT爆炸场中马赫杆高度为3 m时(即和爆心处于同一高度)三波点的示意图,如图 5 所示. 由图可知,在该马赫杆高度下,三波点和爆心之间的距离为8.2 m.
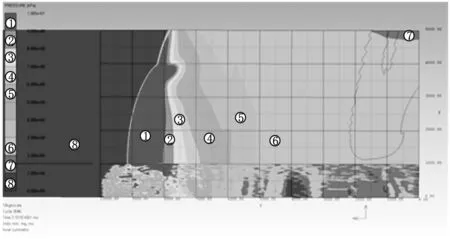
图 5 10 kg TNT三波点示意图
因此,在爆心高度为3 m,TNT药量为10 kg的条件下,当测点和爆心之间的距离小于8.2 m时,测得的压力属于自由场冲击波压力;当测点和爆心之间的距离大于8.2 m时,测得的压力属于马赫杆波阵面的压力. 因此,在这种爆心高度和装药参数条件下,合理的自由场压力测点布设位置应该在距离爆心8.2 m以内.
3.2 实测数据分析
战斗部近地爆炸时相当于半无限空间爆炸,因此,其空中冲击波传播特性与无限空间爆炸冲击波传播特性具有相似的关系. 无限空中爆炸是指弹药在无边界的空中爆炸,这时空气冲击波不受其他界面的影响,即反射波不影响自由场压力[10]. 一般认为,无限空中爆炸时,装药的对比高度应符合

(2)
式中:H为弹药中心距离地面的高度(爆心高度),m;ω为TNT装药当量,kg. 该经验公式的导出是基于点装药的假设,而实际战斗部冲击波超压测试受爆心高度、装药量、外形尺寸、起爆方式、地表材质、战斗部外壳等多种试验环境因素影响. 以某型战斗部近地静爆冲击波超压测试结果为例,某战斗部装药的对比高度为0.64 m/kg3,满足经验公式的无限空中爆炸条件,但实测结果却与冲击波理论传播规律存在一定差异.
在实际测试过程中获得测点距离R分别为13 m、23 m、30 m处的地面和自由场冲击波压力的时程曲线如图 6、图 7 所示.

(a) 13 m处

(b) 23 m处

(c) 30 m处

(a) 13 m处

(b) 23 m处

(c) 30 m处
由于上述冲击波压力时程曲线只能得出冲击波压力传播规律,不能对其进行量化分析,所以,对上述冲击波压力峰值进行提取,得到不同测点位置处的地面和自由场冲击波压力峰值,如表2 所示.

表2 冲击波压力超压峰值
对图 6、图 7 及表2 进行分析可以看出,随着测点距爆心距离的增加,爆炸冲击波超压峰值逐渐减小,峰值的衰减速率并不呈线性关系,具体表现为越靠近爆心,衰减速度越快. 并且当测点在13 m和23 m处时,在同一测点位置上地面反射压大于自由场冲击波压力,符合爆炸冲击波的传播衰减规律;但当测点距离爆心30 m时,自由场冲击波压力大于地面反射压,分析其原因为30 m 处自由场压力传感器位于三波点下方,此时测得的冲击波压力并不只是入射波压力,而是压力叠加之后马赫杆的压力,所以大于同一测点距离上的地面反射压.
对于单一自由场压力测试而言,压力传感器的安装高度会直接影响爆炸冲击波的压力测试,根据上述三波点轨迹位置的分析,三波点的位置随着距离的增加逐渐升高,因此,在架设自由场冲击波压力传感器时,需要考虑自由场冲击波压力传感器的布设高度,使得传感器位于三波点的上方,避免采集得到的数据为马赫杆压力.
对某高能毁伤弹药爆炸时的自由场冲击波压力进行获取,得到的冲击波压力时程曲线如图 8 所示.

(a) 9 m处

(b) 11 m处
图 8(a)为距离爆心地面投影9 m处的自由场压力曲线,压力峰值为0.16 MPa;(b)为距离爆心地面投影11 m处的自由场压力曲线,压力峰值为0.18 MPa. 根据测试数据和压力波形可知,距离爆心较远的测点自由场压力峰值大于近距离测点,出现这一现象的原因在于:9 m处自由场压力传感器位置高于三波点,测得的先是入射波后是地表反射波的双波峰,而11 m处自由场压力传感器位置低于三波点,测得的是马赫波的单波峰.
4 结 论
本文通过AUTODYN对爆炸场冲击波进行数值仿真,对爆炸产生的冲击波曲线及云图进行分析,并对实测数据进行分析. 结果表明:爆炸冲击波三波点高度受爆心高度的影响,并且随测点距爆心距离的增加,三波点的高度逐渐升高,从而导致自由场压力传感器测得的是马赫杆的压力而不是入射冲击波的压力. 因此,在测量自由场冲击波压力时,对于自由场冲击波压力传感器的安装需要考虑传感器的安装高度,确保传感器位于三波点上方,测量冲击波入射波的压力大小. 当自由场冲击波压力时程曲线出现一个波峰时,可按上述冲击波传播规律进行分析解释.
