基于MATLAB的平面度误差评定程序设计

马书红， 吴呼玲， 薛 帅

(陕西国防工业职业技术学院 1. 基础课部; 2. 智能制造学院， 陕西 西安 710300)

0 引言

平面度误差，是指被测实际平面对理想平面的变动量[1]。测量方法有直接测量和间接测量两种，直接测量是指可直接得到平面被测点坐标值或直接评定被测平面度误差的方法。间接测量是指通过测量不能直接得到被测平面上各点坐标值，需经过数据处理才可得到各点坐标值的方法，例如自准直仪法、水平仪法、跨步仪法[1]等。

多数情况下，平面度误差的测量点数较多，数据处理过程较复杂，处理结果的准确性和时效性难以保证，通过计算机程序对其进行处理成了解决问题的关键。本研究从平面度误差评定的三种评定过程进行分析，根据评定过程和评定原理进行程序设计，通过实际的数据计算，验证程序的正确性。通过计算机实现平面度误差的评定，实现了误差处理的准确性和高效率，也为数学建模课程的实际应用奠定了一定的基础。

1 旋转理论评定平面度误差

在平面度误差的测量过程中，调平被测平面很费时间，尤其是被测平面较大时，调平更加困难。因此常采用布线方式，用水平仪测量若干直线上各点，经过适当的坐标转换，将测量数据统一转换为对选定基准平面的坐标值，然后按一定的评定方法确定其误差值。评定方法主要有：三远点法、对角线法、最小二乘法和最小包容区域法。

旋转理论[2]评定平面度误差的过程步骤如下。

(1) 对于一个被测平面的m行n列的测量数据，将每一点的旋转量分解为绕行的旋转和绕列的旋转两个分量。

(2) 设定被测平面绕行的旋转轴为第一行，旋转量分别为：第一行为零，第二行为Q，第三行为2Q，第四行为3Q，依次类推。由于测量的行距相同，所以每一行相对前一行的旋转增量也相同。

(3) 设定被测平面绕列的旋转轴为第一列，旋转量分别为：第一列为零，第二列为P，第三列为2P，第四列为3P，依次类推。由于测量的列距相同，所以每一列相对前一列的旋转增量也相同。

(4) 将每一测量点绕行的旋转量和绕列的旋转量的对应点相加，可得到被测平面上每一测量点的旋转量。将被测平面的m行n列的测量数据与每一测点的旋转量相加，可得到每一测点旋转之后的坐标值。

(5) 选定某一评定方法，按照评定原理，选择对应的目标点，计算出每一点的旋转量，对各测点做坐标换算，得到每一测量点的新的坐标。

(6) 分析旋转后，各测点新的坐标，是否符合某一评定方法的评定准则，如果不符合，则应该做二次旋转，重复以上步骤。

例如：对于一块350 mm×350 mm的平板进行平面度误差的测量和评定，选用千分表进行测量，每测点的行距和列距为100 mm，每行和每列分别测量三个点，利用旋转理论求出其平面度误差。

350×350的平板进行平面度误差评定方法的数据处理采用旋转变换理论，如图1所示。

原始测量数据(格) 每一测点的旋转量 每一测点旋转之后的坐标值

1.1 对角线法评定平面度误差数据处理

对角线法评定平面度误差，是将被测平面上两个对角上的测量点调成等高，以此两点的连线作为基准线。同时调整另外一个对角上的测量点等高，以此两点的连线作为另一条基准线。通过其中一条基准线，且平行另一条基准线的平面作为平面度误差评定的基准平面，所有测点相对于基准平面的最高偏离点与最低偏离点的距离，为被测平面的平面度误差[3]。如式(1)—式(3)。

(1)

(2)

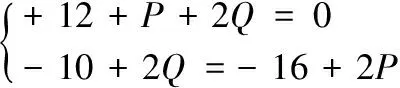
(3)

求得式(1)：P=0.5;Q=-2.5, 求得式(2)：p=-7；Q=-1.5, 求得式(3)：p=-2；Q=-5。

以图1中每一测点旋转之后的坐标值中两个对角旋转到等高为评定原则，列出方程组(1)，求出旋转量P=0.5,Q=-2.5，得到每一测点旋转后的测量值如图2所示。

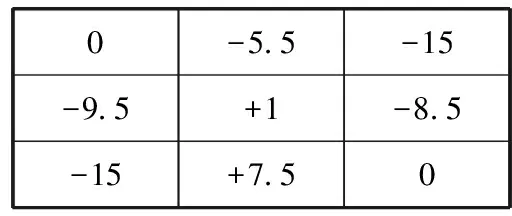
0-9.5-15-5.5+1+7.5-15-8.50

通过其中一条对角线(0—0对角线)，且平行于另一条对角线((-15)—(-15)对角线)的平面为基准平面，实际被测平面上偏离基准平面的最高点为+7.5，偏离基准平面的最低点为(-15)。因此，平面度误差为被测平面的实际测量值的最高点与最低点的差值，即式(4)。

f平面度=(+7.5)-(-15)=22.5

(4)

1.2 三远点法评定平面度误差数据处理

三远点法评定平面度误差，是将被测平面上距离尽可能远的、不在同一直线上的任意三个点调整成等高，以此三点组成的平面作为平面度误差评定的基准平面，所有测点相对于基准平面的最高偏离点与最低偏离点的距离，为被测平面的平面度误差。

以图1中每一测点旋转之后的坐标值中相距尽可能远、且不在同一直线上的三个点旋转到等高为评定原则，列出方程组(2)，求出旋转量P=-7,Q=-1.5，得到每一测点旋转后的测量值如图3所示。

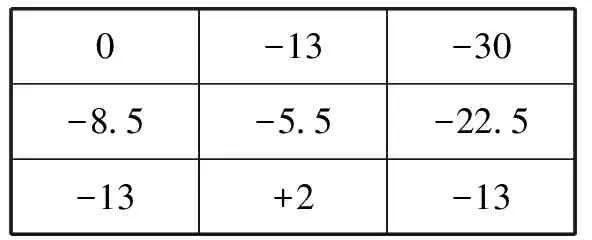
0-8.5-13-13-5.5+2-30-22.5-13

以选中的尽可能相距较远、且不在同一直线上的三个点(-13的三个点)构成一个平面作为基准平面，实际被测平面上偏离基准平面的最高点为+2，偏离基准平面的最低点为(-30)。因此，该平面的平面度误差为式(5)。

f平面度=(+2)-(-30)=32

(5)

1.3 最小区域法评定平面度误差数据处理

最小包容区域法评定平面度误差，是一种最准确、最科学的评定方法。具体要仔细观察所测数据的分布情况，分析所测数据的分布符合最小区域法评定平面度误差的哪一种准则(三角形准则、交叉准则和直线准则)。然后根据被测数据所符合的准则，确定基准平面，所有测点相对于基准平面的最高偏离点与最低偏离点的距离，为被测平面的平面度误差。

仔细观测图1中测量数据的分布情况，发现数据分布符合交叉准则，其中(-10)与(-16)属于两个测量点中的最低点，(+12)与0属于两个测量点中的最高点，且符合两个低点处于两个高点连线的两侧。将图1中每一测点旋转之后的坐标值中两个最高点旋转到等高、两个最低点旋转到等高为评定原则，列出方程组(3)，求出旋转量P=-2,Q=-5，得到每一测点旋转后的测量值如图4所示。

0-8-20-12-4-16-200-10

以通过两个最低点的连线((-20)—(-20)连线)，且平行于两个最高点的连线(0—0连线)的平面为基准平面，实际被测平面上偏离基准平面的最高点为0，偏离基准平面的最低点为(-20)。因此，该平面的平面度误差为式(6)。

f平面度=0-(-20)=20

(6)

1.4 最小二乘法评定平面度误差数据处理

最小二乘法评定平面度误差，需要确定出最小二乘平面。

设(xi，yi，zi)，i=1,2，…,n是直角坐标系中，被测平面上n个测点的坐标值，被测实际平面与最小二乘平面的关系，如图5所示。

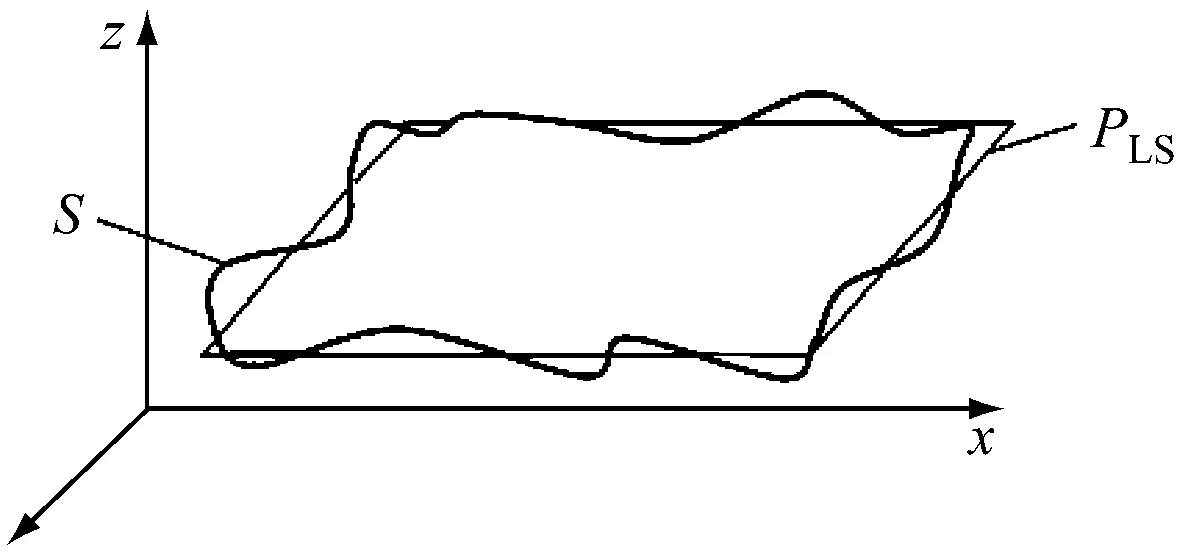
图5 平面度的最小二乘模型

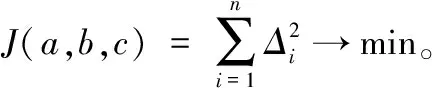
(7)

(8)

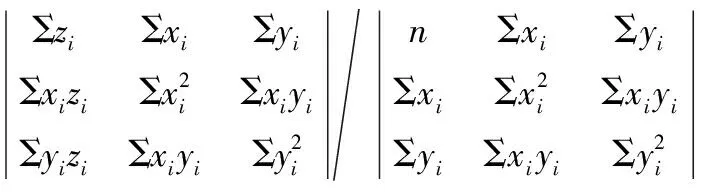
(9)

求出具体的最小二乘平面之后，实际平面上处于最小二乘平面上方的最高点(坐标值为(xM，yM,zM))到最小二乘平面的距离，加上实际平面上处于最小二乘平面下方的最低点(坐标值为(xL，yL，zL))到最小二乘平面的距离之和，为被测平面的平面度误差[5]。为式(10)。

(10)

2 基于MATLAB的平面度误差评定程序设计

2.1 对角线法及三远点法评定平面度误差程序设计

说明：对角线法和三远点法的程序实现区别甚小。以下是对角线法的程序代码[6]，如果采用三远点法进行误差评定，请采用程序中中括号中的代码替换即可。

clear;

clc;

%(数据输入及矩阵行列读入)

X_data=xlsread('三行三列数据3.xlsx'); %read data

X=size(X_data);%

m=X(1,1);

n=X(1,2);

%(制造函数矩阵)

test=zeros(m,n);

X_m=zeros(m,n);

X_n=zeros(m,n);

i=0;

j=0;

for i=0:1:m-1;

X_m(i+1,:)=i;

end

for j=0:1:n-1;

X_n(:,j+1)=j;

end

syms x y;

XM=X_m*x;

XN=X_n*y;

test_1=XM+XN;

%(矩阵合并)

test_2=test_1+vpa(X_data)

%(对角线位置数据采集) 【%(三点位置数据采集)中括号里为三远点法代码】

mm1=1; 【mm1=1;】

nn1=1; 【nn1=2;】

mm2=m; 【mm2=3;】

nn2=n; 【nn2=1;】

mm3=1; 【mm3=3;】

nn3=n; 【nn3=3;】

mm4=m;

nn4=1;

point1=test_2(mm1,nn1) 【point1=test_2(mm1,nn1)】

point2=test_2(mm2,nn2) 【point2=test_2(mm2,nn2)】

point3=test_2(mm3,nn3) 【point3=test_2(mm3,nn3)】

point4=test_2(mm4,nn4)

%(联立方程求解函数) 【%(联立方程求解函数)中括号中为三远点法代码】

form1=point1-point2 【form1=point1-point2】

form2=point3-point4 【form2=point2-point3】

[x,y]=solve(form1==0,form2==0,x,y)

xx=vpa(x)

yy=vpa(y)

%(反代函数矩阵中的最大值和最小值)

Xm=X_m*xx;

Xn=X_n*yy;

test_3=X_m*xx+X_n*yy+X_data

%(求出矩阵中的最大值和最小值)

a=max(max(test_3))

b=min(min(test_3))

%(求出平面度误差)

final=a-b

2.2 对角线法和三远点法评定平面度误差程序运行过程及结果

当被测平面的测量结果为：第一行，0、-18、4；第二行，-6、-2、6；第三行，-24、8、10，采用对角线评定平面度误差，程序运行结果如图6所示。

2.3 最小二乘法评定平面度误差程序设计

%最小二乘法评定平面度误差评定程序[7]

A=xlsread('zxecf.xls');

x=A(:,1);

y=A(:,2);

z=A(:,3);

% n=size(z);

X=[ones(size(z)),x,y];

[b1,bint,r,rint,stats]=regress(z,X); %平面拟合结果，r为误差(点到拟合平面的距离)

a=b1(2);

b=b1(3);

c=b1(1); %平面z=ax+by+c的系数

x0=-20:1:60;

y0=-10:1:30;

[X,Y]=meshgrid(x0,y0);

Z=a*X+b*Y+c;

figure(1)

scatter3(x,y,z,'filled') %绘制散点图

hold on

mesh(X,Y,Z) %绘制拟合平面

[max,index1]=max(r); %距离最大的值及位置

[min,index2]=min(r); %距离最小的值及位置

f0=((z(index1)-z(index2))-a*(x(index1)-x(index2))-b*(y(index1)-y(index2)))/sqrt(1+a^2+b^2); % f0为平面度误差

2.4 最小二乘法评定平面度误差运行结果

最小二乘平面和实际测点分布如图7所示。

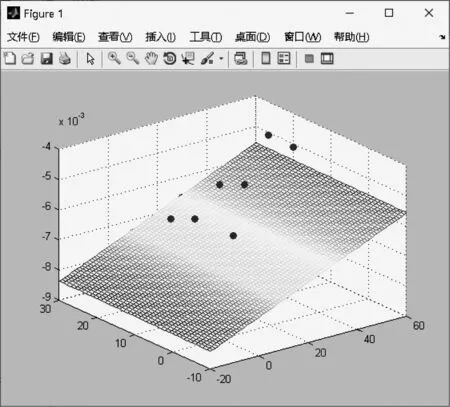
图7 最小二乘平面和实际测点分布图

最小二乘法的运行结果如下。

待定系数：a=3.551 7×10-5；b=8.394 2×10-7；c=-0.007 7。

所有测点到最小二乘平面的最高点距离为：max=0.001 4。

所有测点到最小二乘平面的最低点距离为：min=-0.001 6。

被评定的平面度误差为：f0=0.003 mm=3 μm。

3 程序正确性验证

对于被测平面的测量结果，应用旋转理论，采用对角线评定平面度误差,如图8所示。

图8 对角线法评定平面度误差

手工计算的评定结果[8]为：平面度误差f=35 μm。与计算机程序的运行结果一致。

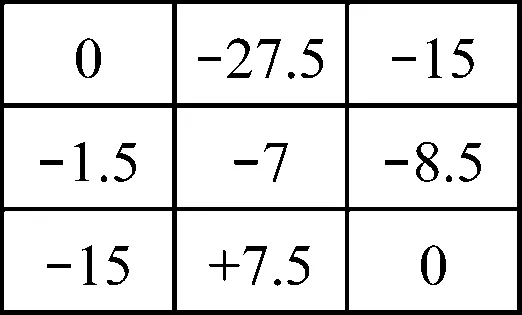
图9 旋转后每一点的测量值

平面度误差为式(11)。

f=+7.5-(-27.5)=35 μm

(11)

通过对多组测量结果，应用旋转理论、采用对角线法、三远点法和最小二乘法评定平面度误差，手工计算或者用EXCEL计算的评定结果，与计算机程序的运行结果一致。

4 总结

对于平面度误差的测量数据处理，采用了程序运行、手工计算和EXCEL计算三种方式进行误差评定，其评定结果相同，验证了程序运行的准确性。可见，应用MATLAB软件对平面度误差进行评定具有结果可靠、便捷、高效等优点值得推广和应用。不仅为其他几何误差评定的程序编写提供了思路和方法，也为数学建模课程的实际应用创造了教学环境，具有实际应用价值和课程改革研究价值。