纳米孔隙中页岩气扩散模拟实验和数学模型分析
2021-11-01王国建朱怀平
邹 雨,王国建,卢 丽,朱怀平,
刘光祥3,袁玉松3,杨海元1,2,金之钧3,4,5
(1.中国石化 油气成藏重点实验室,江苏 无锡 214126; 2.中国石化 石油勘探开发研究院 无锡石油地质研究所,江苏 无锡 214126; 3.中国石化 石油勘探开发研究院,北京 102206; 4.页岩油气富集机理与有效开发国家重点实验室,北京 102206; 5.北京大学 能源研究院,北京 100087)
页岩气藏不同于常规气藏,它是天然气的连续集合体,形成于极低孔低渗、富含有机质的黑色页岩层系中[1]。页岩气赋存状态主要包括裂缝和基质孔隙中的游离气、吸附气和溶解气,产气过程需要气体扩散和解吸,其中甲烷扩散是页岩中重要的气体运移机制,影响着页岩气藏的保存与散失[2-3]。在实际页岩地层中,纳米孔通常为多尺度几何形状,是甲烷从有机质中解吸与在大孔隙或裂缝中流动的中间储集场所和渗流路径,其复杂的孔隙结构特征决定了甲烷的扩散行为[4]。因此,准确、全面地认识多尺度纳米孔隙中页岩气的扩散机制,对储集物性评价、产气量预测、气井布置、配置优化以及高效开发具有重要意义[5-7]。扩散是缓慢的,在浓度梯度驱动下,气体分子可以在各个方向上运移。甲烷在页岩纳米级多孔介质中的扩散行为主要可以分为体相气体扩散和吸附气体表面扩散[6]。在大孔条件下(直径大于10 nm),甲烷分子平均自由程小于孔隙直径,以分子之间的碰撞为主,这种体相扩散被称为Fick扩散;而当孔隙直径小于10 nm时,主要是气体分子在孔壁上的碰撞,是体相扩散的另一种类型,被称为Knudsen扩散[6,8]。吸附气的表面扩散由化学势梯度驱动,对于具有强吸附剂及小孔隙(直径小于2 nm)的基质,表面扩散作用显著,是甲烷在有机物纳米孔中非常重要的传递机制[9]。需要注意的是,在页岩多尺度孔隙条件下,甲烷的各种扩散行为往往是同时进行的,在超临界状态以及不同的温压和岩性条件下存在差异,其机制都需要同时考虑[6-11]。
然而,前人虽然认识到多尺度纳米孔隙、温度、压力及岩性特征等因素对气体扩散系数具有重要影响,但是对页岩纳米孔隙中(直径小于10 nm)甲烷扩散系数的数量级检测(采用游离烃浓度法)结果差异很大,多在10-10~10-5cm2/s之间[7-8,10],且少有涉及高温高压条件和超临界状态,因此有待对这些因素耦合关系进行深入研究。为此,本研究采用常用的游离烃浓度法[12]进行等压扩散模拟实验,对具有多尺度孔隙的页岩样品在高温高压以及不同温压条件下进行原位甲烷扩散实验,从实验模拟分析出发综合探究在不同控制因素影响下的甲烷扩散系数特征,并建立由体相扩散和表面扩散共同组成的数学估算模型。最终,通过实验与理论的相互验证,更真实、全面地描述甲烷在页岩中的扩散行为。
1 模拟实验方案
1.1 实验样品
本次以南方地区寒武系牛蹄塘组中含页岩气层位为研究对象,在鄂西秭归茅坪地区露头剖面进行采样。为了尽可能保证岩样的新鲜和完好,在除去露头风化面后,沿露头垂直向里50 cm采集表面无裂缝、无显著后生变化的黑色页岩样品。前人研究表明[13],鄂西宜昌—秭归地区牛蹄塘组页岩形成于深水陆棚环境,页岩地层连续沉积(最大厚度大于200 m),富含泥晶碳酸盐矿物,具有较高的有机碳含量(TOC约为3.2%),已进入以生气为主的过成熟演化阶段(Ro约为2.5%),为自生气为主的低孔低渗储层。该地区牛蹄塘组页岩气储层顶板为寒武系石牌组致密泥岩,底板为震旦系震旦系灯影组致密硅质白云岩,具有很好的封堵条件,因此页岩中吸附的大量天然气能够很好地保存和富集[13]。
本研究模拟以埋深大于2 000 m和压力大于20 MPa作为深层高压环境。虽然该采样区现今不符合深层条件(周边钻井获得的牛蹄塘组埋深小于1 000 m)[13],但在地质历史时期牛蹄塘组也经历过深层高压(压力甚至大于50 MPa)环境[14],因此本研究在讨论浅层埋深的同时,也将延伸至深层条件下进行理论上的探讨。
按照标准《岩心分析方法:GB/T 29172—2012》[15]对寒武系牛蹄塘组页岩样品进行气体孔隙度测定,结果为1.8 %。采用页岩全孔径分布的测定压汞—吸附联合法对样品孔隙大小及其分布特征进行测试,结果表明页岩孔隙直径中值为2.58 nm,以微孔隙为主(小于2 nm),根据孔径大小,主要可分为4类(图1):直径小于2nm的孔隙占比48%,直径为2~10 nm的孔隙占比9.3%,直径为10~100 nm的孔隙占比15.6%,直径大于100 nm的孔隙占比27.1%。通过扫描电镜(SEM)观测可知(图2),牛蹄塘组页岩为含碳质泥质页岩,结构紧密,发育少量粒间微孔隙,连通性较差。基质内有机质多呈填隙状分布,堵塞绝大部分粒间孔,其中可见极微孔隙(纳米级孔隙)以及少量结构致密的透镜体状有机质。为了进行等压扩散实验,采取平行于页岩样层理面取心,层理面直径为2.5 cm,长度约为0.5 cm;考虑装样和实验过程中岩心需要受力平衡,需要对层理面进行打磨使其平整。

图1 鄂西秭归茅坪地区寒武系牛蹄塘组页岩孔隙直径大小及分布Fig.1 Diameter size and distribution characteristics of shale poresin Cambrian Niutitang Formation, Maoping area, Zigui, western Hubei

图2 鄂西秭归茅坪地区寒武系牛蹄塘组页岩SEM特征Fig.2 SEM characteristics of shale in Cambrian Niutitang Formation, Maoping area, Zigui, western Hubei
1.2 等压扩散实验
为了在原位条件下测试页岩气的扩散系数,本研究团队研制了深层天然气扩散系数模拟实验装置[16],如图3所示,其中A和B扩散室两个高压容器分别与甲烷和氮气源相连。实验过程如下:首先,安装岩心,组装仪器,通过抽真空和试漏的方式验证和保证仪器完全密封,并关闭所有阀门;然后,往A和B室分别充注甲烷和氮气并增压,通过恒温油浴系统控制A和B室温度,该增压过程需要调节环压,保持环压与扩散室之间的压力在10 MPa以内,用来防止压差过大导致岩心破碎(环压相当于模拟地层压力);最后,等待所有实验条件稳定后,使用气密性气体进样针采集A和B室气体,通过Agilent 6980N气相色谱仪检测甲烷气体含量变化。

图3 扩散系数模拟实验装置简易图Fig.3 Simplified diagram of simulatorfor diffusion coefficient analysis
模拟实验过程中,甲烷或氮气在各自的浓度梯度下可从岩心的一端扩散到另一端,甲烷和氮气在高压容器中保持了相同的气体压力,即等压扩散。在这种情况下,岩心的孔隙压力是由扩散室气体压力控制的,通过检测A和B室不同时间段的甲烷气体浓度,可以获得原位条件下的甲烷在页岩中的实验扩散系数。可根据Fick第二定律和物质守恒原理[7],获得扩散系数计算公式(1):
(1)
式中:DF为等压扩散法测得的甲烷扩散系数,cm2/s;C01-C02为两扩散室初始时刻甲烷浓度差,%;Ct1-Ct2为某时刻两个扩散室甲烷浓度差,%;S为薄圆柱形岩心的横截面积,m2;L为薄圆柱形岩心的厚度,m;V1和V2为A和B室体积;t为甲烷扩散时间,s。
为保证DF数值的可靠性及重复性,本研究需保证实验温压条件不变,每隔2~4日对A和B室进行甲烷浓度测试并计算扩散系数,持续一个月以上,要求各时间段获得的DF数值相对标准偏差小于5%。需要注意的是,页岩气在成藏和开发过程中不存在任何双组分扩散系统,该实验其实是模拟真实的分子间碰撞、分子—孔壁碰撞等甲烷扩散行为,来检测理想状态下的扩散系数[8]。本研究以30 ℃、环压8 MPa、气体压力2 MPa为初始实验条件和校准基准,一方面,进行单一气体压力增压(2,10,20,30,45,55 MPa,温度不变)和单一增温(30,50,80,110 ℃,压力不变)模拟;另一方面,同时进行气体压力增压(2~40 MPa)和增温(30~110 ℃)模拟。所有的实验模拟都保持环压和气体压力差值为5~7 MPa。
2 模拟实验结果与讨论
模拟实验测试结果见表1。单一变量实验结果表明,在温度不变的条件下(30 ℃),随着压力增大,扩散系数趋于减小(表1,图4)。该减小的趋势可分为两段,当气体压力小于30 MPa时,扩散系数随压力增大而快速减小;而当气体压力超过30 MPa时,扩散系数减小的趋势变缓,变化趋于平稳。该认识与国内外已发表的研究成果相似,例如,前人以四川盆地下志留统龙马溪组页岩(模拟压力范围为0~20 MPa)[7]、鄂尔多斯盆地上古生界泥岩(模拟压力范围为0~10 MPa)[12]、德国盆地二叠系泥岩(模拟压力范围为0~150 MPa)[17]等为研究对象,通过实验模拟都认为在纳米孔隙介质中,甲烷扩散系数随着压力的增大而减小。不仅如此,计算机分子动力学模拟结果显示,在超深层的高压条件下,甲烷分子处于超临界状态,受限的扩散速度随压力的增大而缓慢减小[18]。

表1 不同温压条件下模拟测试的甲烷扩散系数
在压力不变的条件下(气体压力为2 MPa),随着温度的升高,扩散系数增大,但增大的趋势很缓和(表1,图4)。不同于单一压力模拟实验,温度的升高引起扩散系数呈线性变化。该实验结果同样地与国内外大量研究成果相似,例如前人以四川盆地龙马溪组页岩(模拟温度范围为0~150 ℃)[19]、松辽盆地某盖层岩石(模拟温度范围为0~160 ℃)[20]、德国盆地二叠系泥岩(模拟温度范围为50~200 ℃)[17]等为研究对象,通过实验模拟或理论计算都认为纳米孔隙中甲烷扩散系数与温度呈正相关。这可能是因为气体分子的热运动与温度密切相关,动能随温度的升高而增加,因此总扩散系数有所增大[21]。

图4 扩散系数随单一变量(压力或温度)增加的变化趋势Fig.4 Variation trend of diffusion coefficient with increased single variable (pressure or temperature)
最后,温压耦合模拟实验表明,在温度压力同时增高的条件下,实验扩散系数总体上趋于减小(表1,图5)。温压耦合模拟的是深层页岩气藏的高温高压环境,在这种条件下,天然气组分将处于超临界状态,性质介于液体和气体之间。可见在高温高压环境下,纳米孔隙中的气体压力是影响扩散系数的主控因素,而温度的影响有限。这可能是因为气体压力越大,盖层纳米孔隙单位体积甲烷密度增大,甲烷分子平均自由程减小,气体黏度减小,碰撞次数增大,扩散速度变慢,扩散系数减小[6, 22]。通过以上系统实验得到的只是初步的认识,对于不同的温压条件是如何影响Fick扩散、Knudsen扩散及表面扩散的行为难以通过模拟实验进行分析,有待建立数学模型进行探讨。

图5 温压耦合模拟实验中扩散系数变化趋势Fig.5 Variation trend of diffusion coefficient in simulationexperiment of temperature-pressure coupling
3 数学模型
3.1 体相扩散系数计算
在实际页岩气成藏及开发过程中,虽然发生了吸附气体的表面扩散,但体相和吸附相之间的交换率远远高于表面扩散率[23],其扩散行为如图6a所示。依据Knudsen数(Kn)的大小可将体相扩散划分为Knudsen扩散和Fick扩散:Kn为气体分子平均自由程长度(λ,m)与纳米孔隙直径(D,m)之比,当Kn大于1时,发生Knudsen扩散,而当Kn小于1时,发生Fick扩散[21]。λ与温度和压力都密切相关,温度升高时,λ增大,而压力增大时,λ减小,可通过公式(2)进行计算;而Knudsen和Fick扩散是过渡关系,两者的系数结合(即体相扩散系数)是两者的加权和,可通过公式(3)、(4)和(5)进行计算[6-7, 24-25]:
(2)
(3)
(4)
(5)
式中:κb为Boltzmann常数,取值1.380 5×10-23J/K[7];T为绝对温度,K;δ为气体分子碰撞直径,m;P为气体压力,Pa;Dknudsen为Knudsen扩散系数,Dfick为Fick扩散系数,Dbulk为体相扩散系数,m2/s;r为纳米孔隙半径,m;R为通用气体常数,取值8.314 J/(mol·K)[7];M为气体摩尔质量,kg/mol;μg为气体黏度,Pa·s。因此,结合公式(2)—(5),Dbulk可表示为:
(6)
需要注意的是纳米孔隙在受到应力(即围压与孔隙气体压力之差)的作用下,其半径r会发生压缩形变(图6b),进一步压缩体相扩散的有效性。此时真实的r需要通过以下公式进行计算[10]:
(7)
式中:r0为初始孔隙半径,m;α为Biot系数,无量纲;φ为样品平均孔隙度,无量纲;K为样品体积模量,Pa;Pconfine为施加压力,Pa;εL为Langmuir体积应变常数;PL为Langmuir压力,Pa。
3.2 表面扩散系数计算
在页岩气藏初始条件下,纳米孔表面的吸附甲烷与体相甲烷气体之间存在吸附平衡,吸附甲烷的表面扩散可以利用跳跃模型推导[26]。跳跃模型假设吸附甲烷分子从一个吸附点跳跃到固体表面的相邻吸附点,这是指吸附分子的活化过程。如图6所示,如果被吸附的气体分子能够获得足够的能量跃迁到邻近的吸附位置,则会发生活化和表面扩散。假设纳米孔隙中甲烷分子为单层吸附时,结合跳跃模型理论,利用Langmuir等温线研究页岩气解吸过程更为合理,其中吸附气体浓度可利用公式(8)进行计算[6]:

图6 页岩纳米孔内甲烷扩散过程及机理示意Fig.6 Schematic diagram of methane diffusion process and mechanism in shale nano-pores

(8)
式中:Cs为吸附气体浓度,kg/m3;θ为孔壁表面气体覆盖率,无量纲;NA为阿伏伽德罗常数,6.022 141 5×1023mol-1。尽管Langmuir吸附是单层吸附,但覆盖率θ可定义为吸附体积与Langmuir体积之比:
(9)
于是,在化学势梯度的作用下,吸附气体的表面扩散系数可表示为[6-7]:
(10)
式中:Dsurface为表面扩散系数,m2/s;ΔH为等位吸附热,J/mol;κ为分子阻塞系数(即阻塞速度系数与正向速度系数之比),无量纲;H(1-κ)为Heaviside函数,可表示为:
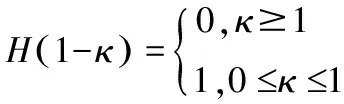
(11)
3.3 总扩散系数计算与矫正
页岩气储层以无数纳米孔为特征,纳米孔被认为是毛细的且弯曲相连的。因此,体相扩散的传输效率还应考虑孔隙度与迂曲度的影响,可通过公式(12)进行评价与计算[27]:
(12)
式中:ζmb为体相扩散矫正系数,τ为迂曲度,无量纲。实际上,还需要考虑纳米孔隙中具有的吸附气体,即真实孔隙大小还受气体分子直径(dM,m)的影响(吸附引起的溶胀响应),如图6所示,孔隙半径r真实有效的半径缩小为r′(r与dM之差)。因此公式(12)应修改为[27]:
(13)
另一方面,表面扩散不仅与ζmb有关,还与吸附层气体横截面积和体相扩散截面积之比有关。于是表面扩散矫正系数ζms可通过公式(14)进行评价与计算[27]:
(14)
需要注意的是,在实际页岩孔隙中,由于不同储层中有机质与页岩基质的体积比不同,表面有机质不连续分布。因此还需要真实表面扩散矫正系数(ζreal-a),该系数是不确定的,ZHONG等[7]建议取值为10-3~10-1。最后,当把矫正后的体相扩散系数与表面扩散系数进行线性相加,则能够得到理论上的总扩散系数:

(15)
总扩散系数公式是理想状态下的,该公式考虑

(16)
4 模型验证


表2 扩散模拟实验和数学模型中的参数取值
试验结果表明,无论ζreal-a和ζreal-b取值如何,公式(16)中的预测结果(Dtotal)的变化趋势都与实验结果一致,即扩散系数表现为随压力增加而减小,随温度升高而增大(图7)。另外,当ζreal-a取值0.001,ζreal-b取值0.005~0.01时,Dtotal在数值上与实验结果(DF)非常接近(图7),这说明该取值在牛蹄塘组页岩样品中具有合理性:(1)ζreal-a取值0.001对应着较小的表面扩散贡献率,这可能是因为牛蹄塘组页岩样品中有机质不连续,而表面扩散多发生在有机质中;(2) 在低压条件下(P<20 MPa),ζreal-b取值0.01时更接近实验结果,而随着压力增高(P>20 MPa),ζreal-b取值0.005时更合理,这可能是因为随着压力增大,孔隙连通性变得更差,导致ζreal-b取值更小。综上所述,对于纳米孔隙页岩气扩散的实验模拟结果(表1,图4和图5),本文中的数学模型可靠,可与其相互验证。

图7 扩散模拟实验与数学模型的相互验证Fig.7 Mutual verification of simulation and mathematical model
5 页岩气扩散理论及应用
在实际的页岩气扩散过程中,不同的影响因素(温度、压力、多尺度孔径、孔隙连通性等)在不同的层位存在变化。于是,基于上述的可靠数学模型,可通过调整不同的影响因素(变量)来深入探讨页岩气扩散行为,结果表明:
(1)总扩散系数随压力的增大而减小,随温度的升高而增大,与模拟实验结果相同。从Fick扩散、Knudsen扩散以及表面扩散作用上看,压力增大虽然能够促使Fick扩散和表面扩散作用加强,但会显著限制Knudsen扩散作用(表3),总体上使得Dtotal减小,并且当压力足够大时(> 30 MPa),扩散系数缓慢减小(图8);然而温度的升高导致分子动能增大,会促进所有的扩散作用(表3),共同使得Dtotal增大(图8)。结合温压耦合特征来看(图9),压力对页岩气扩散作用起主导性作用(相比温度因素),压力的增大导致总扩散作用降低是通过限制Knudsen扩散来实现的,而在纳米孔隙中Fick和表面扩散作用是次要的。

表3 单一变量下的扩散系数特征

图8 纳米孔隙中不同条件下的扩散数学模型Pconfine-P = 5 MPaFig.8 Mathematical model of nano-pores under different conditions

图9 扩散数学模型中温度—压力共同影响下的扩散系数特征Fig.9 Characteristics of diffusion coefficient affectedby temperature and pressure in mathematical model
(2)孔径的增大会显著促进Fick扩散和Knudsen扩散作用,表面扩散作用则被削弱,而其连通性越好越能增强扩散作用(表3,图8)。这可能是因为随着孔径增大,体相扩散的空间更大,因此更多的气体分子会选择耗能较小的体相扩散方式,最终导致Dtotal增大,而孔隙连通性则关系着气体的扩散通道及其行为。对于本文牛蹄塘组页岩样品中多尺度孔径(直径中值为2.58 nm,半径中值为1.29 nm,图1),虽然存在大直径的孔隙(直径大于10 nm,甚至大于100 nm),但由于在高压环境下没有观测到相对应较大的扩散系数,所以这些较大孔隙的连通性可能较差,页岩气扩散还是主要发生在具有微孔隙的有机质中。因此在深层高压环境下,页岩气散失应是以纳米孔隙中的扩散为主。
虽然天然气扩散速度缓慢,但在漫长的地质历史长河中,页岩气扩散造成气藏的散失量通常是可观的[30-31]。因此,基于上文获得的甲烷扩散系数以及前人在上扬子地区地下古生界页岩气研究成果[14, 32-33],可应用于估算牛蹄塘组页岩气藏在地质时期的散失强度,其中散失强度计算公式如下:

式中:QD为页岩气扩散引起的散失量,m3;D为扩散系数,m2/s;t为扩散时间,s;dC/dZ为浓度梯度,m-1;S为扩散散失面积(气藏面积),m2。相比较上文的实验采样区,上扬子地区岑巩区块具有更为完善的成藏史研究与相关成藏地质资料[13,31-33],因此,以岑巩区块牛蹄塘组为计算对象,目前埋深1 200~2 000 m,压力系数为0.91~1.13,平均厚度60 m,甲烷含量平均79.6%[32],结合其成藏热演化史可知其在地质历史时期所受压力约在11~50 MPa,在印支运动之前牛蹄塘组以沉降为主(约400~250 Ma),之后印支运动至今以抬升为主(约250~0 Ma)。考虑压力、温度及孔隙特征,将数据代入本文数学模型可粗略计算得到牛蹄塘组天然气在纳米孔隙中的扩散系数约在(0.02~4)×10-7cm2/s范围内,其中印支运动之前的扩散系数均值约为8×10-9cm2/s,在此之后的扩散系数均值约为4.9×10-8cm2/s。将扩散系数代入公式(17)可得沉积时期牛蹄塘组页岩气累积散失强度仅为0.5×108m3/km2,而抬升时期累积散失强度为5.1×108m3/km2,即在地层抬升释放压力的过程不利于气藏保存,该过程是页岩纳米孔中天然气散失的主要阶段。且相比于上扬子地区川东北和川东累积供烃能力(分别为60.59×108m3/km2和14.32×108m3/km2)[33],总的累积扩散量不容忽视。
6 结论
(1)以鄂西牛蹄塘组页岩为研究对象,考虑并量化了温压条件,页岩纳米孔特征(孔径、孔隙率、弯曲度、压缩变形等),以及岩性特征等因素对体相扩散(Fick、Knudsen扩散)和表面扩散的影响,实现了模拟实验与数学模型的相互验证,证明了甲烷扩散理论分析的可靠性。模拟实验结果表明,在温度不变的条件下,总扩散系数随压力的增大而减小,而当压力增至30 MPa以上,系数趋于稳定;在压力不变的条件下,总扩散系数随温度升高而增大;而在温压同时增高的情况下,总扩散系数趋于减小。
(2)数学模型计算结果表明,温度的升高会促进体相和表面扩散作用,这是因为高温能增加分子动能;压力的增大会使得Fick扩散和表面扩散加强,但会显著抑制Knudsen扩散作用,使得总扩散系数减小;而孔隙的增大会显著加强体相扩散作用,稍微限制表面扩散的贡献,最终是使得总扩散系数增大;在深层高温高压环境下,压力是控制页岩气扩散行为的主要因素,通过计算表明岑巩区块牛蹄塘组在沉降过程中气藏累积散失强度较小,显著小于其在地层抬升释放压力过程中的散失强度。
