土石混合体地层中基坑开挖对邻近既有隧道影响

杨 波，谭 勇

(1.同济大学 地下建筑与工程系，上海 200092； 2.岩土及地下工程教育部重点实验室(同济大学)，上海 200092)

随着中国城市建设的加速，城市地下轨道交通网络日益密集。同时，国内各地的土地开发作业不断地向地下寻求空间，导致城市范围内深基坑工程不断涌现。因此，城市地铁隧道在其使用期限内不可避免会受到邻近深基坑开挖卸荷作用的影响[1-2]。近年来，在中国东北部及中西部的城市建设过程中频繁遭遇到土石混合体这一特殊地质条件[3-4]，与常见均质土体不同，其特有的微观结构导致该种地质材料的物理力学性质具有离散性和复杂性[5]，其材料变形破坏机制也受到微观结构与组成粒度的影响[6]。因此，土石混合体中基坑开挖卸荷引起的邻近地层响应及其中的隧道结构响应机制较一般均质土体中更为复杂。考虑到城市环境保护及地铁隧道安全等问题，针对土石混合体地层中基坑开挖对邻近既有隧道的影响研究具有现实意义及工程意义。

迄今为止，国内外学者针对基坑开挖对邻近既有隧道的影响这一问题进行了丰富的研究，随着近年来计算机计算能力和软件技术的发展，较多研究采用数值模拟手段，对地层中的基坑围护结构及隧道结构进行数值建模，并计算模拟施工过程。郑刚等[7]采用有限元分析软件ABAQUS，基于理想弹塑性Mohr-Coulomb模型分别从二维、三维角度分析了软土地层中基坑开挖对开挖面下卧隧道结构及土体的作用机理；蔡建鹏等[8]基于基坑变形统计预测曲线，提出了基于位移控制有限元法(DCFEM)，并就基坑开挖对邻近地下管线的变形及内力影响进行分析；Huang等[9]采用土体硬化模型(harding soil model)，基于有限元理论分析了基坑开挖卸荷引起的隧道三维变形响应，得到了开挖引起的下卧隧道结构响应影响范围结果；戴鹏祥等[10]采用能够考虑土体小应变特性的亚塑性模型，基于有限元计算方法对已有离心试验模型进行了三维数值模拟，结果表明亚塑性本构模型对于该问题的研究具有较好的适用性；宋晓凤等[11]基于北京某地铁区间隧道旁基坑工程实例，运用有限单元法进行数值分析，对粉质黏土地层中基坑开挖对邻近地铁盾构隧道结构及轨道结构的影响进行了分析。上述针对开挖卸荷对邻近既有隧道的影响研究无一不限于黏土、粉土、砂土等细粒土均质地层，而针对非均质的、各向异性的粗粒土地层中同一工程问题的研究仍十分少见。

同时，已有较多研究采用数值模拟手段对土石混合体的物理力学特性进行了详细的研究。考虑到土石混合体材料本身具有较强的不连续力学特性，多数研究以离散单元法为基础。徐文杰等[12]基于三维离散元软件YADE，以球体单元模拟土石混合体中不同粒径单元，并分别研究了含石率、试样尺寸、强度参数对土石混合体力学性质的影响；薛亚东等[13]基于PFC2D颗粒流离散元软件，采用二维圆盘单元模拟土石混合体试样并进行了数值剪切试验，分析了含石率与剪切变形和材料强度间的关系；Ricardo等[14]基于球体单元建立土石混合体的数值模型，并研究了含石率对土石混合体力学性能的影响，发现土石混合体的抗剪强度在含石率等于75%时达到峰值；赵金凤等[15]基于非规则组合颗粒建立土石混合体数值模型，并研究了含石率与土石混合体力学性能间的相关关系；Ng等[16]基于椭球颗粒单元建模就颗粒形状及粗颗粒含量对混合体力学特性的敏感性进行了研究，发现土石混合体的峰值抗剪强度受颗粒形状的影响更为显著。 上述研究仅针对土石混合体作为地质材料的物理、力学特性进行了探讨，以含石率、石块粒径、孔隙率等参数对混合体力学性能的影响为研究重点，而针对土石混合体复杂地层中具体工程问题的研究仍较少见。

基于以上综述，前期针对土石混合体地层中基坑开挖对邻近既有隧道的影响问题进行了室内模型试验研究[17]。由于试验操作难度大、时间周期长等限制，前期试验仅就一种隧道位置条件下含石率对开挖引起的隧道结构响应影响进行了定性化探究。另外，由于测量设备的限制，室内模型试验难以对不同含石率条件下土石混合体地层中开挖引起的地层与管片作用机理进行探究。因此，有必要采用数值模拟手段对不同隧道位置条件下，不同含石率时基坑开挖引起的隧道结构响应规律进行深入的机理性探究。

本文采用数值模拟手段，基于平面应变假设，采用PFC2D颗粒流计算软件对土石混合体地层及基坑围护结构、隧道结构进行精细化数值建模，对不同含石率w(%)下土石混合体地层中基坑开挖引起的隧道内力及变形响应进行了研究。

1 数值模拟模型

1.1 土石混合体模型

1.1.1 细粒土参数标定

PFC2D通过设定颗粒单元间的微观接触参数来描述整体材料的力学行为，因此，难以将土体宏观参数与颗粒微观参数进行直接的参数转换。需先进行数值双轴试验，通过与前期室内直剪试验[17]得到的砂土力学性质参数进行对比对土体颗粒的模拟参数进行确定。

由于计算机计算能力的限制，在PFC2D中往往以一定粒径比例放大后的圆盘单元(disk)模拟细粒砂土，根据已有研究[18]提出的合理尺寸效应比，选取砂土圆盘颗粒的直径为1～2 cm，孔隙比e为0.18，天然密度ρ为1 800 kg/m3。砂土颗粒接触模型采用线性接触模型(Linear)，接触参数如表1所示。

表1 砂土颗粒接触模型参数

图1、2分别为数值双轴试验得到的应力-应变曲线及相应的摩尔圆。数值试验得到的试样内摩擦角φN=33.3°，前期室内直剪试验[17]得到的砂土内摩擦角φE=32.78°，二者吻合程度较高。

图1 砂土双轴试验应力-应变曲线

图2 数值双轴实验摩尔应力圆

1.1.2 土石混合体模型

多数研究[12-13]采用Clump颗粒簇单元模拟土石混合体中的块石等粗颗粒体。然而，简单的Clump单元难以精确模拟块石颗粒带有棱角的形状特征，且直接在PFC2D中难以快速生成较多不同几何形状的粗颗粒体模型。本文采用的方法可根据土石混合体中粗颗粒体的含量、粒径范围、棱角数、孔隙比等参数，快速生成带棱角的随机形状的粗颗粒体模型，具体生成方法见文献[19]。将1.1.1节中标定过的砂土颗粒按照含石率填充至块石颗粒间隙中，从而实现土石混合体的精细化建模。图3为PFC2D中土石混合体细观结构示意。块石颗粒同样采用线性接触模型(Linear)，接触参数如表2所示。考虑到模型计算效率，最终选取的块石粒径为20～40 cm。

表2 块石颗粒接触模型参数

图3 土石混合体结构示意

1.2 隧道模型

研究的隧道结构管片外径D=6.0 m，管片壁厚t=0.3 m，管片材料采用C50钢筋混凝土，密度ρ=2 500 kg/m3，弹性模量E=3.5×104MPa，泊松比υ=0.35。采取一簇沿圆环排列的圆盘颗粒(disk)，以及颗粒间平行粘结接触模型(linear parallel bond)实现隧道管片结构的模拟。

研究前需对隧道管片的受力变形性能进行标定。通过对隧道拱顶、拱底施加竖向集中荷载和均布荷载，并对隧道拱顶变形δ1及腰部变形δ2的数值计算结果和按结构力学计算的理论结果进行对比，实现隧道结构的标定。隧道管片颗粒微观参数选取如表3所示。隧道管片的受力变形标定结果如表4所示。需要说明的是，表4理论值计算过程中，考虑到隧道管片的接缝作用，对管片刚度进行了折减。现有研究表明[20-21]，隧道管片接缝导致的横向刚度折减系数η取值范围为0.4～0.8，本文中折减系数η取0.7。

表4 隧道管片标定结果

1.3 基坑围护结构模型

基坑围护结构采用“地下连续墙+钢支撑”的结构形式，开挖深度16.0 m，开挖宽度30.0 m，内设四道钢支撑。参考DG/TJ08-61—2010基坑工程技术规范相关内容，对基坑围护结构参数进行选取。地下连续墙深30 m，厚0.8 m。钢支撑长30 m，支撑截面尺寸φ609@16。基坑分5步开挖，每步分别开挖至地表下1.5、5.5、9.5、13.0、16.0 m深度。

1.3.1 地下连续墙标定

地下连续墙采用4列规则紧密排列的圆盘颗粒(disk)模拟，颗粒直径0.2 m。颗粒参数如表5所示。地下连续墙截面宽度为单位长度1 m，厚度0.8 m。

表5 基坑围护结构颗粒参数

地下连续墙采用悬臂梁自由端点受横向集中荷载作用下的端点横向变形为指标，通过对数值计算结果及理论计算结果的对比，对地下连续墙的横向变形性能进行标定。由于本文并不对结构的破坏进行研究，且平行粘结模型属于弹性本构范畴，出于计算效率考虑，标定中采用了较小的荷载值。标定结果如表6所示。

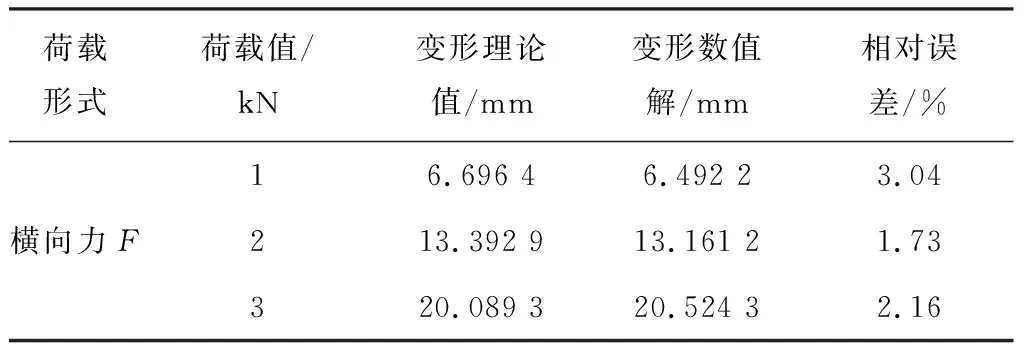
表6 地下连续墙横向变形性能标定结果

1.3.2 钢支撑标定

钢支撑采用一排规则紧密排列的圆盘颗粒(disk)模拟，颗粒直径0.2 m。颗粒参数如表5所示。钢支撑截面尺寸为φ609@16，截面积为0.030 6 m2。

钢支撑采用悬臂梁自由端点受轴向集中荷载作用下的端点轴向变形为指标，通过对数值计算结果及理论计算结果的对比，对钢支撑的轴向变形性能进行标定。标定结果如表7所示。

表7 地下连续墙轴向变形性能标定结果

1.4 数值模拟模型及验证

1.4.1 数值模拟模型

针对隧道位于基坑开挖后主动土压力区及被动土压力区两种工况下，不同含石率w(%)对开挖卸荷引起的隧道结构响应影响进行研究。所采用的计算模型示意如图4所示。

图4 数值计算模型示意(m)

在PFC2D软件中实现既有隧道结构旁基坑开挖施工全过程的具体流程如下：

1)采用刚性墙体Wall单元建立模型边界；

2)采用Ball单元及Clump单元在模型边界内进行填充，使其在自重作用下填充密实，模拟土石混合体地层并达到地应力平衡；

3)删除隧道截面区域内的土体颗粒，并生成以标定好参数的平行粘结模型粘结起的一簇圆环状排列的Ball颗粒，计算至系统平衡，模拟隧道的开挖施工；

4)删除地下连续墙槽内的土体颗粒，并在槽中生成以标定好参数的平行粘结模型粘结起的一系列矩形排列的Ball颗粒，计算至系统平衡，模拟地下连续墙的施工；

5)删除各步开挖区域范围内的土体颗粒，计算至系统平衡或地层位移停止发展，随后在拟定深度处生成一横条排列的以平行粘结模型粘结的Ball颗粒作为支撑，模拟各步开挖施工；

6)循环第5)步操作直至开挖至基坑底面。

1.4.2 与模型试验对比验证

室内试验设置了如图4(a)模型箱布置的数值模拟对照试验组，在纯砂土条件下(w=0)进行了参数d=1、5、10 m 3组工况试验。采用本文数值模拟方法在PFC2D中进行了相同的对照组数值试验模拟。考虑前期室内模型试验是针对定性规律研究的非相似性试验，若要将模型试验结果与定量化数值模拟结果进行对比以验证数值模拟方法的合理性，需要将对比指标进行无量纲化，以反映该指标受开挖引起的变化趋势规律。因此，将室内试验与数值模拟得到的不同d参数下隧道管片受开挖引起的变形无量纲化结果进行对比，结果如图5所示。纵坐标δD指每一步工序下的隧道内径变形量，δDmax指施工全过程中隧道内径最大变形量。可以看出，二者吻合较好，从而对本文采用的基坑及隧道开挖数值模拟方法进行了验证。

图5 数值计算模型与模型试验对比验证结果

1.4.3 与实际工程对比验证

通过对某土石混合体地层中地铁车站基坑工程[22]的开挖施工全过程进行数值模拟，采用PFC2D软件及本章所述的模型建立方法，将数值模拟计算得到的围护墙水平位移结果与现场实测结果进行对比，从而对本文土石混合体中开挖数值模拟方法的合理性进行验证。对比结果如图6所示。随着支撑的逐步施加，数值模拟支撑与实际支撑刚度间的误差导致第3步、第4步开挖时数值模拟最大变形位置较实际最大变形位置有所下移，但位置误差在3 m以内，且最大变形量较为接近，证明数值模拟方法具有较好的合理性。

图6 数值计算模型与实际工程对比验证结果

2 主动土压力区隧道模型结果

对隧道位于开挖主动土压力区时工况(如图4(a))进行隧道开挖及邻近基坑开挖全过程的模拟计算。隧道与基坑围护结构间水平净距d=5 m，隧道圆环圆心与基坑底面深度齐平。本章将对此工况下不同地层含石率w对开挖引起的隧道结构响应影响进行分析。

2.1 基坑开挖变形

图7为开挖引起的地下连续墙最大横向变形与地层含石率w的关系。可以看出，当w≤60%时，地下连续墙最大横向变形与含石率w近乎呈线性增长关系；当w>60%时，地下连续墙最大横向变形随含石率增长呈快速下跌趋势。

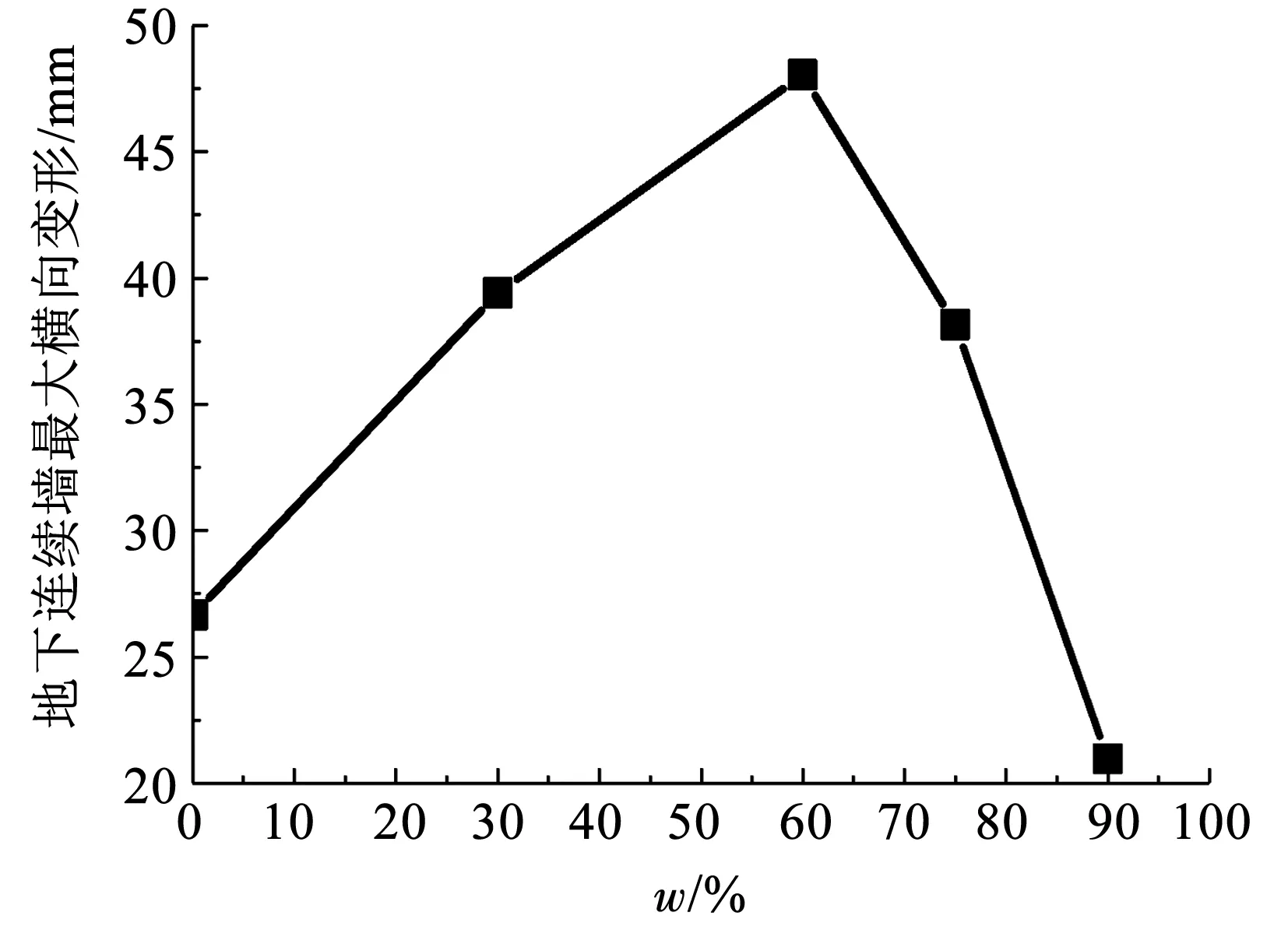
图7 地下连续墙最大横向变形与含石率w关系

图8为开挖引起的最大坑外地表沉降与地层含石率w的关系。可以看出，当w≤60%时，最大地表沉降与含石率w大致呈线性增长关系，当w>60%时，最大地表沉降随地层含石率w的增长大幅度线性下跌。

图8 最大坑外地表沉降与含石率w关系

2.2 隧道管片内力

图9为不同含石率w条件下开挖引起的隧道管片横向弯矩。可以看出，当w=0时，隧道弯矩始终呈现“∞”形分布，当含石率w增大至60%时，管片弯矩分布形状产生了90°的偏转，当w达75%及90%时，隧道管片横向弯矩的分布呈现复杂性和多样性。

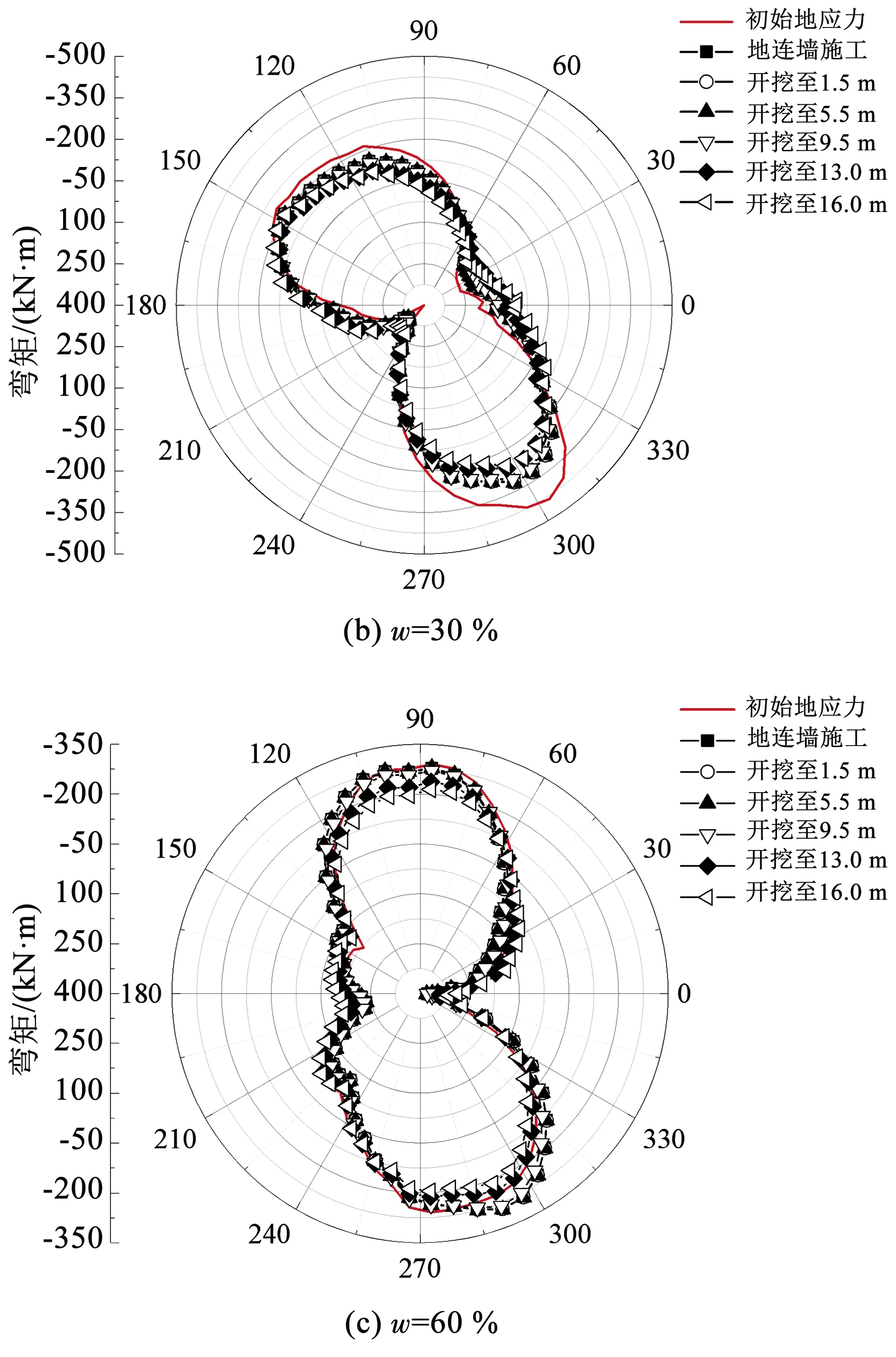
图9 不同含石率w下隧道管片弯矩

图10为开挖引起的最大弯矩增量与含石率w的关系。从变化量大小来看，当w≤60%时，开挖引起的最大弯矩变化值随地层含石率w的增加而呈线性上升；当w>60%时，开挖引起的最大弯矩变化值随地层含石率w的增加呈线性减小。

图10 最大弯矩增量与含石率w的关系

2.3 隧道管片变形

2.3.1 管片内径变形

考虑到不同含石率工况下初始地应力条件不同，隧道管片初始内径变形不同，对仅由开挖引起的内径变形增量进行分析。图11为不同含石率w下开挖引起的隧道水平内径、竖直内径增量。可以看出，当w≤60%时，内径变形增量随地层含石率w的增加而上升；当w>60%时，内径变形增量随地层含石率w的增加而下降。当w=90%时，隧道内径增量的发展规律与其余含石率工况不同，造成该现象的原因可在2.4节中进行解释。总体上，隧道管片内径增量在w=60%时达最大值，在w=90%时达最小值。

图11 不同含石率w下隧道管片内径变形增量

2.3.2 管片刚体位移

图12为不同含石率工况下隧道刚体位移。可以看出，整体上隧道以朝向开挖法向主要产生水平位移，且当w≤60%时，隧道水平位移随地层含石率w的增加而上升；当w>60%时，隧道水平位移随地层含石率w的增加而下降。当w=60%时，隧道水平位移达到最大值。

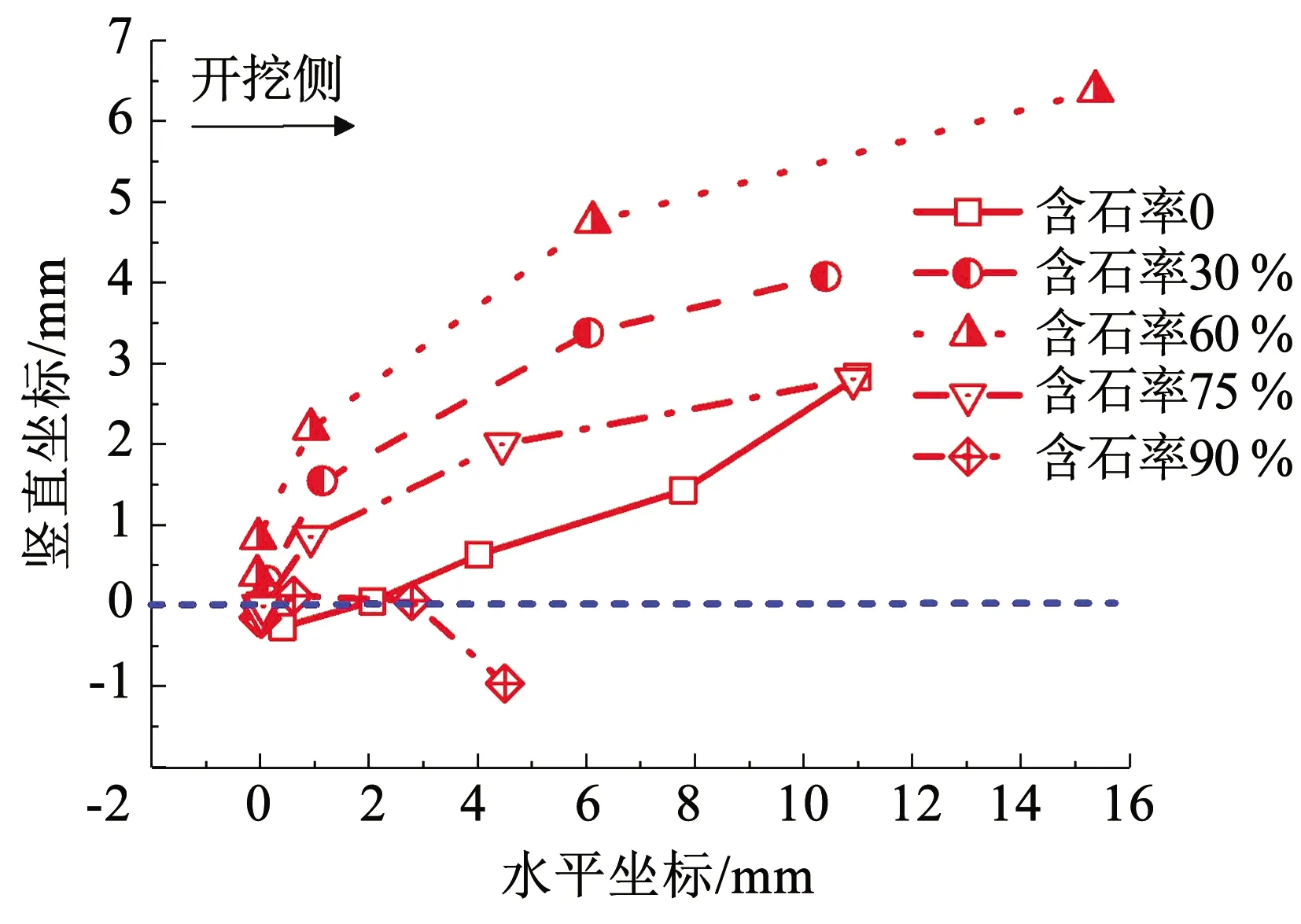
图12 不同含石率w下隧道刚体位移

2.4 隧道管-土接触力

为了清晰地观察并分析不同含石率下的地层微观结构及接触力链，对如图13标示位置处的地层颗粒及颗粒间接触力链进行放大，局部区域放大后的地层颗粒及接触力链如图14所示。

图13 地层颗粒及接触力链局部放大位置示意

图14中，黄色大圆颗粒为隧道衬砌，灰色小圆颗粒为细粒土，黑色颗粒为块石，红色矩形条为颗粒间接触力单元，其宽度代表了接触力大小水平。可以看出，当w=0时，接触力链表现出典型的连续介质特征，力链较为完整且连续。当w≤60%且不断增长时，力链逐渐变得不连续，说明土石混合体地层的松散性逐渐增强。当w>60%且不断增长时，力链分布逐渐变得离散，尤其当w=90%时，地层中形成了以块石间点对点接触为组成单元的连续块石骨架体。因此，w=60%是土石混合体地层由松散体向块石骨架体转变的节点。

图14 不同含石率w下局部位置地层颗粒及接触力链

图15为不同含石率工况下开挖引起的隧道周围管-土接触力变化。可以看出，当w=0时，隧道管片接触力主要在0°～60°位置处发生明显减小，且在以隧道圆心为对称中心的对称位置处有明显接触力增大现象。当w=30%、60%时，隧道管片主要在右侧出现了明显的接触力减小现象，且接触力的减小量随w的增加而增大，在w=60%时达到最大值。当w=75%、90%时，隧道周围接触力总体上减小，但减小的位置分布较零散。上述现象说明，当w≤60%时，含石率的增长导致土石混合体地层的松散体特性增强，地层抗剪强度下降；当w>60%时，含石率的增长导致地层中逐渐形成较完整的块石骨架体，土石混合体地层抗剪性能增强。因此，当w=60%时，隧道侧边开挖引起的地层变形、隧道内力、变形响应均达到峰值水平。

图15 不同含石率w下隧道管-土接触力增量

3 被动土压力区隧道模型结果

对隧道位于开挖被动土压力区时工况(如图4(b))进行隧道开挖及邻近基坑开挖全过程的模拟计算。隧道与基坑开挖底面竖直净距h=5 m。本章将对此工况下不同地层含石率w对开挖引起的隧道结构响应影响进行分析。

3.1 基坑开挖变形

图16为开挖引起的地下连续墙最大横向变形与地层含石率w的关系。可以看出，地下连续墙变形规律与2.1节中类似，当w≤60%时，地下连续墙最大横向变形与含石率w近乎呈线性增长关系；当w>60%时，地下连续墙最大横向变形随含石率增长呈快速下跌趋势。

图16 地下连续墙最大横向变形与含石率w关系

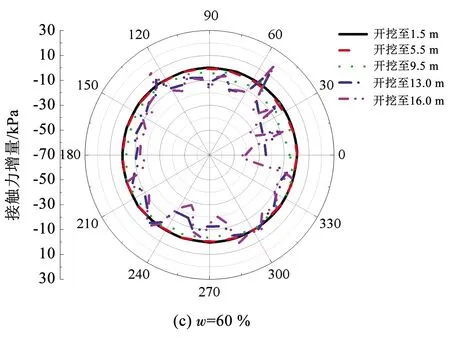
图17为开挖引起的最大坑底隆起与地层含石率w的关系。可以看出，当w≤60%时，最大坑底隆起随含石率w增长而略微增大，当w>60%时，最大坑底隆起随地层含石率w的增长大幅度下跌。

图17 最大坑底隆起与含石率w关系

3.2 隧道管片内力

图18为不同含石率w下开挖引起的隧道管片横向弯矩。可以看出，当w=0时，隧道弯矩大体呈现“∞”形分布；当w达30%、60%、75%时，弯矩分布呈现“8”字形分布；当w=90%时，弯矩分布呈现复杂性。

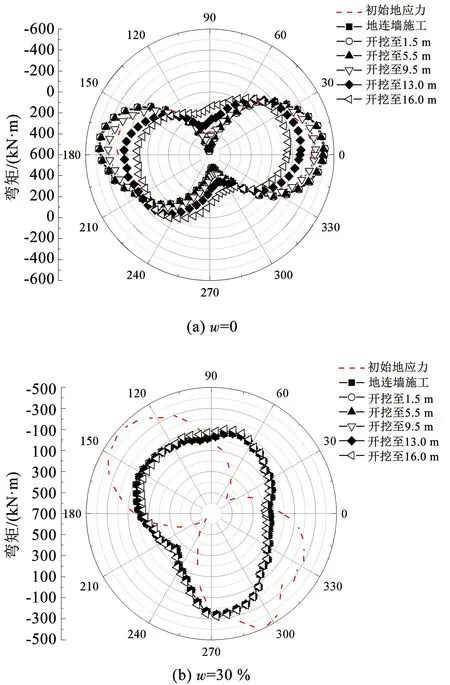
图18 不同含石率w下隧道管片弯矩

图19为开挖引起的最大弯矩增量与含石率w的关系。可以看出，当w=0时，隧道弯矩最大变化量约398.6 kN·m，当w=30%、60%及75%时，隧道弯矩最大变化量较为相近，且远小于w=0情况。其原因主要是含石率的增长导致土体重度增大，从而对隧道上方卸荷作用起到抑制。当w=90%时，最大弯矩变化量出现回升现象。

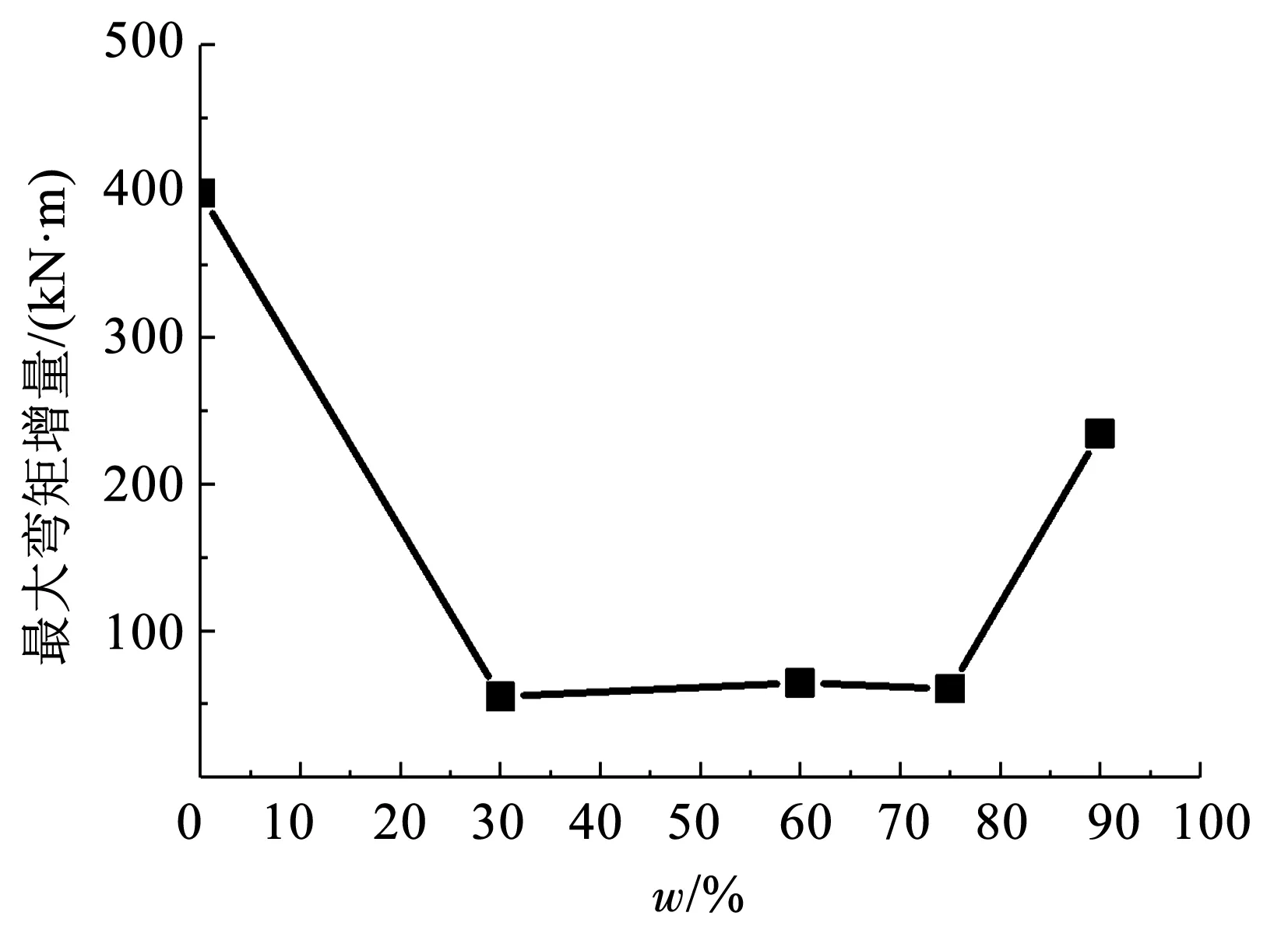
图19 最大弯矩增量与含石率w的关系

3.3 隧道管片变形

3.3.1 管片内径变形

与2.3.1节的分析方法相同，对仅由开挖引起的内径变形增量进行分析。图20为不同含石率w下开挖引起的隧道水平内径、竖直内径增量。可以看出，当w=30%、60%、75%时，收敛变形变化量较为相近，且远小于w=0情况。而当w=90%时，开挖引起的收敛变形变化量有明显回升，其值介于w=0及75%两种情况。

图20 不同含石率w下隧道管片内径变形增量

3.3.2 管片刚体位移

图21为不同含石率工况下隧道刚体位移。可以看出，w=0时隧道产生的竖向位移占主要地位，远超过其余各地层含石率工况，w=90%条件下产生的竖向位移其次。当w=30%、60%、75%时，隧道受开挖引起的竖向位移及水平位移均相对不明显。

图21 不同含石率w下隧道刚体位移

3.4 隧道管-土接触力

为了清晰地观察并分析不同含石率下的地层微观结构，对如图22标示位置处的地层颗粒及颗粒间接触力链进行放大，局部放大后的地层颗粒及接触力链如图23所示。

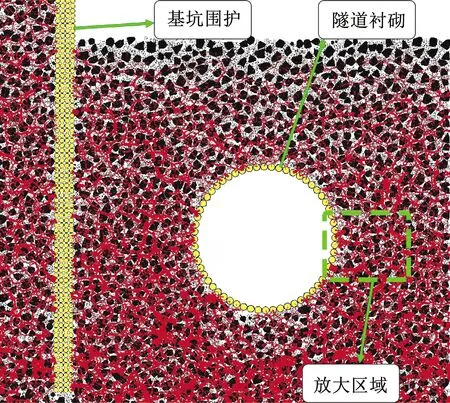
图22 地层颗粒及接触力链局部放大位置示意

图23中黄色大圆颗粒为隧道衬砌及基坑围护结构，灰色小圆颗粒为细粒土，黑色颗粒为块石，红色矩形条为颗粒间接触力单元，其宽度代表了接触力大小水平。可以看出，与2.4节中结果较为相似，当w≤60%且不断增长时，块石含量的增长逐渐降低了地层介质的连续性，且块石间未形成直接接触，地层松散程度上升。当w>60%且不断增长时，块石间逐渐形成连续的接触链，当w达90%时，地层大体上形成了以块石骨架为主体，以细颗粒为填充的微观结构。

图23 不同含石率w下局部位置地层颗粒及接触力链

图24为不同含石率工况下开挖引起的隧道周围管-土接触力变化。可以看出，当w=0时，隧道主要在顶端附近及底端附近产生了较明显的土压力减小。当w=30%、60%、75%时，隧道周围土压力的减小量明显小于w=0工况，证明在含石率较高的松散体地层中，由于隧道上覆土重度的增大，隧道正上方的卸荷作用对管-土接触力的影响较不明显。当w=90%时， 隧道周围土压力变化大小介于前面两种情况，且主要在隧道顶端及底端产生较明显的接触力减小。此现象说明竖向的卸荷作用引起了块石骨架体的松脱，导致深层块石接触力链的断裂和重塑。上述隧道周围管-土接触力分布变化规律对本节所分析的由开挖引起的隧道内力、变形规律进行了解释。

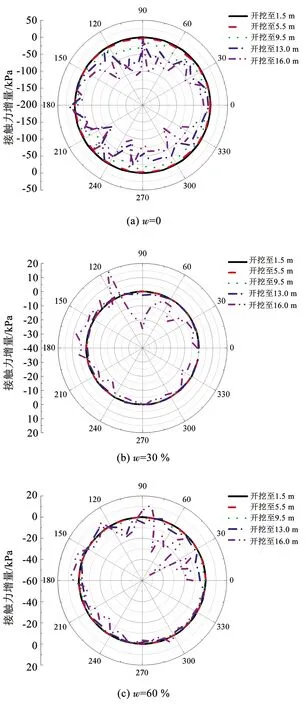
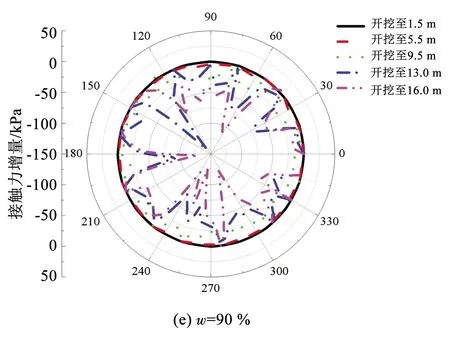
图24 不同含石率w下隧道管-土接触力增量

4 结 论

1)开挖引起的变形包括坑外地表沉降、坑底隆起、围护结构横向变形在w=60%时达到最大峰值。

2)隧道管片横向弯矩分布随含石率变化而呈现多样的分布形态。隧道位于主动土压力区时，开挖引起的弯矩变化在地层含石率w=60%时达到峰值。隧道位于被动土压力区时，开挖引起的弯矩变化在w=0时最大，且与w=90%时相近，当w=30%、60%及75%时内力的变化较为接近且最小。

3)隧道位于基坑开挖主动土压力区时，开挖引起的内径变化、隧道位移在地层含石率w=60%时达到峰值；隧道位于基坑开挖被动土压力区时，开挖引起的内径变化、隧道位移在w=0时最大，当w=30%、60%及75%时内径变化远小于w=0情况，当w=90%时内径变化介于前两种情况。

4)隧道位于主动土压力区时，开挖引起的隧道右侧土压力下降幅度在w=60%时达到最大值；隧道位于被动土压力区时，当w≤75%时，含石率的提升导致隧道上方覆盖的松散土体重度增加，从而引起隧道周围土压力下降幅度整体减小。当w=90%时，隧道上方开挖引起块石骨架松脱，导致隧道圆环顶端及底端土压力产生大幅下降。

5)隧道位于主动土压力区时，仅当基数大于60%时的地层含石率提升对侧边开挖引起的隧道内力、变形响应具有抑制作用；隧道位于被动土压力区时，基数不高于75%时的地层含石率提升对上方开挖引起的隧道响应具有抑制作用，而当地层中已形成块石骨架体时(含石率达到90%)，地层含石率的提升无法为开挖引起的隧道内力、变形响应提供抑制效果。