带有扰动的变时滞离散系统可达集估计

庄 苏，丛玉豪,2

（1. 上海大学 理学院，上海 200444；2. 上海海关学院，上海 201204）

可达集估计是控制理论中一个重要的研究课题，它在许多领域有着广泛的应用，如安全检查[1]、峰间极小化[2]、参数估计[3]和具有饱和执行器的控制系统[4]。系统的可达集是指从初始条件出发，能够到达的所有系统状态的集合。通常人们很难获得可达集的精确特征，所以，需要确定一个能够界定可达集的区域，并且希望这个区域能够尽可能的小，这就是可达集估计问题。

众所周知，在工程和实际系统中，一方面，由于数据变换、测量误差、线性化近似等原因，扰动输入现象是不可避免的。对于具有有界峰值扰动的系统，研究可达集估计问题的最新方法之一就是椭球体技术，其目的是确定包含可达集的椭球体。Boyd等[1]提出，这种椭球可以通过使用Lyapunov方法和线性矩阵不等式（LMI）技术获得。

另一方面，在各种实际系统中，时滞经常发生，它的存在可能导致系统不稳定[5]。然而目前对于时滞系统可达集的研究还比较少。因此，如何找到一个尽可能小的估计来界定时滞系统的可达集引起了许多学者的关注[6-12]。Fridman等[6]采用Lyapunov-Razumikhin方法研究了带有有界峰值扰动的时变时滞连续线性系统的可达集估计问题；Kim[7]改进了Fridman等的研究成果，通过建立适当的Lyapunov-Krasovskii泛函，提出了一个改进的可达集椭球界，其中时滞相关条件以仅涉及一个非凸参数的矩阵不等式形式给出；Zuo等[8]提出了一种用于多面体不确定系统可达集估计的极大Lyapunov-Krasovskii泛函方法；Nam等[9]认为时滞下限不必为零，提出利用时滞分解技术来估计可达集。

值得注意的是，上述文献中考虑的系统都是连续的。实际上，随着计算机技术的发展，大多数控制工程应用系统都是数字实现的。因此，直接对离散模型进行研究更为合理。到目前为止，对于离散时滞系统的可达集估计问题的研究还很少。That等[10]讨论了受状态时滞和有界扰动的线性离散系统的可达集有界问题，提出了一种新的极轴投影的概念；Lam等[11]研究了具有有界扰动和多重常时滞的离散多面体系统的可达集估计问题。但是上述结果仅仅针对开环系统，而对于系统可达集估计的控制器设计问题研究成果较少。比如，Zhang等[12]研究了具有分布时滞的连续系统的控制器设计问题；Chen等[13]研究了离散线性切换系统的状态反馈控制器设计问题，但并未考虑时滞对系统可达集估计的影响。但有关利用反馈控制器来研究离散变时滞系统的可达集估计问题还未被涉及。此外，上述文献都假设系统的初始值为零，这个条件在可达集估计的过程中带来了一些限制。

本文在有界扰动下，研究了一类变时滞离散系统的可达集估计和控制器设计问题，其中系统的初始值不再要求为零。利用Lyapunov-Krasovskii泛函方法，得到界定闭环系统可达集的充分条件。之后，通过求解优化问题，确定了一个尽可能小的区域来估计系统的可达集，最后给出两个仿真实例验证所得结果的有效性。

1 问题描述

考虑变时滞离散系统

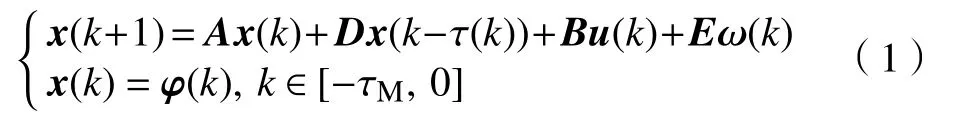
式中：x(k)=[x1(k),x2(k),···,xn(k)]T∈Rn为系统的状态向量；u(k)为输入向量；A,D,B和E为适当维数的常矩阵；τ(k)为时变时滞，且满足0＜τm≤τ(k)≤τM，τm,τM为非负整数。

初始条件 φ(k)满足

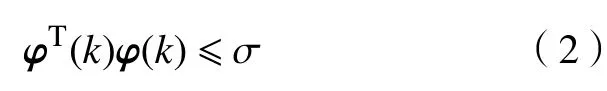
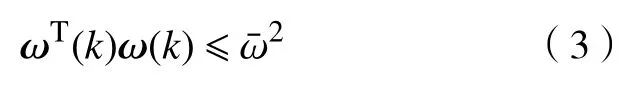
定义1在有界扰动下，系统（1）的可达集为

定义2对于矩阵P＞0，椭球的定义如下

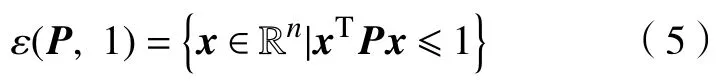
对于系统（1），考虑如下形式的状态反馈控制器

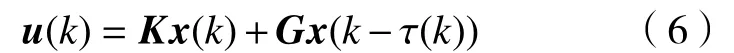
式中，K和G为待定控制器增益矩阵。

将状态反馈控制器式（6）代入系统（1），可得如下闭环系统

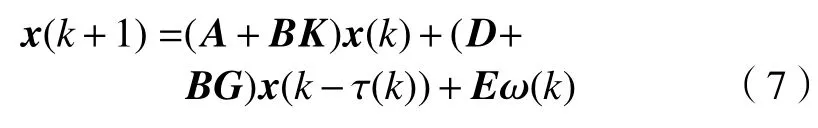
定义3令，称,λ1,λ2,···,λn是A的特征值}为矩阵A的谱半径。若ρ(A)＜1，则称矩阵A是Schur稳定的。

本文的主要目的是设计一个状态反馈控制器，使闭环系统的可达集包含在椭球体中，并且椭球体尽可能小。因此，为了得到本文主要结果，首先给出引理1和引理2。

引理1[14]设V(x(k))是满足的Lyapunov泛函，且V(x(k))＞0。若存在标量0＜α＜1使得

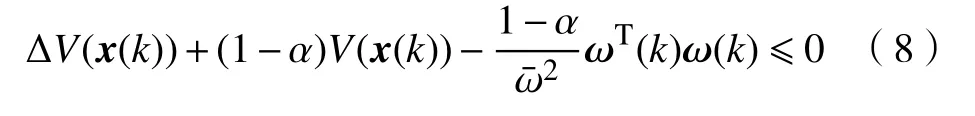
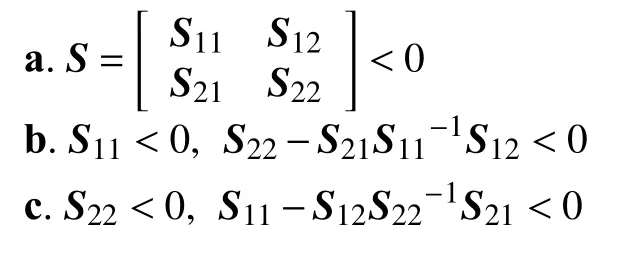
2 主要结论

2.1 可达集的椭球界

本文旨在设计一个状态反馈控制器（6），使得闭环系统（7）的可达集包含在椭球里面，并且该椭球要尽可能的小。以下定理给出系统（1）～（3）可达集椭球界存在的充分条件。

定理1考虑在有界峰值扰动（3）下的系统（7），若存在正标量λ1,λ2,λ3,λ4，矩阵＞0，＞0，＞0，＞0,L,R及标量0＜α＜1，满足

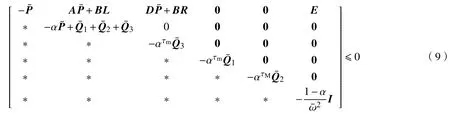
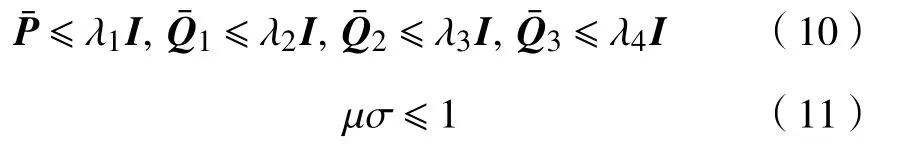
其中

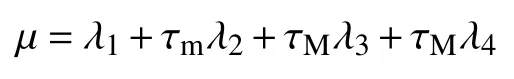
那么，存在状态反馈控制器（6），使得闭环系统（7）的可达集包含在椭球中。

证明选取如下Lyapunov-Krasovskii泛函：

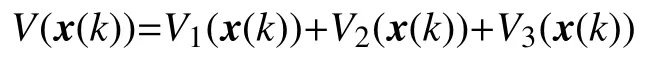
其中

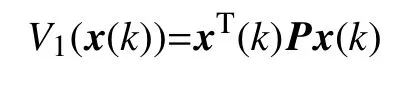
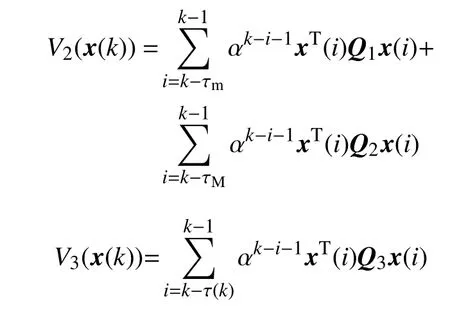
定义 ΔV(x(k))为V(x(k))的向前差分，则

不论是硬件方面在全市率先定标检测室样板间，还是软件方面创新开发APP及政府文化建设，江岸食药监局始终不忘初心，以归零心态重新出发，奋力拼搏赶超，农残检测工作再次走在全市前列。

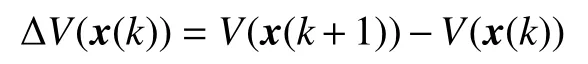
那么

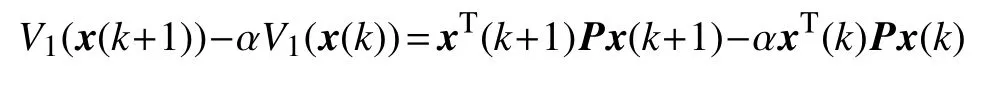
为了简便，式（8）记为

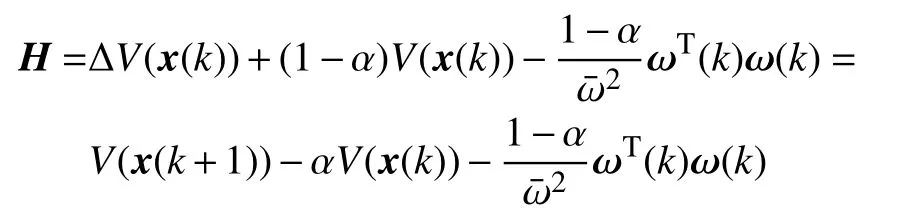
运用引理1，可得

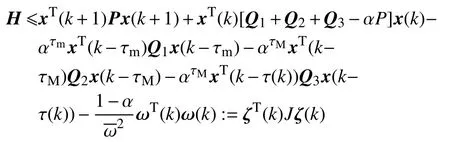
其中

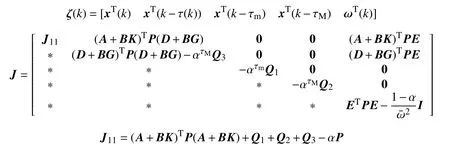
若J≤0，运用Schur补引理，可得

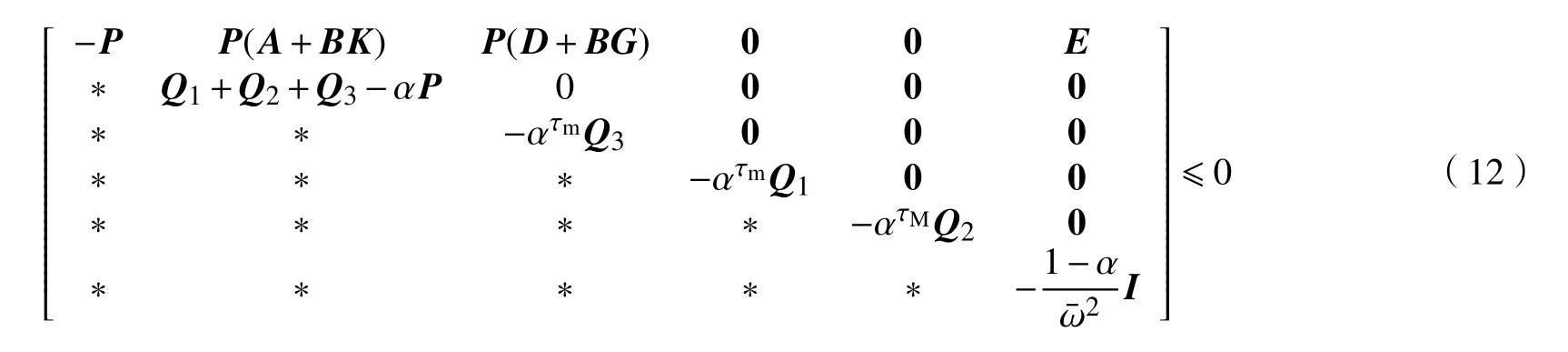
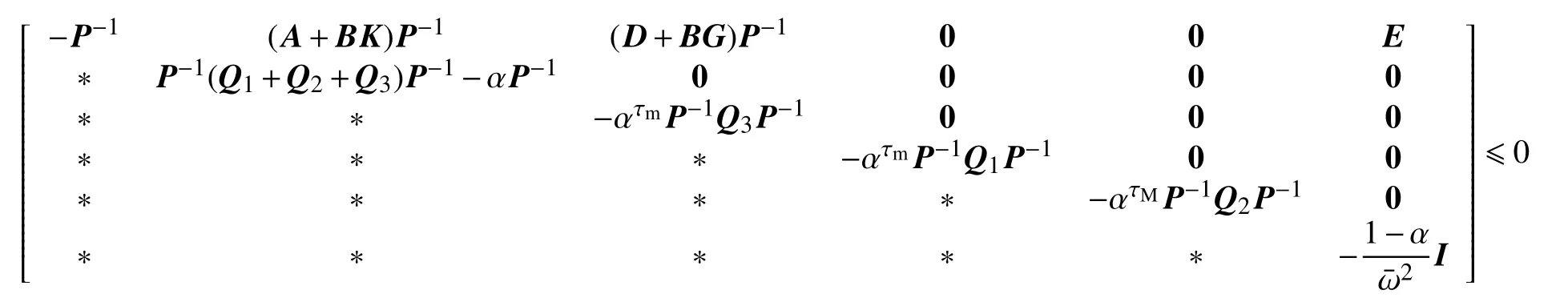
进一步，考虑Lyapunov泛函初值V(x(0))

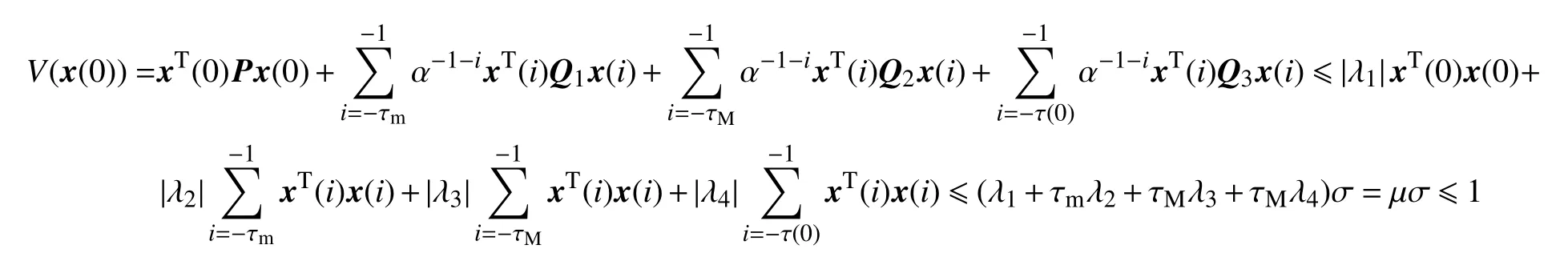
由条件（10）～（11）和引理2可知，

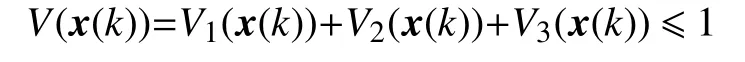
由于V2(x(k)),V3(x(k))≥0，所以V1(x(k))≤1。即，xT(k)Px(k)是椭球ε(P,1)的内部。由此可以得出结论：系统（7）的可达集包含在ε(P,1)中。定理1证毕。

在状态反馈控制器设计过程中，开环系统不一定稳定，只需满足定理1中的相关条件，就可以为系统设计控制器，得到稳定的闭环系统。

定理1中得到的条件不是LMI，因为它包含决策变量的乘积。然而，如果标量 α是固定的，则式（9）中的条件对于矩阵变量也是线性的。

为了求解带有参数λ1,λ2,λ3,λ4的矩阵不等式式（10），首先要将其转化为LMIs的形式。例如，不等式可表述为线性矩阵不等式，记=diag(λ1,λ1,···,λ1)。其中被定义为一个矩阵变量，并且依赖于决策变量λ1。

系统（13）优化问题可以转化为

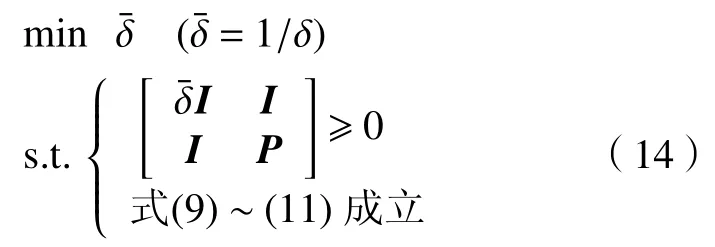
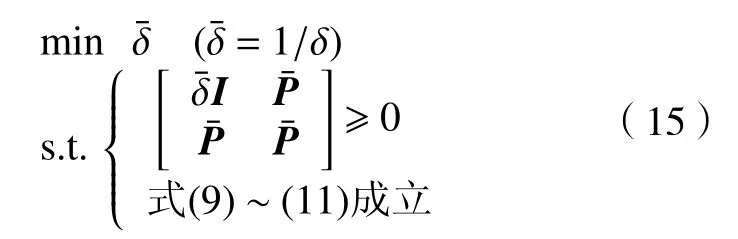
2.2 算法描述

定理1给出了有界扰动下闭环系统的可达集的界定条件，通过上述优化方法可以对边界椭球进行优化。然而，定理1中的结果是一个包含非凸标量 α时滞相关的矩阵不等式，通过固定α，可以使该问题转化为求解线性矩阵不等式（LMI）。

为了获得可达集的最小椭球，必须确定最优的标量α，这可以通过遗传算法（GA）来实现。算法如下：

a. 在（0, 1）中随机生成α，每个 α都是GA种群的一个个体；

b. 对于每个α，利用mincx. 求解包括变量的LMI优化问题，得到最优的；

c. 设置最大代数，如果达到该数字，则GA终止，否则，继续GA过程；

d. 根据每个α 的适应值，以概率选择下一代个体；

e. 根据给定的概率对新一代进行交叉和变异操作；

3 数值算例

本节给出两个数值实例来验证结果的有效性。

例1考虑时滞离散系统（1），系统参数为

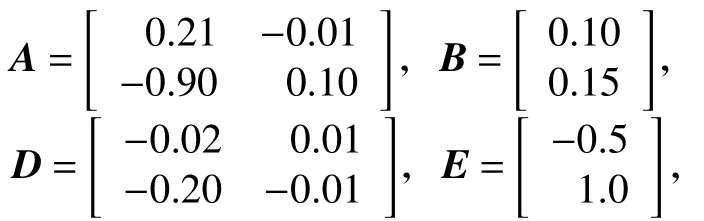
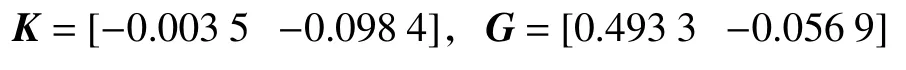
由定理1得到的边界椭球以及闭环系统的状态如图1所示。由图可见，闭环系统的状态包含在椭球ε(P,1)中。

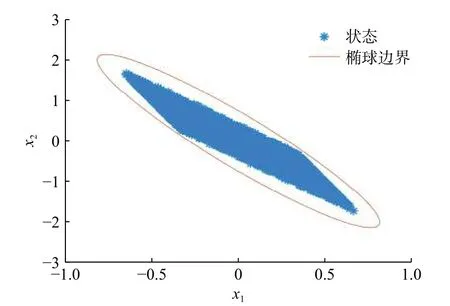
图1 可达集和椭球边界（例1）Fig.1 Reachable set and ellipsoidal bound (Example 1)

例2 考虑时滞离散系统（1），系统参数如下：

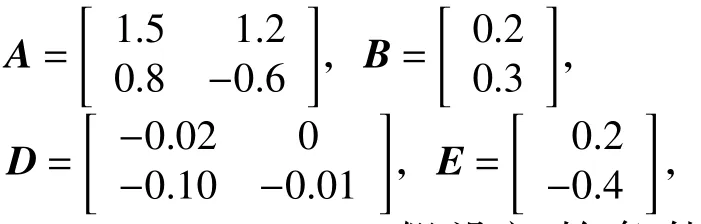
注意到，例2中A不是Schur稳定矩阵，因此开环系统的可达集不能被任何椭球体所界定。所以可以通过设计状态反馈控制器，处理闭环系统的可达集估计问题。

通过求解优化问题（15），计算结果如下：

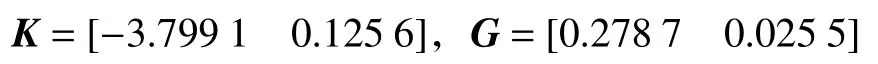
由定理1得到的椭球边界以及闭环系统的状态如图2所示。由图可见，闭环系统的状态包含在椭球ε(P,1)中。

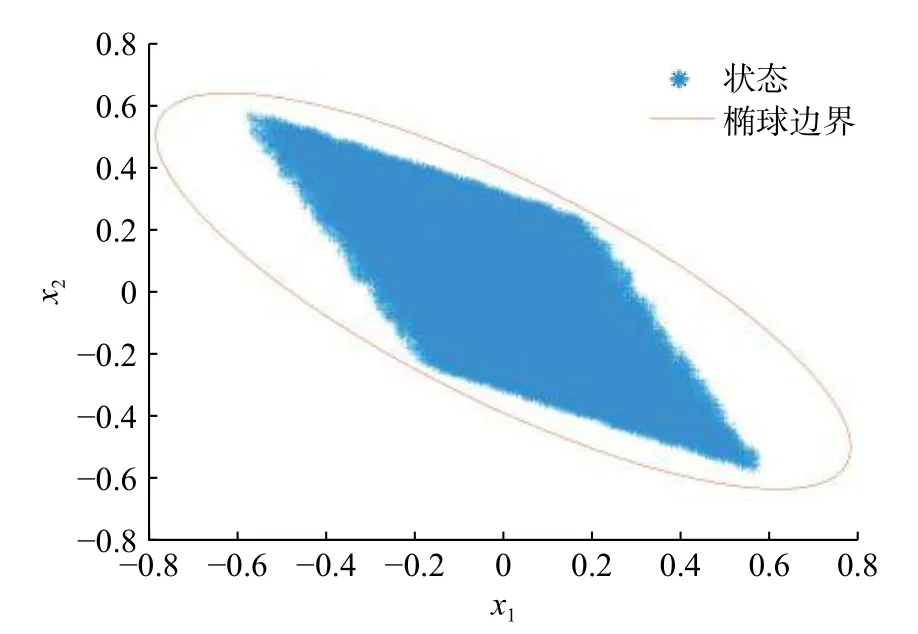
图2 可达集和椭球边界（例2）Fig.2 Reachable set and ellipsoidal bound (Example 2)

4 结 论

研究了在有界峰值扰动下离散变时滞系统的可达集估计问题，且系统的初值不必为零。通过设计状态反馈控制器，将系统由开环系统转化为闭环系统。随后，利用Lyapunov-Krasovkii泛函方法给出了闭环系统可达集的椭球边界。为了使该椭球体尽可能小，提出了优化方法。在此过程中，采用遗传算法求解最优参数，数值算例验证了本文所得结果的有效性。