民用飞机主最低设备清单建议稿项目模糊综合评价方法研究

2021-11-01顾志武杜倩宜冯蕴雯薛小锋

航空工程进展 2021年5期

顾志武，杜倩宜，冯蕴雯，薛小锋

（1.上海飞机客户服务有限公司飞行运行支援部，上海200241）

（2.西北工业大学航空学院，西安710072）

0 引言

随着我国民用飞机制造技术的发展，具有自主知识产权的国产民用飞机正逐步大量投入使用。民用飞机在满足安全性的前提下，重点需对其运营经济性进行充分考虑，确保民用飞机运营能够实现高安全性和高签派率［1］。主最低设备清单建议稿（Preliminary Master Minimum Equip‐ment List，简称PMMEL）用于平衡民用飞机的安全性和经济性，旨在保证安全飞行的前提下提高民用飞机的签派率，故确定PMMEL是目前保障民用飞机运营阶段安全经济不可或缺的必要环节。

传统的PMMEL项目分析方法主要有对比经验法、安全性分析法和逻辑决断分析法。许科龙［2］最早提出对比经验法和逻辑决断分析法作为PM‐MEL项目评价的方法；张瑞华［3］利用对比经验法分析了某型飞机的液压系统PMMEL项目；汪震宇等［4］利用安全性分析法对发动机舱火警测探器进行分析，得出PMMEL候选项目评估结果；包丽等［5］用逻辑框图联系功能危险分析、故障模式影响分析、故障树分析三种安全性分析方法，形成了具有可执行性的逻辑决断分析法。在传统的PM‐MEL项目分析方法中，对比经验法凭借相似机型类比分析确定PMMEL候选项目，仅依靠经验判定难以确定评价结果的准确性和可靠性；而逻辑决断分析法结合了常用的三种安全性分析方法，评判过程较为复杂，不利于实际的工程应用。模糊综合评价法可以对与多种评价因素有关的目标计算得到一个具体的评价结果，具有评价结果明确的特点，现已广泛运用于质量控制、资源管理等多种工程领域［6-8］。

针对现有PMMEL候选项目评价方法中存在的问题，本文提出一种基于模糊综合评价的PM‐MEL候选项目评价方法，对经过初期定性分析筛选的PMMEL候选项目进行评价，将专家对不同PMMEL候选项目的评分数据作为输入的原始数据，建立PMMEL模糊综合评价模型，根据评价结果判定该PMMEL候选项目是否纳入到PMMEL中；并对某型民用飞机主起落架下位锁弹簧PM‐MEL候选项目进行模糊综合评价，与经典FMEA分析方法得到的结果进行对比，以验证该评价模型的可行性和准确性。

1 模糊综合评价理论

1.1 模糊综合评价

模糊综合评价法可以对与多种因素有关的对象做出一个具体的评价［9］。若有一个需要评价的项目X，需要确定被评价对象的所有评价指标（因素），并建立评价因素论域U。假设有n层因素隶属层级，则评价因素论域U=（U1，U2，…，U i，…，U n），其中U i=（U i1，U i2，…，U im）（i=1，2，…，m）表示具有m个评价指标的第i层因素集；U ij表示第i层的第j个评价指标。一般评价因素论域确定顺序由第一层开始逐层向下分解，直到分解出整个体系的最后一层指标为止。为了反映各因素的重要程度，对各因素U ij分配一个相应的权数aij（i=1，2，…，n；j=1，2，…，m），一般要求aij满足aij>0，∑aij=1，再由各权重aij组成一个矩阵A，称为模糊权重矩阵。

确定评价指标（因素）及权重之后，需要进一步确定评价等级论域。评价等级是评价者对被评价对象在某因素条件下可能作出的各种评价结果的集合，评价等级集合V=（v1，v2，…，vl）本质上就是对被评价对象变化区间的一个划分，其中vp（p=1，2，…，l）表示第p个评价结果，l为总评价结果数。然后进行单因素模糊评价，建立模糊关系矩阵R。先基于一个因素进行相应的评价，确定目标对评价集合V的隶属度，称为单因素模糊评价。

在进行了单因素模糊评价后，逐一对研究目标在每个评价因素U ij（i=1，2，…，n；j=1，2，…，m）上进行评价，从一个评价因素出发确定目标对模糊子集的隶属程度，就是模糊关系矩阵：

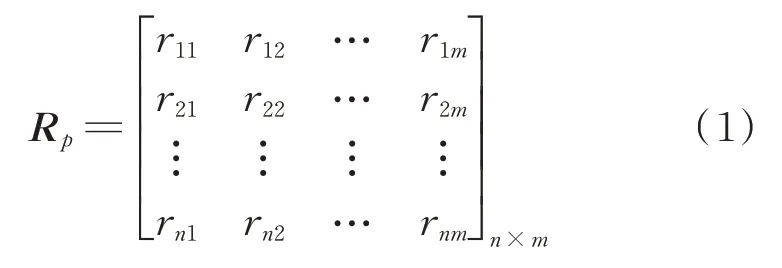
矩阵R p中第i行第j列元素r ij，代表某个目标基于因素U ij对vp的隶属度。目标在某个评价因素U ij上的评价结果，反映在模糊向量（R|U）上，而其他的评价方法都是由实际参数值反映出来的，因此，从这个角度讲模糊综合评价要求更多的信息，具有结果清晰、系统性强的特点。

最后，得到模糊权向量A与模糊关系矩阵R通过模糊算子计算得到模糊综合评价结果向量B。该模型为

式中：bj（j=1，2，…，m）是由A与R通过模糊合成算子得到的，表示被评级对象从整体上看对V评价等级的隶属程度。

用到的模糊合成算子是M(∧，∨)算子

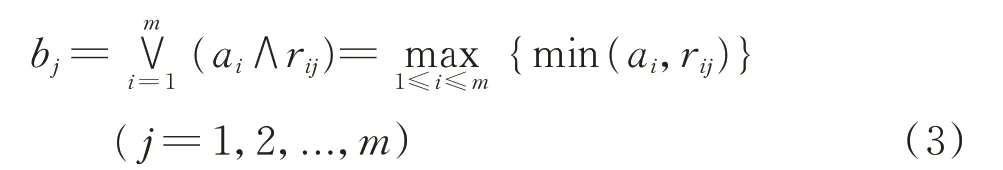
得到模糊综合评价结果向量B后，运用加权平均原则分析模糊综合评价结果，将B中对应分量各等级的秩逐级进行加权求和，最终得到被评价对象在等级论域中的相对位置，即为被评价对象的评价结果。

1.2 层次分析法

层次分析法（Analytic Hierarchy Process，简称AHP）是一种结合了定性分析和定量分析的考虑多因素的分析方法［10］，被广泛应用于指标权重的确定［11］。该方法把研究对象中考虑的多因素进行有序层次分析，可以对需要进行定性判断但考虑因素众多且没有大量数据支撑的问题有一个合理的解决。层次分析法在定量分析方面主要用判断矩阵构造的方法［12］，具有简便、计算量小、小样本结果可靠等特点［13］。AHP的主要计算步骤为

步骤1收集模糊综合评价建立的因素论域及各层级间的隶属关系，构造递阶层次结构模型。

步骤2采用两两比较的方法，从最底层逐层进行比较判断，确定低层指标相对于存在隶属关系的上一层指标的重要性（采用1~9比例标度属于层次分析法通用比例标度表［14］），并构造判断矩阵G。层次分析法中的关键是判断矩阵的建立，根据模糊综合评价中所建立的因素集，建立判断矩阵，判断矩阵元素的值反映了专家对各元素相对重要性的认识，能够得到较为准确的权重［15］。若该层有n个因素则判断矩阵G为n×n矩阵。

步骤3对判断矩阵G正规化后进行一致性检验，当CR满足式（4）时，认为判断矩阵G是符合一致性要求的，反之则认为判断矩阵G不具有足够的一致性，需要再次调整。

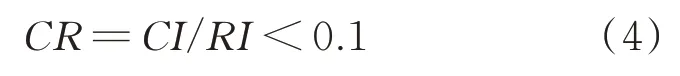
式中：CR为判断矩阵的随机一致性比率；RI为判断矩阵的平均随机一致性指标（RI值查表得到）；CI为判断矩阵的一致性指标。

式中：λmax为判断矩阵G的最大特征根；n为判断矩阵G的阶数。

步骤4解矩阵方程计算各级评价因素的权向量W：

式中：W为特征值λmax对应的特征向量，即所求的权向量。

2 民用飞机PMMEL项目模糊综合评价模型

2.1 PMMEL项目评价指标建立

本文建立用于PMMEL评价的三层级指标，对于第一层指标，飞机安全性的首要因素是飞机自身的机械原因，其直接决定了飞机的安全状态。其次，PMMEL项目涉及大量人员的操作内容，人为因素是造成飞机事故的主要原因，人员的影响不可忽视。此外，考虑到部分飞机对特殊环境飞行的适应情况以及特殊要求，环境也作为一大因素。因此PMMEL项目的制定是飞机、操作人员和环境的有机整体，故PMMEL项目评价第一层指标一般为U=｛飞机，人员，环境｝。

进一步建立评价指标中的第二层指标。针对第一层指标U中的飞机，飞机的机械安全性则需分别探究是否具有冗余性设计，以及该项目设备失效后造成的安全性和维修可靠性方面的问题，即U1=｛U11，U12，U13｝=｛冗余性，安全性，维修可靠性｝。对于第三层级评价指标，飞机设备或项目的冗余性，可以考虑在飞机设计初期就对该系统有冗余性系统设计或飞机上具有针对该系统的功能替代设备，即U11=｛冗余性系统设计，功能替代设备｝；飞机的安全性，可以考虑某PMMEL候选项目在失效后的故障影响和继发故障影响，即U12=｛故障影响，继发故障影响｝；飞机的维修可靠性，则仅考虑飞机的保障率，具体可指飞机的签派可靠度、平均故障时间等指标，即U13=｛飞机保障率｝。

同理，针对第一层级指标中的人员，则需同时考虑机组人员和维修人员两方面的影响，即U2=｛U21，U22｝=｛机组人员，维修人员｝。机组人员应当考虑到某PMMEL项目失效后的操作程序（O）以及对机组人员工作负荷是否增加、增加的程度是否可接受，即U21=｛操作程序（O），机组人员工作负荷｝；维修人员则考虑某PMMEL项目失效后维修人员应遵守的维修程序（M），即U22=｛维修程序（M）｝。

针对环境指标，应考虑民用飞机运行过程中需要面对的特殊飞行环境，即U3=｛U31｝=｛特殊环境｝。环境指标应根据具体进行型号审定的航空器部件进行具体的分析，例如特殊环境下还可细分为高温环境、高原环境等。

2.2 PMMEL项目评价等级标准划分

对PMMEL项目进行最终评价的目的是明确某系统或部件项目是否纳入到PMMEL中。因此，将评价等级论域定义为3个等级，即

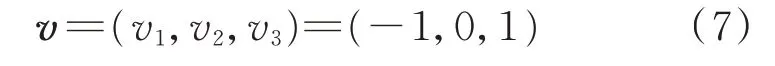
对应描述为v=｛低风险，可接受，高风险｝，根据描述表示是否将某系统或部件项目纳入PM‐MEL的危险等级。（-1，0，1）实际表示的是模糊数，并根据数值确定相应的风险等级，目的是达到对评语进行量化处理确定评语等级论域，即建立评价集：

对应的评价定量等级标准如表1所示。

表1 PMMEL项目模糊综合评价定量等级标准Table 1 Fuzzy comprehensive evaluation quantitative grad‐ing standard of PMMEL

2.3 PMMEL项目模糊综合评价步骤

PMMEL项目模糊综合评价分为五个具体的步骤：确定评价对象、计算评价指标权重、建立模糊关系矩阵、计算综合评价向量以及对评价结果进行判定。PMMEL项目模糊综合评价步骤如图1所示。

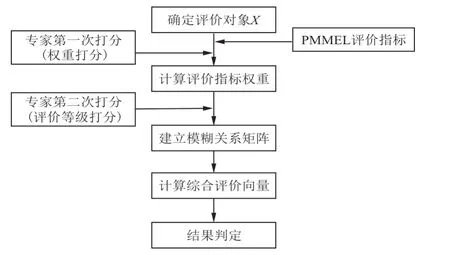
图1 PMMEL项目模糊综合评价步骤Fig.1 Fuzzy comprehensive evaluation steps of PMMEL

步骤1确定评价对象X。评价对象为某具体系统或设备的PMMEL候选项目，即经过定性分析后仍不确定其失效危险等级，故不能确定是否列入PMMEL中。

步骤2计算评价指标权重。对PMMEL候选项目的评价因素集进行权重系数计算，运用层次分析法，采集专家及相关人员对各因素指标的评价结果，自上而下构造各级判断矩阵，检验其是否满足一致性要求，计算得到权重向量W，组合得到模糊权重矩阵A。

步骤3建立模糊关系矩阵。根据评价等级论域，结合专家评价结果，可邀请多位专家进行PMMEL项目评价（PMMEL项目专家评价表如表2所示），建立各级模糊关系矩阵R。

表2 PMMEL项目模糊综合评价专家评价表示例Table 2 Fuzzy comprehensive expert evaluation sheet of PMMEL

步骤4计算综合评价向量。根据步骤2得到的模糊权重矩阵A和步骤3得到的各级模糊关系矩阵R，通过模糊综合评价模型A⋅R=B，自下而上计算模糊综合评价结果向量B。

步骤5结果判定。运行加权平均原则，将步骤4得到的模糊综合评价结果向量B中对应分量各等级的秩逐级进行加权求和，最终自下而上计算得到被评价对象在等级论域中的相对位置，即为被评价对象PMMEL候选项目X的评价结果，即将此系统或设备列入PMMEL中是否可接受。

3 飞机主起落架下位锁弹簧PM⁃MEL项目评价案例分析

3.1 确定评价对象

根据世界民航事故数据库相关资料的统计结果，起落架收放系统发生故障时引起的Ⅰ类、Ⅱ类事故较多，是民用飞机安全性分析的重点。Boe‐ing 737等机型将起落架收放功能等相关项目作为PMMEL，MMEL和MEL项目［16］。同时，中国民用航空规章CCAR-25-R4中对起落架的设计做出了明确规定和要求［17］，在起落架收放系统可能发生的众多故障类型中，“起落架不能放下或放下未锁定”故障等级为危险级，指标要求为10-7/fh。故本算例选取某型民用飞机主起落架系统中下位锁弹簧作为PMMEL候选项目，即X为主起落架下位锁弹簧。

3.2 指标权重计算

为了计算针对某型飞机主起落架下位锁弹簧PMMEL候选项目评价分析因素的模糊权重向量，首先构建层次分析法递阶层次结构如图2所示，在本案例中不考虑具体的运行环境影响。

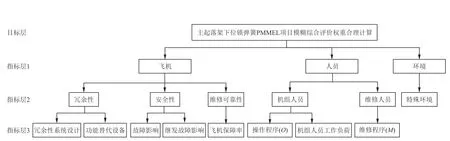
图2 PMMEL评价指标递阶层次结构图Fig.2 Hierarchical structure of PMMEL fuzzy comprehensive evaluation factors

以指标层1的模糊权重向量为例，首先对某专家通过两两比较得到的数据信息进行处理，使专家打分数据能够准确地构造出指标层1判断矩阵S=(uij)p×p(i=1，2，3；j=1，2，3；p=3)即：

计算判断矩阵S的最大特征根λmax=3.038 5，由式（5）可知，一致性指标为0.019 25，查表不同阶判断矩阵的平均随机一致性指标RI，阶数为3的判断矩阵RI=0.58，计算CR为

显然，CR小于0.1，故认为判断矩阵S是符合要求的，即具有足够的一致性，最大特征根λmax对应的特征向量W为

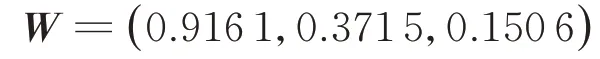
计算得到正规化后的特征向量W1为

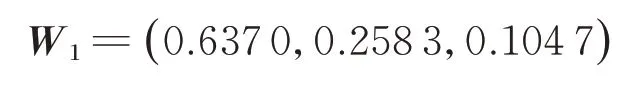
同理计算得到指标层2和指标层3的模糊权重向量，正规化后得到飞机主起落架下位锁弹簧PMMEL候选项目评价分析因素的模糊权重如表3所示。

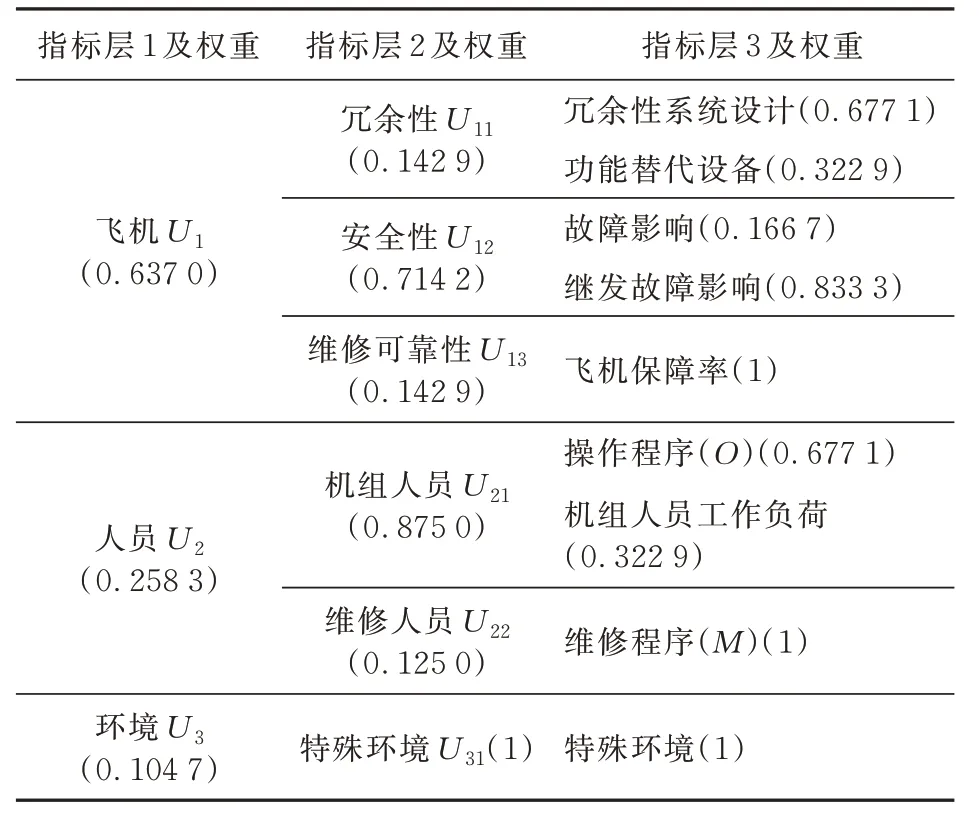
表3 评价指标权重表Table 3 The weight of fuzzy comprehensive evaluation factor

3.3 PMMEL项目评价计算

将来源于有关专家的统计数据（如表4所示）建立各三级子因素的模糊关系矩阵R，专家评价规则按照：若因素与评语完全符合则给定数值为1，完全不相似则给数值0，其余按照相似程度给出0~1之间的数值。

表4 专家评分表T able 4 Fuzzy comprehensive expert evaluation sheet

由专家评价数据表提取出各级因素与评价域的模糊关系矩阵，以冗余性的三级因素为例。冗余性的三级因素可以表示为U11=｛冗余性系统设计，功能替代设备｝与V=｛V1，V2，V3｝=｛低风险，可接受，高风险｝的模糊关系矩阵R11为

同理得到安全性U12的三级因素、维修可靠性U13的三级因素、机组人员U21的三级因素、维修人员U22的三级因素、飞机U1的二级因素、人员U2的二级因素、环境U3的二级因素与V=｛V1，V2，V3｝=｛低风险，可接受，高风险｝的模糊关系矩阵分别为

得到各级模糊关系矩阵后，利用模糊综合评价模型A⋅R=B，求得相应的模糊综合评价结果向量为

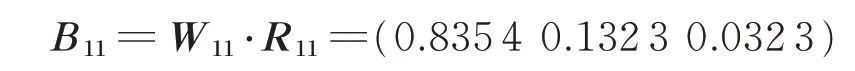
同理求得其他模糊综合评价结果向量为

3.4 评价结果分析

根据得到的评价结果向量，进行综合评分值V的计算，具体计算公式为Vi=v B（v=（-1，0，1）），自下而上首先对三级因素综合评分值进行计算，得到结果为

由上述计算对照评价定量分级标准，五个二级因素子集均为E1等级，则表示接受主起落架下位锁弹簧列入PMMEL项目为低风险事件。

其次对二级因素综合评分值进行计算，得到结果为

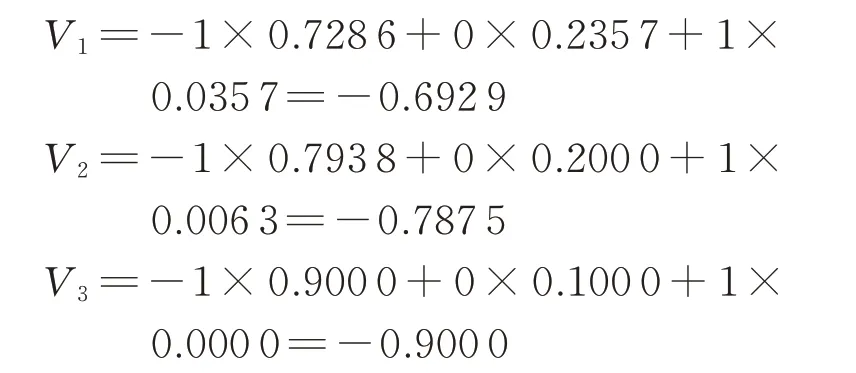
由上述计算对照评价定量分级标准，三个一级因素子集均为E1等级，则表示接受主起落架下位锁弹簧列入PMMEL项目为低风险事件。

最后对总体因素综合评分值进行计算，得到结果为

说明将主起落架下位锁弹簧列入PMMEL事件风险属于E1级。因此，根据模糊综合评价的结果，该机型的主起落架下位锁弹簧在纳入PMMEL项目时，其风险低于可接受等级，亦表示能够接受该部件列入PMMEL项目，进而说明基于模糊综合评价方法对PMMEL项目进行评价的可行性。

若有多位专家进行评价，则需将多位专家打分取平均值后再按照模糊综合评价结果计算流程计算专家评价最终结果，以此来确保专家打分方法的可信度和准确度。

对主起落架下位锁弹簧PMMEL候选项目用传统的安全性分析方法FMEA，并通过逻辑决断分析，得到主起落架下位锁弹簧FMEA分析结果（如表5所示）以及是否允许列入PMMEL中。锁弹簧的FMEA分析故障等级为Ⅱ，在有运行程序或操作程序能够使飞机保持在放飞的安全水平时，能够继续出勤或继续飞行，并且同一侧主起落架两个弹簧不允许同时失效，即只允许单个锁弹簧失效。根据PMMEL项目确定决断分析法分析可知，主起落架锁弹簧可列为PMMEL项目。由此验证了模糊综合评价法对PMMEL项目评价具有准确性［18-20］。