能量收集认知多跳中继网络中断性能分析及优化

罗 轶 孔静恬 董 健 佘青青 黄 慧 黄正宇

①(湖南师范大学智能计算与语音信息处理湖南省重点实验室 长沙 410081)

②(中南大学计算机学院 长沙 410075)

③(华南理工大学电子与信息学院 广州 510641)

1 引言

为了使能量受限无线系统实现自持运行，射频能量收集(Radio Frequency Energy Harvesting,RF-EH)技术[1,2]在近几年得到深入研究。随着源节点和目的节点间距增大，两跳中继网络(Relay Networks,RNs)已不能满足通信要求[3]，因此近来具有RF-EH的多跳RNs已引起广泛关注。文献[4]讨论了采用携能通信方式以及两种中继协议从相邻节点收集能量的多跳RNs最大吞吐量。同时为了提高频谱利用率，认知无线电与多跳EH-RNs结合，形成了新的能量收集认知多跳中继网络(Energy Harvesting Cognitive MultiHop Relay Networks,EH-CMHRNs)。文献[5]推导了具有单主发送端(Primary Transmitter,PT)和主接收端(Primary Receiver,PR)的EH-CMHRNs中断概率。文献[6]研究了协作多跳EH-CRNs在联合功率分配和路径选择下的次网络(Secondary Network,SN)中断性能。文献[7]则提出了由中继簇构成的多跳EH-CRNs，并推导了SN中断概率和吞吐量的解析式。与文献[2]和文献[4–7]中采用从主网络(Primary Network,PN)或SN节点收集能量方式不同，文献[8]采用功率信标(Power Beacon,PB)为具有单PR的EH-CMHRNs提供能量。文献[9]则构建了一个具有多PR的多PB辅助EH-CMHRNs，并采用自适应权重粒子群算法对SN中断性能进行优化。Poornima等人[10]则分析了具有多PR和PT的PB辅助EH-CMHRNs中断性能。文献[11]讨论了具有单PR的PB辅助EH-CMHRNs在κ-μ衰落信道下的SN中断性能。文献[12]则将EH-CRNs拓展到了物联网应用领域，构建了PB辅助能量收集认知多跳蜂窝式设备到设备通信系统模型。值得注意的是，以上文献研究均假设RF-EH电路始终处于激活状态，SN节点总能实时获取其到PR链路的瞬时信道状态信息(Channel State Information,CSI)。但在实际网络中，信道衰落严重或SN与PN间协作不佳，导致RF-EH电路不能被激活或完整CSI无法实时获取。

与上述文献所作的研究不同，本文的创新点和贡献如下：(1)构建了新的具有PN干扰的PB辅助能量收集认知多跳中继网络模型，SN节点同时从PB和PT节点射频信号中收集能量。(2)从工程应用实际出发，模型采用较易获得的干扰链路统计CSI，并考虑了接收信号功率过小无法激活SN节点RFEH电路所导致的SN功率中断问题。(3)推导出了SN功率中断概率、信道中断概率和总中断概率的精确和渐近闭合式，并采用自适应混沌粒子群优化(Adaptive Chaos Particle Swarm Optimization,ACPSO)算法对SN总中断概率进行优化。

2 网络模型

图1 网络模型

假设SN和PN之间协作受限，Rk只能获得其到Dn链 路的统计CSI，且受Dn所能容忍的最大干扰信号功率(PN干扰约束)PI限制，Rk的发射功率PT,k服从[13]

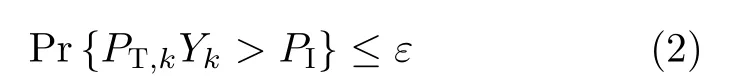
其中，ε为容忍误差，。Yk的累积分布函数(Cumulative Distribution Function,CDF)和概率密度函数(Probability Density Function,PDF)分别为

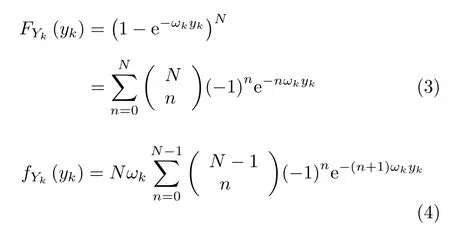
根据式(2)和式(3)，PT,k可计算为

由于Rk的发射功率还受其收集到的能量限制，所以Rk的实际发射功率为

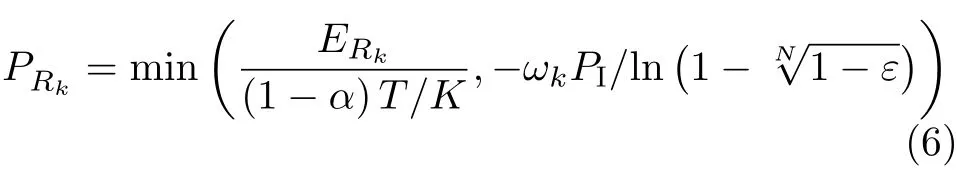
Rk+1的接收信干噪比(Signal-to-Interferenceplus-Noise Ratio,SINR)为

3 SN总中断概率分析

在本文网络模型中，SN传输发生中断的原因主要是以下两点：(1)Rk的RF-EH电路未被激活导致的功率中断；(2)SN数据传输链路信道质量不佳所致的信道中断。

在RF-EH系统中，节点接收的信号功率必须不小于阈值ζ才能激活RF-EH电路收集能量，ζ的取值范围一般为-30～-10 dBm[1]。本文将SN节点接收信号功率小于ζ的概率定义为功率中断概率。因此，Rk的功率中断概率为

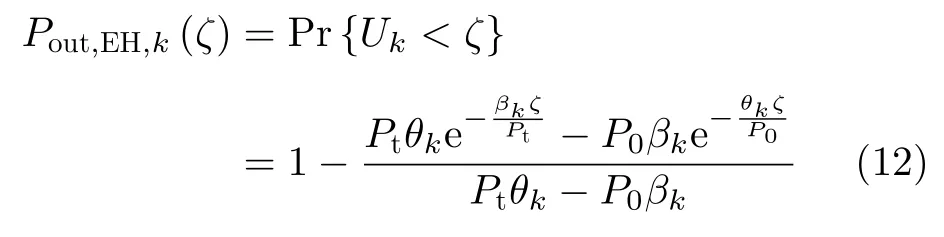
SN的功率中断概率则为

本文将SN的端到端SINR小于γth的概率定义为SN信道中断概率，可表示为

3.1 精确总中断概率

SN第k跳的精确信道中断概率可以表示为

其中，ϑ1(γth)和ϑ2(γth)可以分别计算为

依据文献[14]中的式(3.352.1)，式(18)可以写为

其中，E i(·)为指数积分函数。将式(16)代入式(14)可得SN精确信道中断概率Pout,C(γth)。将式(14)和式(13)代入式(15)可得SN的精确总中断概率Pout(ζ,γth)。

3.2 渐近总中断概率

当PI≪Pt+P0时，式(16)可以改写为

将式(20)代入式(14)中的Pout,C,k(γth)，可得在严格干扰约束条件下的SN渐近信道中断概率和式(13)分别代入式(15)中的Pout,C(γth)和Pout,EH(ζ)，可得在严格干扰约束条件下的SN渐近总中断概率。

当PI≫Pt+P0时，式(16)可以改写为

依据文献[14]中的式(3.353.3)，式(21)可以表示为

4 SN总中断性能优化

信道功率增益是服从指数分布的随机变量，难以具体确定，因此本文将α和Pt作为变量对SN的总中断概率进行优化，该最优化问题可以建模为

其中，Pmax为W发射功率的最大值，W为PB节点。

式(13)、式(17)和式(19)在形式上的复杂性，导致难以确定式(23)中目标函数的凹凸性，因此无法采用传统的凸优化算法对目标函数进行优化。为了解决SN的总中断概率最小化问题，本文采用ACPSO算法。与其它元启发式智能算法相比，ACPSO算法具有搜索过程的简单性、实现的容易性和收敛的快速性，特别是当需要优化的参数数目较少时，其运算的开销较低[15–17]。假设粒子的数目为S，粒子s,s∈{1,2,...,S}的位置和速度分别用xs,l和vs,l表示，l=1,2,xs,1和xs,2分别对应Pt和α，粒子s的速度和位置更新表达式分别为[15]

将xs,1(t)和xs,2(t)代 入式(23)，可得第t次迭代时，粒子s对应的SN总中断概率适应度fs(t)。其中，ωs(t)为粒子s在第t次迭代时的惯性权重。为了提高算法的全局搜索能力，同时避免陷入局部最优值，本文采用自适应权重法对ωs(t)进行自适应调整，ωs(t)为[16]

其中，L为总迭代次数。r1(t)和r2(t)为第t次迭代时[0,1]之间均匀分布的随机数。本文采用Tent混沌映射产生r1(t)和r2(t)，并对粒子群的位置和速度进行初始化，其迭代公式为

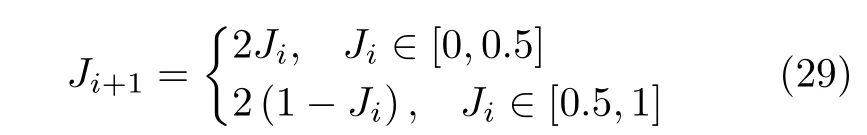
其中，Ji∈[0,1]，i=1,2,...。本文采用群体适应度方差φ(t)来 反映第t次迭代时的粒子群聚集程度，其定义为

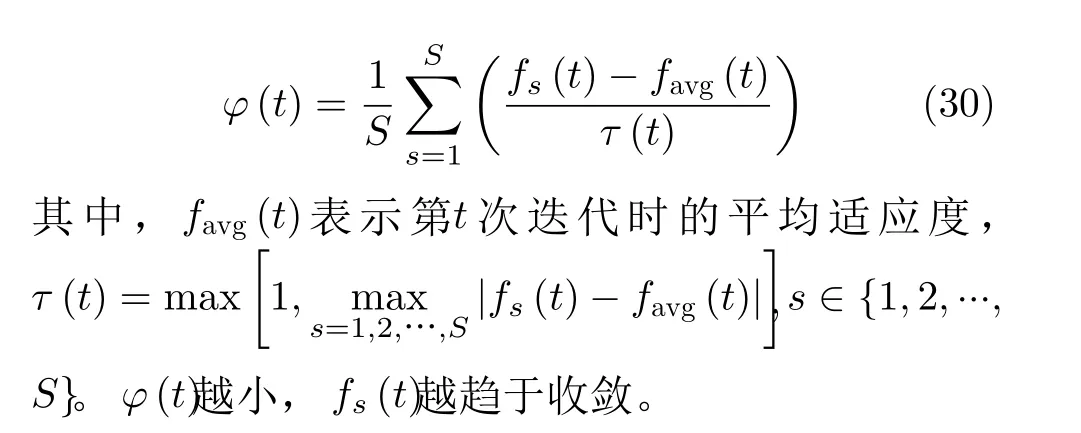
ACPSO算法的步骤如表1所示。

表1 ACPSO算法

式(23)在形式上比式(24)—式(30)复杂得多，以致ACPSO算法的复杂度主要由总中断概率适应度的计算次数所决定。假设在每一次迭代中每一个粒子总中断概率适应度的计算复杂度为H，若式(23)在第G*轮迭代后达到收敛，则ACPSO算法的计算复杂度可以表示为O(HSG*)。很显然，在粒子数目S给定且ACPSO算法能实现快速收敛的情况下，ACPSO算法的计算复杂度与H成正比。

5 仿真及分析

本节对SN中断性能进行了数值计算和 106次Monte Carlo仿真。除非另有说明，网络系统模型中的仿真参数设置如下：ζ=-10 dBm,ξ=2.5,η=0.8,K=2,α=0.3,Pmax=55 dBm,Rth=0.6 b ps/Hz,σ2=10-11,N=3,ε=0.3,S=50,l=2,L=50,R1,RK+1,W,B和Dn在X-Y平面上的坐标分别为(–1,0),(1,0),(0,1),(–1,1)和(1,1)，单位为m。R2～RK等间隔分布在R1和RK+1之间的X轴上。从图2—图7可以看出：Monte Carlo仿真曲线与理论分析的数值计算曲线高度吻合，从而证明了理论推导的正确性。

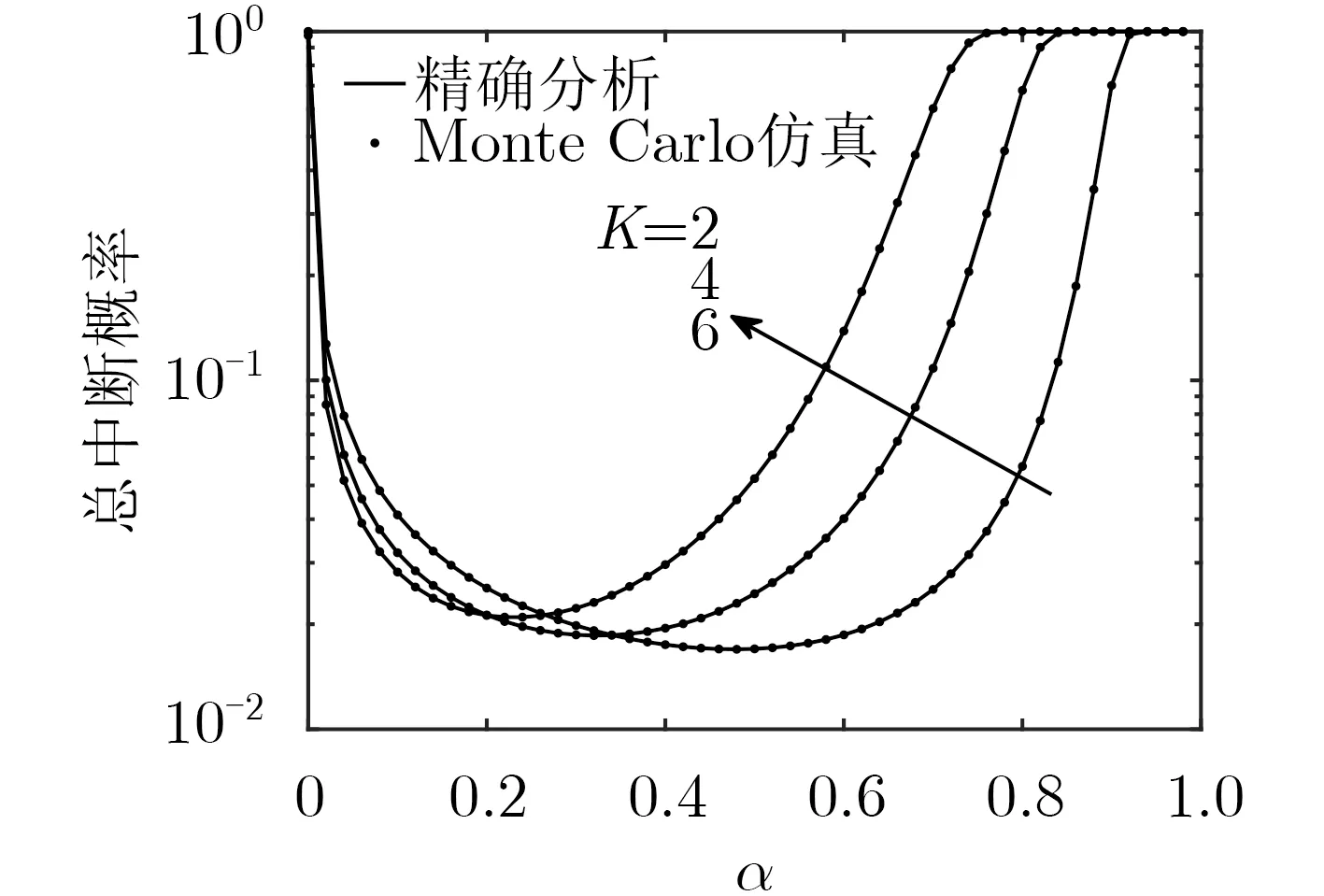
图7 SN总中断概率与α 间关系

图2表现了节点W和B在X-Y平面上不同位置时，SN功率中断概率与Pt间 关系。假设P0=1 dBm。从图2可以看出：(1)当节点W和B位置给定时，随着Pt增大，SN节点从W的射频信号中收集到的能量也会增大，导致SN功率中断概率降低。(2)当Pt给定时，SN节点会随着W和B与其的距离拉近而收集到更多能量，以致SN功率中断概率减小。

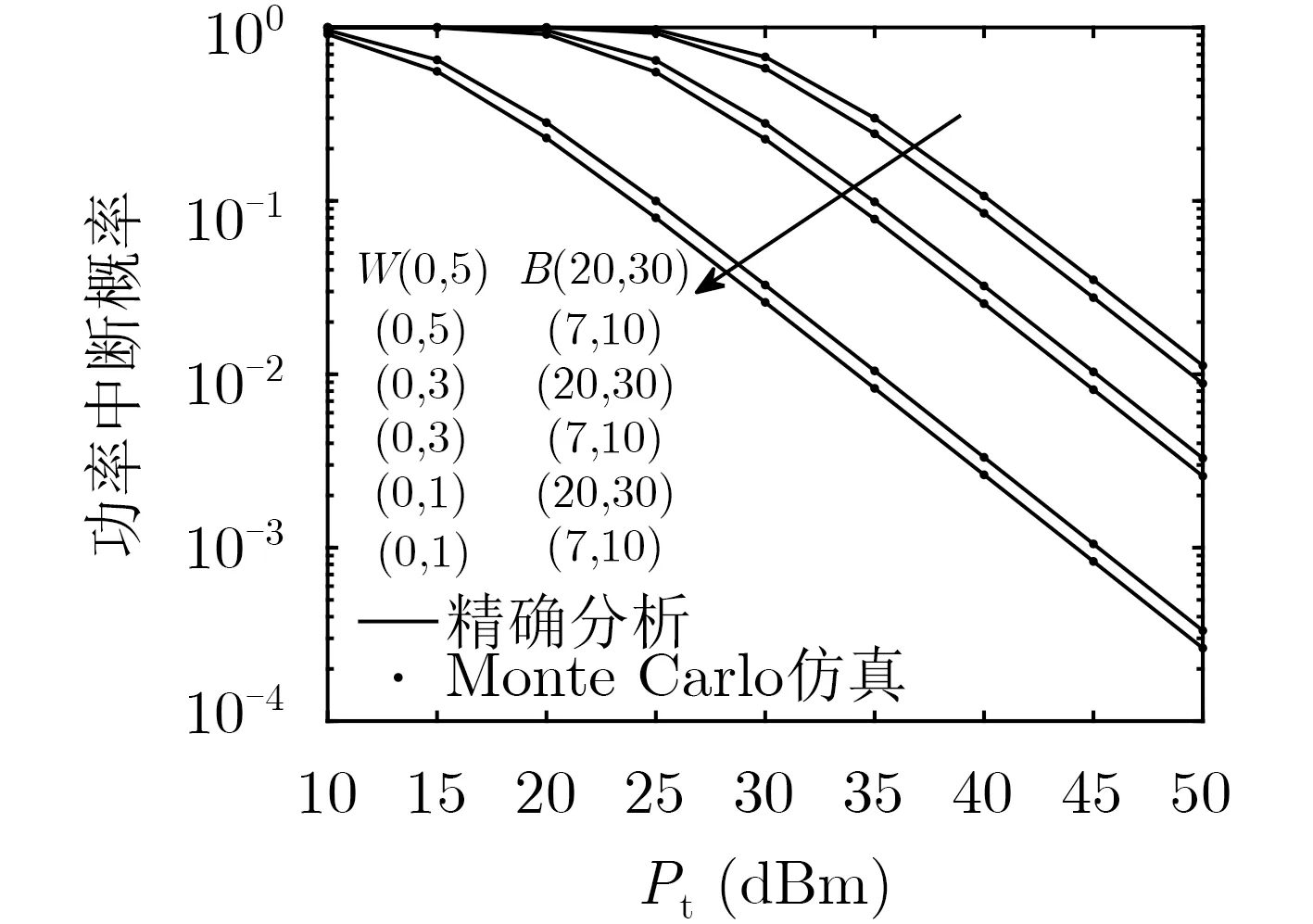
图2 SN功率中断概率与Pt间关系

图3和图4展现了N和ε取不同值时，SN信道和总中断概率与Pt间关系。假设P0=20 dBm,PI=30dBm。从图3和图4可以看出：(1)当节点B位置确定，N和ε值给定，且Pt较小时，；随着Pt的 增大，Pout,C和Pout均单调下降，并趋于饱和。(2)当N值增大时，SN节点到节点Dn的干扰链路具有较大信道功率增益的概率也会增大，Pout,C增加。(3)ε值的增加将使SN节点的发射功率增大，Pout,C降低。

图3 SN信道中断概率与P t间关系

图4 SN总中断概率与Pt间关系

图5表现了Rth和η取不同值时，SN总中断概率与PI间关系。假设P0=16dBm,Pt=50dBm,ε=0.1。从图5可以看出：(1)当Rth和η给定时，PI的增大使得Dn能够容忍Rk更大的发射功率，导致Pout单调下降，但Rk的发射功率受制于收集到的能量而不会无限增大，Pout最终将饱和。(2)当Rth给定时，η值越大，Rk收集到的能量就越多，Pout越小。(3)当η给定时，γth随着Rth的减小而减少，导致Pout降低。

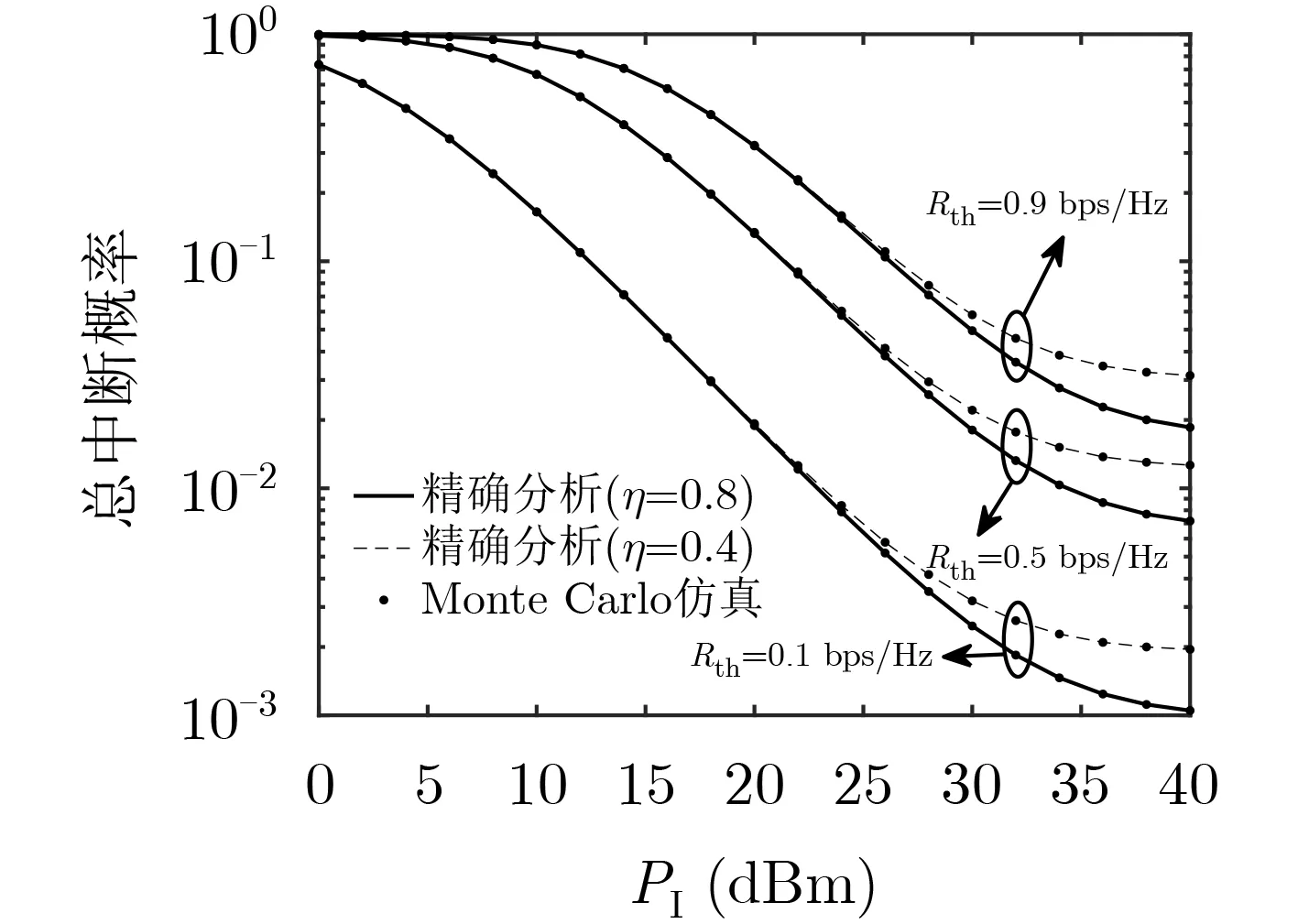
图5 SN总中断概率与PI间关系

图6体现了节点B处于不同位置时，SN总中断概率与P0间关系。假设PI=20dBm,Pt=30dBm。从图6可以看出：(1)当P0给定时，B与SN距离越近，其对SN的干扰就越严重，Pout就越大。(2)当B位置确定时，随着P0的增大，Pout单调上升，并最终趋近于1。因此，P0的增大虽有助于SN节点收集到更多能量，但其对SN的干扰将是主要的。

图6 SN总中断概率与P0间关系

图7给出了SN跳数K不同时，SN总中断概率与α间关系。假设PI=P0=10dBm,Pt=30dBm,R1和RK+1的坐标调整为(–3,0)和(3,0)。从图7可以看出：(1)当K值给定时，随着α的增大，Pout从1逐渐降低到最小值，随后又逐渐增大到1。(2)当K取不同值时，使Pout最小所对应的α值各不相同。因此，合理设置α和K值，都将有助于降低Pout。

图8展示了采用ACPSO算法和贪婪搜索算法进行优化以及未作优化时，SN总中断概率与PI间关系。假设Rth=0.9bps/Hz,P0=16dBm，未作优化时Pt和α固定取值为50dBm和0.3。从图8可以看出：(1)两种算法的计算结果完全一致，但后者因需在2维连续空间寻求Pt和α所对应的最小Pout，使得计算复杂度远高于前者。(2)当PI值给定时，采用ACPSO算法优化后的Pout明显小于未作优化的。如PI=20dBm时，ACPSO算法计算出的Pt,α和Pout分别为54.33dBm,0.42和10.22%，而未作优化时的Pout为32.21%。

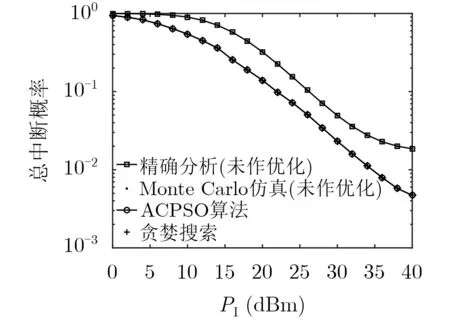
图8 优化算法下SN总中断概率与PI间关系

图9则表明了采用ACPSO算法和标准粒子群优化算法对SN中断概率进行优化时，SN中断概率适应度与迭代次数间关系。假设采用后者时，ωs(t)=0.8,c1(t)=c2(t)=0.5。从图9可以看出：(1)两者均能有效实现对Pout的优化。(2)前者和后者分别需要6次和22次迭代实现收敛。因此，相较于后者，前者具有更快的收敛速度和更好的稳定性。

图9 总中断概率适应度与迭代次数间关系

6 结束语

本文构建了新的具有单PT和多PR的PB辅助EH-CMHRNs模型，提出了具备能量收集的单向多跳中继传输方案，在考虑SN对PN干扰链路统计CSI场景下，推导了SN功率中断概率以及精确和渐近总中断概率闭合式，并采用ACPSO算法对网络参数进行优化。仿真结果表明：各网络参数对SN中断性能影响明显，ACPSO算法能快速和有效地实现SN总中断概率最小化。