基于改进迭代扩展卡尔曼滤波的3星时频差测向融合动目标跟踪方法

曲志昱 王超然 孙 萌

(哈尔滨工程大学 哈尔滨 150001)

(先进船舶通信与信息技术工业和信息化部重点实验室 哈尔滨 150001)

1 引言

星载无源定位系统因其具有探测距离远、监控范围广、不受地域国界影响、隐蔽性能好等优势，在电子对抗、侦察监视等领域[1–3]发挥着越来越重要的作用。近年来，随着星载电子侦察技术的发展，其定位体制日趋多样化[4]，定位目标也从最初的地面固定目标延伸至空域运动目标[5]。传统星载时频差无源定位算法应用于高速运动目标时，常忽略目标的运动速度，这会导致频差定位结果出现较大偏差[6]，另外，高速运动的目标一般都位于高空而非地表，但传统星载定位普遍利用假设高程的球面模型或椭球面模型，即通过假设目标高程为0的方式将地球表面视作定位面进而实现目标定位[7]。因此，对于搭载于高速运动平台(如战机、导弹等)上的辐射源目标而言，这些算法将不再适用。

文献[8]提出一种基于高程值估计的3星时频差运动辐射源定位方法，使用解析法实现了动目标的测速和定位，但精度较低，且随着辐射源高程的增加，定位、测速的误差会越来越大，文献[9]研究一种基于扩展卡尔曼滤波(Extended Kalman Filter,EKF)的时频差联合定位跟踪方法，改善了高速目标的速度带来的测量误差大的问题，但仍将目标高程假设为已知量参与跟踪计算；文献[10]提出一种基于时差频差的多站多次定位跟踪滤波方法，但该算法应用于星载3维定位时至少需要4个观测站，这将大大提升探测成本和卫星组网难度；文献[11]给出一种高精度测向辅助的3星时差定位算法，该算法通过引入方位角信息，使定位目标不再局限于地面辐射源，但由于缺乏对目标速度的直接观测，因此算法对动目标定位跟踪的效果较差。针对上述问题，本文在3星时频差定位系统基础上，提出了一种利用主星1维测向信息的改进迭代扩展卡尔曼滤波(Iterative Extended Kalman Filter,IEKF)融合跟踪算法，算法在EKF方法中加入迭代，后采用LM(Levenberg-Marquardt)方法[12]对迭代过程的状态更新进行优化，并给出了迭代终止条件。仿真结果表明，算法可以实现对未知高程运动目标的跟踪、定位和测速，且性能优于传统EKF和IEKF算法。

2 时差频差测向融合跟踪模型

3星融合体制定位系统由1颗主星和2颗辅星构成，具体形式如图1所示，其中，α为地球自转时间角，f为真近心角(真近点角)，Ω为升交点赤经，w为近地点幅角，i为轨道倾角。系统的主星可通过干涉仪测得目标辐射源到达主星的方位角信息(Direction Of Arrival,DOA)，并可以测得辐射源信号到达该卫星与两个辅星的到达时间差(Time Difference Of Arrival,TDOA)与到达频率差(Frequency Difference Of Arrival,FDOA)信息。

图1 TDOA-FDOA-DOA跟踪定位系统示意图

设置卫星轨道为圆轨道，定义星体坐标系原点为卫星质心，X轴指向卫星前进方向，Z轴指向地球质心，Y轴与另外两轴成右手关系。为简化讨论，假设卫星姿态角为0，天线阵面安装角也为0，即主星的天线阵面坐标系与定义的主星星体坐标系重合。

卫星定位中，描述辐射源坐标时常采用WGS-84系(ECEF坐标系)，但参数的测量却是在卫星的天线阵面上进行的，因此为方便分析，应通过坐标系转换将辐射源和两颗辅星的位置转换至主星的天线阵面坐标系下(本文中即主星星体坐标系)。ECEF系至主星的星体坐标系间转换方式为

其中，(xe,ye,ze)为辐射源或卫星在ECEF坐标系下的坐标，(xt,yt,zt)为其在主星的星体坐标系下的坐标，(xe0,ye0,ze0)为主星在ECEF坐标系下的坐标，而(xt0,yt0,zt0)为主星在其本体坐标系下的坐标(0,0,0)，因此可在计算中省略，R1为ECEF坐标系到ECI坐标系的转换矩阵，忽略对其影响较小的章动和岁差，可由仿真时刻儒勒日计算出地球自转时间角α得 到；R2为ECI坐标系到主星的星体坐标系的转换矩阵，由轨道根数f,Ω,w,i得到。由式(1)可知，星体坐标系至ECEF坐标系的转换关系为

设置辐射源为一高程未知的等高程匀速运动目标，在k时刻，其状态方程为

其待定的位置和速度分别为(xk,yk,zk)和(vxk,vyk,vzk)，则该时刻辐射源运动状态矢量Xk=[xk,yk,zk,vxk,vyk,vzk]T,A为状态转移矩阵，定义为

其中，Δt为采样周期，wk-1为相应的过程噪声，其对应协方差为Qk-1。

方程组式(7)前3式为测量方程，其中，c为光速，tn,k和fn,k分别表示辅星n在k时刻与主星的时差(TDOA)、频差(FDOA)观测量；θk为主星的1维干涉仪测得的k时刻到达角观测量，为简化讨论，这里假设该角为来波方向与ECEF系的X轴方向的夹角，eX与eY为主星的星体系坐标轴的单位矢量，eX=[1,0,0]T,eY=[0,1,0]T。在跟踪过程中，辐射源始终做等高程匀速运动，因此其速度和位置矢量应满足正交性，由此得出方程组第4式。dtk,dfk,dθk,dOk为相互独立的高斯白噪声，其中，dtk,dfk,dθk分别代表时差、频差和角度的观测误差，dOk为目标位置与速度的正交约束误差。

3 改进IEKF跟踪算法

3.1 滤波初值计算方法

工程上，扩展卡尔曼滤波器(EKF)是一种应用广泛的非线性滤波器，利用EKF对辐射源目标的位置和速度进行滤波跟踪是解决此类问题的常用方式，对于EKF而言，一个理想的滤波初值可以带来更小的截断误差和更快的收敛速度，初始状态选择不当会导致滤波器发散，因此滤波初值选取的优劣对滤波结果有着直接影响。由定位方程组式(7)可知，时差和角度观测方程与目标速度无关，不会由于运动目标速度引入误差。因此，在研究运动目标时，首先融合TDOA和DOA两种定位信息来得到滤波初值。

滤波初值的计算在主星的星体坐标系下进行，首先设主星星体坐标系下辐射源初始位置为ub,t=[xb,t,yb,t,zb,t]，3 颗卫星初始位置为sb,n=[xb,n,yb,n,zb,n]，其中n=0时表示主星初始位置，其在星体坐标系中的坐标为(0,0,0),n=1,2时分别表示两颗辅星初始位置。设主星与目标辐射源的距离为r0，辅星与目标辐射源的距离为rn,n=1,2，则有

在主星的星体系下，有如式(9)测量方程

其中，tn,0分别表示辅星n在初始时刻与主星的时差(TDOA)观测量；θ0为主星的1维干涉仪测得的初始时刻到达角观测量(来波方向与主星星体坐标系X轴夹角)，dt0,dθ0分别代表初始时刻时差和角度的观测误差。

由方程组式(9)中的第1式可得

联立定位方程组式(9)第2式与式(10)可得

其中，n=1或2，进而有

将式(12)和方程组式(9)第2式代入式(8)，可得到关于r0的一元二次方程

由式(13)解得r0的两个根，去除镜像模糊值后，将得到的解代入式(12)和定位方程组式(9)第2式，解出目标在主星星体系下的初始定位坐标，将该位置坐标由式(2)坐标转换至ECEF坐标系下，即得到滤波初值u0。对于协方差矩阵，分别对式(2)及定位方程组式(9)的两式求解全微分，可得到初始位置估计的协方差矩阵

其中，d iag为以相应元素为对角线元素的对角阵，σt表示时差的测量精度，σθ表示方位角的测量精度，矩阵M为

目标运动状态此时未知，故将初始速度置为0，可得滤波初始值为(,0,0,0)，初始协方差矩阵为

其中，vmax为目标速度可能达到的最大值。

3.2 基于融合定位体制的EKF算法

卡尔曼滤波是一种可以对线性系统状态进行最优估计的算法，但融合体制3星定位系统是一个非线性系统[13]，为解决这一问题，本文首先给出了融合定位系统的扩展卡尔曼滤波(Extended Kalman Filter,EKF)方法，其基本思想是将非线性系统线性化，对非线性函数的泰勒展开式进行1阶线性化截断，忽略其高阶项，从而将非线性问题转化为线性，然后进行卡尔曼滤波。

首先设系统状态方程和观测方程分别为

其中，A是状态转移矩阵，状态转换函数h指代k个时间采样点下状态量Xk与观测量Zk之间的函数关系，wk-1为过程噪声，Rk为测量噪声。

EKF过程如下：

目标状态预测

预测协方差矩阵

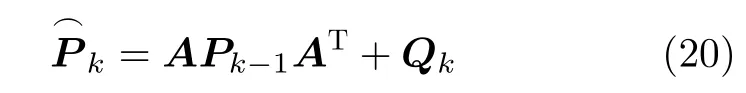
卡尔曼增益矩阵计算

更新目标状态

更新协方差矩阵

3.3 改进的迭代卡尔曼滤波(IEKF)算法

EKF算法应用在非线性系统时，会产生2次项以上的截断误差，尤其在线性模型误差较大时，可能导致滤波结果误差较大。IEKF算法在EKF的基础上，在测量更新阶段加入多次迭代，重复对观测方程进行线性化，最终得到更为准确的滤波结果，由文献[14]可定义其代价函数

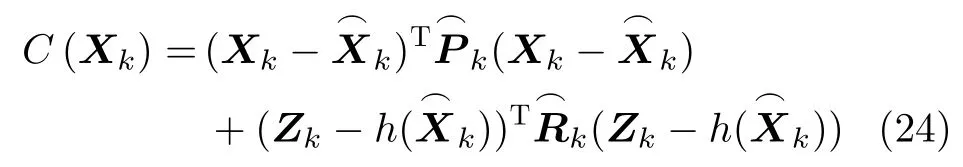
IEKF的迭代过程可视为利用高斯-牛顿方法迭代求解式(24)的极小值点，但由于线性化带来的截断误差等因素，往往只能求出其非零极值点，即等价于将高斯-牛顿方法应用于小残差问题的迭代优化。对于此类问题，IEKF算法存在着不稳定性，主要表现为对状态的观测更新不能保障误差的一致减小，对协方差阵估计值比真实值偏低，进而影响对观测信息的有效利用。为解决这一问题，本文算法利用L-M方法调整预测协方差阵，以保证算法具有全局收敛性，算法核心是在每次迭代过程中使用阻尼因子μi对协方差预测矩阵进行修正，以修正后的协方差矩阵进行观测的迭代更新[15–17]。具体过程如下：

目标状态预测

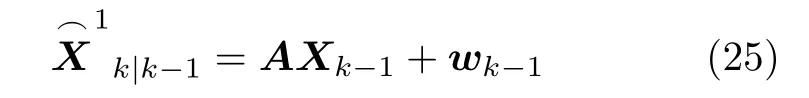
预测协方差矩阵

迭代开始

L-M方法修正协方差矩阵

卡尔曼增益矩阵计算

更新目标状态

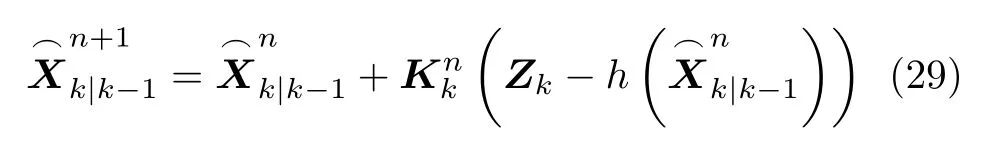
更新协方差矩阵

当代价函数随迭代次数增加而小于一定限度时，即认为收敛已至极值点附近，迭代终止条件可写为

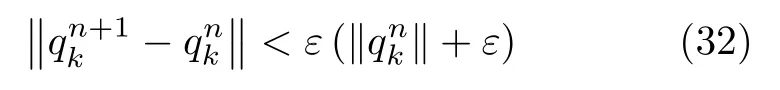
其中，ε是预先设置的门限值。

整个过程的具体流程图如图2所示。

图2 改进IEKF流程示意图

4 仿真结果与分析

利用融合定位体制对辐射源进行定位时，卫星的编队方式将对定位结果产生影响[18]，设3颗卫星轨道高度均为800 km，星间距100 km；目标初始位置为(28.73°E,8.61°N)，高程为10 km，目标运动状态方程如式(5)所示，做速度为400 m/s匀速直线运动。观测时长为100 s，观测时间间隔为1 s，时差测量误差为20 ns，多普勒频率测量误差为3 Hz，测向误差为0.25°。图3、图4分别给出了3星同轨和2星同轨1星异轨时的融合定位体制的GDOP图，图中的误差单位均为km。由图中可见在融合定位体制中，同轨3星的定位误差情况优于2星同轨1星异轨情况，这是由于本算法的主要误差来自测角误差，而3星同轨的编队方式在主星星体系下联立时差方程求解辐射源位置时所受测角误差影响相对三角构型要小得多，因此虽然对于时差测量来说等腰三角构型的误差情况要优于同轨3星构型[19]，但综合考虑总体误差，3星同轨编队方式依然更优。

图3 3星同轨GDOP分布

图4 2星同轨1星异轨GDOP分布

综合考虑卫星传感器的测量参数误差和覆盖范围情况，本文的算法更适合3星同轨编队的应用场景。图5—图8仿真分析了3星TDOA/FDOA系统的EKF跟踪方法、3星TDOA/DOA系统的EKF跟踪方法以及本文的融合跟踪系统EKF方法对于未知高程的运动目标位置、速度的跟踪性能，并将融合跟踪系统的EKF方法与改进IEKF方法进行了比较。

图5 目标定位跟踪结果

图6 目标高程跟踪结果

图7 目标位置估计误差

图8 目标速度估计误差

从图5、图6可以看出，在未知高程的情况下，本文所提融合定位算法可以实现运动辐射源目标的跟踪定位。从图7可以看出，本文融合定位系统的定位精度优于3星TDOA/DOA定位系统，且改进IEKF的融合跟踪方法定位精度略高于EKF算法。而由于对目标高程估计误差大，3星TDOA/FDOA定位性能明显不如其他算法，且其误差会随着目标高程增加而变得更大，4种算法收敛速度都较为缓慢，这是时差或频差的测量方程相对于目标位置的强非线性所导致的，在跟踪时加入迭代能一定程度上缓解这一问题。由图8可以看出，由于缺乏对速度参数的直接观测，3星TDOA/DOA定位系统对于速度的跟踪误差较大，而加入FDOA观测量后，对速度的跟踪性能明显提升。而由于定位初值偏差较大，3星TDOA/FDOA定位系统收敛速度明显不如本文提出的融合定位系统。

5 结束语

本文针对未知高程的运动目标跟踪问题提出了一种基于3星TDOA/FDOA/DOA的融合定位方法，并针对传统EKF方法定位跟踪精度低、收敛慢的问题，提出了改进的IEKF融合跟踪方法。首先利用3星时差信息和主星1维测向信息得到滤波初值及其协方差阵，再利用改进的IEKF结合3星频差信息进行滤波跟踪。仿真结果表明，在未知高程信息的情况下，算法可以实现运动目标的高精度位置跟踪，并能获得目标的高精度速度估计。