基于协方差矩阵重构的离网格DOA估计方法

王洪雁 于若男 潘 勉 汪祖民*

①(浙江理工大学信息学院 杭州 310018)

②(大连大学信息工程学院 大连 116622)

③(五邑大学智能制造学部 江门 529020)

④(杭州电子科技大学电子信息学院 杭州 310018)

1 引言

作为阵列信号处理领域研究热点之一，波达方向角(Direction Of Arrival,DOA)估计技术在无线通信、目标跟踪、语音处理、雷达和射电天文学等领域皆有广泛应用[1,2]。随着DOA估计理论研究的不断深入，各种DOA估计方法相继被提出。经典的子空间类方法可实现超分辨测向，例如多重信号分类(MUltiple SIgnal Classification,MUSIC)[3]、旋转不变子空间(Estimation of Signal Parameters via Rotational Invariance Technique,ESPRIT)[4]等，然而在低信噪比条件下，其估计性能将显著下降[5]。针对此问题，文献[6]提出一种最大似然(Maximum Likelihood,ML)DOA估计算法，其通过逐步迭代求解信号和噪声的对数似然函数以实现DOA估计，低信噪比条件下，其性能明显优于MUSIC算法，但其非常依赖初始值的选取且算法复杂度较高，从而限制了该算法的实际应用。因此，如何改善DOA估计算法性能同时降低计算复杂度是当前阵列信号处理领域的研究热点之一。

近年来，稀疏信号表示[7,8]和压缩感知[9,10]理论已逐步成为参数估计领域的有力工具。随着稀疏重构算法研究的不断深入，研究者相继提出众多基于信号空域稀疏特性的DOA估计方法，其中最具代表性的L1-SVD[11]算法，其利用L1范数构建稀疏模型而后通过奇异值分解降低计算复杂度。文献[12]提出一种基于加权L1范数稀疏重构DOA估计算法，其利用信号稀疏性并基于改进Capon算法的倒谱函数设计权值并构造加权L1范数凸优化问题以实现信源数目未知场景下DOA估计。文献[13]提出一种基于稀疏贝叶斯推理(Sparse Bayesian Inference,SBI)的互质阵列DOA估计算法，其利用线性变换从协方差向量中消除噪声方差，而后联合参数字典学习和稀疏恢复迭代更新以实现DOA估计。文献[14]提出一种基于低秩恢复的稳健DOA估计方法，其利用采样协方差矩阵稀疏及低秩特性构造关于信号和噪声协方差矩阵的凸问题，而后利用MVDR方法实现DOA估计。需要注意的是，上述DOA估计算法皆假设信源DOA精确位于预设离散网格点上，然而，信号实际到达角度可能与预设离散网格存在偏移，由此，所得估计存在一定误差[10]。针对此问题，最直观的解决方法是减小网格间距离，即利用较小步长即更密集搜索网格覆盖探测空间以降低估计误差，然而，此方法会显著增加计算复杂度且增加超完备字典原子之间相干性从而违背有限等距性质(Restricted Isometry Property,RIP)进而导致估计误差增大。针对上述问题，文献[15]提出基于稀疏贝叶斯学习的离网格(Off-Grid Sparse Bayesian Learning,OGSBL)DOA估计算法，通过引入偏移量参数至DOA稀疏表示模型并基于SBL求解，从而解决网格划分问题。文献[16]提出根稀疏离网格贝叶斯推理(Root Off-Grid SBI,ROGSBI)方法，采用粗分网格与迭代细分网格相结合优化网格以实现高精度DOA估计。需要注意的是，上述算法虽然基于SBI降低离网格效应并降低计算量，然而，其皆没有考虑有限次快拍可导致采样信号协方差矩阵存在估计误差[17]，进而使得上述算法所得DOA估计精度提升有限。

针对上述问题，本文提出一种网格失配条件下基于协方差矩阵重构的离散网格DOA估计方法(Off-Grid based on Covariance Matrix Reconstruction,OGCMR)。首先，将DOA与网格点之间偏移量包含进接收数据稀疏表示模型；而后基于重构信号协方差矩阵建立关于DOA估计的稀疏表示模型；接着，构建采样协方差矩阵估计误差凸模型，并基于采样协方差矩阵估计误差服从渐进正态分布的统计特性推导估计误差上界，而后将此凸集显式包含进稀疏模型以改善稀疏信号重构性能进而提升DOA估计精度；最后采用交替迭代方法求解所得联合优化问题以获得稀疏DOA和网格偏移参数估计。仿真实验验证了所提算法的有效性。

2 阵列信号模型

假设K个远场窄带信号入射至阵元数为M的均匀线性阵列，则t时刻接收信号模型可表示为

其中，x(t)为接收数据，a(θk)=[1,e-j2πdsinθk/λ,...,e-j(M-1)2πdsinθk/λ]T和sk(t)分别为第k个信号源的导向矢量和信号幅度，d和λ分别为阵元间距及载波波长，通常d ≤λ/2,{θ1,θ2,...,θK}为K个信源DOA(本文只考虑方位角，所得结论亦可推广至2维DOA估计)，A(θ)=[a(θ1),a(θ2),...,a(θK)]∈CM×K为阵列导向矢量矩阵，s(t)=[s1(t),s2(t),...,sK(t)]T∈CK×1为波形矢量，n(t)=[n1(t),n2(t),...,nM(t)]T为互不相关高斯白噪声。

对于L次快拍，式(1)接收信号模型可进一步表示为

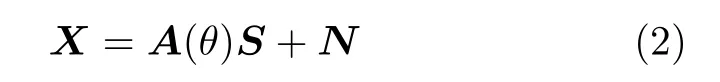
其中，X=[x(1),x(2),...,x(L)]为接收信号矩阵，S=[s(1),s(2),...,s(L)]为信号幅度矩阵，N=[n(1),n(2),...,n(L)]为噪声矩阵。

假设信号和噪声互不相关，且信源相互独立[18]，则接收信号协方差可表示为

其中，Rs为无噪声信号协方差矩阵，为信号功率协方差矩阵，σ2为噪声功率。

实际应用中，接收协方差矩阵R基于L次有限采样快拍估计得到[13]，即

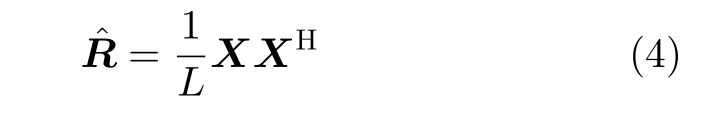
3 离网格DOA估计模型

由式(5)、式(9)可知，离网格DOA估计模型可表示为

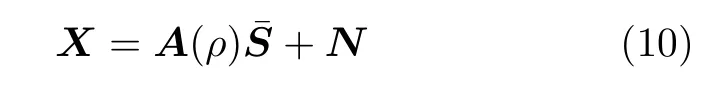
4 基于离网格的稀疏重构算法

基于上述讨论，协方差矩阵R可稀疏表示为

然而实际应用中由于采样次数有限，信号协方差矩阵存在估计误差，因而基于此稀疏表示DOA亦存在估计误差，进而导致DOA估计性能下降。针对此问题，类似于文献[18]，本文构建关于R的误差模型如下

其中，‖·‖F为矩阵Frobenius范数，ε为误差参数因子。

基于误差凸集，稀疏信号重构问题可基于l1范数约束最优化算法求解，即

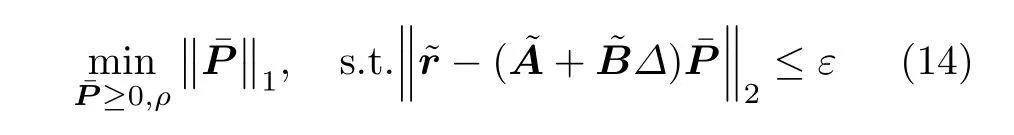
需要注意的是，求解上述优化问题需要误差上界ε确知。然而，此值在实际中难以确知，通常基于经验确定。基于此，本文基于协方差估计误差服从渐进正态分布的统计特性，推导误差上界的确定方法。由文献[20]分析可知，矢量化协方差矩阵误差服从渐进正态(Asymptotically Normal,AsN)分布，即

其中，χ2(·)表示卡方分布，A sχ2(M2)表示自由度为M2的渐进卡方分布。

由于向量r为协方差矩阵R的矢量化形式，从而可得

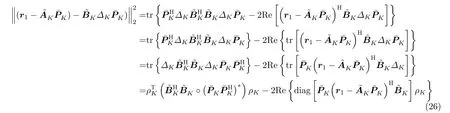
其中，Re 表示取实部，°表示矩阵的Hadamard积。

令式(26)关于ρ的导数为零，进而可得ρK的更新公式

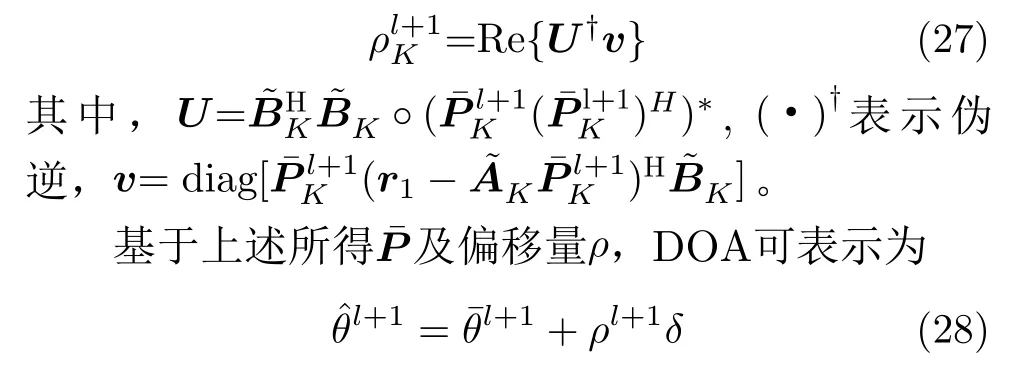
其中，δ为网格划分间隔。

综上所述，本文所提OGCMR算法可表述为

(1)输入阵列接收信号矩阵X；

(2)划分网格并引入偏移量ρ得到阵列流型矩阵A(ρ)；

(3)求解式(21)以获得误差参数η的最优估计值；

(5)求解式(27)更新ρ；

(6)求解式(28)获得DOA估计；

(7)重复步骤(4)—步骤(6)，直至相邻两次DOA估计值无明显变化，即。

5 实验仿真及分析

本节通过与传统MUSIC,L1-SVD及SLRDRMVDR算法在估计精度、角度分辨力、运行时间以及误差参数因子对DOA估计影响等方面的对比，验证所提OGCMR算法有效性。实验环境如下：仿真软件为MATLAB R2014a，硬件环境为：Intel Core(TM)i7-7700，主频4 GHz，内存8 GB。仿真条件为：阵元数M=8，快拍数L=200，阵元间距d=λ/2。其中，DOA估计精度可采用均方根误差(Root-Mean-Square Error,RMSE)衡量[24]，定义为

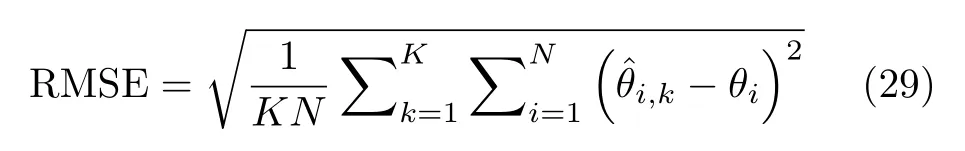
其中，K为蒙特卡罗试验次数，N为目标个数，为第k次实验对第i个 DOA估计，θi为第i个真实DOA。

5.1 空域谱对比

图1为4种条件下MUSIC,L1-SVD,SLRD-RMVDR和所提OGCMR算法的空域功率谱对比图。仿真条件设置如下：考虑两个入射角度分别为[–10.6°,5.3°]的非相干信号，由图1(a)可知，在信噪比SNR=0 dB，快拍数L=40的条件下，MUSIC可近似分辨出目标信号角度但其在–10.6°处谱峰较低，L1-SVD和SLRD-RMVDR算法均无法有效分辨目标信号，而本文所提OGCMR算法可有效辨别两个目标信号角度且具有较窄主瓣。由图1(b)可知，随着SNR增加，SLRD-RMVDR算法角度分辨力有所提高，而L1-SVD算法仅能近似分辨位于–10.6°的目标信号，且本文所提OGCMR算法依然具有较好的角度分辨力。图1(c)为SNR=0,L=200条件下4种算法空间谱估计对比图。由图1(c)可知，低SNR条件下，MUSIC算法在5.3°位置谱峰值较低，SLRD-RMVDR算法在–10.6°处谱峰值较低，L1-SVD算法无法有效分辨目标信号，本文所提OGCMR算法具有较好估计性能。图1(d)为SNR=10 dB,L=200条件下4种算法的空间谱估计对比图。由图1(d)可知，随着SNR和快拍数的增大，4种算法皆具有较为尖锐的谱峰，且所提算法具有更窄主瓣，更为接近真实的DOA，因而具有更优的DOA估计性能。

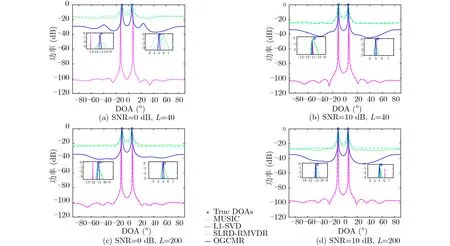
图1 不同信噪比和快拍条件下非相干信号空域谱对比图

图2为4种算法空域谱估计对比图。仿真条件设置如下：考虑4个入射角度分别为[–35.3°,–10.6°,5.3°,26.5°]的非相干信号，SNR=10 dB，快拍数L=200。由图2可知，给定仿真条件下，MUSIC,L1-SVD和SLRD-RMVDR 3种算法所估计的角度与实际目标信号角度均存在一定偏差，而本文所提OGCMR算法可有效分辨4个目标角度，并且相较于MUSIC和l1-SVD两种对比算法具有较窄主瓣及较低旁瓣，这是因为所提OGCMR算法将DOA与网格点之间偏移量包含进接收数据稀疏表示模型，并构建采样协方差矩阵估计误差的凸模型，且将此凸集显式包含进凸稀疏表示模型以改善稀疏信号重构性能，进而实现有效DOA估计。

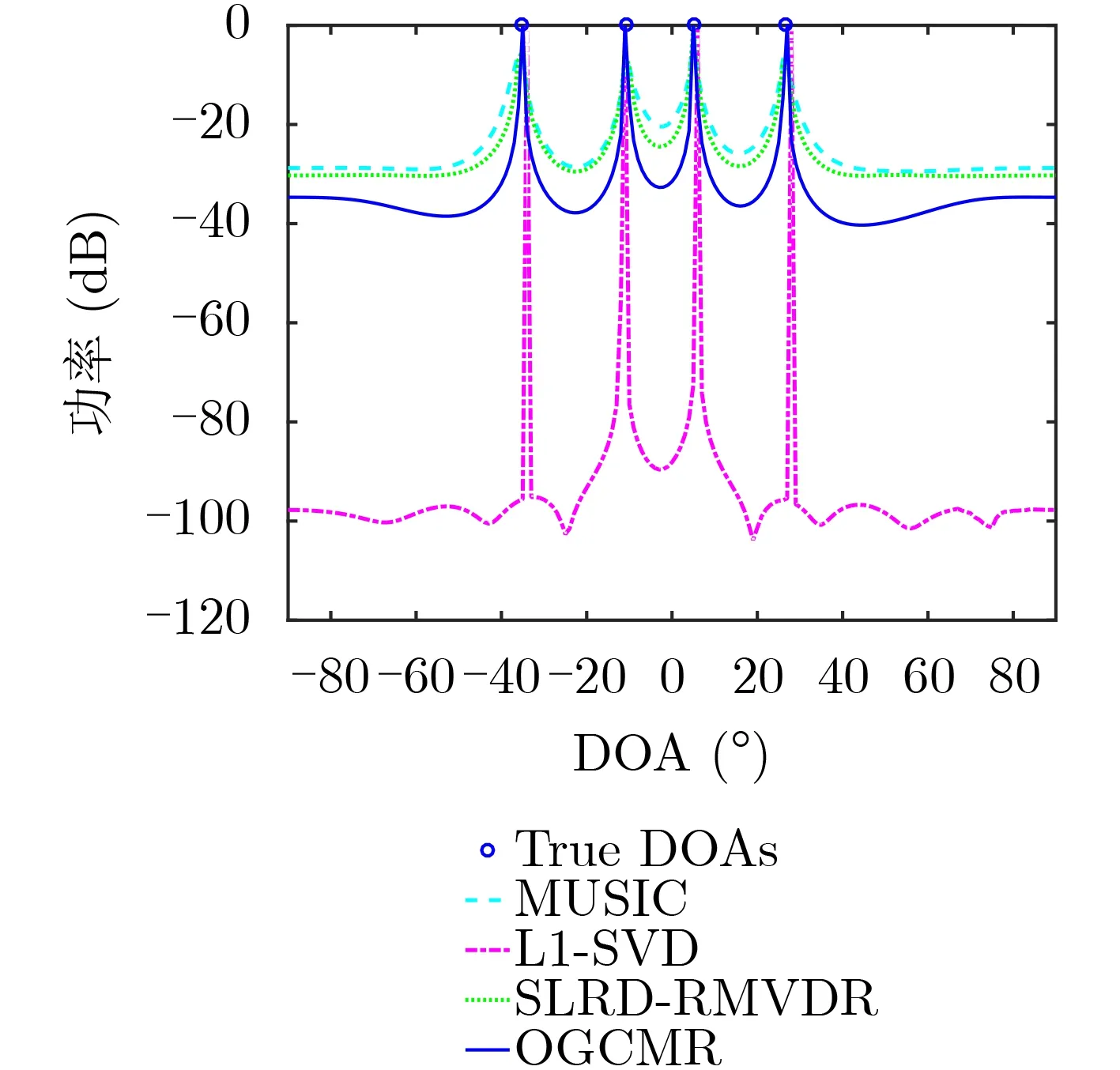
图2 非相干信号空域谱

5.2 DOA估计RMSE

图3为4种算法DOA估计RMSE随SNR变化曲线。仿真条件设置如下：考虑入射角分别为–10.6°和5.3°的非相干信号，且SNR=[–6:2:14] dB，快拍数L=200，进行200次蒙特卡罗独立重复实验。由图3可知，随着SNR增加，4种算法DOA估计RMSE均逐渐降低。需要注意的是，传统MUSIC和L1-SVD算法的DOA估计RMSE相对较高，SLRDRMVDR和所提OGCMR算法的RMSE较低，且所提算法估计性能明显优于SLRD-RMVDR，这是因为所提算法考虑到DOA与网格点之间存在偏移量并将其包含进接收数据稀疏表示模型，尤其在低SNR条件下，所提算法的优势更加突出，由此表明所提OGCMR算法具有较好的DOA估计性能。

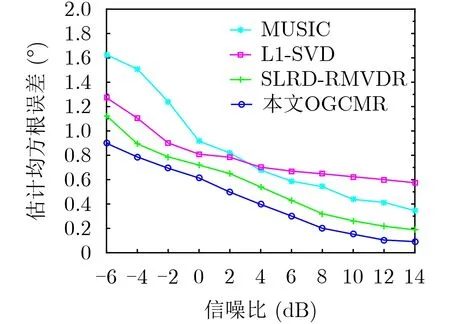
图3 DOA估计RMSE随SNR变化曲线

图4为4种算法DOA估计RMSE随快拍数变化曲线。仿真条件设置如下：考虑入射角分别为–10.6°和5.3°的非相干信号，SNR=10 dB，快拍数L=[50:50:500]，进行200次蒙特卡罗独立重复实验。由图4可知，随着快拍数增加，MUSIC,L1-SVD,SLRD-RMVDR和本文所提OGCMR算法的RMSE均逐渐降低。另外，需要注意的是，所提OGCMR算法因其考虑到DOA与网格点之间存在偏差以及采样协方差矩阵存在误差，并构建相关联合优化问题以改善稀疏信号重构性能，故而在相同快拍数条件下，所提算法具有优于其他3种算法的DOA估计性能。

图4 DOA估计RMSE随快拍数变化曲线

5.3 算法复杂度

为评估所提算法复杂度，在此分析不同快拍数条件下算法运算时间对比。

图5为4种算法运算时间随快拍数变化曲线。仿真条件设置如下：考虑两个入射角分别为–10.6°和5.3°的非相干信号，SNR=10 dB,L=[50:50:500]。由图5可知，随着快拍数增加，4种算法运算时间皆呈上升趋势。所提OGCMR和L1-SVD算法利用过完备字典矩阵稀疏重构信号，而SLRD-RMVDR基于低秩恢复理论重构无噪声协方差矩阵，此3种算法运算时间略高于传统MUSIC算法，且L1-SVD算法由于在未降维的数据上采用凸优化方法来重构信号，因而耗时较长。然而，需要说明的是，虽然所提OGCMR算法的运行时间略高于MUSIC 算法，但其DOA估计精度和角度分辨力明显优于MUSIC算法，即所提算法能以较小的时间为代价换取DOA估计性能的提升。

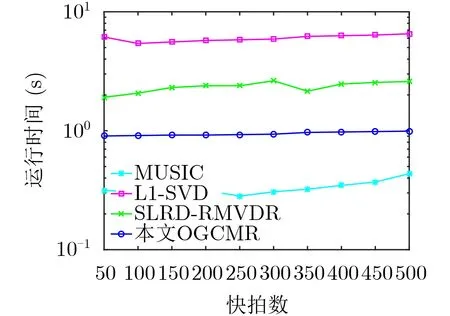
图5 算法运算时间随快拍数变化曲线

5.4 误差参数分析

为较全面地评估所提OGCMR算法性能，在此分析误差参数η对所提算法重构性能的影响。

表1为误差参数对所提OGCMR算法重构性能影响。仿真条件设置如下：考虑入射角分别为–10.6°和5.3°的非相干信号，SNR=10 dB，快拍数L=200。由表1可知，误差参数为0.1时，所提OGCMR算法重构信号峰值功率较大，随着误差参数的增大，所提算法重构信号的峰值功率逐渐降低，表明误差参数η取值对算法重构性能有较大影响。

表1 误差参数对算法重构性能影响

6 结束语

针对基于稀疏表示的DOA估计存在网格失配问题，即信源方位角可能不完全位于离散网格进而产生估计误差，本文提出一种基于重构协方差矩阵的离网格DOA估计(OGCMR)方法。所提算法首先将DOA与网格点之间偏移量包含进接收数据稀疏表示模型，而后构建采样协方差矩阵估计误差凸模型，并将此凸集显式包含进稀疏表示模型，最后采用交替迭代方法求解所得联合优化问题以获得稀疏DOA和网格偏移参数估计。与多重信号分类(MUSIC)、L1-SVD及基于稀疏和低秩恢复的稳健MVDR (SLRD-RMVDR)等DOA估计算法相比，仿真结果表明，所提算法在网格失配条件下具有较高的角度分辨力和DOA估计精度。