Effects of resonant magnetic perturbations on radial electric fields in DIII-D tokamak

Jingyuan FU (付敬原) , Pengfei LIU (刘鹏飞), Xishuo WEI (魏西硕),Zhihong LIN (林志宏), Nathaniel Mandrachia FERRARO and Raffi NAZIKIAN

1 Fusion Simulation Center, Peking University, Beijing 100871, People’s Republic of China

2 Department of Physics and Astronomy, University of California, Irvine, CA 92697, United States of America

3 Princeton Plasma Physics Laboratory, Princeton, NJ 08543, United States of America

Abstract Gyrokinetic simulations of DIII-D tokamak equilibrium find that resonant magnetic perturbation(RMP)drives a neoclassical non-ambipolar electron particle flux,which causes a rapid change of equilibrium radial electric fields consistent with experimental observations during the suppression of the edge localized mode(ELM).The simulation results provide a support for the conjecture that RMP-induced changes of radial electric fields lead to the enhanced turbulent transport at the pedestal top during the ELM suppression(Taimourzadeh et al 2019 Nucl.Fusion 59 046005).Furthermore,gyrokinetic simulations of collisionless damping of zonal flows show that resonant responses to the RMP decrease the residual level of the zonal flows and damp the geodesic acoustic mode.

Keywords: resonant magnetic perturbation, neoclassical transport, zonal flow, electric field

1.Introduction

In tokamak high-confinement regime (H-mode) with an edge transport barrier, edge localized modes (ELM) [1] are often observed to drive a large energy flux from the pedestal region to plasma-facing components [2].The resonant magnetic perturbations (RMP), produced by a set of external coils, have been showed to be effective for ELM suppression/mitigation [3–8].The mode stability analysis [3, 4] shows that the RMP can stabilize the ELM by enhancing the radial particle transport at the pedestal top,thus preventing the pedestal from reaching the stability boundary.However, the mechanism for the enhanced particle transport at the pedestal top,i.e.density pump-out is not well understood[5,9].Meanwhile,a rapid damping of toroidal flows at the pedestal top [10] is often observed during the transition from ELMing to ELM suppression state.This flow damping plays an important role in the turbulent transport that causes the density pump-out at the pedestal top in a DIII-D shot[11].The flow damping is mostly caused by a rapid change of equilibrium radial electric fields since plasma pressure profiles change much more slowly during the transition to the ELM suppression.An outstanding issue is that how the 3D RMP causes the rapid change of the equilibrium radial electric fields.

The short timescale of the rapid flow damping implies that the magnetohydrodynamic (MHD) braking effect [12]does not make the dominant contribution.Beyond the MHD theory,several kinetic theories have been proposed to explain the toroidal torque induced by the 3D RMP.In particular,neoclassical toroidal viscosity(NTV)theory[13–15]suggests that the 3D RMP can induce a radial transport of trapped particles, which generates a toroidal braking torque.Qualitative agreement has been obtained[16–20]between the NTV theory and the braking torque measured in the experiments,but a quantitative discrepancy persists.More importantly,prediction of the particle pump-out associated with the enhanced particle fluxes requires self-consistent calculation of the ambipolar electric fields,which have not been considered in the NTV theory [21].

Recently, gyrokinetic simulations have made impressive progress studying neoclassical and turbulence transport in tokamak with 3D RMP.Gyrokinetic RMP simulations initially used vacuum magnetic field generated by the I-coil without plasma responses [22–25].A gyrokinetic quasilinear theory [26] predicts an enhanced transport in the pedestal region due to the reduction of the RMP shielding by the reversal of the equilibrium radial electric field on a resonant surface.However, the plasma responses greatly affect the RMP penetration and magnetic island formation [27], which need to be taken into account in the gyrokinetic simulations of neoclassical and turbulent transport.Indeed,gyrokinetic GTC[28] simulations of a DIII-D tokamak equilibrium with plasma non-resonant responses to the RMP find that the 3D equilibrium with closed flux-surfaces does not enhance turbulence transport since the RMP amplitude is too small to have significant effects on linear drift-wave instability or zonal flow damping [29].Further GTC simulations find that the reduction of the radial electric field shear at the top of the pedestal during ELM suppression leads to enhanced microturbulence and extended turbulence spreading to the top of the pedestal relative to ELMing plasmas with similar RMP and pedestal parameters (see figures 5–8 of [11]).

Subsequently,gyrokinetic XGC simulations use the DIIID equilibrium with both resonant and non-resonant responses to the RMP to study the neoclassical transport in a short time scale before the ELM suppression, and show that non-ambipolar neoclassical transport can cause a rapid change of radial electric fieldsErnear the magnetic separatrix [30], which leads to the enhanced turbulent transport [31] in agreement with the earlier GTC results[11].However,the mechanism of the fastErchange(i.e.the driving term)has not been carefully studied in a long time range from the ELMing to ELM suppression state, and the simulation results of theErchange have not been compared with experimental value carefully.Furthermore,the stochastic region near the separatrix plays an important role in references [30, 31], while the focus of this paper is on the pedestal top and there is no global stochasticity from the pedestal top to the separatrix.We point out that the fast electron flux along the stochastic field line is mostly heat flux (i.e.Rechester–Rosenbluth theory [32]), but the RMP induces the density pump-out while temperature profile changes little.

In this work,we use GTC simulations to study the RMP effects on the radial electric fields including both equilibrium electric fields associated with toroidal rotations and zonal flows generated by microturbulence, which greatly affect the turbulent transport in tokamaks.Several theories have studied the effects of the RMP on the zonal flow damping [33–35].However,the validity of these theories should be verified with the gyrokinetic simulations.GTC simulations of the microturbulence and neoclassical transport in 3D toroidal geometry including stellarators [36, 37] and tokamaks with 3D magnetic fields [11, 29, 38–41] have been extensively verified.GTC simulations reported in this paper use realistic DIII-D tokamak equilibrium with both resonant and non-resonant responses to the 3D RMP calculated by the resistive MHD code M3D-C1[42].Neoclassical simulation results show that RMP-induced magnetic islands and stochastic electron orbits drive a non-ambipolar electron particle flux,which leads to a rapid change of equilibrium radial electric fields consistent with experimental observations during the transition from the ELMing to ELM suppression state.The GTC neoclassical simulation results on the pedestal top are in qualitative agreement with the XGC neoclassical simulation results near the magnetic separatrix [30] and provide a support for the conjecture that RMP-induced changes of radial electric fields lead to enhanced turbulent transport at the pedestal top during the ELM suppression[11,31].Furthermore,GTC simulations of collisionless damping of zonal flows find that resonant responses to the RMP decrease the residual level and damp the geodesic acoustic mode (GAM).

The rest of the paper is organized as follows.GTC neoclassical simulation model for the tokamak equilibrium with the 3D RMP is formulated in section 2.Simulations of neoclassical transport with the RMP without and with equilibrium electric field are presented in sections 3 and 4,respectively.In section 5,we calculate the time rate of change of the equilibrium radial electric field due to the non-ambipolar electron particle fluxes.Effects of the 3D RMP on the collisionless damping of zonal flows are discussed in section 6.Finally, conclusions and discussions are discussed in section 7.

2.Formulation of neoclassical simulation in tokamak with 3D RMP

2.1.Implementation of tokamak equilibrium with 3D RMP in GTC

In this work,GTC simulations use magnetic equilibrium with full plasma response to RMP, including both non-resonant response (which preserves closed flux surfaces) and resonant response (which creates magnetic islands and/or magnetic stochasticity)calculated by the resistive MHD code M3D-C1[42].The equilibrium profiles [10, 11, 29] from the DIII-D discharge#158103 at 3050 ms,when ELM is suppressed by then=2 RMP, are chosen as the base case for GTC simulations.

The equilibrium magnetic field can be written as B=B0+δB, where B0represents the equilibrium magnetic field of an axisymmetric tokamak and δB represents the 3D RMP.In GTC, the Boozer coordinate(ψ,θ,ζ)is used,corresponding to poloidal magnetic flux, poloidal and toroidal angles.The equilibrium magnetic field can then be represe=riant form:B0=δ∇ψ+g∇ζ+I∇θ=q∇ψ× ∇θ+∇ζ× ∇ψ.Here,qis the safety factor,2πgand2πIare poloidal and toroidal currents,and δ represents the components of the currents that depend on the poloidal angle.The perturbed magnetic field is cast in GTC using a reduced formδB= ∇×(αB0),which preserves the radial component of perturbed field.The M3D-C1 provides the Fourier serieswhereαmnis the coeffciient of the Fourier series.The function α calculated by this Fourier series is then converted to a 3D spline function in GTC [29, 43].

Figure 1(a) shows the Poincare plot of the equilibrium magnetic field with the 3D RMP at theζ= 0 poloidal plane,whereψis normalized with its valueψwat the last closed flux surface.In the region betweenψ= (0.87– 0.97)ψw,three island chains(m/n)= ( −7/ 2 ), (− 8/ 2 ), ( − 9 /2) are clearly separated by Kolmogorov–Arnold–Moser surfaces.The Chirikov parameter (defined in equation (2)in[44])at =q4 rational flux surface is 0.33.While there is very little stochasticity of the magnetic field lines, the particle orbits may still possess some stochasticity due to the cross-field guiding center drifts that sample multiple magnetic islands.The island widths in the high field side are,respectively,0.5,1.5 and 1 in the unit of local proton Larmor radius.Since the 8/2 island is the largest,we focus on the physics around the =q4 rational flux surface (ψψ= 0.93w).

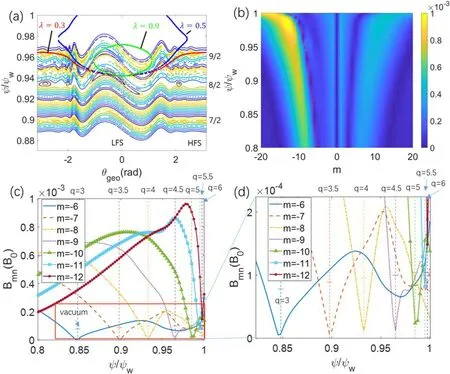
Figure 1.(a)Poincare plots on the ζ = 0 poloidal plane for magnetic field lines(small points),and deuterium gyrocenter orbits(red,blue and green big points) for three different pinch angles λ with local thermal speed.Here,θgeo(rad) is geometric poloidal angle.(b) Spectrum of n=2 RMP magnetic field as a function of poloidal harmonic m and poloidal fluxψ.Dashed red line represents resonant response.(c)Radial profiles of perturbed magnetic fields B mn ,where the red rectangular box is enlarged in panel (d).

Figure 1(a) also shows the Poincare plot for deuterium gyrocenter orbits around theψψ= 0.95wflux surface with three different pinch anglesλ≡=0.3,0.5 and 0.9,which correspond to the typical passing particle, barely trapped particle, and deeply trapped particle, respectively.The guiding center orbits in the region outside ofψψ= 0.95wcould be strongly affected by the magnetic separatrix of the divertor,which is then expected to play the dominant role in the ion neoclassical transport in the pedestal[30].Since the widths of the ion guiding center orbits are much larger than the RMP island width around the =q4 rational flux surface,the RMP islands should not affect the ion neoclassical transport significantly [30, 45] due to gyroaveraging and guiding center orbit averaging effects, especially when comparing with the dominant role of the magnetic separatrix in regulating the ion neoclassical transport.Therefore, we neglect the effect of RMP on the ion dynamics, and only study the single-species neoclassical transport of the electron in this work.

Figure 1(b)shows the poloidal spectrum of the perturbed magnetic fieldwhereAis the surface area of the magnetic flux surface andJis the Jacobi of the coordinates.The plasma response could be separated into the resonant response and non-resonant response.The resonant response could be quantified by the magnitude of the perturbed magnetic field at rational surfaces,represented by the red dashed line where/=q m n.The negativemof resonant responses indicates the left-handed helicity of the plasma currents.

Figure 1(c) shows the radial profiles of several poloidal harmonics of the RMP.The vertical dashed lines correspond to the radial positions of different rational surfaces.The horizontal short lines correspond to the vacuum RMP field values at the rational surfaces.Figure 1(d)shows the enlarged red rectangular region in figure 1(c), where the ratio between the resonant response and the vacuum RMP field value at theq=4 rational surface is about 0.1, which indicates that the RMP is strongly screened by the plasma response.

Figure 2.Axisymmetric equilibria of DIII-D discharge #158103 at 3050 ms.(a) Cross section between ψ= 0.984ψ w (solid line) andψ= 0.86ψ w (dashed line).(b) Electron density ne and temperature Te profiles, values onψ= 0.86ψ w are 2.4 ×101 3cm−3 and 1.45 keV.(c) Safety factor q and electron effective collision frequencyυ* profiles.

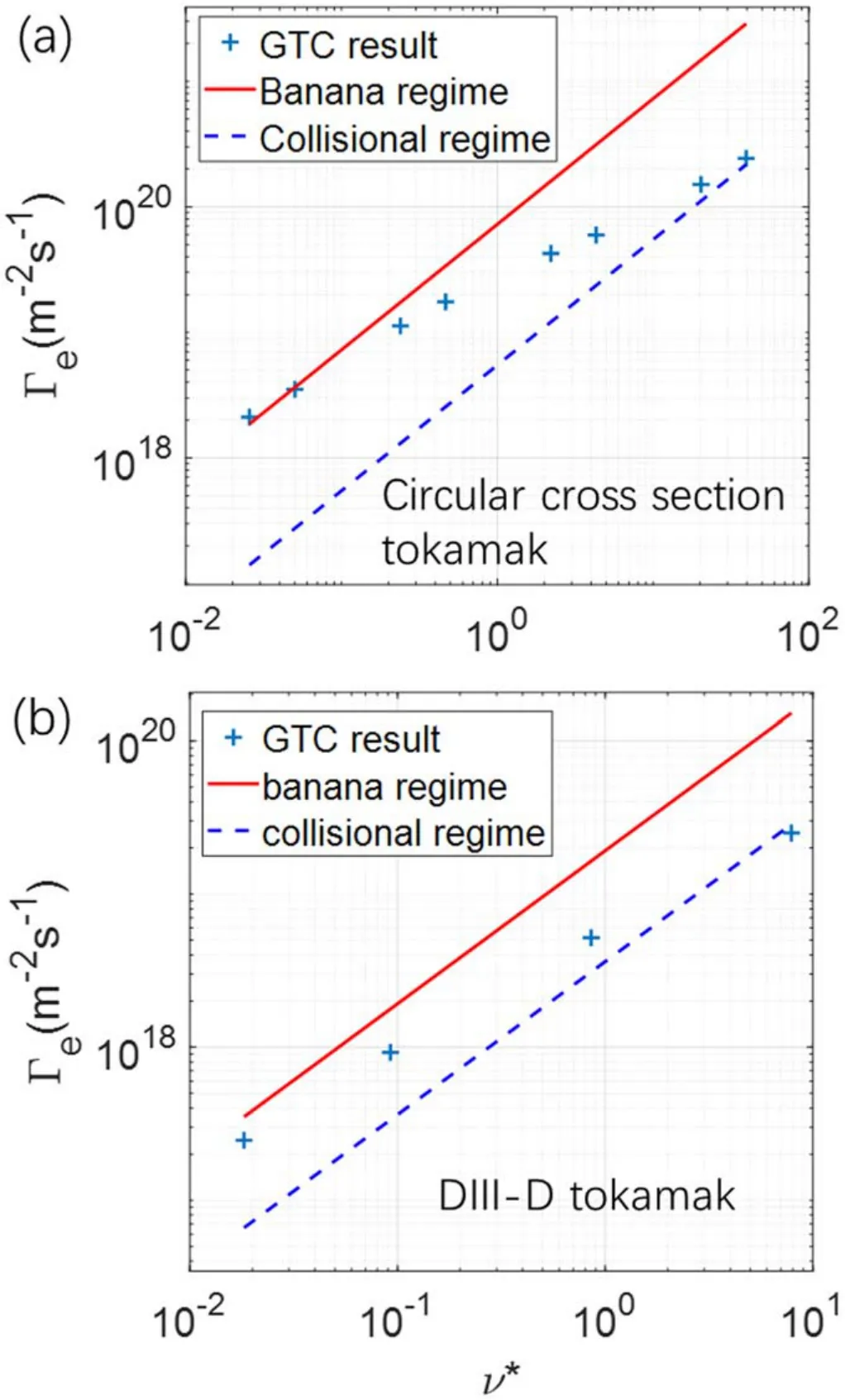
Figure 3.Neoclassical particle fluxΓe dependence on effective collision frequencyυ*without RMP and electric field under circular cross section tokamak (panel a) and DIII-D tokamak (panel b).The line is analytic expression in banana regime (red solid line) and collision regime (blue dashed line).

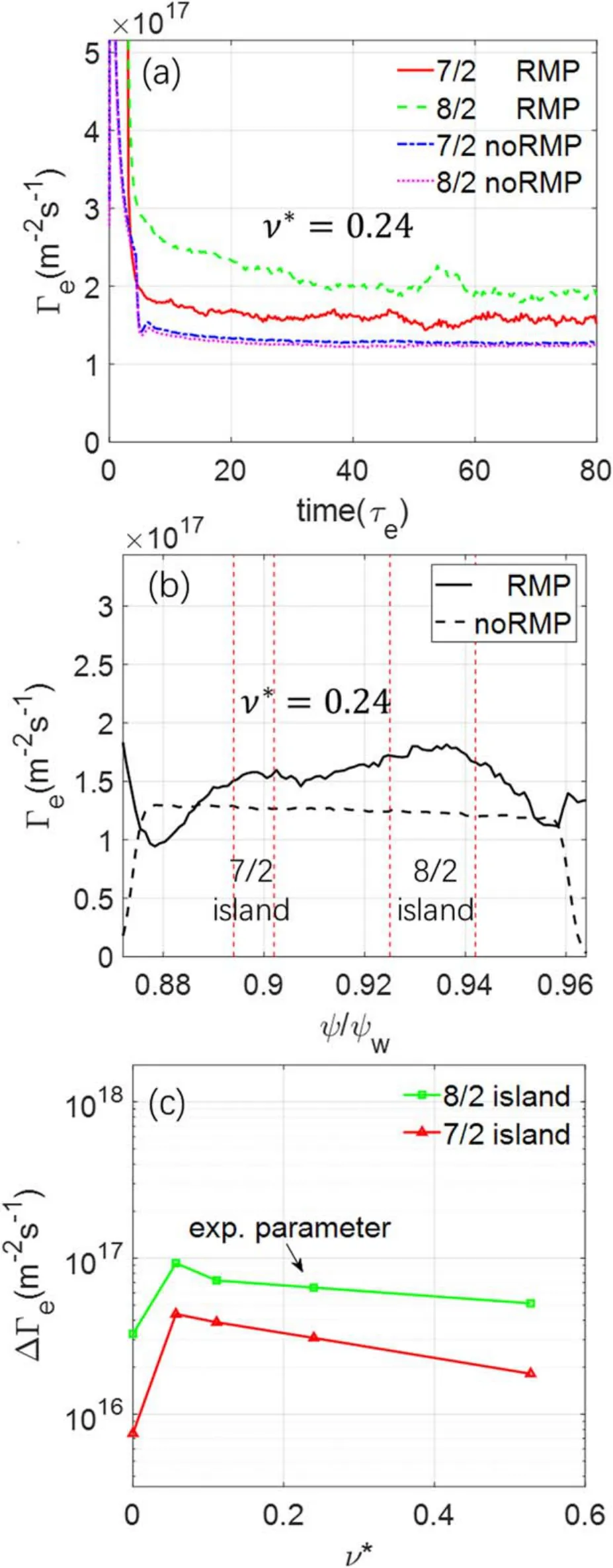
Figure 4.Neoclassical electron particle flux in rigid rotation case.(a)Time history ofΓe at 7/2 and 8/2 island regions in simulations with and without RMP.(b)Γe profile averaged over t =[40, 80] τe in simulations with and without RMP.Vertical dashed lines represent island separatrices.(c)Dependence of ΔΓe on collision frequencyυ*at 7/2 and 8/2 island regions.

2.2.GTC simulation model of neoclassical transport with RMP and radial electric field

In the GTC neoclassical simulations,the dynamics of electron gyrocenter are calculated by the Hamiltonian[46]in the phase space(X,E,μ),

where X is the spatial coordinates,Eis the particle kinetic energy,μ is the magnetic moment.meis the mass of electron,−eis the charge of electron,‖vis the parallel velocity along the field line,Bis the amplitude of magnetic field,andφis the electrostatic potential.

The drift kinetic equation describing the guiding center equations of motion based on this Hamiltonian with static magnetic perturbations takes the form

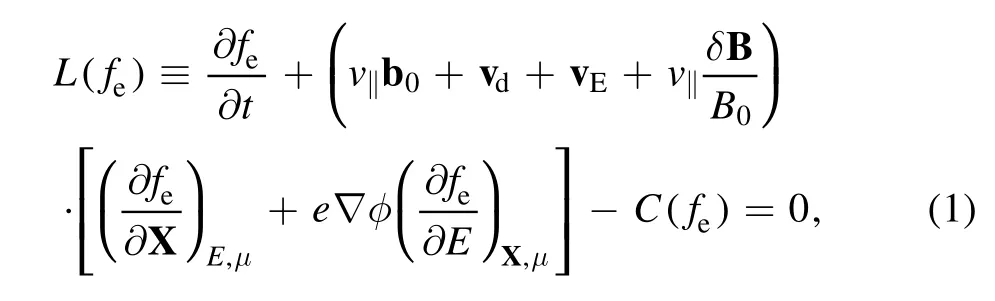
wherefeis the electron gyrocenter distribution function,Cdenotes the Fokker–Plank collision operators,which include inter-species and like-species collisions that conserve particle number, momentum and energy [47].The drift velocityvddenotes the magnetic curvature and gradient drifts,andvEdenotes the E×B drift.In the absence of magnetic perturbationsδB, the drift velocity could be written as:Here,cdenotes the speed of light,

In GTC, the perturbativeδfmethod is used in the simulation of neoclassical transport[47]to reduce the particle noise.The total distribution function could be separated into equilibrium and perturbation part:fe=f0e+δfe.We also expand theLinto two parts, that isL=L0+δL,and

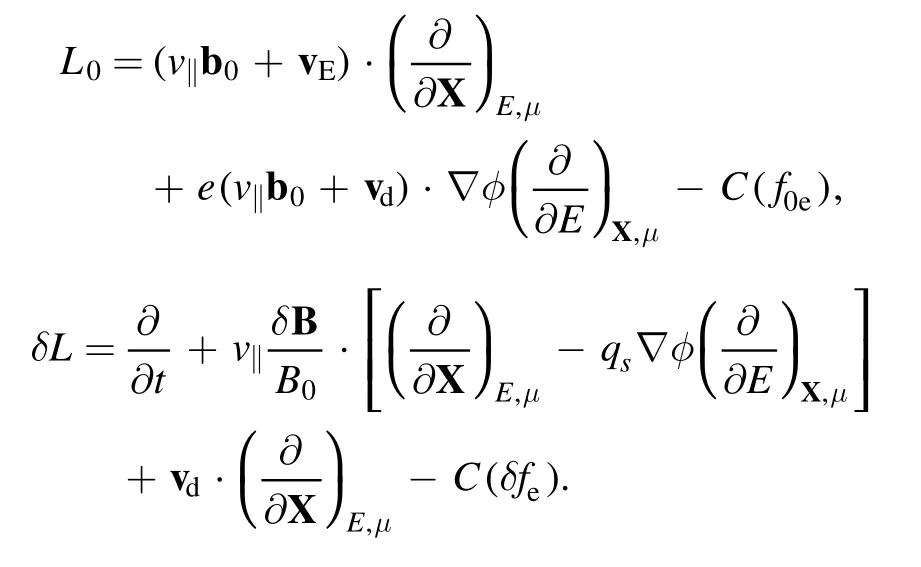
Here, we assume that the potential (φ)ψis only the function of flux surface.

The equilibrium distribution function is defined by

Since the collision operator inL0will relax the electron distribution function to the Maxwellian in the ion frame, the solution off0eis a shifted Maxwellian

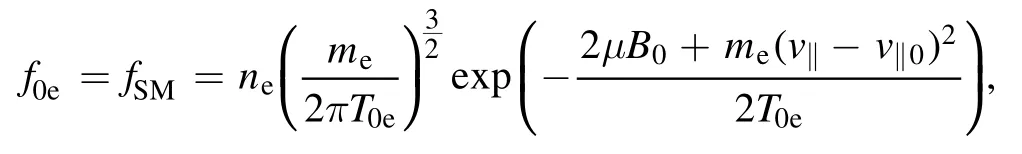
The perturbed distribution function obeys the following perturbed drift kinetic equation

Here,higher order terms inv‖0/v‖eare neglected and the equilibrium gradient parameter is defined as

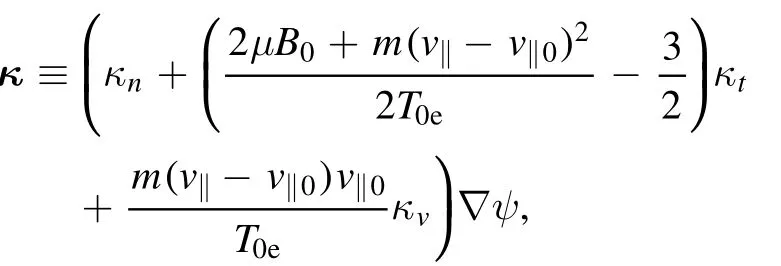
where

2.3.Verification of GTC simulation of neoclassical transport

In this subsection,we verify simulation results of neoclassical transport for both an axisymmetric circular cross section tokamak and the DIII-D tokamak.In the neoclassical simulation, uniform Maxwellian distributions of electron markers are loaded over an annulus of a tokamak.Based on convergent studies,a total of×4.23107particles are used in all the neoclassical simulations in this paper.Ions are treated as the cold, fixed background.

For the circular cross section tokamak, we use the representative parameters with a major radiusR0=1.86 m,a minor radiusa=0.246R0,the magnetic feild strength on axisB0=1.35 T,uniform electron temperature proflie withTe=5.0 keV,electric fliedEr=0,a safety factor proflieq=1.475 +a density profile=neAt =ra0.5 ,q =2,Zeff=1,and the gradient scale length value of density is R0/ Ln=2.2.The effective electron collision frequencyυ *=ε−3/2υqR0/vthis defnied as the physical collision frequencyυ normalized by the bounce frequency, where/ε = r R0is the local inverse aspect ratio,is the electron thermal velocity.

For the DIII-D tokamak, figure 2 shows the equilibrium cross section and profiles after the ELM suppression.The 2D plot of the simulation domain is shown in the figure 2(a).The equilibriumneand Teprofiles are plotted in figure 2(b), q profile andυ* profiles of electron are shown in figure 2(c),respectively.At the =q 4 rational surface, the gradient scale length value of density and electron temperature are R0/ Ln=9.2and R0/ LTe=18,υ *= 0.24,Zeff=3,and ε = 0.27 are evaluated on the outmost midplane.The equilibrium inhomogeneity scale length at =q 4 rational surface is larger than the poloidal ion Lamour radius, ρiθ/LTe=0.5,and is much larger than the island width W8,2/LTe=0.04.In this verification simulation,the knof electron and Teare set to be uniform by using the value at =q 4 rational surface(ψ= 0.935ψw),which is referred to as the rigid rotation case.Other important parameters are Er=0,R0=1.76 m,the magnetic field strength on axis B0=1.8 T.

The neoclassical particle fluxes in the absence of the RMP and electric field are simulated for various collision frequencies to verify the neoclassical simulation model.The relation between electron particle fluxΓeat steady state versus υ*is plotted in the figure 3,whereFor comparison,the analytic values ofΓein the banana regime and collisional regime are also plotted.For the circular cross section tokamak, the GTC neoclassical simulation results agree well with the analytic results for [47, 48] in both low and high frequency regimes.For the DIII-D tokamak, the simulation results are slightly smaller than the analytic results in both frequency regimes,presumably due to the shaping and finite aspect ratio effects neglected in the analytic theory.

3.Effects of RMP on neoclassical particle flux without equilibrium electric field

We now study effects of the RMP on electron particle fluxes Γeusing the equilibrium and plasma parameters of the DIII-D discharge #158103 as described in section 2.Since the main island chains at the =q 4 rational surface are close to the separatrix, high energy trapped ions can cross the separatrix into the scrape-off layer(SOL),as shown in figure 1(a).These lost ions can have significant effects on the radial electric fields near the separatrix even without applying RMP[30,31].The focus of this paper is to calculate the additional effects of the RMP, on top of the lost ions and the electrons.Therefore, we assume that ion and electron have already achieved ambipolarity before RMP is applied.Also, only the electrons are simulated, assuming that effects of the RMP on the ion transport is much smaller than the electron transport.

3.1.Verification of RMP effects with rigid rotation case

In this subsection, we use the rigid rotation case to verify the effects of the RMP on neoclassical transport, where the particle fluxes in the presence of the RMP are measured byDefine the non-ambipolar particle flux induced by the RMPΔΓe≡ΓRMP−Γ0,whereΓRMPandΓ0are the neoclassical electron particle fluxes with and without the RMP.The neoclassical particle flux in axisymmetric tokamak Γ0is intrinsically ambipolar[38, 40, 44].However,ΓRMPis not ambipolar andΔΓecan induce a change of ambipolar electric field to restore the ambipolarity, similar to the neoclassical transport in stellarators [37].

Figure 4(a) shows the time history of volume-averaged electron particle fluxesΓearound 8/2 and 7/2 island regions.The electron particle fluxes reach a steady state after a few collision timesτe= 1 /υ.In the simulation without the RMP,there is no obvious difference between theΓein these two regions.However,in the simulation with the RMP,compared with the 7/2 island, the wider 8/2 island induces a much larger increase of electron particle fluxΔΓeat steady statet=40τe.TheΔΓeinduced by the 8/2 island is comparable to theΓ0,but is much smaller than the turbulent transport level and therefore does not contribute to the density pump out.However, the non-ambipolar particle fluxes can induce an ambipolar electric field, which will be calculated in the section 5.

Figure 4(b) shows theΓeradial profiles averaged overt=[40, 80]τein the simulations with and without the RMP.Three regions,the 7/2 island region(q=3.44–3.55),the 8/2 island region (q=3.84–4.15), and the non-resonant region(q=3.55–3.84),are separated by the island separatrices.The larger 8/2 island induces a much largerΔΓethan those in the 7/2 island region and in the non-resonant region, which suggests that the non-ambipolar electron particle flux is mostly driven by the resonant component of the RMP.

Figure 4(c)shows theΔΓein the simulations varying the collision frequencyυ*= [0, 0.5]in the two island regions.TheΔΓein the collisionless case is much smaller than that in the simulations with collisions,which indicates that the flutter transport due to magnetic stochasticity is not dominant [32].TheΔΓein both the 7/2 and 8/2 island regions slightly decreases with the collision frequency in the banana regime.

Figure 5(a) shows the relaxation of electron density profiles in the 8/2 island region in the collisionless simulations with and without the RMP.On the high field side, the electron density profile is locally flattened inside the 8/2 island region and reaches the steady state after some bounce times.On the low field side,the electron density profile is less affected by the RMP,because the trapped particles on the low field side do not follow the field line around the magnetic island.In the collisional simulations, the collisions could further modify the density profiles [39].

Figure 5(b)shows the relaxation of electron diamagnetic frequencyprofiles in the 8/2 island region in the collisionless simulations with and without the RMP.On the low field side,the electron diamagnetic frequency is only slightly affected by the RMP, which is consistent with the change of density profile on the low field side.On the high field side, the electron diamagnetic frequency is significantly changed across the 8/2 island region, because the density profile is flattened locally.

Figure 5.Electron density profiles ne (panel a) and diamagnetic frequency ωe* profiles (panel b) in rigid rotation case in 8/2 island region in collisionless simulations after profile relaxation.Reddotted and black solid lines are profiles on low field side and high field side with RMP.Blue-dashed line is profile without RMP.Vertical dashed lines represent island separatrices.

3.2.Simulation with the experimental equilibrium profiles

We now use experimentalneandTeprofiles described in section 2.3.Two sets of simulations are carried out with or without the RMP.The first set uses the experimentalneprofile and a uniformTe=Te(q=4) ,thuskt= 0.The second set uses both the experimentalneandTeprofiles as the equilibrium profiles.

Figure 6 shows the steady stateΓeprofiles in the simulations.In the simulations without the RMP,the ambipolarΓein the case with experimentalTe(kt>0) is slightly smaller than that in the uniformTe(kt=0) case, which qualitatively agrees with the standard neoclassical theory [48].In the simulations with the RMP,both uniformTeand experimentalTeproflies can induce the non-ambipolar particle fluxesΔΓe.We rewrite the non-ambipolar particle flux ΔΓe=D0(kn+βkt),whereD0is the transport coefficient in the uniformTe(kt=0)case, β denotes the ratio between the contribution from temperature and density gradients.We find thatβ= 0.56,which is qualitatively consistent with the NTV theory [13].

The neoclassical simulations use the RMP equilibrium calculated by the M3D-C1, which could have a large uncertainty in the magnetic island width.Therefore, we perform a sensitivity study for the RMP amplitude α.Figure 7 shows the dependence ofΔΓeon the α on theq=4 surface from GTC neoclassical simulations using experimental equilibrium profiles, where α0is the original RMP amplitude calculated by the M3D-C1.It is clear thatΔΓefollows a quadratic relation with α, i.e.the non-ambipolar flux is proportional to the magnetic island width.

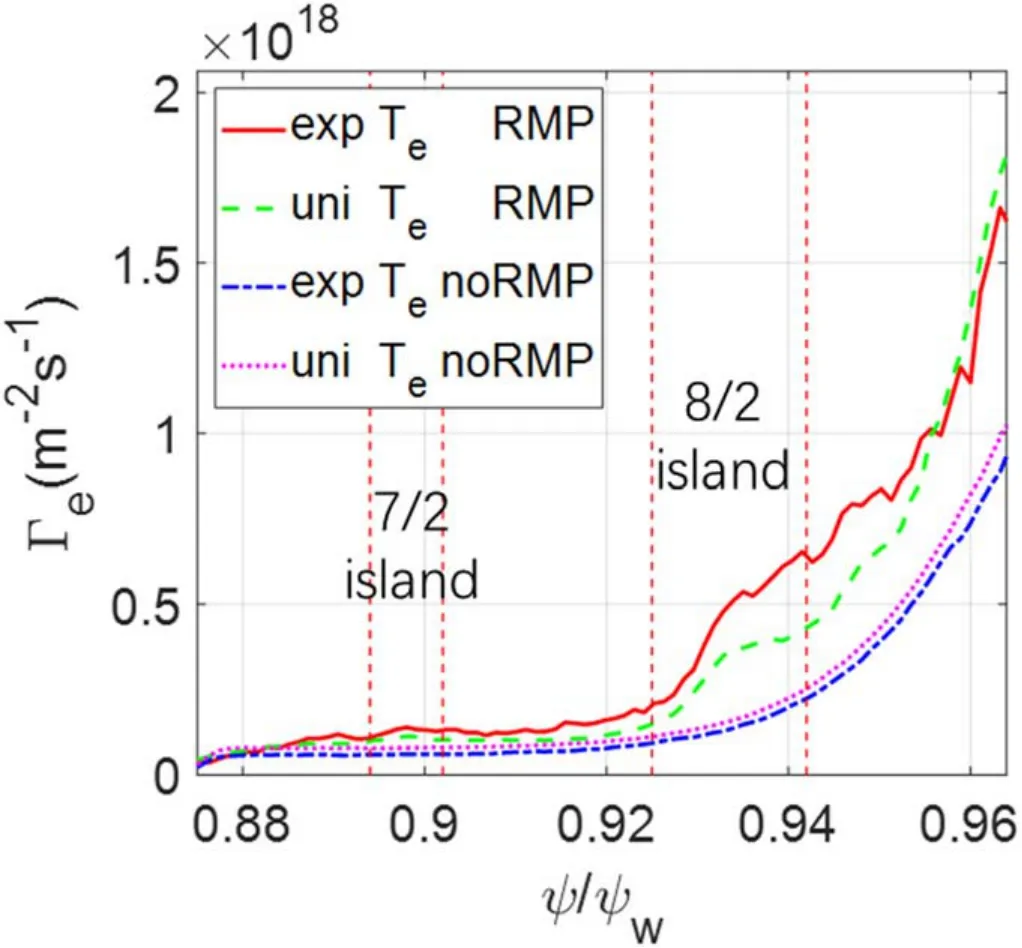
Figure 6.Electron particle fluxΓe profiles from neoclassical simulations using experimental density profile,experimental Te(lines with ‘exp’ label) or uniform Te profiles (lines with ‘uni’ label), with and without RMP (lines with ‘RMP’ and ‘noRMP’ label).Vertical dashed lines represent island separatrices.

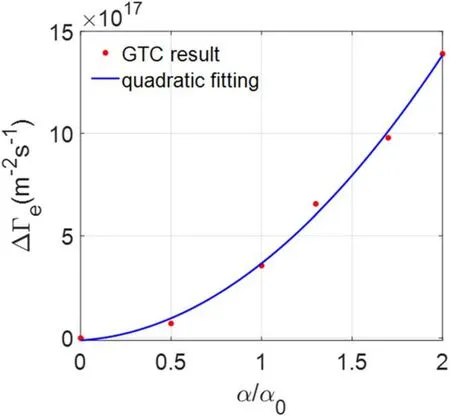
Figure 7.Dependence of non-ambipolar electron particle flux ΔΓe( q =4)on RMP amplitude α from neoclassical simulation.The blue line is a quadratic fti.

4.Effect of RMP on neoclassical particle flux with equilibrium electric field

In this section, the effects of equilibrium electric fieldEron the neoclassical transport is studied.During the time scale of the ELM suppression (∼1 ms), the equilibrium density and temperature profiles do not change much,but the equilibrium electric fieldErcan change significantly,which can affect the neoclassical and turbulent transport [11, 31].

Figure 8(a) shows the radial profiles of the experimental equilibriumEron the outer midplane during the ELMing(3796 ms) and ELM suppression (3050 ms) in the DIII-D discharge #158103.In this section, these twoErprofiles,together with theneandTeprofiles at 3050 ms,are used as the equilibrium.The 8/2 island width is much smaller than the typical equilibrium inhomogeneity scale length,which allows us to use the 1D equilibrium electric field.

First,we verify the effects of the equilibrium electric fieldErusing the uniformknandTeprofiles with the value at theq=4 flux surface.Uniformprofiles (rigid rotation case) or experimentalErprofiles are used in the simulations separately.Figure 8(b) shows theΔΓenear the =q4 surface at the steady state of neoclassical simulations using the equilibrium with the RMP and the uniform electric fieldEψ.Here,we useEN≡to represent the amplitude of the electric field, which corresponds to the ratio between the E×B and diamagnetic flows.TheENvalues of 2.9 and−0.22 correspond to the local value of the electric field during the ELMing and the ELM suppression, respectively.The value ofEN= −1corresponds to the toroidal rotation frequency Ωte= 0.In the rigid rotation case, whenEN= −1,theΔΓeis three orders of magnitude smaller than the neoclassical particle flux without the effect of RMP.When theEN≠−1,the absolute value of theΔΓebegins to increase,which can change the radial electric field and damp the rotation,in qualitative agreement with the neoclassical theory[48, 49] predicting the toroidal flow damping by the toroidal viscosity due to the 3D magnetic fields.

In the simulations using the experimentalErprofiles without the RMP,the shear of the equilibrium electric fieldErhas little effects on theΓe,because the electrons banana orbit width is much smaller than the radial scale length of the electric field.In the simulations with the RMP, both the experimentalErprofiles during the ELMing and the ELM suppression are found to induce additional positiveΔΓewhen compared with the uniform electric field.The value ofΔΓein the simulation with theErduring the ELMing is much larger than that during the ELM suppression, which indicates that the rotation damping during the ELMing is much larger than that during the ELM suppression.

Finally,to compare with the experimental measurements of rotation damping, we carry out simulations using the experimentalne,Te,and the twoErprofiles.Figure 8(c)shows theΓeprofiles at the steady state of these neoclassical simulations with or without the RMP.In the simulations without the RMP, the shear ofErhas little effects on theΓe,same as the simulation results in the rigid rotation case.In the simulations with the RMP, theErprofile during the ELMing induces a much larger non-ambipolar particle fluxΔΓethan that during the ELM suppression.This indicates that the nonambipolar particle fluxΔΓecan drop drastically during the ELM suppression,which is mainly due to the rapid change of the equilibrium electric fieldEr.The sensitivity of the electron flux on the equilibrium electric field indicates that some electron orbits become stochastic due to the RMP.

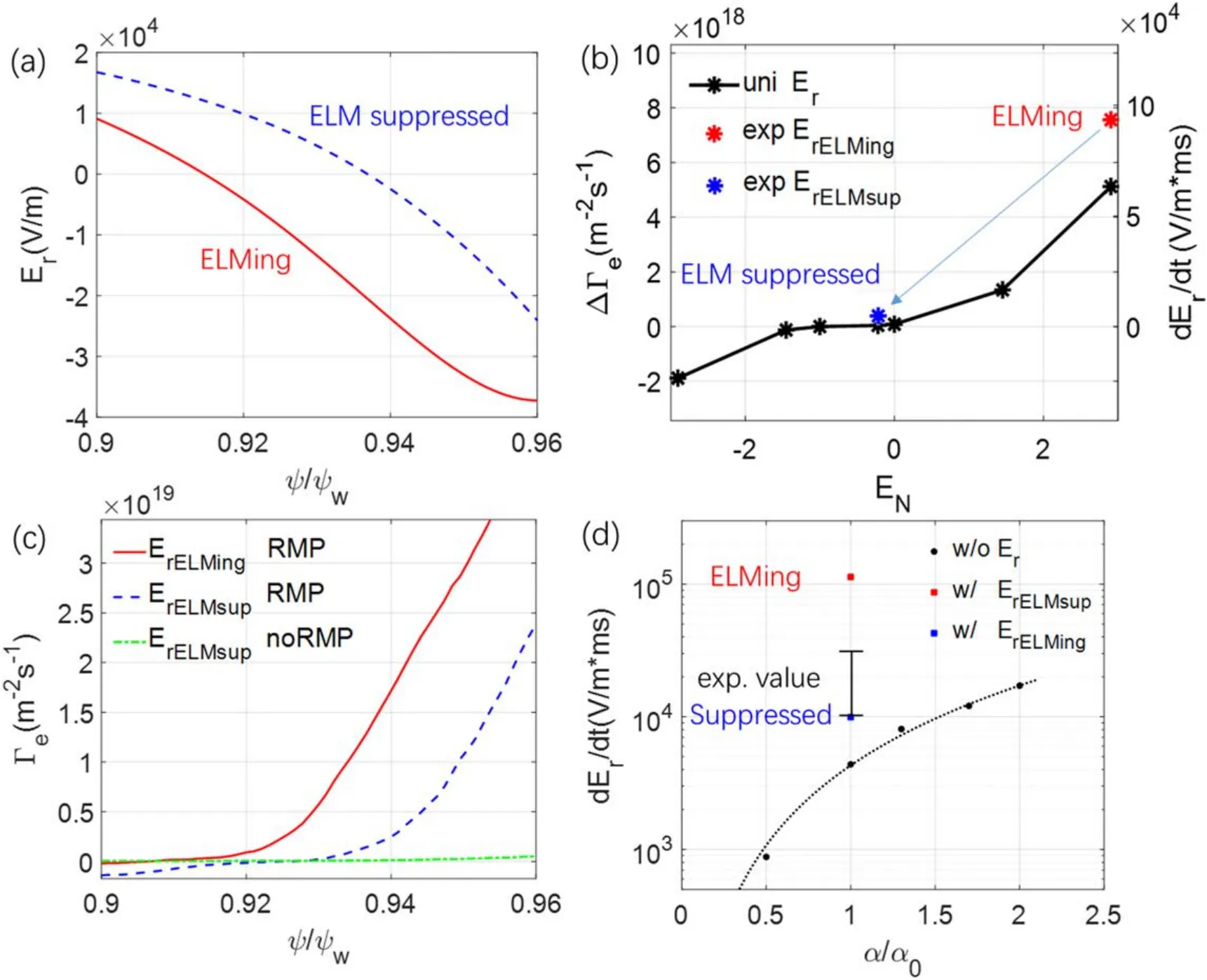
Figure 8.(a)Equilibrium electric field Er profiles of DIII-D for#158103 discharge during ELMing and ELM suppression.(b)Dependence of non-ambipolar particle flux ΔΓe on electric field amplitude EN at =q 4 flux surface in simulations with uniform and experimental Er profiles,using the uniform kn and Te profiles.(c)Profiles ofΓe at steady state of neoclassical simulations with Er profiles during ELMing(blue line)and ELM suppression(red line),and without RMP(yellow line),using experimental density and temperature profiles.(d)Dependence of time rate of change of Er at =q 4 flux surface on RMP amplitude α from simulations without equilibrium Er and with equilibrium Er during ELMing and ELM suppression.Error bar represents experimental value with 50% uncertainty range.

5.Rotation damping rate due to non-ambipolar particle flux

In this section, we calculate the damping rate of the toroidal rotation by calculating the time rate of change of the electric fieldErusing the non-ambipolar particle fluxΔΓemeasured in the steady state of the neoclassical simulations in the previous sections.Combining the gyrokinetic Poisson’s equation and guiding center continuity equation, the quasi-neutrality condition takes the form [50],

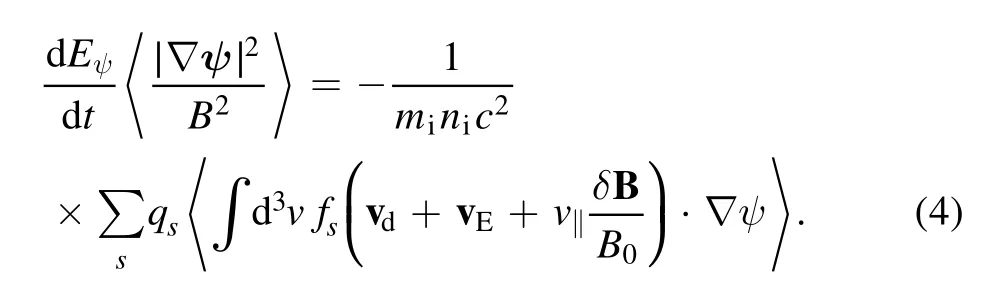
Here,the subscriptsdenotes the particle species(i for ion and e for electron).The flux-surface-averaged polarization current on the left hand side cancels out with the guiding center current on the right hand side.The relation betweenand radial electric fieldErisTheΓiandΓeare assumed to be ambipolar without the effects of RMP.For the non-ambipolar particle fluxes,only the electron contribution is taken into account by assuming that the ion contribution is negligible.Equation (4) is then used to calculate the damping rate of the toroidal rotation.

Figure 8(d) shows the damping rate at theq=4 fulx surface calculated from the simulations using the experimentalne,Teand the two experimentalErprofiles plotted in figure 8(a).When comparing simulation results with the experimental measurement of the damping rate during the ELM suppression,two aspects of uncertainty should be considered.The first one comes from the MHD simulations of the RMP amplitude α.In the α amplitude scanning,the damping rate is about one third of the experimental level whenα=α0,but reaches the experimental level when usingα= 2α0.The second uncertainty comes from the rapid change of theErduring the transition from ELMing to ELM suppression.The damping rate is proportional to the non-ambipolar particle fulxesΔΓe,which depends on theEramplitude and shear, as shown in fgiure 8(b).From the ELMing and ELM suppression state, the damping rate decreases drastically due to the change of the equilibrium electric feilds.This result is consistent with the experiment, in which the toroidal rotation experiences a large torque before the onset of the ELM suppression,followed by relatively small torque after the transition to the ELM suppression state.The simulated damping rate during the ELM suppression qualitatively agrees with the experimental value.

6.Effects of RMP on collisionless damping of zonal flows

To understand the RMP effects on zonal flow dynamics,collisionless zonal flow damping and GAM are simulated by using two types of the 3D RMP fields.Besides the RMP equilibrium described above, another equilibrium is obtained from the ideal MHD code VMEC [29, 51], which includes only the non-resonant response of the RMP and thus preserves the closed flux surfaces.For the VMEC equilibrium,an electrostatic version of the fluid-kinetic hybrid electron model[52] is used to treat the kinetic electrons.In this model, the perturbed electron distribution function is represented byis the adiabatic response to the non-zonal electric field, andδheis the nonadiabatic response.For the M3D-C1 equilibrium with magnetic islands, the drift kinetic equation DKE [40] is used for solving the electron perturbed distribution function.Both the zonal and nonzonal electric field components are solved together in the presence of magnetic islands.The ion dynamics is simulated by solving the standard gyrokinetic equation.The radial particle flux in this section is defined as

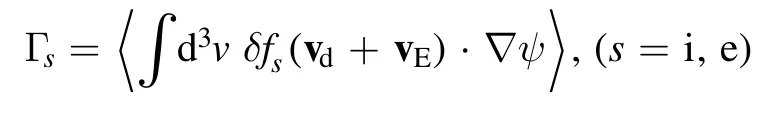
for the ions and electrons in the hybrid model using the VMEC equilibrium, and

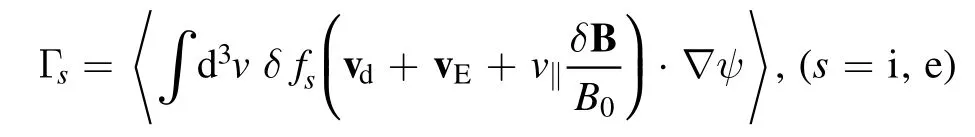
for the ions and the electrons in the DKE model using the M3D-C1 equilibrium.

In these simulations, a flux-surface-averaged ion guiding center density perturbation is initiated to generate the zonal flows.The radial profile of the zonal flows is set to be a sinfunction with a radial wavevectorkrρi=0.4.The density perturbation is set to be zero at the inner and outer boundaries of the simulation domainψ= [0.90, 0.97]ψw.Simulations in this section use uniform equilibrium density and temperature profiles for both ions and electrons (Ti≈1.7Te), corresponding to the local parameters at the =q4 surface of the DIII-D experiment.

Firstly, we study effects of kinetic electrons by using gyrokinetic ions and fluid-kinetic hybrid electron model[52].The time evolution of the radial electric fieldErof the zonal flows on the =q4 surface using the VMEC equilibrium with various RMP amplitudes(without RMP,or amplified by 1,2,5,10 times)are shown in the figure 9(a).We can see that the radial electric field evolves with a finite frequency, i.e.damped GAM oscillation, and then reaches a steady state.In the simulation without the RMP,the zonal flow residual level is very close to that in the simulation only with the adiabatic electrons, which indicates that the effect of the kinetic electrons in zonal flow damping could be neglected without the RMP.The zonal flow residual level is much higher than the Rosenbluth–Hinton theory [53], which neglects shaping effect and finite aspect ratio.

In the simulations with different RMP amplitudes, the change of the residual flowΔEris defined as the difference between theErand that in the simulation without the RMP at the same simulation time.TheΔEris found to depend quadratically on the RMP amplitude,which is consistent with that in the section 3.3.As shown in the figure 9(b),when the RMP amplitude is amplified by 10 times, the change of the residual flowcould reach 60%, which is three times larger than that in the simulation with only the adiabatic electrons.Here, theR0is the major radius at magnetic axis,is the speed of ion acoustic wave.

Figures 9(c) and (d) show the time history of radial particle fluxes for the ionΓiand electronΓein simulations without RMP and RMP×10.TheΓioscillates with the GAM frequency beforet=10R0/cs.Subsequently, theΓigradually drops to a much lower level in both the simulations.On the other hand, theΓehas a strong oscillation with the GAM frequency beforet=10R0/cs,which is mainly due to electrons adiabatic response to the non-zonal electric fields(m≠0,n=0), through the product ofδfe(0)withvd.TheΓestays at a high level duringt=(10 −35)R0/csin the simulation with RMP×10, but is always very small aftert=12R0/csin the simulation without the RMP.This indicates that electron orbits could become stochastic due to the large RMP amplitude, and the residual flow damping is mainly induced by electrons,rather than ions.This result may have implications on zonal flow dynamics in the tokamaks with ripple fields and in the stellarators.

Figure 9.In simulations using VMEC equilibrium with closed flux surfaces, time evolutions of radial electric field Er of zonal flow with kinetic electrons with various RMP amplitudes (panel a), (b) relation between change of residual flow ΔEr at t=50 R 0/cs and RMP amplitude α,radial particle flux(arbitrary unit)of ionΓi (panel c)and electronΓe (panel d)during zonal flow damping process without RMP(dashed lines)and with RMP×10(solid lines).Er is normalized with initial value,ΔEr is normalized with residual flow without RMP,and particle flux is normalized with value ofΓe at t=10R0/cs in simulation with RMP×10.

Finally,to study the effects of the RMP islands on zonal flow damping, the M3D-C1 equilibrium is used.The time evolutions of the radial electric fieldErof the zonal flows with various RMP amplitudes (without RMP, with RMP and RMP×2) are shown in the figure 10(a).In the simulation without the RMP,the residual zonal flow is close to the result of the VMEC equilibrium within a difference of 20%, which could be due to the differences in the equilibrium and simulation model.The GAM oscillation (during (0–5)R0/cs) is strongly damped when the RMP amplitude increases.The residual flow in the simulation with the RMP×2 amplitude with the magnetic islands has a 30%reduction,which is much larger than that in the simulation using the VMEC equilibrium without magnetic islands.

Figure 10(b)shows the ion and electron particle fluxes in simulations without RMP and with RMP×2 using the M3DC1 equilibrium with magnetic islands.In the simulation without the RMP, the electron particle fluxΓeoscillation is strong during the GAM oscillation.In the simulation with RMP×2,the electron particle fluxΓechanges strongly at the early time (<2 R0/cs), which is mainly due to the magnetic flutter effect from the fast parallel motion of the elections.The GAM oscillation is then strongly damped by this radial transport.The radial secular drifts of electrons due to stochastic orbits or helically trapped electrons lead to adiabatic electron response to zonal flow, which damps GAM and reduces zonal flow residue level.

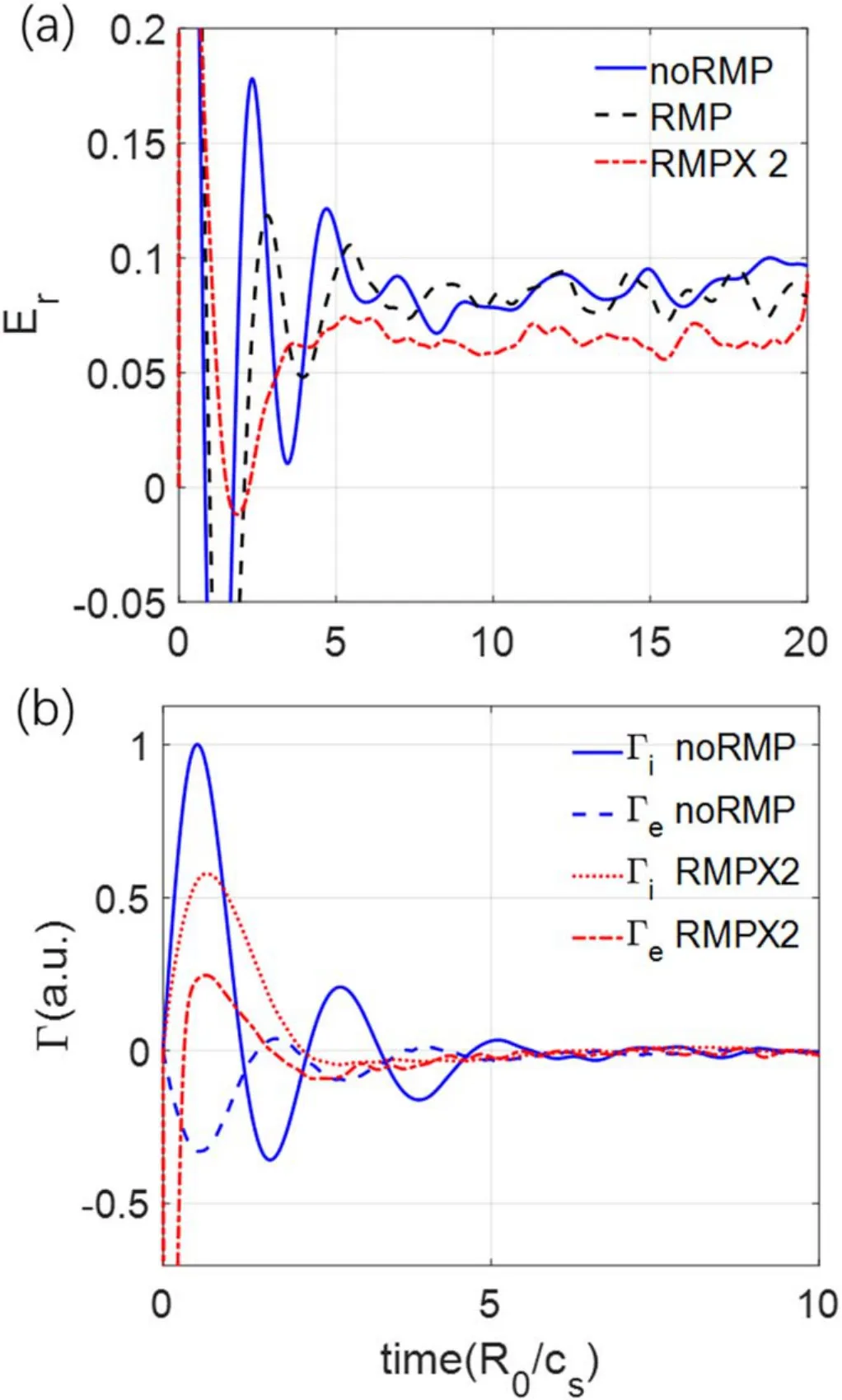
Figure 10.Time evolutions of radial electric fieldEr of zonal flows(panel a), ion and electron radial particle fluxes (panel b), with various RMP amplitudes in simulations using M3D-C1 equilibrium including magnetic islands. Er is normalized with initial value,particle fluxes are normalized with maximal value of ion particle flux Γi in simulation without RMP.

7.Conclusion and discussion

In this paper, we use GTC simulations to study the RMP effects on radial electric fields, including both equilibrium electric fields associated with toroidal rotation and zonal flows.The GTC simulations use realistic DIII-D tokamak equilibrium with both resonant and non-resonant responses to 3D RMP calculated by resistive MHD code M3D-C1.Neoclassical simulations show that the 3D RMP-induced magnetic islands and stochastic electron orbits can drive nonambipolar electron particle fluxes, which lead to a rapid change of equilibrium radial electric field,consistent with the experimental observations during the transition from ELMing to ELM suppression state.The GTC neoclassical simulation results provide a support for the conjecture that the RMPinduced change of radial electric fields leads to enhanced turbulent transport at the pedestal top during ELM suppression.Furthermore,GTC simulations of collisionless damping of zonal flows find that resonant response to the RMP can decrease the residual level and damp the GAM.

Most of our simulation results for the pedestal top (i.e.RMP effects on edge Er,plasma flows,and GAMs)during the ELM suppression are very similar to those observed in earlier Ohmic experiments in Tore Supra [54], TEXTOR [55], and MAST [56], where the modelling using vacuum RMP field predicts the stochastic magnetic fields in the pedestal region.Nonetheless, there are important differences in the effects on plasma transport between the stochastic magnetic field in the pedestal region and the strongly screened magnetic perturbation on the pedestal top.The neoclassical transport in the stochastic magnetic field could dominate over the turbulent transport, while the turbulent transport dominates in the strongly screened magnetic perturbation because of a weakerErshear induced by the non-ambipolar neoclassical transport(see the figure 7 in [31]).

In future simulations, we will couple tokamak core with SOL including magnetic separatrix, which could incorporate ion orbit loss near the separatrix.We will also develop the coupled neoclassical and turbulence simulations.Furthermore, the transport of RMP-induced energetic particles will also be studied by GTC.

Acknowledgments

The authors would like to thank J Bao, L Shi and S Taimourzadeh for useful discussion, and acknowledge technical support by the GTC team.This work was supported by the China National Magnetic Confinement Fusion Science Program(Nos.2017YFE0301300 and 2018YFE0304100);by the US Department of Energy (DOE) grant DE-SC0020413 and SciDAC ISEP Center, and by Princeton Plasma Physics Laboratory under Contract DE-AC02-09CH11466.This work used the resources of the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory(DOE Contract No.DE-AC05-00OR22725) and the National Energy Research Scientific Computing Center (DOE Contract No.DE-AC02-05CH11231).The work used data from the DIII-D National Fusion Facility, a DOE Office of Science user facility, under Awards DE-FC02-04ER54698.DIII-D data shown in this paper can be obtained in digital format by following the links at https://fusion.gat.com/global/D3D_DMP.

This paper was prepared as an account of work sponsored by an agency of the United States Government.Neither the United States Government nor any agency thereof,nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy,completeness, or usefulness of any information, apparatus,product,or process disclosed,or represents that its use would not infringe privately owned rights.Reference herein to any specific commercial product,process,or service by trade name,trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof.The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.

ORCID iDs